一个定理及其推广在异面直线距离问题中的应用

杨德国

摘 要：求异面直线距离的方法比较多，有些方法运算量较大，而有些方法技巧性较强.文章将各种各样的异面直线距离问题归结为两类模型，先研究模型，得到定理及其推广，然后利用定理及其推广，可以快速解决很多的异面直线距离问题.

关键词：异面直线；距离；定理；推广；应用

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2024）13-0080-03

异面直线的距离是立体几何中的一个难点.2019年人教B版普通高中教科书《数学选择性必修第一册》35页的例题4就是一道考查异面直线距离的习题.由此可见，课本比较重视异面直线的距离问题.

那么，如何求解异面直线的距离呢？对于这个问题，已经有不少文献做了研究，总结起来主要的方法有：定义法（即找共垂线）、函数法（即求一直线上的点到另一直线的距离的最小值或者两直线上的动点的距离的最小值）、转化法（即转化为点线距、线面距或面面距）、向量法（即求出两异面直线的公垂线的方向向量，然后利用投影向量求解）和射影法等[1-3].

是否可以把各种各样的异面直线距离问题归结为某类模型，然后利用模型去快速解题呢？笔者经过探究，得到了如下的一个定理，并将其进行推广.

1 与异面直线距离有关的一个定理

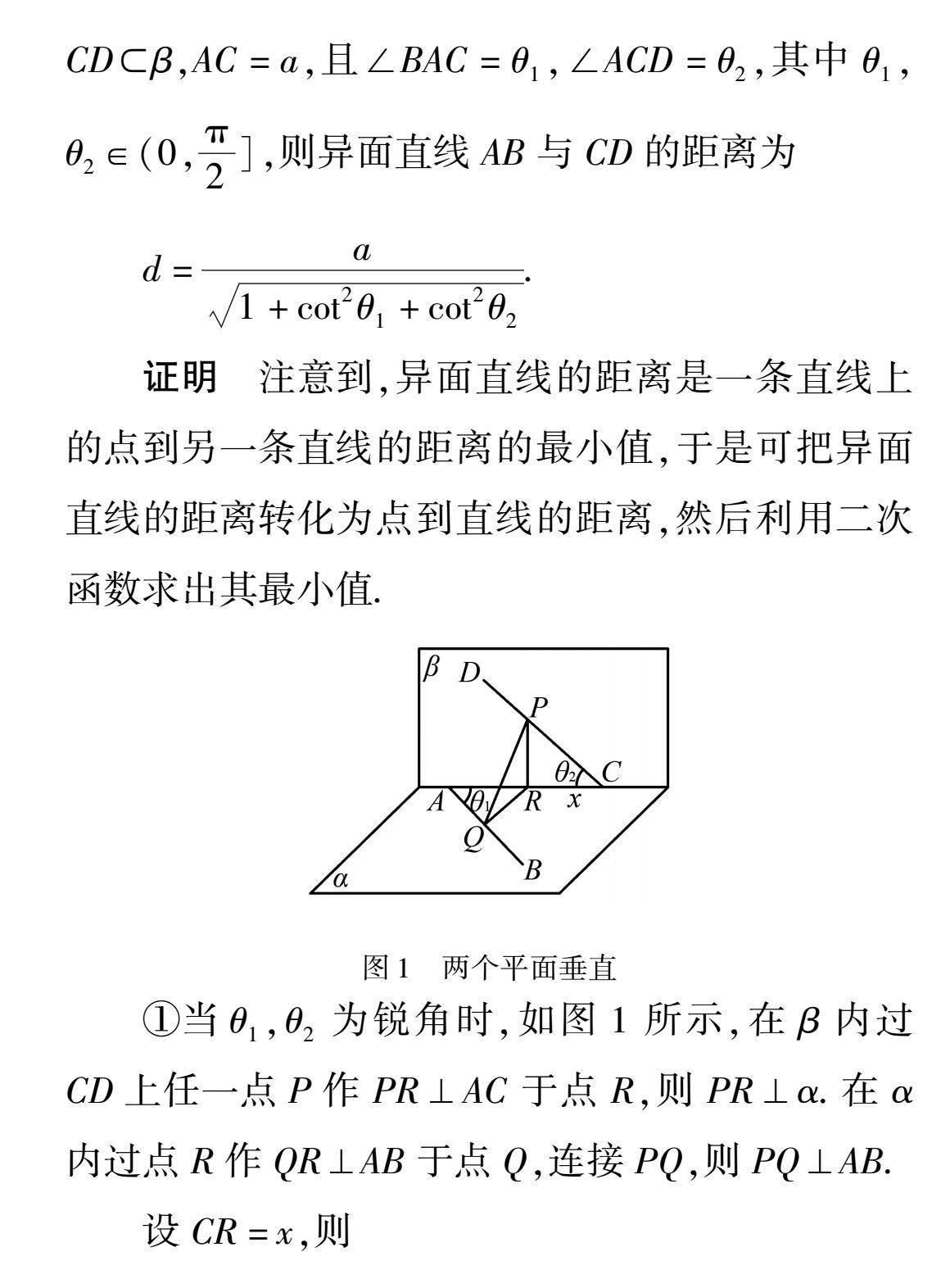
定理1[4] 在直二面角α-AC-β中，ABα，CDβ，AC=a，且∠BAC=θ1，∠ACD=θ2，其中θ1，θ2∈（0，π2］，则异面直线AB与CD的距离为

d=a1+cot2θ1+cot2θ2.

证明 注意到，异面直线的距离是一条直线上的点到另一条直线的距离的最小值，于是可把异面直线的距离转化为点到直线的距离，然后利用二次函数求出其最小值.

①当θ1，θ2为锐角时，如图1所示，在β内过CD上任一点P作PR⊥AC于点R，则PR⊥α.在α内过点R作QR⊥AB于点Q，连接PQ，则PQ⊥AB.

设CR=x，则

AR=a-x，PR=xtanθ2，QR=（a-x）sinθ1.

所以PQ2=x2tan2θ2+（a-x）2sin2θ1=（tan2θ2+sin2θ1）x2-2axsin2θ1+a2sin2θ1.

所以当x=asin2θ1tan2θ2+sin2θ1时，

PQ2min=a2tan2θ2·sin2θ1tan2θ2+sin2θ1=a2csc2θ1+cot2θ2

=a21+cot2θ1+cot2θ2.

所以异面直线AB与CD的距离为

d=PQmin=a1+cot2θ1+cot2θ2.

②当θ1为锐角，θ2=π2时，CD⊥α.

过点C作CQ⊥AB于点Q，则有CD⊥CQ.

所以CQ就是异面直线AB与CD的距离.

此时d=CQ=asinθ1.

经检验，当θ2=π2时，cotθ2=0，此时

d=a1+cot2θ1+cot2θ2=a1+cot2θ1=asinθ1.

综合①②知，当θ1为锐角，θ2∈（0，π2］时，定理1的公式都成立.

注 当θ2为锐角，θ1∈（0，π2］时，定理1的公式仍然成立.而当θ2=0时，CD∥α，问题可转化为直线CD到平面α的距离，进而可转化为直线CD上一点到平面α的距离.这是极为容易求解的，在此不作讨论.

如果二面角α-AC-β不是直二面角，那么怎么求异面直线AB与CD的距离呢？为了解决这个更一般性的问题，我们给出定理1的推广.

定理2 已知二面角α-AC-β的大小为锐角φ，ABα，CDβ，AC=a，且∠BAC=θ1，∠ACD=θ2，其中θ1，θ2∈（0，π2］，则异面直线AB与CD的距离为

d=asinφsin2φ+cot2θ1+cot2θ2+2cotθ1cotθ2cosφ.

一般地，给定的两条异面直线，其基本符合定理1或定理2的模型，因此可以利用定理1或定理2快速解决异面直线的距离问题.下面举例说明.

2 定理的应用

例1 已知正方体ABCD-A1B1C1D1的棱长为a，求异面直线A1B与B1D1的距离.

解析 如图2所示，A1B平面ABB1A1，B1D1平面A1B1C1D1，且平面ABB1A1⊥平面A1B1C1D1，∠BA1B1=45°，∠D1B1A1=45°.

根据定理1可得异面直线A1B与B1D1的距离为

d=a1+cot245°+cot245°=33a.

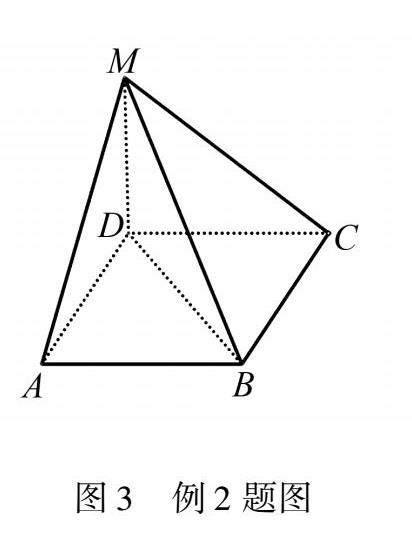
例2 在四棱锥M-ABCD中，底面ABCD是边长为a的菱形，且MD⊥底面ABCD，MD=a2，∠BAD=60°，求异面直线MA与BD之间的距离.

解析 如图3所示，MA平面MAD，BD平面ABCD，因为MD⊥底面ABCD，所以平面MAD⊥平面ABCD.

因为四边形ABCD是菱形且∠BAD=60°，

所以∠BDA=60°.

设MAD=θ，则cotθ=ADMD=2.

根据定理1可得异面直线MA与BD的距离为

d=a1+cot260°+cot2θ=a1+1/3+4=34a.

例3 已知三棱锥S-ABC的底面是边长为42的正三角形，SC=2，且SC⊥底面ABC.设D，E分别为AB，BC的中点，求异面直线CD与SE的距离.

解析 如图4，因为SC⊥底面ABC，SC平面SBC，所以平面SBC⊥底面ABC.

又因为D，E分别为AB，BC的中点，可得

cotθ1=cot∠DCB=cot30°=3，

cotθ2=cot∠SEC=CESC=2.

根据定理1可得异面直线CD与SE的距离为

d=CE1+cot2θ1+cot2θ2=221+3+2=233.

例4 已知正方体ABCD-A1B1C1D1的棱长为a，E，F分别为棱BC，AB的中点，求异面直线D1E与DF的距离[5].

解析 如图5所示，DF平面ABCD，D1E平面A1BCD1，因为A1B⊥BC，AB⊥BC，所以二面角A1-BC-A的大小为φ=∠A1BA=45°.

易知四边形A1BCD1为矩形.

所以cotθ1=cot∠D1EC=ECD1C=24.

又AD∥BC，所以cotθ2=cot∠FDA=DADF=2.

根据定理2得，异面直线D1E与DF的距离为

d=asinφsin2φ+cot2θ1+cot2θ2+2cotθ1cotθ2cosφ

=2a/21/2+1/8+4+2×（2/4）×2×（2/2）

=25a5.

3 结束语

异面直线的距离问题，试题多样，变化万千，但它们基本上都可以归结为定理1或定理2的模型.定理1的模型就是两条异面直线所在的平面互相垂直，所以直棱柱中的很多异面直线问题都可归结为定理1的模型.定理2的模型是两条异面直线所在的平面不是互相垂直，但两个平面的夹角是易求的.很多的异面直线难题都可归结到定理2的模型.

与其教给学生一题多解，还不如教会学生多题一解.让学生学会思考，学会把各种各样的试题经过分析整理后，归结到一类或者两类模型.只需把这一类或者两类模型研究透了，各种试题自然就迎刃而解了.这样，教师不仅在无形中落实了“双减”政策，学生的学习能力和数学学科核心素养也得到了提升.

参考文献：

［1］ 邹明.用向量方法求空间角和距离[J].数学通报，2004（05）：36-38.

[2] 李家琪.求异面直线距离的一种方法：射影法[J].数学通报，1984（06）：19-21.

[3] 张传伟，丁振年.异面直线距离的一种简便解法[J].数学通报，2004（05）：35-36.

[4] 赵强.异面直线距离的求法[J].中学数学教学参考，2017（10）：41-43.

[5] 李鸿昌.点在面内的多视角证明与高观点审视：一道2020年立体几何高考题引发的探究[J].数理化解题研究，2023（22）：101-104.

［责任编辑：李 璟］