高中数学教学活动中STEAM理念的应用策略

STEAM教育理念以激发兴趣爱好为切入点，鼓励学生在学习中自主探究，寻找解决策略，提高综合能力。本文研究如何将STEAM素养融入高中数学教学实践，本质上是整合高中数学的学科知识，使整个学习过程变得立体、有层次——以学科学习为主要内容，从知识、技能、情商、智力、价值观等渗透点向外无限辐射。教师依据本区域的教学现状，从学生的能力、兴趣、关注点出发设计教学过程，激发学生的自主学习能力，促进学生在学习过程中发挥主观能动性，进而培养学生的数学核心素养。

一、高中数学教学活动与STEAM理念融合过程分析

本节课是探讨空间直线与平面之间关系的起点，其中蕴含了众多深刻的数学思想，如将空间问题转化为平面问题，或者将无限问题转化为有限问题等。这些思想为后续学习面与面之间的平行关系，以及线与面之间的垂直关系提供了必要的理论知识和方法论基础。

传统教学忽视了学生“发现过程”的重要性，导致学生在学习过程中只会生搬硬套，无法灵活运用定理解决问题，因此教师将STEAM理念融入教学势在必行。为了深化学生的实践操作技能，激发他们的创新思维，笔者精心设计了以“折纸艺术”为核心的探究活动。这些活动将工程技术（S）的核心理念融入其中，有效锻炼学生的空间想象能力，提升其数学建模素养。此外，笔者将艺术（A）与数学理念相融合，在思辨环节着重提升学生的逻辑推理能力。

二、高中数学教学活动中STEAM理念应用分析

（一）教学目标

1.明确如何判断直线与平面呈平行关系（判定定理）并灵活应用，利用艺术、工程等理念实现学科融合。

2.通过折纸试验明晰定理的由来过程，提升空间想象力和逻辑思维能力。

3.在折纸的过程中学会将立体几何问题转化为平面问题，掌握转化能力，体会化归思想。

（二）设计理念

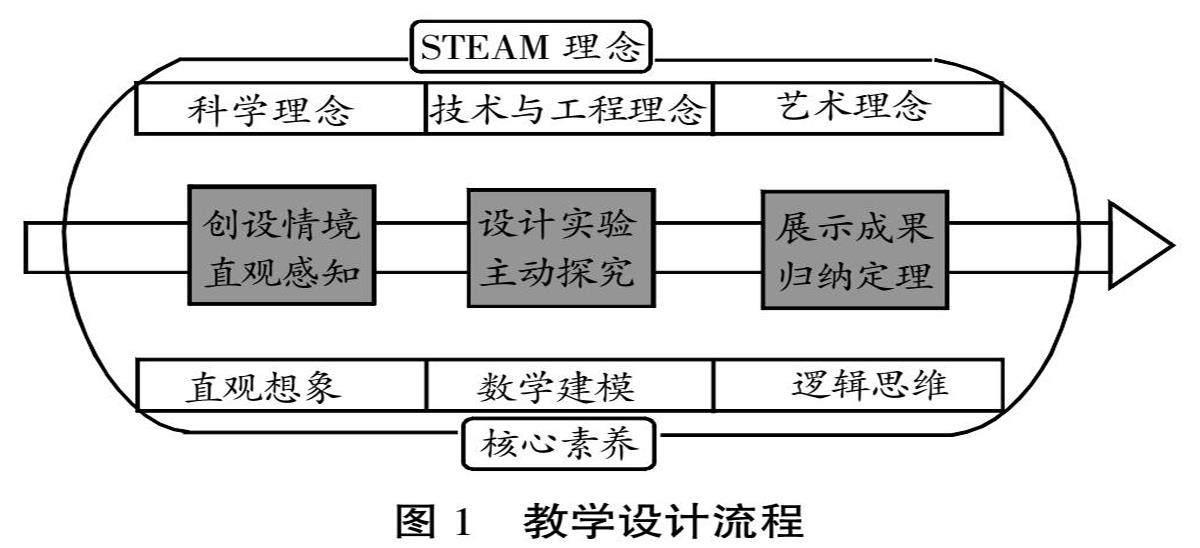
在本次课程的设计中，笔者精心构建了三个主要环节（如图1所示），旨在引领学生经历一场知识内化的过程。这一设计不仅揭示了直线与平面平行判定定理的探索过程，还激励学生自主探索，独立完成知识体系的构建。在此过程中，学生能够提升自身的数学建模能力，强化自己的空间想象力、逻辑推理等数学核心素养。

（三）教学过程

任务一：通过生活事例激发空间感知能力

教师：在三维空间中，直线与平面之间存在哪些可能的位置关系？

学生：二者平行、二者相交、一条直线在平面上。

教师：在日常生活中，我们能找到哪些例子，让我们直观地感受到线面平行的概念呢？

学生：例如，教室里的日光灯棒与地面，或是足球门框上沿所在的直线与操场地面，都是线面的平行现象。

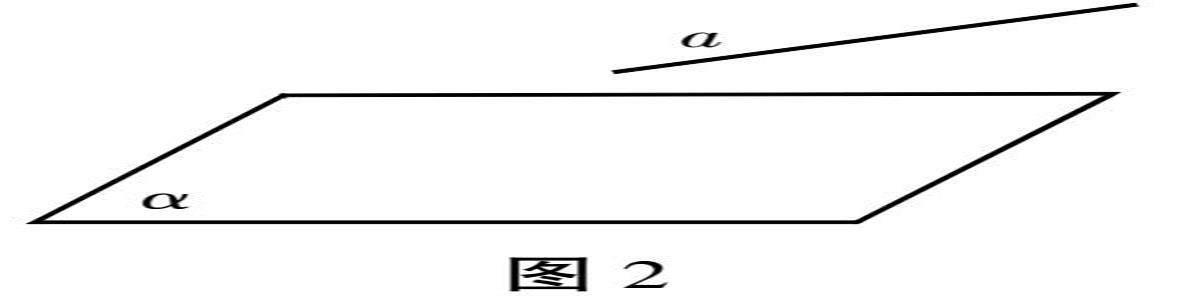
教师：那么，我们如何去判定一条直线是否与一个平面平行呢？（用多媒体展示图2），让我们来观察直线a与平面α的关系。直线a是否与平面α平行？请阐述你的观点和理由。

学生1：不平行，它俩虽然现在没相交，但是将直线延长之后肯定会和平面相交的。

学生2：通过肉眼观察没办法判定它们俩是不是平行的，万一是角度造成的错位呢？

（设计意图：当前学生已经掌握了直线与平面平行的基本概念：两者无公共点，但是图2引发了激烈的讨论，学生意识到直接观察无法验证图形之间的关系，因为直线与平面都是无限延伸的。这种认知上的矛盾促使学生认识到学习本节课的重要性，为知识体系的构建奠定了坚实的基础。）

任务二：设计实验，带动主动探究

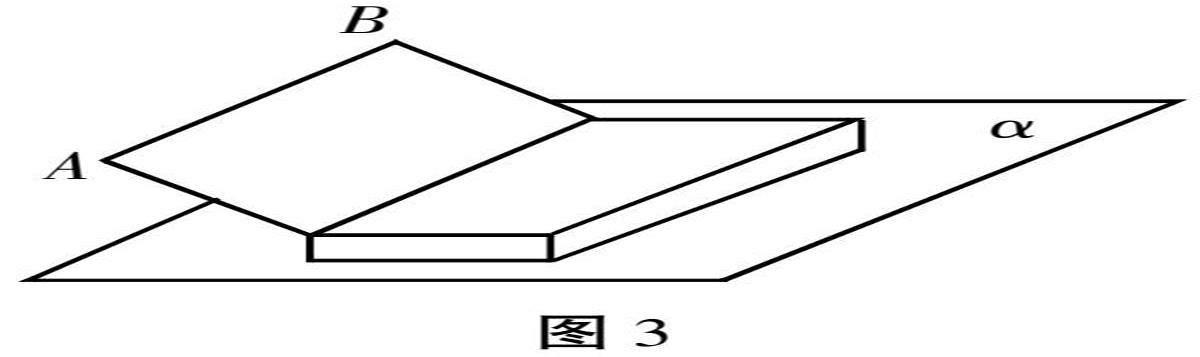
（用多媒体展示图3）

教师：请仔细观察屏幕上的图片。你们感觉线段AB与平面α是什么关系？

学生：如果单纯用眼睛看的话好像是平行的，但我不敢确定。

教师：没错，从数学角度来说，图形之间的关系必须通过一系列证明才能得出结论，那么我们现在共同做一个小实验，来验证一下这条线和平面是否平行。

实验指导：现在请大家拿出我们准备好的卡纸，将这张纸的四个点标注为A点、B点、C点和D点，接下来把这张卡纸平放在桌面上，现在我们以立体几何的角度来观察桌面，将桌面标注为平面α。接下来，请你们动动手，随便折一下这张纸，随后在折痕的两端标记上点E、F。

教师：现在请大家以小组的形式探究两组问题：

（1）在我们的这张纸上线段CD是否与折痕EF平行呢？线段CD与平面α是否平行呢？如果是，请说明原因。

（2）折叠能让线段CD与平面α平行吗？具体原因是什么呢？

（学生小组讨论，教师巡视）

教师选取两组学生进行示范。

（设计意图：折纸实验是数学思想与技术理念的融合，引导学生学会建立模型分析问题，培养学生运用抽象思维解决实际问题的能力。此外，小组合作的形式使学生能够在交流和讨论中互相学习、共同进步，有效丰富学生的学习生活，为他们未来的人生道路奠定坚实的基础。）

任务三：展示成果，总结归纳定理

学生（小组代表）：我们观察到折痕EF与CD不平行时，四边形CDEF便呈现出梯形的形状。在这样的情况下，梯形的两条腰DC和EF如果被延长，它们必定会在某一点上相交。假设这个交点是M，那么点M就会位于直线EF上。由此，我们可以推断出点M同样位于平面α内，这表明直线CD与平面α发生了相交（如图4所示）。

教师：你们小组完成得非常棒，接下来我要找一个小组回答第二个问题，我们该怎样让CD与平面α保持平行呢？说出具体操作方法和原因。

学生（小组代表二）：折痕EF与CD保持平行时就意味着直线CD与平面α之间存在平行关系，具体原因我也解释不清楚……

教师：没关系，这也是我们本节课学习的重点，接下来我们一起探讨一下。

教师：判定线段CD平行于平面α的依据是什么？

学生：我们之前学的平面和直线存在平行关系的定义。

教师：要精确地定义直线CD与平面α的平行关系，我们必须确定它们之间不存在任何交点。换句话说，平面α上的任意一点都不会位于直线CD上。

（学生举手表示要进行详细说明）

学生：这张纸上的折痕也就是EF与CD是平行关系，也就是说这两条线不会产生交点，换句话说，折痕EF也不会和平面α内的任何一点相交，这个时候我们在平面α上做一条与EF平行的线，只要证明该平行线和CD平行，就能证明EF平行于CD了。

教师：你说的完全正确，在探讨直线与平面平行的条件时，我们可以依据定义来阐述这一概念。那么你能根据定义总结一下什么情况下直线与平面平行吗？

学生：直线和平面在三维空间中没有任何公共点，即直线上的任何一点都不在平面内，直线与平面没有任何交点，也就是说，直线完全位于平面的另一侧。如果直线上的两点都在平面外，那么过这两点的直线与平面平行。

（设计意图：折纸实验的引入，不仅丰富了教学手段，更让学生在动手操作中直观地理解了线面平行的条件，为后续几何学的学习打下了坚实的基础。）

三、高中数学教学活动中STEAM理念应用实践思考

（一）立足STEAM理念制订教学目标

过去，教师经常将精力集中于单独学科的知识和能力传授，这种做法过于强调结果的重要性，忽视了学习过程的价值，无法通过课堂教学促进学生发散思维，更遑论培养其创新能力。相比之下，STEAM教育理念则提倡多学科的深度融合，突出跨学科知识和技能的综合运用。教师若能立足于STEAM理念，教学目标的设定将更加全面且精确，促使高中数学课堂从单纯的知识技能传递转变为学生能力和素养的提升。通过这种转变，学生能迅速掌握必要的知识，同时发展其理论知识的综合应用能力和创新精神，为未来的学习和生活打下坚实的基础。

（二）依据STEAM理念设计探究活动

在STEAM教育理念中，动手操作结合思维活动是其核心特征之一。在上述教学内容中，学生面临的主要挑战是掌握教材中涉及的“降维”概念，就是将空间中线面平行的复杂问题转化为更为简单的线线平行问题，需要具备一定的空间想象力。本节课通过折纸、自主探究等实践活动将抽象的空间形式具体化、形象化，从而在学生的大脑中形成清晰的空间印象。学生通过亲手制作模型，不仅能直观地观察到空间形式的转换，还能将复杂问题简单化，亲历探究数学问题的完整流程。从知识的发现到生成，每一个步骤都锻炼了学生的思维能力。在这个过程中，学生不仅学习了教材中的知识，更重要的是体会到了其中所蕴含的思想方法，并揭示了数学知识的理性思维和教育价值，为未来的学习和生活打下坚实的基础。

（三）运用STEAM理念提升学生素养

在STEAM教育理念指导下，小组合作成为课堂学习的基石，带动学生展开自主探究式学习。在探索直线与平面平行性的过程中，学生与教师互动频繁，共同探讨问题，思想的火花在讨论中不断迸发，不同的观点相互碰撞，充分调动了自身的主观能动性。在实践中动手操作和深入反思论证中，学生逐渐掌握发现问题并解决问题的技能，如将复杂问题简化、空间问题平面化等，从而有效地增强了在模型建立、空间想象和思辨推理等领域的素养。STEAM教育理念视域下的教学并不是对传统教学方法的彻底摒弃，而是学科融合基础上的教育升华。在这种融合教学模式中，立体几何的教学超越了简单的知识传授，转而以学生的主动探索为活动中心，通过知识的传授与拓展来构建课程，清晰地体现了STEAM教育探究性和开放性的特点，进而全面提升学生的综合能力。

（作者单位：甘肃省庆阳市庆城县驿马中学）

编辑：陈鲜艳

作者简介：刘俊琴（1971—），女，汉族，甘肃庆城人，本科，高级教师，研究方向：中学数学教育教学。