数字化赋能下的高中数学探究式教学实践

李玲

探究式教学是数学新课标中提出的一项新的教学模式，它重视学生的主体地位，注重师生之间的互动，在数字化赋能模式下其优势更为明显，能为学生带来更加丰富的学习体验。本文借助数字化教育技术工具开展“圆与圆的位置关系”教学，旨在让学生主动探究，学会学习。

一、教材分析

“圆与圆的位置关系”是人教A版（2019）选择性必修第一册第二章“直线和圆的方程”中的内容，是学习直线和圆的方程中最为基础和重要的部分。圆与圆的位置关系是点与圆、直线与圆的位置关系的延伸，是学生学习几何知识和解析几何的重要基础。

二、数字化赋能下探究教学的意义

教师通过数字化信息技术工具实现高中数学探究教学实践，不仅可以培养学生的数学兴趣，促进学生数学建模能力的发展，而且可以促进学生信息素养的培养。引入数字化高中数学智能课程可以为学生带来具体的、实用的学习体验，吸引学生主动参与数学探究活动。所以，数字化赋能下的高中数学探究教学可以很好地满足当代高中生的学习发展需要，有助于学生主动探索数学知识并掌握课堂知识。

三、教学过程

（一）创设情境，导入新课

1.动画情境，激趣引入

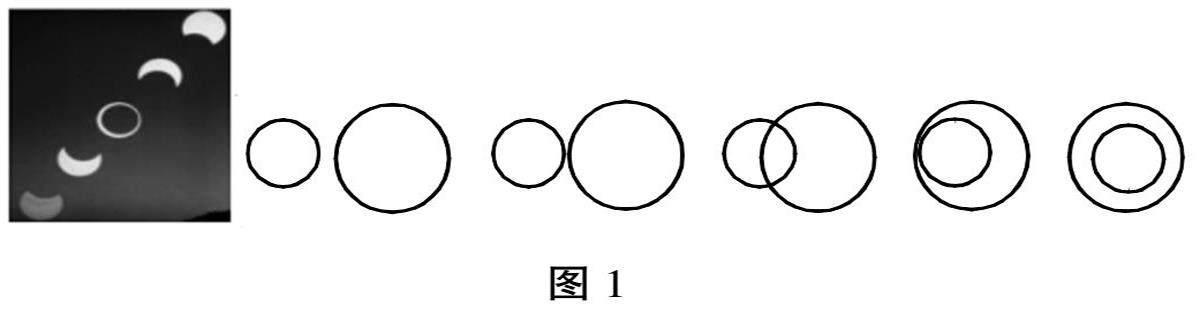
师：同学们，大家都知道日环食吧。现在，如果我们从数学的角度把太阳和月亮看作是两个圆，那么通过月亮和太阳的运动，就形成了两个圆与圆的位置关系。

（通过微视频呈现日环食的全过程，以及圆与圆的位置关系图形，如图1所示。）

（设计意图：用日环食这一天文现象激发学生对新知主动探索的兴趣。用数字化短视频将日环食图文并茂地呈现在学生面前，可以触发学生的视觉感受，再通过情境的转化导入新知，这样学习效果更佳。）

2.逐层演示，揭示概念

师：大家仔细观察微视频中两个圆运动变化产生的位置关系。

（正常速度播放微视频）

生1：两个圆慢慢靠近但还没有接触之前，它们属于外离关系。

生2：当圆与圆接触，它们只有一个交点时，这两个圆属于外切关系。

生3：当两个圆有两个交点时，这两个圆属于相交关系。

生4：当小圆彻底融入大圆，有且只有一个交点时，两圆关系属于内切。

生5：当小圆彻底融入大圆中且没有交点时，两圆内含。

师：大家看一下两个圆运动时的动作回放。

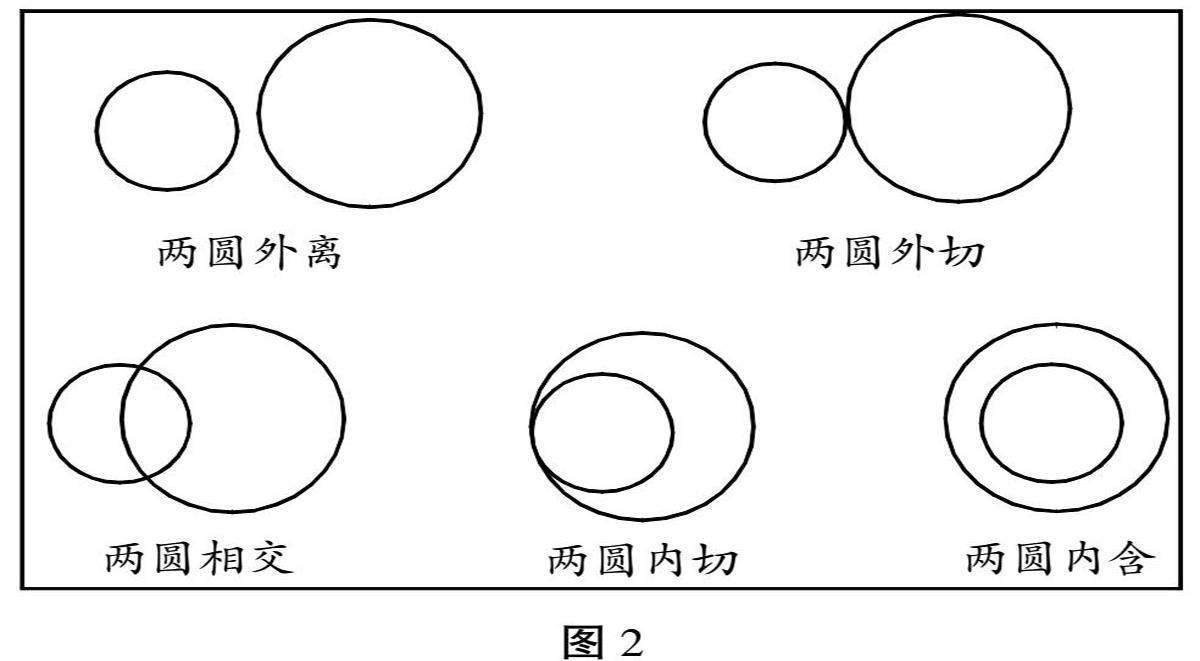
（用微视频慢播放呈现五种位置关系，如图2所示。）

（设计意图：通过微视频让学生进行自主观察、探索并得出圆与圆的五种位置关系、五种位置关系的特点性质，让学生逐步构建知识体系。）■

图2

（二）探究本质，得出新知

探究一：圆与圆位置关系的判定

师：通过前面的学习，我们如何判定圆与圆的位置关系是外离、外切、相交、内切、内含呢？

生1：观察两个圆之间是否有交点，如果没有交点，那就是外离或者内含；如果有交点，那就是外切、相交或内切。

师：外离、内含该如何判定？外切、相交、内切又该如何判定？我们能否通过数量关系来判断位置关系呢？

生2：我们可以通过两个圆的圆心距和半径来判定。如果圆心距大于两个圆的半径之和，那么两圆外离；如果圆心距等于两个圆的半径之和，那么两圆外切；如果圆心距小于两圆半径之和那么两圆相交、内切或内含。

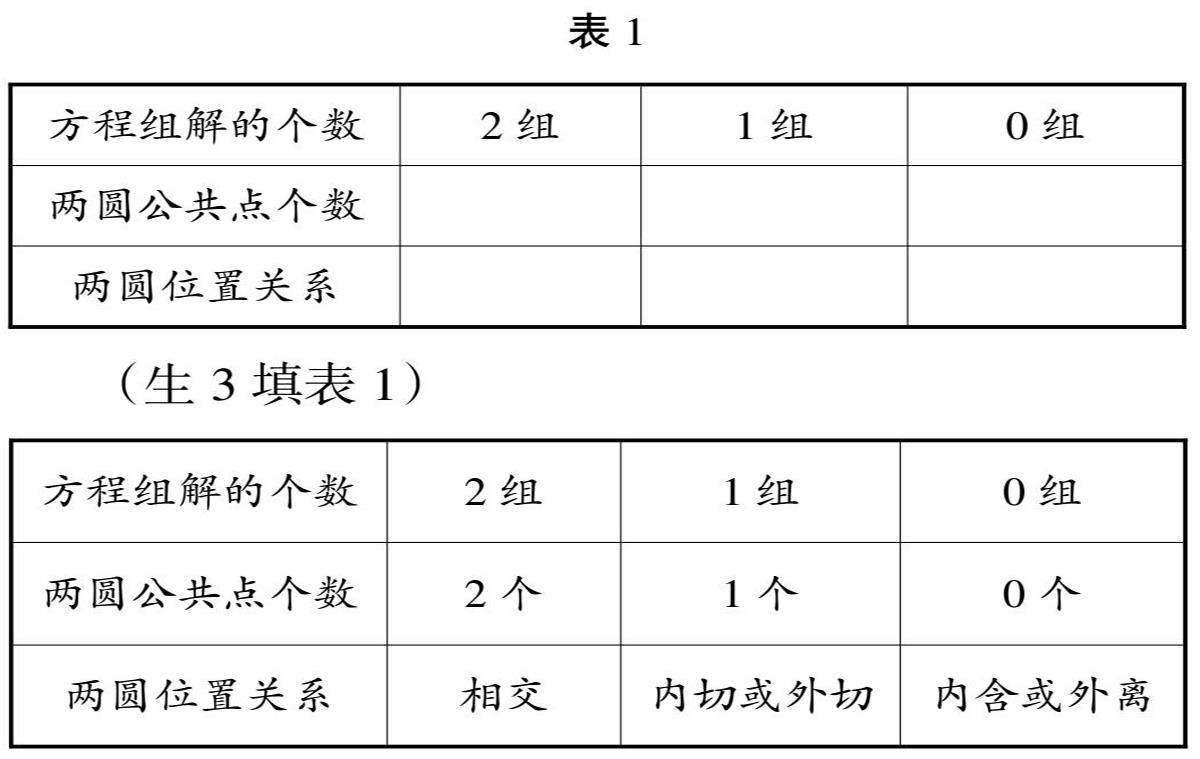
师：那么又出现了一个新的问题，圆心距小于半径之和时又该怎样判断两圆是相交、内切还是内含呢？下面我们一起探索影响圆与圆位置关系的数量因素。出示用代数的方法来判断圆与圆的位置关系的图表（见表1）：

师：假设两个圆C1和C2的半径分别为r1、r2，圆心距为d，那么两个圆的位置关系如表2所示。

（设计意图：通过教师提问学生探究，教师再提问学生再探究的方式，激发学生主动探究的积极性。学生在探究过程中发现问题、分析问题、解决问题并获得自主学习能力的提升。）

探究二：习题训练，强化巩固

师：将两个相交的圆的方程x2+y2+Dix+Eix+Fi=0（i=1，2）相减，可以得到一条直线方程，那么这条直线方程具有什么特殊性？

生：两圆相减得到一条直线方程，那么它会经过两个圆的交点，所以该直线为两圆公共弦所在的直线。

（设计意图：通过练习题拓展学生思维，让学生转换思维，形成举一反三的能力，达到学以致用的目的。）

（三）内化巩固，拓展探究

1.判一判

师：圆是轴对称图形，那么两个圆共同组成的图形也是轴对称图形吗？

生1：是的，它们的对称轴就是两个圆圆心的连线。

师：经过两个圆心的线称为连心线，两个圆心间线段的长度为圆心距。

师：如果两个圆相切，那么切点与连接线的位置关系如何？

（让学生画一画）

生2：切点会在这条连接线上。

师：非常正确，所以我们得到了“如果两圆相切，那么切点一定在连心线上”这一数学性质。

（设计意图：学生通过判断、动手、动脑获得正确答案，这样既可以锻炼学生自主解决问题的能力，又可以提高学生的逻辑思维能力。）

2.玩一玩

教师设计课堂游戏竞赛，将班组学生分成若干小组，每小组由两人组成，各成员要相互配合，确定所得答案的正确性及解题过程及步骤的规范性。分组时采用“帮带”原则，按照“组内异质，组间同质”分配小组，保证每个小组都能水平相当、能力相近、公平竞争。

具体设计如下：先用多媒体呈现例题，得到例题之后每个小组有5分钟的时间来解答，解答完成之后直接让学生提交。计算机通过大数据处理对提交的答案给予判定。哪一组提交的答案既快又准确，给哪一组加一分。一共设置例题5道，满分5分，用时25分钟。

（设计意图：一是通过例题对课堂所讲知识进行强化和巩固；二是借助数字化信息技术工具组织课堂游戏，让课堂变得生动有趣；三是通过科学合理分组探究，帮助全班学生共同进步。）

3.练一练

师：前面我们学习了两圆不相等情况下的位置关系，如果两圆半径相等，两个圆的位置关系会有几种？

生1：（学生自主画图）四种：外离、外切、相交、重合，因为两圆半径相同时它们内切和内含时会重合。

（教师用多媒体进行动画展示）

（设计意图：让学生触类旁通，用常规方法解决个别问题。）

师：如果两圆是内含关系，两圆的圆心在同一个位置上（圆心重合），那么圆心距为多少？

生2：圆心距为0。

（多媒体展示图形）

（设计意图：设计这种探究类问题，主要是为了让学生掌握特殊情况下的特殊条件，避免出现忽视条件而结题的错误。）

师：如果两个圆的半径为5+t和5-t（0＜t＜5），圆心距为2t，那么两圆的位置关系是怎样的？

生3：如果圆心距为2t，那么2t=（5+t）-（5-t），所以两圆为内切关系。

（设计意图：从已知圆心距来求两个圆的位置关系，用反向思维来推断确定位置关系，解题效率更快。）

师：两圆外切时圆心距为12，内切时圆心距为4，求这两个圆的半径分别为多少。

生4：假设两个圆的半径分别为r1、r2则：

外切时圆心距为r1+r2=12.............A

内切时圆心距为r1-r2=4................B

A+B=2r1=16，所以，r1=8，r2=4.

因此，这两个圆的半径分别为8和4。

（设计意图：如果学生的思维只停留在前两部分，那么将很难得到解。这一练习题型的设计不仅是对前两个题型的巩固和延伸，还是对学生思维转化能力的锻炼。）

（四）课堂总结，完善认识

本节课我们学习了圆与圆的五种位置关系，以及每个位置关系的判定方式，借助数字化信息技术工具组织了一系列课堂探究活动；并对通过相应的数量关系来判定圆与圆的位置关系，做了一些较为基础的练习题，旨在加强学生对本节基础知识的掌握，为以后的学习奠定了基础。

四、教学反思

优点：本课以深度学习为理论基础，以现代信息技术工具为课堂辅助，以问题为导向，以学生自主探究为主要方式，注重在实践中应用、在应用中强化，构建了数字化赋能下的高效高中数学课堂教学设计，让学生能在“真实”的学习情境中通过自主探究、合作探究等方式深入了解了圆与圆的位置关系，并能运用理论知识解决实际问题。

不足：在课时设计上留给学生自主探究和发现的时间太少。为减轻学生课后学习的压力，教师应充分利用好数字化工具，以提高课堂教学容量和效率，给学生更多的课余时间去完成一些具有探索性的数学学习任务。

（作者单位：山西省太原市晋阳街山西省实验中学）

编辑：蔚慧敏