基于二阶滑模扰动观测的PMSM电流预测控制研究

林立　胡俊　谭乐　李亚楠　王翔

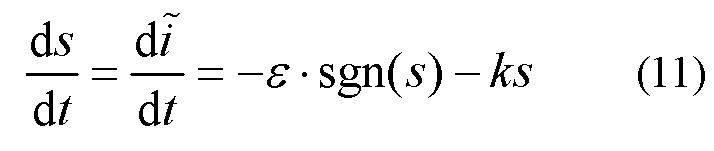
摘要：针对无差拍电流预测控制（DPCC）对电机参数的依赖性，系统性能尤其易受电感参数影响的问题，研究基于二阶滑模扰动观测的永磁同步电机（PMSM）电流预测控制方法。首先，根据滑模控制原理分析电感参数失配对系统参数鲁棒性的影响，及传统滑模控制的不连续函数导致的系统“抖振”；然后，在DPCC中引入一种基于二阶趋近律的滑模扰动观测器（SMDO），实时补偿电感参数失配造成的扰动，同时通过二阶趋近律加速扰动误差的收敛；最后，将该方法与DPCC、SMDO+DPCC进行对比仿真实验。实验结果表明，在电感参数失配的情况下，该方法降低了电流稳态误差，提高了系统参数的鲁棒性，减少了传统滑模控制带来的系统“抖振”现象。

关键词：永磁同步电机；无差拍电流预测控制；滑模控制；二阶趋近律；滑模扰动观测器

中图分类号：TM341             文献标志码：A          文章编号：1674-2605（2024）03-0004-10

DOI：10.3969/j.issn.1674-2605.2024.03.004

Research on PMSM Current Predictive Control Based on Second-order       Sliding Mode Disturbance Observation

Abstract： To address the issue of the dependence of DPCC on motor parameters and the susceptibility of system performance to inductance parameters， a permanent magnet synchronous motor （PMSM） current prediction control method based on second-order sliding mode disturbance observation is studied. Firstly， based on the principle of sliding mode control， the impact of inductance parameter mismatch on the robustness of system parameters is analyzed， as well as the system "chattering" caused by discontinuous functions in traditional sliding mode control; Then， a sliding mode disturbance observer （SMDO） based on second-order convergence law is introduced in DPCC to compensate for disturbances caused by inductance parameter mismatch in real time， while accelerating the convergence of disturbance errors through second-order convergence law; Finally， compare the method with DPCC and SMDO+DPCC through simulation experiments. The experimental results show that in the case of mismatched inductance parameters， this method reduces the steady-state error of current， improves the robustness of system parameters， and reduces the system "chattering" phenomenon caused by traditional sliding mode control.

Keywords： permanent magnet synchronous motor （PMSM）; deadbeat predictive current control （DPCC）; sliding mode control; second-order convergence law; sliding mode disturbance observer

0  引言

永磁同步电机（permanent magnet synchronous motor， PMSM）具有功率密度高、运行速度范围广、节能环保等特点，广泛应用于工业机器人控制等领域[1]。在PMSM的经典控制中，电流环作为电机的控制内环，其性能影响输出转矩的响应速度，而输出转矩的响应速度直接决定了电机的响应速度、负载能力等性能。为了提高工业机器人控制系统的性能，研究具有较强鲁棒性的电流环控制策略非常必要[2-3]。

无差拍电流预测控制（deadbeat prediction current control， DPCC）根据PMSM模型预测控制电压，实现了无差拍电流跟踪，具有动态性能好、计算量小、电流波纹小等特点[4-5]。但其系统参数鲁棒性不高，依赖参数模型，PMSM参数尤其是电感参数与控制器参数失配会导致电流稳态误差、系统发散等问题，影响控制性能。针对该问题，专家学者们提出了许多改进方法，主要分为扰动观测器[6-8]、参数辨识法[9-10]、鲁棒控制算法3类[11-13]。其中，扰动观测器结构简单，在保证系统性能的同时降低了电感参数失配的影响；参数辨识法虽然可以计算出PMSM的实际参数，但计算量较大，且易受外部干扰；鲁棒控制算法虽能减小电感参数失配造成的稳态误差，但未能充分发挥DPCC动态性能好的优势。

为此，本文研究基于二阶滑模扰动观测的PMSM电流预测控制方法。通过在DPCC中引入二阶滑模扰动观测器（sliding mode disturbance observer， SMDO），对电感参数失配的扰动进行实时补偿，有效减小了电流稳态误差，抑制了滑模控制中出现的“抖振”现象。

1 DPCC

1.1 PMSM数学模型

PMSM控制系统采用id = 0的矢量控制，其在同步旋转d-q坐标系下的电压方程为

式中：ud、uq、id、iq分别为d、q轴的定子电压和电流，Ld、Lq分别为d、q轴的定子电感，R为定子电阻，Ψf为转子永磁体磁链，ωe为转子电角速度。

在表贴式的PMSM中，d、q轴的电感分量相等Ld = Lq，公式（1）可转化为

1.2DPCC原理

DPCC的目标是能够对下一拍的电流进行预测。将公式（2）转换为交直轴电流状态方程，并采用前向欧拉法离散化，得到离散PMSM方程为

为了使PMSM电流在k+1时刻跟随给定值，需要知道实际控制器中相应的控制电压。

若公式（3）中的PMSM参数均为实际参数，将PMSM在k时刻计算的交直轴电流作为下一时刻的电流：

可求解k时刻的控制电压，使PMSM电流在下一时刻能够跟随给定值：

式中： 为PMSM的实际参数。

由公式（5）可知，DPCC在PMSM实际参数模型下，能够计算出控制电压。但在实际应用中，PMSM参数会随温度发生改变，与控制器参数不匹配。此外，在离散系统中不可避免地存在延时，k时刻的控制电压，在实际运行时转子旋转了一个角度，导致稳态电流跟踪出现误差。

2 二阶趋近律的SMDO设计

2.1 SMDO

当PMSM实际参数偏离控制器参数时，PMSM在d-q坐标系下的电压方程为

式中： ， ， ， 为控制器的模型参数。

SMDO设计为

将公式（6）与（8）作差，得到d、q轴的误差方程为

根据滑模控制理论，SMDO的设计可分为滑模面函数和滑模控制函数两部分。传统的滑模控制选用指数趋近律来设计滑模面函数：

对滑模面函数求导，得到

式中：ε参数控制趋近速度，k参数控制调节时间，均为实数。

将公式（11）代入公式（9），可得到滑模控制函数表达式：

经过离散化处理，SMDO可表示为

2.2 SMDO稳定性分析

为满足SMDO的稳定性条件，使电流估计误差

根据李雅普诺夫稳定性条件：

为使系统渐进稳定，参数ε的范围为

建立参数扰动估计值的一阶方程：

求解，得到

由公式（19）可知，当参数ε > 0时，系统满足稳定性条件，交直轴电流误差的估计值能够收敛至0，系统能够在有限的时间内到达滑模面，SMDO是渐进稳定的。

SMDO离散结构框图如图1所示。

利用SMDO中k+1时刻的预测电流代替k时刻的采样电流，可解决DPCC的延时问题，减小电流跟踪误差。

2.3 二阶趋近律的SMDO

传统滑模控制采用指数趋近律，通过参数ε和k调节滑模变结构的运动模态，但其控制律是不连续函数，导致系统易出现“抖振”现象。为解决该问题，本文采用一种由幂次趋近律和等速趋近律组成的二阶滑模趋近律算法，将控制器中的不连续项代入控制输入的二阶滑模趋近律中，经过积分，控制输入变为连续，可有效抑制系统的“抖振”。

式中：k1、k2为稳定增益参数，可调节系统的稳定性，抑制“抖振”；k3为收敛增益参数，可调节系统的收敛速度。

当|s|<1时，系统状态趋近滑动模态，幂次趋近律保证系统具有较小的控制增益，减小“抖振”；当|s|>1时，等速趋近律保证系统能快速准确地到达滑模面，抑制系统“抖振”。将二阶趋近律公式（18）代入误差方程公式（9），可得到二阶滑模控制函数表达式：

2.4 二阶趋近律的SMDO稳定性分析

稳定的。同样，当参数满足稳定性条件时，SMDO离散形式如公式（17）所示。二阶趋近律的SMDO离散结构如图2所示。

式中： 和 为经参数扰动补偿后的定子电压，DPCC输出的预测电压 和 为

3 仿真结果分析

3.1 系统动态性能仿真

本文基于Simulink仿真平台验证基于二阶滑模扰动观测的PMSM电流预测控制方法的动态性能，并与PI控制进行对比分析。PMSM参数如表1所示。

仿真测试中，直流母线电压为200 V，逆变器开关频率为10 kHz，仿真时长为0.5 s，电机给定转速为   1 000 r/min，在0.25 s时增加负载转矩10 N·m。

本文方法与PI控制转速响应如图3所示。

由图3可知：当采用本文方法驱动PMSM启动时，相较于PI控制，能够更快地跟踪给定转速，超调小于2%，进入稳定状态后没有静差；在0.25 s增加负载时，系统的转速变化较小，相较于PI控制，能够更快地恢复对给定值的跟踪，表明本文方法在控制系统中表现出较好的动态性能和抗干扰能力。

3.2 模型参数失配的性能仿真

为验证本文方法（二阶趋近律的SMDO+DPCC）的参数鲁棒性，将其与DPCC及SMDO+DPCC进行仿真比较。在电感参数失配，其他参数与标称值一致的情况下，3种控制方法的d、q轴电流响应如图4、5所示。

由图4可以看出：当PMSM实际电感参数为控制器电感参数的0.6倍时，图4（a）施加负载稳定后，d、q轴电流稳态误差分别为0.041、0.112 A；图4（b）经过SMDO补偿后，d、q轴电流稳态误差分别为0.004、0.039 A，但d轴电流幅值波动为1.6 A；图4（c）采用二阶趋近律的SMDO后，d、q轴电流稳态误差分别为0.002、0.030 A，d轴电流幅值波动减小至0.19 A，有效减少了传统滑模控制的“抖振”现象；同时d、q轴电流波形毛刺明显减少，说明基于二阶趋近律的SMDO具有较好的补偿效果。

由图5可知：当PMSM实际电感参数是控制器电感参数的2倍时，图5（a）在施加负载稳定后，d、q轴电流稳态误差分别为0.897、0.080 A；图5（b）经过SMDO补偿后，d、q轴电流稳态误差分别为0.038、0.054 A，电流稳态误差减小，但d轴电流的振荡较大，上下波动为2.2 A；图5（c）采用二阶趋近律的SMDO后，d、q轴电流稳态误差分别为0.029、0.073 A，d轴电流振荡减小，上下波动为0.2 A，有效抑制了传统滑模控制的固有“抖振”现象，具有良好的控制效果，表明本文方法提高了控制系统的参数鲁棒性。

电感参数失配时，DPCC与二阶趋近律的SMDO+DPCC的电流稳态误差对比如表2所示，SMDO+DPCC与二阶趋近律的SMDO+DPCC的电流振幅对比如表3所示。

由表2、表3可知：在电感参数失配时，相较于DPCC，二阶趋近律的SMDO+DPCC的d轴电流误差减小率分别为95.12%和96.76%，具有较好的参数鲁棒性；相较于SMDO+DPCC，二阶趋近律的SMDO+ DPCC的d轴电流振幅抑制率分别为88.13%和90.91%，“抖振”抑制效果明显。

4 结论

针对电机电感参数失配时，DPCC受限于PMSM模型参数，产生电流稳态误差的问题，根据滑模控制原理，引入二阶趋近律的SMDO对DPCC进行改进。改进后的二阶趋近律的SMDO+DPCC，通过实时补偿减小了电流稳态误差，同时抑制了传统滑模控制的高频“抖振”现象。仿真结果表明，二阶趋近律的SMDO+DPCC在动态性能和抗干扰能力方面具有良好的控制效果，在PMSM实际电感参数是控制器电感参数的0.6和2倍时，PMSM的d轴电流稳态误差减小率分别为95.12%和96.76%，振幅抑制率分别为88.13%和90.91%，减小了电感参数失配引起的电流稳态误差，解决了传统滑模控制的“抖振”现象，进而提高了系统参数的鲁棒性。

参考文献

[1]    林立，秦芳清，陈玮，等.工业机器人伺服控制系统建模及仿真[J].邵阳学院学报（自然科学版），2019，16（6）：25-32.

[2]    王恩德，黄声华.表贴式永磁同步电机伺服系统电流环设计[J].中国电机工程学报，2012，32（33）：82-88;179.

[3]    牛里，杨明，王庚，等.基于无差拍控制的永磁同步电机鲁棒电流控制算法研究[J].中国电机工程学报，2013，33（15）：78-85; 13.

[4]    TURKER T， BUYUKKELES U， BAKAN A F. A robust predictive current controller for PMSM drives[J]. IEEE Trans. Industrial Electronics，2016，63（6）：3906-3914.

[5]    毋少楠，史军伟，李志新.基于ESO的PMSM无差拍预测电流控制研究[J].电气传动，2021，51（3）：22-28.

[6]    汪凤翔，何龙.永磁直线电机快速终端滑模预测电流控制[J]. 电机与控制学报，2023，27（6）：160-169.

[7]    柯栋梁.基于自适应观测器的永磁同步电机前馈无差拍预测控制[J].微特电机，2023，51（7）：46-50;66.

[8]    王晓琳，李紫佳，李正龙，等.超高速低载频比下永磁同步电机无差拍电流控制[J].电机与控制学报，2023，27（4）：55-63;74.

[9]    刘刚，张婧，郑世强，等.基于参数在线辨识的高速永磁电机无差拍电流预测控制[J].电机与控制学报，2023，27（9）：98-108.

[10] 舒朝君，柳林志.基于参数自适应的永磁同步电机无差拍预测电流控制[J].电力工程技术，2023，42（4）：175-184.

[11] ZHANG X， HUANG X. An incremental deadbeat predictive current control method for PMSM with low sensitivity to parameter variation[A]. 2020 International Conference on Electrical Machines （ICEM）[C]. Gothenburg， Sweden： IEEE， 2020：1060-1066.

[12] YUAN X， ZHANG C， ZHANG S. Novel deadbeat predictive current control for SPMSM drives with inductance and rotor flux linkage variation[A]. IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society[C]. Singapore， Singapore： IEEE， 2020： 1046-1051.

[13] WANG Z， YU A， LI X， et al. A novel current predictive control based on fuzzy algorithm for PMSM[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics， 2019， 7（2）：990-1001.