基于Delft3D的珠江前航道尸体模型漂移轨迹预测
程香菊 陈泽海 李斌 李旭 毕锦进 王龙威


摘 要:为预测珠江前航道中尸体的漂移轨迹,帮助当地水警确定溺亡者尸体的具体位置,利用 Delft3D构建珠江前航道水动力模型,并使用尸体模型进行了多次现场漂移试验。通过对珠江前航道表层流速进行拟合,建立了尸体模型漂移的预测模型,R2为0.88。研究结果表明,珠江前航道释放的尸体模型受潮汐和径流作用沿河道做往复运动,并呈逐渐漂向下游的趋势;漂移模型验证中尸体模型的漂移速度和方向基本与潮流一致,模拟结果的误差在1 km 以内,终点距离误差率小于15%;实例验证中成年女性尸体的模拟结果误差约为300 m;游船所引起的波浪力等外力导致漂移轨迹呈现出南北方向性的偏差,需要进一步提升模拟效果。该漂移模型的推导模式同样适用于其他感潮河段,可使尸体的漂移轨迹变得可测,为尸体打捞工作和警方的案件处理提供了便利和参考。
关键词:Delft3D;感潮河段;漂移轨迹;预测模型;拟合
中图分类号:TV21 文献标识码:A 文章编号:1001-9235(2024)05-0065-10
Prediction of Corpse Model Drifting Trajectories in Pearl River FrontChannel Based on Delft3D Model
CHENG Xiangju1, CHEN Zehai1, LI Bin2*, LI Xu2, BI Jinjin2, WANG Longwei1
(1. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510641, China;2. Marine Branchof Guangzhou Public Security Bureau, Guangzhou 510235, China)
Abstract: To predict the drifting trajectories of bodies in the Pearl River Front Channel and assist local water police in locating the specific positions of drowning victims, this study uses Delft3D to construct a hydrodynamic model of the Pearl River Front Channel and conducts multiple on-site drifting tests using a corpse model. By fitting the surface flow velocity of the Pearl River Front Channel, the paper builds a prediction model for corpse model drifting with an R2 of 0.88. The results show that the corpse model released in the Pearl River Front Channel undergoes back-and-forth motion along the river channel under the influence of tides and flows, gradually drifting downstream. In the drifting model validation, the drifting speed and direction of the corpse model are generally consistent with the tidal current, and the error in simulation results is within 1 km, with a final distance error rate of less than 15%. In a case study, the simulated results for an adult female corpse have an error of approximately 300 m. External forces such as wave force caused by boats result in a north-south directional deviation in the drifting trajectory, indicating the need to further improve the simulation effect. The derivation mode of the model is also applicable to other tidal rivers, making it possible to measure the drifting trajectories of bodies and providing convenience and reference for body recovery work and police case processing.
Keywords: Delft3D; tidal reach; drifting trajectory; prediction model; fitting
珠江前航道区域位于广州市主要的河流景观区,处于繁华地段且人流量大,偶有溺亡事件发生。根据李旭等[1]的统计,2003—2012年珠江航道广州段平均每年溺亡浮尸数量超过210具。此类溺亡事件常常需要当地警方在第一时间加以处理。而珠江前航道属于感潮河段[2],受潮汐的影响,河道的流量、水流和流向随时间不断变化,这导致航道中的尸体位置很难被迅速、准确地确定,从而给办案的警方带来极大的困难。若不能及时对尸体进行打捞或溯源,极易引发市民恐慌,造成不良社会影响,且大范围搜寻易给公安机关带来更多的人力、物力和财力负担。因此,预测水中尸体的漂移轨迹对民众和警方都具有至关重要的作用。
一般情况下尸体在水里的运移过程包括下沉、沉底、上浮以及漂移4个阶段[3],本文所研究的预测模型主要针对尸体运移的漂移阶段。关于水上目标漂移的轨迹预测问题,国外已经研发出了许多预测模型,如加拿大的 CANSARP[4]、美国的 HACSALV[5]和挪威的 LEEWAY[6]等。在国内,也有不少相关研究,例如刘同木等[7]运用龙格库塔数值方法,建立了考虑风、海流等因素的落水人员漂移轨迹模型。綦梦楠等[8]进行了南海海域表层漂流浮标轨迹试验,并以此建立关于浮标漂移速度的回归模型。曾银东等[9]通过海洋动力模型和拉格朗日粒子追踪相结合的方法,建立了福建近海物体漂移轨迹预测模式。上述预测模型均表明水上物体的漂移轨迹研究的关键是准确获取水流速度。目前,通常采用数值模型对水域进行模拟以获取水流速度,常用的数值模型包括 Delft3D、Mike、EFDC等。范宏翔等[10]利用 EFDC 二维水动力模型和基准期,量化了气候和人类活动对鄱阳湖水龄变化的影响。柴崇顼等[11]利用 Delft3D建立了受径流与潮汐相互作用的辽河口湿地海域的水动力学模型,并定量分析潮滩盐沼植被对水动力的影响。陈志琦等[12]基于 Mike21建立了罗源湾水动力数值模型,计算出罗源湾水体交换周期及纳潮量。其中,Delft3D模型已被广泛应用于中国近海地区感潮河段的水动力模拟[13-15],能较好模拟受径流和潮汐双重影响的河段,故本研究采用 Delft3D来模拟珠江前航道的流场。
当前,水上目标漂移轨迹的预测研究主要集中于海洋领域[16-19],而感潮河流与海洋有所不同,其河流流动受到潮汐的周期性影响,导致其呈现出往返周期性运动。为此,本文选取珠江前航道感潮河段作为研究区域,利用 Delft3D数值模型模拟了珠江前航道的流场,并在实地进行了尸体模型漂移试验。最后,在考虑水流和风等因素的条件下,将珠江前航道表层流作为自变量,建立了珠江前航道尸体模型漂移速度的线性回归模型,并利用该模型对试验轨迹进行验证,以证明该模型的有效性,以此为公安机关的案件处理提供参考,缩小尸体的搜寻范围,降低所需成本。
1尸体模型漂移轨迹试验
1.1试验区域
珠江前航道位于广东省广州市,是珠江水系的一部分,见图1、2。该地区位于珠江三角洲冲积平原北部,地势整体呈现南低北高的特征,其河道受到径流和潮汐的双重影响,潮汐类型为不规则半日潮。试验区域位于珠江西航道东南侧,毗邻珠江后航道北侧,被二沙岛环绕,河道西起人民桥,东至东圃特大桥,全长15 km。试验区域内河道宽度由上游至下游逐渐增加,其中上游人民桥段河道宽160 m,下游东圃特大桥段河道宽度则达到520 m。
1.2尸体模型的制作
在广州水警辖区内发现的尸体多以俯卧或仰卧的体位出现,其中俯卧的数量明显超过仰卧[1]。为模拟真实尸体漂浮在水面上漂浮的情形,采用不同形状的水瓶制作了与俯卧或仰卧相同形态的尸体模型,并进行了现场试验(图3)。该模型身高165 cm,内部充注淡水,体重55 kg,整体密度略小于水,其结构和水中姿态与真实尸体相似。为了监测漂移轨迹,尸体模型搭载了 GPS 定位器,定位器每10 s记录一次经纬度位置信息,并采用密封性塑料袋保护不受水损。
1.3漂移轨迹试验工况结果
在尸体模型漂移试验过程中,观察到尸体模型停靠码头、定位数据异常以及停止后重新漂移等情况,为了准确选取漂移轨迹,采用连续时间判别法,选取了漂移位置连续性高及时间尽可能长的漂移过程,最终筛选出5个漂移过程段,其起止时间和起始位置见表1。
图4给出了 JR1与 JR3漂移试验的轨迹线。从图4可以看出,JR1试验的尸体模型漂移轨迹起点位于江湾桥与海印桥之间,此时河流处于落潮,尸体模型开始朝下游方向漂移。随着涨潮的影响,尸体模型的漂移方向在华南大桥东侧发生改变并开始向上游漂移。当涨潮结束后,由于受到落潮与径流的影响,尸体模型漂移方向在猎德大桥西侧再次发生改变,从之前的向上游漂移转为漂向下游漂移。最终,尸体模型在琶洲大桥与东圃特大桥之间结束漂移过程。JR3试验的尸体模型在水警码头北侧开始漂移,当时河流处于落潮状态,尸体模型顺流而下,最终在猎德大桥与华南大桥之间结束漂移。
图5给出了 JR2、JR4与 JR5漂移试验的轨迹线。从图5可以看出,JR2试验的尸体模型在中大码头东北侧开始漂移,在河流处于落潮时向下游漂移。当尸体模型到达猎德大桥东侧时,尸体模型的漂移方向在涨潮作用下发生改变,开始向上游漂移,最终尸体模型在猎德大桥下结束漂移。JR4试验的尸体模型漂移轨迹起点为广州水警码头东北侧,当时河流正处于为落潮,尸体模型沿着河道往下游漂移,并最终在广州大桥与猎德大桥之间结束漂移。JR5尸体模型漂移轨迹的起点位于海珠桥西侧,此时河流正处于落潮时期,尸体模型顺着航道向下游漂移。当尸体模型漂移至广州大桥西侧时,漂移方向受到涨潮的作用发生改变,开始朝上游漂移。最终,尸体模型于广州大桥西侧结束漂移。
采用中大水文站所在的断面作为潮位参考断面,对漂移试验期间的水位变化与尸体模型漂移方向进行分析。图6中A、B、C、D 点分别为试验期间的每个潮周期内落憩、涨急、涨憩和落急4个特征时刻。
在 JR1试验中,珠江前航道经历了2次落潮和一次涨潮。尸体模型从试验开始至落憩时刻向下游漂移,漂移距离达到了7596 m。接着,从落憩时刻到涨急,再到涨憩时刻,尸体模型改变方向朝上游漂移,而漂移距离仅为2848 m。从涨憩时刻到落急时刻,尸体模型再次转变方向朝下游漂移,漂移距离为6008 m。从 JR1试验不难看出由于受到径流和落潮的双重影响,尸体模型在涨潮时的漂移距离远远小于2次落潮的距离。
在 JR3和 JR4试验中,珠江前航道先后经历了一次落潮和一次涨潮,但是2次试验的尸体模型漂移方向均未发生改变始终朝向下游。这是由于该时期处于丰水期,河道受到径流影响较大,其涨潮的影响被削弱,使得河道中的水流方向在落憩之后仍朝向下游,致使尸体模型在落憩时刻之后继续朝下游漂移。
在 JR2和 JR5试验中,珠江前航道先后经历了一次落潮和一次涨潮。试验开始后,尸体模型一直向下游漂移,但受径流的影响,2次试验的尸体模型在落憩时刻并未改变漂移方向。直到落憩至涨急之间的某个时刻,尸体模型才改变漂移方向朝上游漂移。JR2和 JR5尸体模型朝下游的漂移距离分别为3839、5296 m ,而朝上游的漂移距离仅为488、22 m,远小于朝下游漂移的距离。
试验结果表明,珠江前航道受到潮汐和上游径流的双重影响,落潮时河流的势能变化大于涨潮时的势能变化,从而使得落潮时的河流动能大于涨潮时的河流动能,进而导致尸体模型呈现出周期性的往复运动并逐渐向下游漂移。
2水动力学模型构建
2.1控制方程
本文采用 Delft3D模型作为计算平台,该模型是由荷兰 Delft 公司开发的一套功能强大的软件包。使用水动力模块对珠江前航道流场进行模拟研究。该模块控制方程是在浅水和 Boussinesq 假定下,求解不可压缩流体的纳维-斯托克斯方程(Navier- Stokes Equation),其中的垂直动量方程不考虑垂直加速度。该方程在水平方向采用正交曲线坐标系(ξ , η),在垂直方向采用σ坐标系。
深度平均的连续性方程:
式中 ζ——水位,m;t——时间,s;η、ξ——曲线和水平坐标;、 ——ξ和η方向的坐标转化系数,m;d——水深,m;U——ξ方向的水深平均流速,m/s;Q——由降雨、蒸发等引起的单位面积水的流入和流出,m/s。
ξ和η方向动量方程为:
式中 u、v、w——正交曲线坐标系下的流速分量, m/s;f——科氏力,1/s;Pξ、Pη——η、ξ方向的压强梯度,kg/(m2·s);Fξ、Fη——η、ξ方向的水平雷诺应力,m/s2;Mξ、Mη——η、ξ方向源项和汇项的动量分量,m/s2;υV——垂向黏性系数,m/s2;ρ0——水密度,kg/m3。
垂直坐标σ的表达式为:
式中 z——垂直方向的坐标,模型参照面上取0,向下至底部为水深 d;ζ——相对于参照面的水位;H——全水深;σ=0表示自由面;σ=-1表示河底。
k-ε湍流模型的表达式为:
式中 k ——湍流动能;ε——运输方程中的耗散 率;Pk ——能量生成项;Bk ——浮力项; v mol ——分子黏性系数;v3D——三维紊流系数;σk——垂向的坐标位置。
2.2计算方法
2.2.1河道网格化
利用 Delft3D-RGFGRID 模块对研究区域河道进行划分,见图7,划分的网格为正交曲线网格,并要使网格角度的余弦值小于0.02。本次研究区域长度约15 km,主河道宽度为160~520 m,进行网格收敛性测试后,确定单个网格的尺寸为5~33 m,生成有效的网格总数为31860个。生成网格后,通过 QUINKIN模块导入地形散点数据文件,把网格处的地形数据进行三角插值与内部扩散,所生成的即为研究区域网格相对应的地形值。
2.2.2计算条件设置
为减小模型发散的可能性,初始水位选择上下游边界水位的中间值,取0 m。上游边界的走向与人民桥一致,其边界条件为广州站点2022年6月1日至7月31日时间序列的水位资料,下游边界的走向与东圃特大桥一致,其边界条件为黄埔站点对应时间序列的水位资料。选取 k-ε湍流模型,通过模型稳定性测试以及考虑到尸体模型的漂移速度,确定时间步长为3 s。
2.3模型率定和验证
采用糙率表征河床阻力,并使用曼宁公式计算糙率,通过多次的率定确定了水平和垂直方向的糙率值为0.025。对水平方向的黏滞系数进行了多次率定,最终确定其数值为10 m2/s。
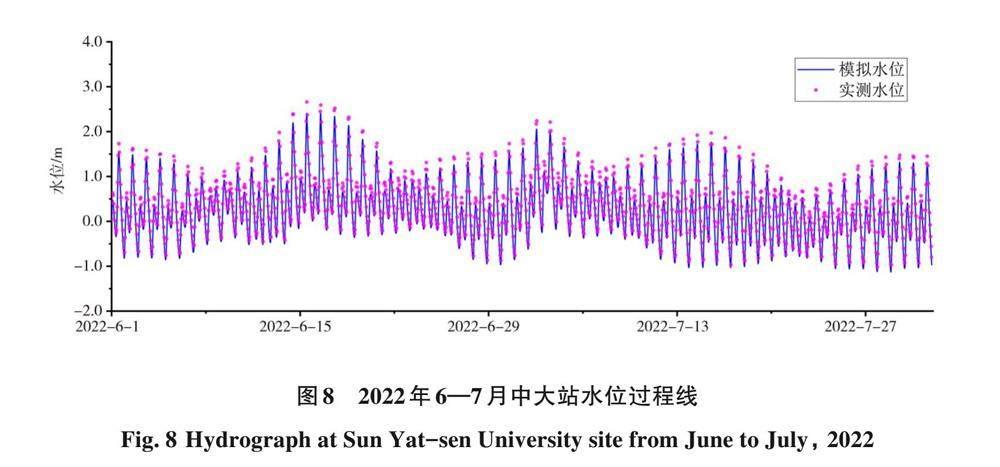
根据研究区域的位置,选择中大站点的实测水位资料作为验证资料。水位验证的时间跨度为61 d,即从2022年6月1日0:00到2022年7月31日22:00,形成了连续的水位时间序列。图8为2022年6—7月的中大站点水位过程线,从图中可以看出,中大站点计算水位值与实测水位值的符合程度较好,涨潮和落潮的水位趋势基本保持一致。
通过计算纳什效率系数(NSE)、平均绝对误差(MAE)和均方根误差(RMSE)可以定量衡量模型的模拟值与实测值的一致程度,经计算得到 NSE 为0.94,MAE 为0.14 m,RMSE 为0.14。综合来看,本研究利用 Delft3D所构建的数值模型精度、可信度较高,能够较好模拟珠江前航道的水动力过程,可以用于尸体模型漂移轨迹预测的进一步研究。
3尸体模型漂移轨迹数值模拟
3.1漂移预测方程构建
水上漂移的物体会受到风、流、浪的作用,对内河河道而言,波浪的波高相对较小,可以忽略波浪对漂移物体的影响[3]。基于此,本文认为珠江前航道中漂浮物体主要受水流的作用影响。然而,有关水流在漂移运动的贡献系数相关研究中没有达成统一的结论[20]。为解决这一问题,本文将尸体模型看作一个形状相同的固体物,以代表真实尸体,并采用线性回归方法,将表层流作为自变量,建立珠江前航道尸体模型漂移速度的回归方程,以此确定尸体模型的漂移速度和表层水流两者间的关系。
为得出表层水流流速与其他因素对尸体模型漂移的影响,先根据试验数据中的不同时间段的漂移距离求出尸体模型的漂移速度,然后再将漂移速度分解成东西和南北2个方向的分量,最后结合流场的表层流流速进行线性拟合。同时,考虑到航道中对轨迹预测误差的要求相对较小,以及船只、风等因素导致的不确定性较大,为在模型拟合中综合考虑这些复杂因素,引入了常数项 b,拟合公式如下:
式中 U——尸体模型的漂移速度,m/s;U'——表层水流速度,m/s;a——表层水流对漂移的影响系数;b——风、波浪、船只等对尸体模型漂移的综合影响项。
本研究对尸体模型漂移试验轨迹进行了如下分析,每隔10 s记录一次尸体模型位置并计算漂移速度,并根据水动力模型流场的输出结果,在相同时间和位置记录表层水流速度数据,时间间隔同样为10 s,共获得8333组相同时间段和位置的尸体模型漂移速度和表层水流速度数据。随后,采用统计学分析尸体模型漂移速度和表层水流速度的相关性,见图9。最终确定了珠江前航道尸体模型漂移的拟合公式为:
回归方程(7)的统计量 F 为56918.53,显著水平p=0<0.05。因此,可以认为该回归方程具有统计学意义[21]。该回归方程式的决定系数 R2为0.88,表明该方程具有良好的相关性。
3.2漂移模型验证
为验证上述回归模型拟合公式的有效性,本文利用式(7)对5次试验轨迹进行了模拟计算。在此过程中,将流场按照漂移速度的东西和南北2个分量进行分解。以试验初始位置和起始时间为基础,每隔10 s进行一次漂移距离的迭代计算,直至模拟漂移轨迹结束,以此获取尸体模型的终点位置。
回归模型模拟5次试验轨迹的终点偏移距离与终点距离的误差率见表2。表2可以看出,在5次试验模拟中,JR1的漂移总距离最大,其终点偏移距离也最大,而 JR2的终点距离误差率最大。5次试验模拟的终点偏移距离均不超过1 km,终点距离误差率均不超过15%。从终点的误差情况来看,模拟的效果相对准确。
图10展示了5次试验实际轨迹与回归模型拟合轨迹的对比情况。在 JR1模拟试验中,虽然拟合的尸体模型漂移速度和方向与实测变化趋势整体一致,但终点距离误差达到了825 m。这是由于在涨潮期间,游船经过产生的波浪力等外力使得尸体模型漂向岸边,导致拟合轨迹与实际轨迹存在显著偏差。在 JR2、JR5模拟试验中,虽然模拟轨迹的整体距离误差较小,但是在涨潮期间,拟合的轨迹存在方向性的偏差,主要原因是试验中的尸体模型漂移受到了游船波浪等外部因素的干扰,产生了南北方向的偏差,这也使得 JR2的终点距离误差率远大于其他4次试验。在 JR3、JR4模拟试验中,拟合的尸体模型漂移速度和方向与实测变化趋势基本一致,拟合的漂移轨迹与实际轨迹吻合度较高,终点距离误差较小,分别为113、216 m。
根据5次试验的漂移情况,本文利用漂移开始的3 h 内漂移轨迹偏移距离和距离误差率来评估漂移轨迹预测过程的准确性(图11)。根据误差统计,5次试验中的预测轨迹在试验开始3 h 内的偏移距离均小于800 m,距离误差率均小于15%,这表明该预测模型在珠江前航道区域总体上表现出较高的准确性。值得注意的是,JR3试验的最大偏移距离和最大距离误差率均为5次试验中的最大值。这是因为在 JR3试验中,尸体模型漂移至江湾大桥时靠近岸边并沿着岸边继续漂移,直至海印大桥东侧才离开岸边漂向河道中心。由于尸体模型在岸边漂移时的速度小于沿河道中心漂移时的速度,因此 JR3试验尸体模型预测轨迹在接近2 h 时的偏移距离和距离误差率均达到最大值。
综合来看,对于在试验中沿河道中心漂移的尸体模型,采用回归模型可以较好拟合其漂移速度,并且能够较为准确地模拟尸体模型的漂移轨迹;而对于在试验中靠岸漂移的尸体模型,模型的模拟效果仍有待提高。建议增加试验次数,进一步分析尸体模型靠岸漂移的影响因素来优化模型,以更好地模拟尸体模型靠岸漂移的轨迹。
3.3实例验证
利用一个真实案例进行模拟计算,以验证上述漂移模型的准确性。案例描述如下:一名成年女性于2023年7月24日15:00在猎德大桥附近落水,其尸体于2023年7月25日17:56在华南大桥东侧被发现。据广州市水上公安局的分析,预计该尸体上浮时间为2023年7月25日10:20,漂移时间段内河流的状态为:落—涨—落,且上浮地点与落水地点相同,即猎德大桥。基于该实际案例的信息,利用上述漂移模型进行轨迹模拟,得到的计算结果见图12。
模拟轨迹的起始位置为猎德大桥,此时河流处于落潮状态,尸体沿着下游方向漂流至琶洲大桥东侧,随着涨潮的影响,尸体开始向上游漂移,当尸体接近华南大桥时,受落潮影响再次漂向下游,最终于该桥东侧被发现。与实际的尸体发现位置相比,模拟结果非常接近,距离误差约为300 m。这一案例验证了漂移模型的准确性,为类似事件的调查和分析提供了有力支持。
4结论
本文利用 Delft3D 输出的珠江前航道流场数据作为回归自变量,建立了尸体模型漂移速度的回归模型,并模拟了2022年6—7月的5次尸体模型漂移试验轨迹。通过对比回归模型的拟合轨迹与实际轨迹,得到以下结论。
a)珠江前航道中的尸体模型受到潮流和径流的双重影响,呈现出周期性的往复运动。由于落潮时的河流动能大于涨潮时的河流动能,尸体模型呈现出向下游漂移的趋势。
b)拟合得到回归模型在试验轨迹的验证中表现良好,能够较好地拟合尸体模型漂移速度,并且在实例中也得到了验证,其模拟结果能满足偏移误差小于1 km 的要求。
c)虽然内河漂移模型无需考虑波浪的作用,但珠江前航道常有大型游船通行,游船所引起的波浪对尸体模型漂移有着不可忽视的影响。这种影响很容易导致试验轨迹呈现南北方向的偏差,可通过进一步的试验来分析尸体模型受这一影响而沿岸漂移的情况,并优化模型以改进模拟效果。
在未来的研究中,需要针对不同身高和体重的尸体进行更多的珠江前航道尸体模型漂移试验,并在漂移试验过程中监测风和流的数据,以推导更准确的回归模型。此外,还需进一步提高水动力模型的精度,以提高轨迹模拟的准确性。
参考文献:
[1]李旭,林彬.2291具浮尸的回顾性分析[J].广东公安科技,2016,24(4):78-80.
[2]雷列辉,黄伟杰,王建国,等.珠江前航道表层沉积物中镉污染评价及其含量分布情况[J/OL].人民珠江:1-8[2023-11-19]. http://kns. cnki. net/kcms/detail/44.1037. TV.20230613.1227.016. html.
[3] DILEN D R. The motion of floating and submerged objects in the Chattahoochee River, Atlanta, GA[J]. Journal of Forensic Sciences,1984,29(4):1027-1037.
[4] HILLIER L E. Validating and improving the Canadian coast guard search and rescue planning program( CANSARP)oceandrift theory [D]. Newfoundland: Memorial University ofNewfoundland,2008.
[5] TURNER A C , LEWANDOWSKI M J , LESTER S, et al. Evaluation of Environmental Information Products for Search and Rescue Optimal Planning System(SAROPS)– Version for Public Release [R]. National Technical Information Service,Springfield,2008.
[6] ALLEN A A. Leeway divergence[R]. US Coast Guard Research and Development Center,2005.
[7]刘同木,张炜,曹永港,等.基于受力分析的落水人员漂移轨迹预测研究[J].海洋预报,2017,34(1):66-71.
[8]綦梦楠,张娟.基于回归模型的南海表层漂流浮标轨迹模拟研究[J].海洋预报,2021,38(4):87-98.
[9]曾银东,郭民权,方许闻,等.福建近海漂移物漂移轨迹分析及模拟[J].厦门大学学报(自然科学版),2023,62(3):435-443.
[10]范宏翔,徐力刚,朱华,等.气候变化和人类活动对鄱阳湖水龄影响的定量区分[J].湖泊科学,2021,33(4):1175-1187.
[11]柴崇顼,赵梓宇,弓耘,等.盐沼植被作用下的辽河口三维水动力数值模拟[J].水动力学研究与进展 A 辑,2022,37(3):415-425.
[12]陈志琦,逄勇,张倩,等.基于水动力数值模拟的罗源湾水体交换周期及纳潮量计算[J].水资源保护,2022,38(3):125-130.
[13]李嘉,郑向阳,张华,等.基于 Delft 3D模型的感潮河口示踪模拟[J].海洋科学,2020,44(10):23-32.
[14]戴文鸿,胡涛,丁梦娇,等.感潮河段交汇区水流特性数值模拟:以宁波三江口为例[J].南水北调与水利科技,2018,16(6):171-177.
[15]李林娟,童朝锋.基于 Delft3D-flow模型的长江口盐度扩散规律模拟[J].人民长江,2016,47(23):107-111.
[16]CHEN Y,ZHU S X,ZHANG W J,et al. The model of tracing drift targets and its application in the South China Sea[J]. Acta Oceanologica Sinica,2022,41(4):109-118.
[17]谭鹏,谭乐祖,张峥,等.海上自由物体漂移轨迹预测方法[J].计算机与数字工程,2021,49(1):105-110.
[18]朱岿,牟林,王道胜,等.海上搜救辅助决策技术研究进展[J].应用海洋学学报,2019,38(3):440-449.
[19]高松,徐江玲,艾波,等.基于 SOA 架构的国家海上搜救环境服务保障平台研发与应用[J].海洋预报,2019,36(3):71-77.
[20]张娟,杨阳,周水华,等.莺歌海海域漂移物漂移特征分析[J].海洋预报,2013,30(3):73-77.
[21]BENJAMIN D J,BERGER J O ,JOHANNESSON M ,et al. Redefine statistical significance[J]. Nature Human Behaviour,2018,2(1):6-10.
(责任编辑:李泽华)

