基于海表温度和随机森林的珠江流域干旱预报模型研究

冯鑫 刘艳菊 童宏福 钱姝妮

摘 要：海表温度（Sea Surface Temperature，SST）是干旱预报的主要因子之一，传统预报模型主要采用固定海域 SST （如 ENSO），未从全球大范围角度搜寻可利用的 SST信号。通过回归分析筛选全球具有预报意义的 SST 区域，结合随机森林算法构建了一种气象干旱预报新模型，以珠江流域为例进行应用检验。结果表明：①该模型可有效预报干旱的时空变化规律，且预见期越长，预报精度相应下降；②非汛期干旱预报准确率高于汛期，沿海地区比内陆地区有更好的预报效果；③珠江流域干旱发生可能与典型的气候波动有关，如厄尔尼诺南方振荡和北大西洋振荡。

关键词：干旱预报；海表温度；随机森林；珠江流域

中图分类号：TV21 文献标识码：A 文章编号：1001-9235（2024）05-0096-07

Drought Prediction Model of Pearl River Basin Based on SST and Machine Learning

FENG Xin1， LIU Yanju2， TONG Hongfu3， QIAN Shuni4*

（1. School of Civil Engineering and Transportation， The South China University of Technology， Guangzhou 510640， China;2. Comprehensive Technology Center of Pearl River Water Resources Commission of Ministry of Water Resources，Guangzhou 510611， China;3. Qingyuan Hydrology Sub-bureau of Guangdong Province， Qingyuan 511599， China;4. Guangzhou Water Planning Survey and Design Institute Co.， Ltd.， Guangzhou 510665， China）

Abstract： Sea surface temperature （SST） is one of the main factors for drought forecasting. Conventional forecasting models mainly use SST from fixed sea areas （e. g. ， ENSO）， without searching for available SST signals from a global large-scale perspective. Combining with the random forest algorithm， this paper constructs a new meteorological drought forecasting model through regression analysis to screen global SST areas of forecasting significance and takes the Pearl River Basin as an example for application tests. The results are as follows.① The model can effectively forecast the temporal and spatial evolution of drought， and as the forecast period becomes longer， the forecast accuracy decreases accordingly.② The accuracy of drought forecast is higher in non-flood season than in flood season， and the coastal area has a better forecast effect than the inland area.③ The occurrence of droughts in the Pearl River Basin may be related to typical climate fluctuations， such as the El Ni?o Southern Oscillation and the North Atlantic Oscillation.

Keywords： drought predication; sea surface temperature; random forest; Pearl River Basin

干旱灾害是最主要的自然灾害之一，对区域水资源、自然生态环境、农业生产、社会经济发展等有很大的影响和破坏［1-2］。及时可靠的干旱预报可以帮助制定和实施可行的抗旱措施，从而避免和减少可能的干旱损失。干旱指数是刻画干旱灾害的重要工具，按照干旱类型可划分为气象干旱指数、农业干旱指数、水文干旱指数及社会经济干旱指数等。气象干旱指数一般基于气象因子构建，最常用的气象干旱指数有帕尔默干旱指数（Palmer Drought Severity Index，PDSI）［3］、标准化降水指数（Standardized Precipitation Index，SPI）［4］和标准降水蒸散指数 （Standardized Precipitation Evapotranspiration Index， SPEI）［5］。其中，标准化降雨指数（SPI）是计算最简单、应用最广的干旱指数之一［6-8］。

目前，干旱预报模型大致可分为两类，即动力数值模型和统计模型。动力数值模型物理机制明确，但模型结构和参数繁多，计算量大且复杂，通常需要具备一定的专业基础，并且局部地区模型预报结果存在较大的不确定性和误差［10-11］。统计模型则是利用线性或非线性数理统计方法，通过建立预报对象（干旱）与大气环流、海温等预报因子之间的相互关系实现预报功能［12］。相比动力数值模型，统计模型结构简单、应用简便，在某些场合预报效果甚至优于动力数值模型，得到众多学者的青睐［13-14］。如 Ali 等［15］提出多元经验模态分解模型，耦合智能算法，构建基于 SPI 的干旱预报模型，应用于巴基斯坦干旱预报，呈现了良好的预报效果。Feng等［16］运用随机森林，基于澳大利亚小麦产区的 SPI 与 ENSO 相互关系，构建干旱预报模型。

研究表明，干旱灾害与海洋表面温度场（SST）有密切联系，因此不少学者采用 SST作为主要预报因子来建立干旱统计预报模型［17-19］。Funk 等［20］基于 SST 构建了西太平洋梯度指数和中印度洋指数，建立了东非春季干旱预报模型。Liu等［21］利用标准化 SST、200 Pa 和500 Pa气压高度场，构建了适用于中国地区的季节性干旱预报模型，基于与干旱相关的 SST，建立了大尺度和区域尺度的干旱预报模型。然而，现有研究对 SST 的提取多数仅局限于一个或几个海域，如 ENSO 活动区，缺乏对其他海域的考虑，即从全球范围内搜寻 SST预报因子，导致未能充分利用 SST有用信号。另外，传统的研究较少解释 SST 与区域干旱之间的影响机制。基于全球 SST信号，构建基于随机森林模型的1～3个月预见期的干旱预报模型，以珠江流域作为研究区进行论证，为干旱预报领域提供新的方法思路，同时为珠江流域干旱灾害防灾减灾提供支撑。

1研究区域和数据

1.1研究区概况

珠江流域位于中国东南部，是中国的第三大流域，总面积为45.4万 km2。海拔由西南向东北逐渐降低。流域上游因喀斯特地貌广泛分布而极易形成干旱，下游的粤港澳大湾区是重要的城市群以及重要的经济带。全年平均温度较高，多年平均气温为14～22℃ ， 属亚热带季风气候。珠江流域雨量充沛，在中国属于高位，年均降雨量为1600 mm，但雨量分布十分不均，空间差异性明显，时间上以春夏为主，枯水期主要发生在冬季（11月至来年3月）［22］。1.2数据来源

本研究 SST数据采用美国国家海洋和大气管理局提供的全球1?×1? 空间分辨率 COBE 海温数据集（https：//www. psl. noaa. gov）。时间跨度为1854年1月1日至2019年12月31日，共166 a数据。

本研究降水数据采用英国气候中心（CRU）提供的珠江流域0.5?×0.5? 空间分辨率月降水量数据集（https：//sites. uea. ac. uk/cru）。时间跨度为1901年1月1日至2019年12月31日。

2研究方法

2.1标准干旱指数（SPI）

标准干旱指数（SPI）是一个标准化指数，基于当地雨量的长期气候状况，反映某观测雨量可能出现的机会率。SPI指数可以在不同的时间尺度和空间尺度上使用同一个干旱指标反映其干旱状况，从而能较好地反映和比较干旱强度和持续时间等，因此得到广泛应用［23］。SPI 可应用于不同的时间尺度（如3、6和12个月），以分析干旱对各种水资源需求的影响。本研究选择3个月时间尺度的 SPI（SPI-3）作为干旱预报对象［24］。传统上，SPI-3按月变化，反映过去3个月的累积降水量，适合流域尺度的研究。同时，大气环流因子与干旱指数在3个月间隔时具有更强的相关性。SPI具体计算步骤［25］如下。

a）假设某时段降水量为随机变量 x，则其 r 分布的概率密度函数为：

式中 β、γ——相关尺寸参数；Γ（γ）—— Gamma 函数。

b）对 r 分布概率进行正态标准化处理，即：

式中 t =；P——降水量 x 小于当前 x0事件的概率，当 P >0.5时，S =1，当 P ≤0.5时， S=-1； c0=2.515517， c 1=0.802853， c2=0.010328，d 1=1.432788，d2=0.189269，d3=0.001308。

由式（2）求得最终结果即是此降水序列的 SPI。在干旱事件识别中，需要设置一个阈值来划分时间序列中的干旱事件/月份，本研究将 SPI 阈值设置为-1，该阈值能较好地平衡极端事件的数量。

2.2随机森林模型

随机森林（Random Forest）是一种基于统计学习理论的组合分类或回归方法，具有较高的准确性和稳定性，主要计算方法是通过对多个分类回归树（Classification And Regression Tree，CART）的预报 进行组合合并，最后通过投票方式得到最终预报结果。Breiman 和 Culer 于2001年基于 Ho 提出随机决策森林，采用自组采样法（Bootstrap Sampling）对原始数据进行有放回的抽样，生成众多分类树，最终把分类树组合成随机森林。在完成所有的决策树的构建后，随机森林算法使用集成策略来预测新的样本的类别或值［26-27］。具体地，对于一个新的样本，随机森林将该样本输入到所有的决策树中，然后统计每个类别的出现次数，最终选择出现次数最多的类别作为预测结果。

在建模过程中，随机森林所需要调整的参数较少。其中需要确定对原始数据集进行有放回抽样生成的子数据集个数，即决策树的个数。决策树太小容易欠拟合，太大不能显著地提升模型，所以选择适中的数值。本研究经过参数率定，RF模型决策树选取200，其他参数设置为默认参数。所选取的参数已经满足本研究模型要求的稳定性和预报准确性。本研究 RF 算法采用 R 语言软件中的“Random Forest ”包来驱动预报模型。

2.3干旱预报模型构建

在本研究中，利用 RF 算法来构建干旱预报模型。当预报因子与预报对象通过回归分析进行筛选时，它们之间的关系可能并不是线性相关的，机器学习算法可以挖掘出潜在的非线性关系，从而提高预报效果。

挑选具有预报标准降水指数能力的海温网格场，在本研究中，需要设定一个显著性评价水平α判 断海温和 SPI是否具有较好的相关性。根据皮尔逊检验法，阈值的选取与数据长度和显著性水平选取相关。特别地，当数据长度为 k =90时，选取（k-1）且置信水平为95%时的α≈0.207。当确定阈值后，计算网格海温时间序列与1～3月提前期的干旱指数（SPI）的皮尔逊检验值，同时按以下要求挑选海温网格。

第一步，将大于海温序列同标准干旱指数的相关系数的阈值挑选出来，并确定其在全球海温场的位置。

第二步，提取所选海温网格的历时枯水期时间数据，对其检验噪声项。检验方法为挑选无效值出现次数占比大于40%的网格，并将其剔除。

第三步，无效值的识别主要关注海温数据。同一海温格点，提取的数年同月海温数值未发生变化视为无效值。

本研究在全球海温网格中搜索与研究区满足显著相关性的单海温因子，划分 SPI数据集1901—1990年前90 a 为率定期，1990—2018年为检验期构建模型，利用上文所述的海温格点集合数据和珠江流域 SPI干旱指数构建基于随机森林算法的气象遥相关模型。

2.4 模型评价指标

在这项研究中，以观测 SPI 为对照，通过对干旱预报模型预报值进行对比分析，以评估该模型的准确性和适用性。选用皮尔逊相关系数 CC（Pearson Correlation Coefficient）、漏报率 MAR（Missing Alarm Rate）和误报率 FAR（False Alarm Rate）共3种指标作为精度评估指标。CC 决定了预报和观测之间的相关程度，其值为-1～1。CC 值为1表示预报和观测之间完全正相关，而-1表示完全负相关。 CC 表示为：

式中 Xt ——观测的数据；Yt ——预报的数据；

Xi ——观测数据的平均值；Yi——预报数据的平均值。

MAR 反映了实际发生但被预报遗漏的干旱事件占发生干旱事件的比例；而 FAR 反映了未发生干旱事件被预报为发生干旱占发生干旱事件的比例。 MAR 和 FAR 均值越小，性能越好，表示为：

MAR =          （4）

FAR =          （5）

式中 TP——实际发生干旱最终预报结果为真的事件数量；FP——实际未发生干旱最后预报得到的结果却为真；FN——实际发生干旱最后预报得到的结果却为假。

3 结果与分析

3.1 模型精度评估

3.1.1 率定期精度评价

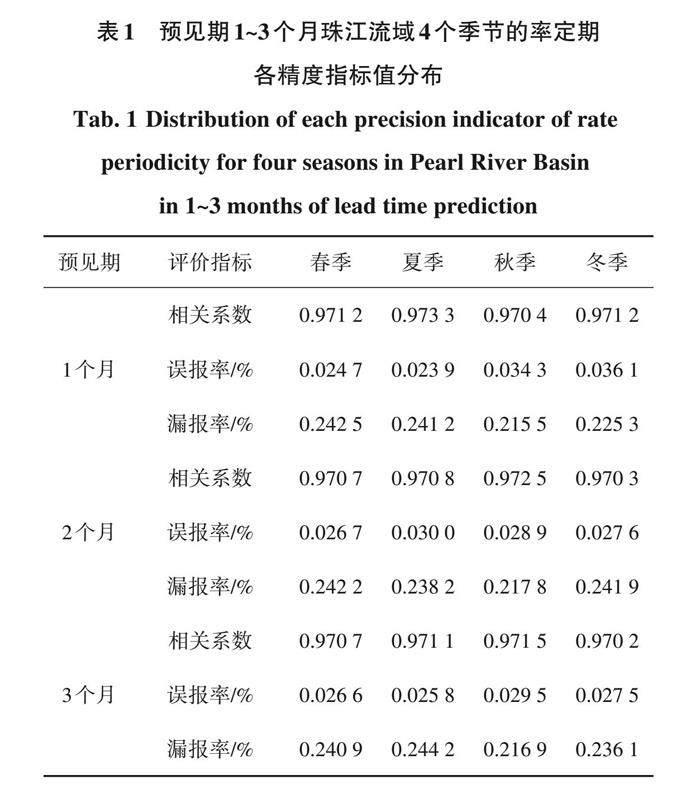
预见期1～3个月的4个季节的率定期各精度评估指标的分布情况见表1，结果显示：在所有时期的率定期中，干旱指数预报值和实际值拟合优良，相关系数 CC 均达到0.97以上，误报率均在0.025左右，漏报率在0.25左右，取得了较为理想的率定效果。从不同预见期看，预见期1个月的率定期精度明显高于其他2个月份。预见期越长，预报精度相应下降。对比各季节相关系数（CC）的率定期结果差异，夏季的模型拟合效果最优异，CC 值达到了97.3%。其他月份稍微偏弱，CC 值均在97%附近接近于显著相关系数。夏季模型的误报率和漏报率均属于最低的。综合而言，模型率定效果优良。

3.1.2 检验期相关系数

图1显示了珠江流域预见期1～3个月不同季节的相关系数的空间分布模式。从空间分布上看，珠江流域的空间分布高相关性区域主要集中在流域的东南部，东部明显高于西部，预报效果最差的网格出现在夏天的流域西北部区域。从不同预见期的角度上看，不同预见期的相关系数的空间模式相似，其中预见期1个月的预报结果具有更高的相关性，相关值比其他预见期 CC 值高出0.1左右。从不同季节的角度可以看出，春天和冬天的相关系数明显高于夏天和秋天，高相关性的区域分更广，相关性良好网格主要集中在东部。表明了春季和冬季的干旱与海面温度的联系更为密切。夏天的模型效果是所有季节中最低的，CC 值大多数接近-0.2，主要集中在中西部。秋天的相关系数空间模式与夏天相似但 CC值更高。综上所述，预见期1个月预报效果最好，特别是春天和冬天的预报结果，相关系数高的网格占比更多。结果表明：空间上，靠近海洋的地区可能有更强的陆地-海洋相互作用效应，近海地区气候受海洋的影响比内陆地区更明显；时间上，流域枯水期（春天和冬天）模型预测结果更精准，流域汛期（夏天和秋天）模型预测结果较差。这可能源于干旱期流域降水更容易受海洋气候影响。

3.1.3检验期错误率和误报率

图2显示了12个月预见期1～3个月的误报率和漏报率箱形图。可以发现，在3种预见期中，预见期1个月的预报准确率最高，误报率为20%～40%，异常数据为60%～80%。从月份角度而言，1—4月的误报率和漏报率低于其他月份，结果在10%到20%之间。而11、12月的误报率和漏报率则远远高于其他月份的，特别地，12月的结果在预见期1～3月的均是最差的。预报结果在春季和冬季更准确。值得注意的是，预见期1～2个月的结果明显地显示出，1—6月上半年的误报率低于7—12月，而这一结果并未在漏报率中体现。在预见期3个月结果中，所有月份的误报率和漏报率几乎没有太大的差异。

3.2 SST影响干旱的可能机制

为了揭示 SST 影响干旱的物理机制，对于珠江流域，选取预见期1个月下的上中下游3个枯水期发生干旱频率最高的中心网格进行全球海面温度场的相关系数结果展示，分析了全球相关海温场影响珠江流域不同区域发生干旱的空间分布模式。图3a 为下一月份影响珠江流域上游干旱的 SST 空间分布。其中，具有95%显著负相关性的 SST 区域主要分布在 ENSO 和 IOD 活跃的赤道太平洋东部和印度洋全区。图3b 为下一月份影响珠江流域中游干旱的 SST 空间分布。其中，显著负相关性的海域主要分布在 ENSO 和 IOD 活跃的赤道太平洋东部和印度洋全区，显著正相关性的海域为南极涛动活跃区域。图3c描述了2月份影响珠江流流域下游干旱的 SST 空间分布情况。对干旱有影响的 SST场主要分布在 ENSO 活跃的赤道东太平洋和南太平洋地区。综上而言，影响珠江流域上中下游网格的海温场在全球海域的分布较为统一，最为明显的属 ENSO。同时，模型在预见期一个月的枯水期具有更高的预报精度，所展示的全球海面温度场更具代表性。结果说明本研究提出的干旱预报方法在预报因子的筛选上具有合理性。

4结论

a）以珠江流域 SPI-3作为预报对象，SST作为预报因子，利用海温大数据和 RF 算法构建了一种新的气象干旱预报模型。

b）为了评估干旱预报模型的性能，将模型用于干旱事件频发的珠江流域，对预报对象进行预见期1～3个月的预报。结果表明，该模型在珠江流域应用效果较好，预见期1个月预报准确率比其他2个 月更高。此外，非汛期干旱预报准确率高于汛期，沿海区域的预报准确率高于内陆区域，流域东部预报准确率高于流域西部。

c）预报模型中筛选的全球海面温度场主要来自各个典型海洋振荡海域，表明珠江流域干旱与一些典型的气候波动（如 ENSO 和 NAO）之间可能存在关系。本文所提出的方法为珠江流域提供了一个有效的干旱预报方法，同时也可以应用于其他领域，帮助水资源综合管理和流域干旱风险缓解。

参考文献：

［1］张青雯，崔宁博，赵禄山，等.基于相对湿润指数的云南省季节性干旱变化特征［J］.干旱地区农业研究，2020，38（4）：278-284.

［2］闫昕旸，张强，闫晓敏，等.全球干旱区分布特征及成因机制研究进展［J］.地球科学进展，2019，34（8）：826-841.

［3］ PENMAN H L. Natural Evaporation from Open Water，Bare Soil and Grass［C］//Proceedings of the Royal Society of London，1948.

［4］ MCKEE T B，DOESKEN N J，KLEIST J. The Relationship ofDrought Frequency and Duration to Time Scales［C］//Eighth Conference on Applied Climatology，California，1993.

［5］ VICENTE-SERRANO S M，BEGUER?A S，L?PEZMORENO J I. Amultiscalar drought index sensitive to global warming：the standardized precipitation evapotranspiration index［J］. Journal of Climate，2010，23（7）：1696-1718.

［6］梅晓丹，李丹，田静，等.2000－2018年黑龙江省干旱时空特征分析［J］.测绘工程，2022，31（3）：16-22.

［7］赵水霞，周泉成，王文君，等.基于 SPI指数的内蒙古地区干湿气候特征［J］.中国水利水电科学研究院学报（中英文），2022，20（1）：10-19.

［8］苑希民，张家铭，滕振敏.基于 SPI 指标左江流域旱涝演变规律与趋势预报分析［J］.水力发电，2022，48（1）：31-38.

［9］ FENG X，PORPORAT A，RODRIGUEZ-ITURBE I. Changes in rainfall seasonality in thetropics［J］. Nature Climate Change，2013，3（9）：811-815.

［10］DUTRA E，DI GIUSEPPE F，WETTERHALL F，et al. Seasonal forecasts of droughts in African basins using the Standardized Precipitation Index［J］. Hydrology and Earth System Sciences，2013，17：2359-2373.

［11］LAVERS D ， LUO L F， WOOD E F. A multiple model assessment of seasonal climate forecast skill for applications［J］. Geophysical Research Letters ，2009，36（23）. DOI：10.1029/2009GL041365.

［12］HAO Z C，SINGH V P，XIA Y L. Seasonal Drought Prediction： Advances， Challenges， and Future Prospects［J］. Reviews of Geophysics，2018，56（1）：108-141.

［13］HASTENRATH S. Recent advances in tropical climate prediction ［J］. Journal of Climate，1995，8：1519-1532.

［14］ANDERSON J，DOOL H V D，BARNSTON A，et al. Present- day capabilities of numerical and statistical models for atmosphericextratropical seasonal simulation and prediction［J］. Bulletin of the American Meteorological Society，1999，80：1349-1362.

［15］ALI M，DEO R C，MARASENI T，et al. Improving SPI-derived drought forecasts incorporating synoptic-scale climate indices in multi-phase multivariate empirical mode decomposition model hybridized with simulated annealing and kernel ridge regression algorithms［J］. Journal of Hydrology，2019，576：164-184.

［16］FENG P Y，WANG B，LUO J J，et al. Using large-scale climate drivers to forecast meteorological drought condition in growing season across the Australian wheatbelt［J］. Science of The Total Environment，2020，724. DOI：10.1016/j. scitotenv.2020.138162.

［17］施洪波，张英娟.区域气候模式 RegCMNCC对华北冬季气温和降水的预报评估［J］.气象科技，2014，42（6）：1023-1027.

［18］张人禾，殷永红，李清泉，等.利用 ARGO 资料改进 ENSO 和我国夏季降水气候预报［J］.应用气象学报，2006（5）：538-547.

［19］SCHUBERT S D，STEWART R E，WANG H L，et al. Global meteorological drought： A synthesis of cur-rent understanding with a focus on SST drivers of precipitation deficits［J］. Journal of Climate，2016，29：3989-4019.

［20］FUNK C，HOELL A，SHUKLA S，et al. Predicting East African spring droughts using Pacific and Indian Ocean sea surface temperature indices［J］. Hydrology and Earth System Sciences，2014，18（12）：4965-4978.

［21］LIU Z C，LU G H，HE H，et al. A conceptual prediction model for seasonal drought processes using atmospheric and oceanic standardized anomalies：application to regional drought processes in China［J］. Hydrology and Earth System Sciences，2018，22（1）：529-546.

［22］王兆礼，陈晓宏，李艳.珠江流域植被覆盖时空变化分析［J］.生态科学，2006，25（4）：303-307.

［23］庄少伟，左洪超，任鹏程，等.标准化降水蒸发指数在中国区域的应用［J］.气候与环境研究，2013，18（5）：617-625.

［24］MCKEE T B ，DOESKEN N J，KLEIST J. The relationship of drought frequency and duration to time scales［C］//Proceedings of the 8th Conference on Applied Climatology，California，1993.

［25］GUTTMAN N B. Comparing the palmer drought index and the standardized precipitation index［J］. Journal of the American Water Resources Association，1998，34（1）：113-121.

［26］AHN H ，MOON H ，FAZZARI M J ，et al. Classification by ensembles from random partitions of high-dimensional data［J］. Computational Statistics & Data Analysis，2007，51（12）：6166-6179.

［27］雷震.随机森林及其在遥感影像中应用研究［D］.上海：上海交通大学，2012.

（责任编辑：向 飞）