含间隙双频激励碰撞振动系统的动力学分析

马康州 卫佳 吴少培

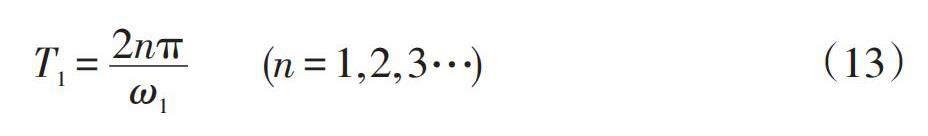
摘 要：文章研究了一类单自由度双频激励碰撞振动系统的动力学模型，建立了2个在不同频率正弦激励作用下的碰撞振动运动微分方程，给出了含间隙系统双频激励下Poincaré映射的建立方法，推导出该映射的Jacobian矩阵，从而得到相应的特征值。同时，研究了单个频率变化时对周期运动的影响，以及在一定的频率比下不同间隙和频率对周期分布的影响。进一步利用特征值研究了系统随频率变化出现的周期运动、分岔、擦边以及混沌现象，通过Poincaré映射图和相图对分岔点处的特性进行了分析。

关键词：双频激励；碰撞振动；Poincaré映射；擦边；混沌

中图分类号：O322 文献标志码：A

含间隙碰撞振动是机械系统中常见的非线性振动问题，如机械系统中弹性元件失效、弹簧与紧固件之间松动，或者装配间隙过大等因素引起的故障振动状态就是工程实际中经常发生的碰撞振动现象。

近年来，有大量文献涉及单自由度、多自由度碰撞振动系统周期运动的稳定性、分岔及混沌的研究[1-2]。乐源和谢建华[3]建立两自由度双侧约束碰撞振动系统的力学模型，推导了Poincaré映射的对称性并研究了该对称性对于周期倍化分岔、Hopf-flip分岔和Pitchfork-flip分岔具有抑制性。马召召等[4]在经典的Lyapunov指数算法和摄动理论的基础上，提出了一种可以应用于不连续系统的Lyapunov指数算法，为碰撞振动系统及不连续系统的研究提供新思路。徐洁琼等[5]分析了两自由度对称约束碰撞振动系统的退化环擦边的余维二擦边分岔，结合双擦边周期运动的存在条件和n-1-1碰撞周期运动的分岔条件，推导了此类余维二擦边分岔存在条件的表达式。刘汝逾等[6]基于含分数阶的双侧刚性约束碰撞振动模型研究系统的分岔特性，发现某参数条件下，分数阶次数减小时系统会出现音岔分岔和擦边分岔，当间隙减小时，对称不动点的稳定性发生变化并产生拟周期运动和混沌运动。Andreaus和De Angelis[7]建立双侧约束含间隙和保险杠的单自由度碰撞振动模型，分析系统的伪共振频率，通过振动台实验和数值验证方法研究谐波激励强度、保险杠刚度和间隙对于系统动力学响应的影响。吕小红等[8]基于两参数分岔分析方法，研究弹性约束碰撞振动系统在两参数平面内的擦边分岔和滑动分岔，揭示了切换滑动、多滑动和余维二滑动分岔等非光滑分岔行为。Chong等[9]讨论了单自由度碰撞振动系统各参数对系统动力学的影响，运用胞映射方法研究系统的内部激变和边界激变这两种分岔对系统动力学行为的影响。Shen等[10]通过最大李雅普诺夫指数、相位灵敏度指数和功率谱来表征奇异非混沌吸引子，在不同初始参数下，研究了拟周期的受迫系统中共存的奇异非混沌吸引子的共存特性。

工程领域中的诸多机械设备、装置的设计或运行过程中也体现了碰撞振动的原理。伍新等[11]基于Neimark-Sacker分岔理论，使用显式临界准则设计振动落砂机的参数，使系统产生拟周期运动。李国芳等[12]以一类含干摩擦的无足自驱动系统为研究对象，分析摩擦比、间隙、刚度比和质量比对系统运动特性的影响，为复杂环境中无足自驱动系统的设计提供理论依据。王乙坤等[13]构建简支输流管与刚性间隙约束的碰撞振动模型，探讨了约束间隙和恢复系数对系统动态响应的影响，同时发现了输流管刚性碰撞时的黏滑现象。张瑜等[14]考虑表面粗糙度、煤粉层的影响，建立刨头-滑架体间三维接触碰撞模型，分析系统碰撞动态特性，发现恢复系数与碰撞振动幅值、摆角振动持续时间、碰撞力和碰撞次数成正相关。蒲玉学等[15]建立机械臂与非合作碰撞物的碰撞过程动力学模型，提出了模糊策略与无模型自适应控制相结合的控制方法，为空间机械臂的碰撞问题提供理论依据。

在实际问题中，系统所受到的激励多数不是单一稳定的激励，比如多转子传动系统，由于偏质心的存在，在不同的转速下产生不同频率的振动。采用瞬时冲击法，在碰撞过程中考虑了能量的损失，利用恢复系数法计算碰撞前后速度之间的关系。建立了考虑双频激励振动系统的Poincaré映射，推导出了映射的 Jacobian 矩阵，并得到相应的特征值。进一步研究了系统随参数变化出现的周期运动的稳定性、分岔及混沌，通过Poincaré映射图、相图对分岔点处的特性进行了分析，利用特征值的穿越过程对“擦边”现象进行了研究。

1 动力学模型及其运动方程

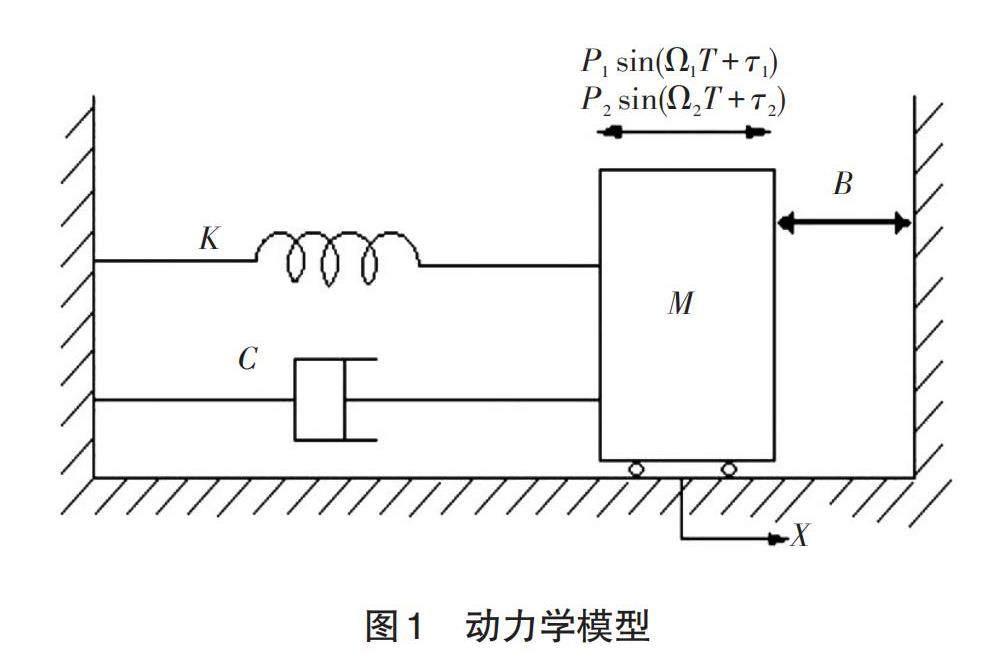
图1是一个在双频激励下的单自由度非光滑系统的力学模型，在实际工程中许多含间隙的机械系统可以抽象为该类模型进行研究。该模型由振子M 、线性弹簧K和阻尼器C组成。振子M由刚度为K的线性弹簧和阻尼系数为C的线性阻尼器联结于支承，并受到双频激励 P 1 sin（Ω 1 T+τ 1 ） 和 P 2 sin（Ω 2 T+τ 2 ） 的作用。当振子M的位移等于间隙B时，振子M与刚性约束面发生碰撞，改变速度方向后，又以新的初值运动，然后再次与约束面碰撞，如此往复。设力学模型中的阻尼是Rayleigh 型比例阻尼，碰撞过程中的能量损失由碰撞恢复系数R确定，碰撞持续时间略去不计，水平面为光滑的平面。

相邻两次碰撞之间，系统的运动微分方程为：

质块 M 的冲击方程为：式中：X?- 和X?+ 分别表示质块M与刚性约束A碰撞前后的瞬时速度。

对图1所示系统进行无量纲处理，取无量纲

运动微分方程（1）和（2）的无量纲形式可以由公式（3）和（4）表示。

当质量块M相邻两次碰撞之间运动时，利用微分求解推导微分方程的解可得：

式中 x 1 （t） 和 x 2 （t） 分别为：

式中： a 和 b 由运动的初始条件决定，令 x（0）=x 0 ，x?（0）=v 0 ，τ 1 =τ 10 ，τ 2 =τ 20 为初始条件，可得：

2 建立Poincaré映射

根据式（5）可知，随着时间t增加，微分方程解的前一部分 e-ηt[]acos（ω d t）+bsin（ω d t） 趋向零。后一部分 x 1 （t）+x 2 （t） 是系统的稳态值。现在讨论 ω 1 和 ω 2满足关系 ω 1 =iω 2 ，其中 i 为正整数，当 x 1 （t）+x 2 （t） 中的 x 1 （t） 为稳定状态，即相位 τ 1 为定值，此时 x 1 （t） 的周期由公式（13）表示为：

化简可得公式（14）：

由此当 ω 1 =iω 2 时， T 1 也为 x 2 （t） 的周期，所以 τ 2 也为定值。只需讨论 τ 1 在系统的时间历程中的稳定性。

选取 σ= { } （x?，θ）∈R2×S，x=b 作为Poincaré截面，其中θ=ω 1 t，建立Poincaré映射。取系统不动点为质量块M与右侧约束面第一次接触后的瞬时，其坐标表达式为 （x?，θ） 。该表达式的物理意义是将Poincaré截面选刚性约束面，则周期运动的稳定性问题转化为Poincaré映射线性化矩阵在不动点处的特征值问题。根据接触过程可以将Poincaré映射分为2个阶段：P 1 表示质量块M和右侧碰撞面碰撞接触阶段；P 2表示质量块M与右碰撞面脱离阶段。

令 DP 1 ，DP 2 分别代表 P 1 ，P 2 的映射矩阵，并设：

则Poincaré映射可表示为：

再由式（17）得到图1所示系统Poincaré映射的Jacobian矩阵DP. Jacobian 矩阵的特征值决定了相应周期运动的稳定性。如果矩阵的所有特征值都位于单位圆内，那么相应的周期运动是稳定的。当线性化矩阵特征值的最大模位于单位圆上时，根据这样特征值的数量以及它们在单位圆上的位置，会发生各种不同的分岔现象。当仅有1个特征根为λ=1，将产生鞍结分岔；若仅有1个特征根为 λ=-1 ，则出现倍周期分岔。若有一对共轭特征值的模 | | λ =1 ，而其余的特征值都位于单位圆周内，系统的周期运动将发生Hopf分岔。

3 数值模拟

3.1 单个频率变化

选取图1所示系统的参数：b=0.1，R=0.8，f 1 =0.2，f 2 =0.8，x 0 =0.1，v 0 =0.001。图2为 ω 2 取不同的值， ω 1在1.2～6.5变化时，质量块M在Poincaré截面处的速度分岔图。

由图2看出沿着 ω 2 轴方向变化时，随着 ω 2 增加，质量块的速度波动中心逐渐增大，波动的幅度没有太大的变化。沿着 ω 1 轴方向的变化，速度会沿着一个 v 值上下波动，呈现出衰减式的周期变化。下面具体讨论 ω 2 =1.5 和 ω 2 =2 时系统周期运动情况。

图3对应 ω 2 =1.5 时系统分岔图，可以看出，质量块的速度在 ω 1 轴上，以周期为1.5呈现周期衰减变化，在 ω 1 等于 ω 2 的2倍和3倍处为周期一运动，在2.5倍处为周期二运动。图4中分别为 ω 1 =2ω 2 ，ω 1 =2.5ω 2 ， ω 1 =3ω 2 和 ω 1 =3.745 的相图。

当 ω 2 =1.5 ，取不同的 ω 1 做系统的Poincaré图，如图5所示。图中（a）为 ω 1 =（7/4）ω 2 ，系统表现为周期四运动；（b）为 ω 1 =（15/8）ω 2 ，系统表现为周期八运动；（c）为 ω 1 =（31/16）ω 2 ，系统表现为周期十六运动；（d）为 ω 1 =（（2^10-1）/2^9）ω 2 ，系统为拟周期运动。

图6为ω 2 =2时系统分岔图，可以看出与ω 2 =1.5相比，由两个小波峰变成了一个，同样有周期衰减变化出现，此时系统周期为2。在ω 1 =3.983处出现小波峰。图7分别为 ω 1 =2ω 2 ， ω 1 =2.5ω 2 ， ω 1 =3ω 2 和ω 1 =3.983 的相图。

当 ω 2 =2.0 ，取不同的 ω 1 做系统的Poincaré图，如图8所示。图中（a）为 ω 1 =（7/4）ω 2 ，系统表现为周期四运动；（b）为 ω 1 =（15/8）ω 2 ，系统为周期八运动；（c）为 ω 1 =（31/16）ω 2 ，系统为周期十六运动；（d）为ω 1 =（（2^10-1）/2^9）ω 2 ，系统表现为拟周期运动。

由上面2个例子可以得出当 ω 2 为一个固定值时，随着 ω 1 的变化，质量块的速度会有周期衰减的规律，其中衰减周期为ω 2 ，同时当频率 ω 1 是 ω 2 的m+（2^n-1）/2^（n-1） 倍时，系统表现为周期 2^（n-1）运动，其中 （m=0，1，2，3，4….n=1，2，3，4…） 。

3.2 双频激励成比例变化

图9为系统频率比i=2，各参数取：b=0.1，R=0.8，f 1 =0.2，f 2 =0.8，x 0 =0.1，v 0 =0.001， ω 1 在5.5到6.5变化时，系统局部分岔图。随着参数 ω 1 减小会出现逆倍化分岔，当 ω 1 <6.174 0 时，从周期一运动退化成稳定的周期二运动。随着 ω 1 的进一步递减，在 ω 1 <5.954 3时进入周期四运动。参数 ω 1 继续递减，在 ω 1 =5.887 68时系统运动进入到混沌状态。

当 ω 1 ∈[6.17，6.20]时，系统Jacobian矩阵特征值的变化如图10所示，同时可以根据表1所表示的特征值的大小来判断不动点的性质。当 ω 1 <6.173 9 时，特征值的绝对值小于1，系统具有稳定的周期一运动。在 ω 1 =6.173 9 时特征值为-1.003 97，系统Poi?ncaré图和相图如图11所示； ω 1 =6.174 0 时特征值为-0.998 91，系统Poincaré图和相图如图12所示，故在此两点间发生倍化分岔，系统由稳定的周期二运动进入周期一运动。

当 ω 1 ∈[5.95，5.96]时，系统Jacobian矩阵特征值随 ω 1 变化趋势如图13所示。在 ω 1 =5.954 3 时由稳定的周期二运动进入周期四运动，此处发生倍化分岔，在系统 ω 1 =5.940 处的Poincaré图和相图如图14所示。

如图15所示，当 ω 1 进一步减小，可以看出在ω 1 =5.887 68 与 ω 1 =5.887 69 之间系统从周期四运动突然进入到混沌状态，相应系统的特征值从单位圆内跳出。由图16（a）和图16（b）看出有擦边现象的出现，在“擦边”前后当质块的运动周期和穿越Poincaré截面的次数都发生变化，使得系统从周期运动突变到混沌运动。由图16可以看出其演变过程。

3.3 频率成比例的双激励和间隙对系统的影响

分岔图是机械系统中参数选择的重要依据。对实际参数的选择往往是多元化，二维分岔图只能表现出在单个参数下的工作性能。系统在满足一定的频率比的情况下，频率和间隙如何选择才能使振子达到理想的工作状态。采用三维分岔图两维坐标分别为频率和间隙，第三维以颜色的形式表现系统的性能。

图17和图18分别为频率比i取2和3时系统周期运动的分布图，间隙b取不同的值可以看出系统的周期分布，图17、图18中的标注 pi（i=1，2，3，4，5，6）代表周期i。

4 结论

文章以单自由度双频激励碰撞振动系统为研究对象，给出了系统的Poincaré映射建立方法，推导出了其对应的Jacobian矩阵，从而得到相应的特征值。利用特征值的穿越单位圆过程，相图和Poin?caré 截面图以及分岔图分析2个频率之间不同关系时系统的特性。

（1）单个频率变化时， ω 2 取不同值，随着 ω 2 增加，质量块的速度波动中心逐渐增大。 ω 2 取定值，ω 1 在一定范围内变化时，质量块的速度会有周期衰减的规律，其中衰减周期为 ω 2 ，同时当频率 ω 1 为ω 2 的 m+（2^n-1）/2^（n-1） 倍时，系统表现为周期2^（n-1） 运动，其中（m=0，1，2，3，….n=1，2，3，4…）。

（2）双频激励成比例为2变化时，系统的演化过程中，有一个特征值在-1处穿越单位圆，其余位于单位圆内，此时产生倍化分岔。在“擦边”处会有特征值从单位圆内跳出，出现非光滑分岔，由周期运动直接通向混沌。

（3）根据机械设计参数多元化的特点，采用三维分岔图，两维坐标分别为系统参数，第三维以颜色的形式表现系统的运动特性，为含间隙的碰撞振动机械系统的参数设计提供理论依据。

参考文献：

[1]丁旺才，谢建华. 碰撞振动系统分岔与混沌的研究进展[J].力学进展，2005（4）：513-524.

[2]金栋平，胡海岩. 碰撞振动与控制[M]. 北京：科学出版社，2005.

[3]乐源，谢建华. 两自由度碰撞振动系统的Poincaré映射的对称性及分岔[J]. 振动工程学报，2008（4）：376-380.

[4]马召召，杨庆超，周瑞平. 一种基于摄动理论的不连续系统Lyapunov指数算法[J]. 物理学报，2021，70（24）：68-75.

[5]徐洁琼，陈慧莹，伍帅，等. 一类对称约束碰振系统的余维二擦边分岔的存在条件[J]. 振动与冲击，2022，41（5）：273-279.

[6]刘汝逾，牛江川，申永军，等. 分数阶单自由度线性振子双侧对称碰撞振动分析[J]. 振动与冲击，2021，40（16）：20-28.

[7]Andreaus U，De Angelis M. Experimental and numerical dynamic response of a SDOF vibro-impact system with double gaps and bumpers under harmonic excitation[J].International Journal of Dynamics and Control，2019，7（4）：1278-1292.

[8]吕小红，张开成，朱喜锋，等. 两自由度碰撞振动系统的两参数非光滑分岔[J]. 振动工程学报，2023，36（1）：107-115.

[9]Chong A S E，Yue Y，Pavlovskaia E，et al. Global dynam?ics of a harmonically excited oscillator with a play：Nu?merical studies[J]. International Journal of Non-Linear Mechanics，2017，94（Sep.）：98-108.

[10]Shen Y，Zhang Y，Jafari S. Coexistence of strange noncha?otic attractors in a quasiperiodically forced dynamical map[J]. International Journal of Bifurcation and Chaos in Applied Sciences and Engineering，2020，30（13）：2050183.

[11]伍新，文桂林，何莉萍，等. 振动落砂机系统的拟周期碰撞设计[J]. 湖南大学学报（自然科学版），2016，43（4）：38-43.

[12]李国芳，俞力洋，丁旺才，等. 一类无足自驱动系统的运动特性分析[J]. 振动与冲击，2020，39（14）：9-16.

[13]王乙坤，王琳，倪樵，等. 具有刚性间隙约束输流管的碰撞振动[J]. 力学学报，2020，52（5）：1498-1508.

[14]张瑜，王倩，陈洪月，等. 含煤粉层的刨头-滑架体三维粗糙接触碰撞特性研究[J]. 振动与冲击，2022，41（8）：250-259.

[15]浦玉学，周润闰，陈演，等. 空间机械臂碰撞过程的模糊无模型自适应振动控制[J]. 振动与冲击，2023，42（19）：14-21.

Dynamics Analysis of Vibro-impact System with Double-frequency Excitation and Clearance

MA Kangzhou，WEI Jia，WU Shaopei

（Lanzhou Jiaotong University，Lanzhou Gansu 730070，China）

Abstract： The paper mainly studies a kind of single-degree impacting dynamical model with double-frequency excitation，establishes the equation of vibro-impact with double-frequency.The Poincaré map of system is estab?lished to deduce the Jacobian matrix and the corresponding eigenvalues. It also studies the influence of the single-frequency change to periodic motion. And under a certain ratio of frequency， it studies the influence of frequency and clearance to the periodic distribution. The paper further uses the eigenvalues to study the phenomenon of peri?odic motion， bifurcation，rubbing edge and chaotic motion，and analyzes the characteristics of the bifurcation points through the Poincare map diagram and the phase diagram.

Key words： double-frequency excitation; vibro-impact; Poincaré map; grazing; chaos