类比推理 创新求解 提升素养

陶汉斌

［摘 要］类比是一种极具启发性、创造性和灵活性的推理方法。每当学生缺乏可靠论证的思路时，类比这一方法往往能使他们厘清思路，指引他们进行深度学习。2024年1月浙江选考物理第20题通过类比设置问题情境，情境设计既熟悉又新颖；巧妙借用光学知识类比电磁场知识，通过调控磁场或电场实现质子束的“反射”和“折射”；从知识、方法到能力，问题的设计由易到难，全面考查了学生的综合分析能力。

［关键词］类比；情境；反射；折射；电磁场

［中图分类号］    G633.7        ［文献标识码］    A        ［文章编号］    1674-6058（2024）08-0040-03

类比是一种逻辑推理形式，是一种极具启发性、创造性和灵活性的推理方法。当物理学研究陷入困境时，通过类比方法往往能打开一片新天地。每当学生缺乏可靠论证的思路时，类比这一方法往往能使学生厘清思路，指引他们进行深度学习。2024年1月浙江选考物理第20题通过类比设置问题情境，类比光学中的反射和折射现象，用磁场或电场调控实现质子束的“反射”和“折射”。同时，由易到难设计问题，全面考查学生的综合分析能力。

一、试题呈现

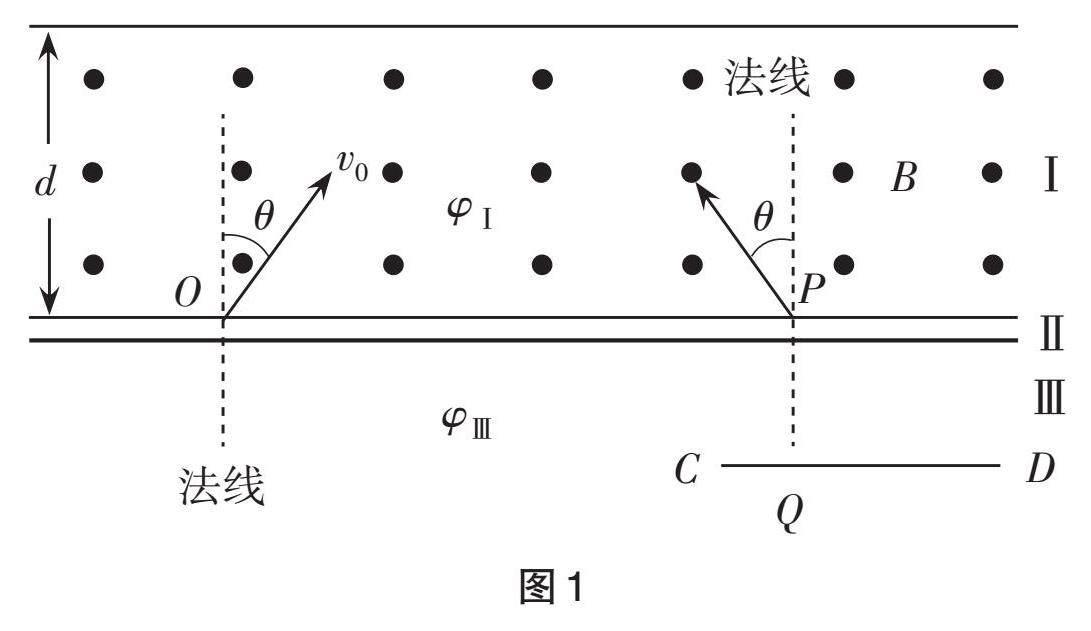
类似光学中的反射和折射现象，用磁场或电场调控也能实现质子束的“反射”和“折射”。如图1所示，在竖直平面内有三个平行区域Ⅰ、Ⅱ和Ⅲ。Ⅰ区宽度为[d]，存在磁感应强度大小为[B]、方向垂直平面向外的匀强磁场，Ⅱ区的宽度很小。Ⅰ区和Ⅲ区电势处处相等，分别为[φⅠ]和[φⅢ]，其电势差[U=φⅠ-φⅢ]。一束质量为[m]、电荷量为[e]的质子从[O]点以入射角[θ]射向Ⅰ区，在[P]点以出射角[θ]射出，实现“反射”；质子束从[P]点以入射角[θ]射入Ⅱ区，经Ⅱ区“折射”进入Ⅲ区，其出射方向与法线夹角为“折射”角。已知质子仅在平面内运动，单位时间发射的质子数为[N]，初速度为[v0]，不计质子重力，不考虑质子间相互作用以及质子对磁场和电势分布的影响。

（1）若不同角度射向磁场的质子都能实现“反射”，求[d]的最小值；

（2）若[U=mv202e]，求“折射率”n（入射角正弦与折射角正弦的比值）；

（3）计算说明如何调控电场，实现质子束从[P]点进入Ⅱ区发生“全反射”（即质子束全部返回Ⅰ区）；

（4）在[P]点下方距离[3mv0Be]处水平放置一长为[4mv0Be]的探测板[CQD] （[Q]在[P]的正下方）， [CQ]长为[mv0Be]，质子打在探测板上即被吸收中和。若还有另一相同质子束，与原质子束关于法线左右对称，同时从[O]点射入Ⅰ区，且[θ=30°]，求探测板受到竖直方向力[F]的大小与[U]之间的关系。

二、考情分析

此题利用学生熟悉的光学中的反射和折射现象，类比推理电磁场中的“反射”和“折射”，设计巧妙新颖。很多学生以为这是一道光学题，但它只是利用光学中的反射场景类比质子在磁场中的匀速圆周运动；利用光学中的全反射情境类比质子在电场中斜抛后运动到最高点又在电场中返回（逆平抛）；以光学中熟悉的折射类比质子穿越电场的斜抛运动。本题的最后一个问题涉及利用临界条件进行分析的分段函数，常考常新，非常精彩。

三、详细解答

（1）在磁场中的匀速圆周运动——类比反射

质子射入磁场后在磁场中做匀速圆周运动，当竖直方向上射出的质子恰好打到上极板时有：

[Bev0=mv20r]

[2r=d]

[d=2mv0Be]

（2）在电场中的斜抛运动——类比折射

质子束从[P]点以入射角[θ]射入Ⅱ区中的电场，在电场中做斜抛运动，有[U=mv202e]，设质子射出Ⅱ区时的速度为[v]，由动能定理可得：

[eU=12mv2-12mv20]

解得[v=2v0]

射出时质子的水平速度为[vx=v0sinθ]

通过类比可得折射率为[n=sinθv0sinθ2v0=2]

（3）在电场中做减速运动后返回——类比全反射

质子从[P]点射入时，设电场的间距为[L]，在质子刚好在Ⅱ区减速到0时，应用运动学公式有：

[0-（v0cosθ）2=2U0emLL]

[U0=-mv02cos2θ2e]

即当  [U≤-mv02cos2θ2e] 时发生“全反射”

（4）利用临界值求解分段函数——常规考点

第（4）问需要根据隐含条件进行分析，判断临界边际，多个角度讨论各种情况，物理模型的构建与数学处理有一定难度。我们可利用临界值进行求解，由于[θ=30°]，质子恰好不能进入Ⅲ区的电压为[U1]，在竖直方向上应用运动学公式有：

[0-（v0cos30°）2=2U1emLL]

[U1=-3mv208e]

考虑探测板上的C点，当电压为[U2=0]时，由于[tan30°=CQPQ=33]，左侧的质子经过Ⅱ区时做匀速直线运动，恰好打在C点。

考虑探测板上的D点，当电压为[U3]时恰好打在D点，右侧的质子经过Ⅱ区，由动能定理得：

[eU3=12mv0sin30°cos30°2-12mv20]

[U3=-mv203e]

①当[U<-mv203e]时，[F=0]

②当[-mv203e≤U<0]时，左侧质子打不到探测板，设打到探测板的右侧质子的速度为[v]，则有：

[eU=12mv2-12mv20]

解得[v=v20+2eUm]

而右侧质子的水平速度为[vx=v0sin30°=0.5v0]

因此打到探测板时右侧质子的竖直速度为[vy=34v20+2eUm]

竖直方向应用动量定理有：

[F·Δt=N·Δtm34v20+2eUm]

解得竖直方向上的力[F=Nm34v20+2eUm]

③当电压[U>0]，左、右两侧质子都打到探测板，同理可得[F=2Nm34v20+2eUm]

综上所述，探测板受到竖直方向上的力[F]的大小与电压[U]之间的关系如下：

当[U<-mv203e]时，[F=0]

当[-mv203e≤U<0]时，[F=Nm34v20+2eUm]

当[U>0]时，[F=2Nm34v20+2eUm]

四、教学反思

此题学生普遍反映难度很大，这是因为他们缺乏类比推理的能力。通过此题，学生知道原来类比光学中的反射和折射现象，通过磁场或电场调控也可以实现质子束的“反射”和“折射”。类比是一种逻辑推理形式，是一种极具启发性、创造性和灵活性的推理方法。应用两种物理现象和两种物理规律之间的相似或相同，而推出其他方面也相似或相同的方法就是类比法，类比法贯穿物理学的研究过程。

类比法往往能指引学生进行深度学习。比如“电场”这一章中库仑定律与万有引力定律的类比，电场与重力场的类比，重力场中的平抛与电场中的类平抛的类比。

其中，万有引力定律与库仑定律的类比如表1所示。

电场与重力场的类比如表2所示。

学生应该具有这样的意识——考试中的失分都应该归结到自身素养欠缺上，而素养除物理观念、科学探究、科学推理、科学论证、模型建构外［1］，还包括对自身思维过程进行的监控——“对自己的思维方式、思维过程进行质疑”。教师在向学生传授知识的同时，还应该引导学生归纳总结重要的科学研究方法，以更好地培养学生的科学研究能力。科学研究是学生终身受用的本领。只有让学生积极主动地开展科学研究，才能更好地提升学生的学科核心素养。

［   参   考   文   献   ］

［1］  梁旭.基于核心素养的学·教·评：浙江省近几年高中物理教学的探索与实践［J］.中学物理，2021（21）：2-6.

（责任编辑 黄春香）