迂曲裂缝内支撑剂运移数值模拟

胡晓东 张鹏天 周福建 李昕桐 白亚超 陈超

摘要：水力压裂后，储层形成较多的迂曲裂缝，支撑剂在迂曲裂缝中的运移和铺置规律尚不明确，在稠密颗粒流模型的基础上耦合颗粒物料仿真软件，模拟迂曲角度、支撑剂尺寸、注入速率、携砂液密度和支撑剂密度对迂曲裂缝中支撑剂运移和砂堵的影响。结果表明：大多支撑剂会堆积在裂缝第一转折角处，迂曲角度的变化会显著影响支撑剂的运移和砂堵的发生，迂曲角度大，容易发生砂堵且砂堵程度严重；密度大和粒径小的支撑剂发生砂堵时会形成致密的支撑剂堆积，加剧砂堵程度；注入速率大，支撑剂在裂缝中运移距离较远，但注入速度和携砂液密度的增加，会加剧砂堵程度。

关键词：迂曲裂缝； 支撑剂运移； 砂堵预测； 数值模拟

中图分类号：TE 357.12   文献标志码：A

文章编号：1673-5005（2024）03-0111-08   doi：10.3969/j.issn.1673-5005.2024.03.012

Numerical simulation of proppant transport in tortuous fractures

HU Xiaodong1，2， ZHANG Pengtian1，2， ZHOU Fujian1，2， LI Xintong1，2， BAI Yachao1，2， CHEN Chao1，2

（1.State Key Laboratory of Petroleum Resources and Engineering， Beijing 102249， China;2.Unconventional Petroleum Research Institute， China University of Petroleum（Beijing）， Beijing 102249， China）

Abstract： After hydraulic fracturing， numerous tortuous fractures can be generated and formed in the reservoir， and the migration and distribution behavior of proppants in these tortuous fractures is not clear. In this study， in coupling with a simulation software of granular materials， a dense particle flow model was proposed to simulate the effects of tortuosity angle， proppant size， injection rate， carrying fluid density and proppant density on the migration of proppants and sand plugging in tortuous fractures. The results show that most proppants can accumulate at the location of first turning angle of the fracture. The variation in tortuosity angle can significantly affect the migration of proppants and the occurrence of sand plugging， with a higher tortuosity angle leading to more severe sand plugging. Proppants with higher density and smaller particle size tend to form dense proppant accumulation during sand plugging， exacerbating the severity of sand plugging. Higher injection rates can result in longer migration distances of proppants in the fracture， but increasing injection velocity and carrying fluid density can exacerbate the severity of sand plugging.

Keywords： tortuous fractures; proppant transport; sand plugging predictions; numerical simulation

近年来水力压裂已经成为非常规增产改造的重要手段，支撑剂在裂缝中的运移和分布是水力压裂的一个重要部分，由于地层的非均质性，水力压裂形成许多迂曲裂缝，在支撑剂注入过程不能参照平面平行裂缝中支撑剂运移规律，因此研究支撑剂在迂曲裂缝中的运移十分关键［1-3］。水力压裂形成的裂缝形态复杂，如果泵注设计不合理，压裂施工过程中就会存在砂堵风险，支撑剂在裂缝中的堆积状态决定了裂缝导流能力［4］，最终会影响采收率。通过调研国内外相关研究，发现目前对迂曲裂缝中支撑剂运移的研究较少，对迂曲裂缝内运移过程砂堵风险的讨论鲜有提及，仅有的一些研究主要采用试验的方法和Fluent数值模拟两种途径。然而，由于试验场地限制和试验条件难以控制且大多数的试验适用于平直裂缝，试验结果的准确性并不理想；采用Fluent进行模拟，无法精确模拟支撑剂颗粒的运移，无法进一步进行砂堵的模拟。针对上述问题，笔者采用Fluent和EDEM耦合［5］的方法进行模拟研究。稠密离散相模型（DDPM）是专门用来模拟稠密颗粒流的模型，可以理解为简化了的离散元方法（DEM）［6］，该模型考虑了颗粒的空隙率以及碰撞，但是对于碰撞的计算进行了简化，不是计算真实的碰撞过程，因此为了更加真实地模拟支撑剂的碰撞过程，笔者在DDPM模型的基础上耦合EDEM软件来模拟支撑剂的运移过程，直观地观察支撑剂的运移过程，分析迂曲裂缝内支撑剂运移的影响因素以及对应工况下裂缝入口压力特征，为砂堵预测预警提供有效建议。

1 模型的开发与验证

通过调研以前的支撑剂运移数值模拟研究，发现数值模型主要分为欧拉-拉格朗日模型和欧拉-欧拉模型两种类型。欧拉-拉格朗日模型［7］将流体看作连续相，颗粒看作离散相，用欧拉法处理流体运动，拉格朗日方法计算颗粒运动轨迹。欧拉-拉格朗日模型计算结果精确，但耗费时间较长。欧拉-欧拉模型把流体和颗粒看成一种混合的连续相进行计算，通过欧拉-欧拉模型可以快速获得模拟结果。但是欧拉-欧拉模型把固液作为一个整体计算，无法得到颗粒的运动轨迹。

Larry等［8］使用透明测试仪研究了水基冻胶压裂液中的支撑剂运移规律，但由于试验方案设计不足，试验没有取得成功。Nolte［9］提出了一种广泛用于支撑剂运移研究的方法。在这个方法中定义了流体效率，它是用裂缝体积除以注入流体体积，其目的是准确且较为简单地研究支撑剂运移过程。然而，上述两个模型都只适用于使用高黏度的携砂液且不考虑支撑剂沉降过程。Siddhamshetty等［10］提出了一个用于页岩中低黏度流体的支撑剂运移模型，该模型中的支撑剂运移是由欧拉-欧拉模型模拟的。由于支撑剂被认为是连续相，其间的相互作用如碰撞和分散不能被准确模拟。因此使用欧拉-欧拉模型进行支撑剂运移设计不准确。

在欧拉-拉格朗日模型的基础上设计一个实验室规模的支撑剂运移模型。假设：携砂液是牛顿流体；携砂液在裂缝中的滤失忽略不计。

1.1 数学模型

本文中的模型是基于稠密离散相法DDPM［11］建立的。DDPM模型是欧拉-拉格朗日模型的一个子类型模型，被广泛用于石油工程中的支撑剂运移模拟。为了更加真实地描述和模拟支撑剂在迂曲裂缝的运移过程，通过DDPM模型接口建立了CFD-DEM耦合模型。CFD-DEM耦合模型可以直观准确地模拟支撑剂运移问题。

流场采用CFD方法求解，流体流动过程方程式［12］为

u=0，（1）

ρut+ρ（u）u=-p+μ2.（2）

式中，ρ为流体密度，kg/m3；u为流体速度，m/s；p为流体压力，Pa；

μ为流体黏度，Pa·s。

式（1）、（2）称为纳维-斯托克斯方程，满足了流体的质量和动量守恒。颗粒运动采用DEM方法求解。该方法将牛顿第二定律应用于单个粒子轨迹的计算，该轨迹由作用于每个粒子的力和力矩的总和产生。粒子运动方程［13］为

mp=dvpdt=Fp，f+Fp，p+Fp，w+Fb，（3）

Ip=dωpdt=rpFt.（4）

式中，mp为粒子质量，kg；vp为粒子速度，m/s；t为时间，s；

Fp，f为周围流体施加在粒子上的力，N；Fp，p为粒子与粒子间接触力，N；

Fp，w为粒子与壁面间接触力，N；Fb为粒子体积力，N；rp为粒子半径，m；Ft为作用在粒子上的切向力，N；Ip为粒子的转动惯量，对于球形粒子， Ip为（2/5）mpr2p，kg·m2 ；wp为粒子角速度，s-1。

根据Hertz的法向接触理论［14］和Mindin等的切向接触理论［15］，Fp，p由法向力和切向力组合表示为

Fp，p=（knδn-γnΔup）+（ktδt-γtΔut）.（5）

式中，k为弹力系数，N/m；δ为重叠高度，m；γ为阻尼系数，N·s/m；Δu为接触点处的相对速度，m/s;下标n和t分别表示法向和切向。弹力系数和阻尼系数可以根据粒子材料特性得出［16］。

流体作用在粒子上的力［17］表示为

Fp，f=∫（-p+μ2u）dΩs.（6）

式中，Ωs为粒子域。

由于携砂液携带支撑剂在裂缝中的流动形态为湍流流态，因此本文中全部采用标准K-E模型［18］，其中K为紊流脉动动能，K越大表明紊流脉动长度和时间尺度越大；E为紊流脉动动量的耗散率，E越大代表紊流脉动长度和时间尺度越小。

1.2 物理模型

采用三维迂曲裂缝模型来模拟迂曲裂缝中的支撑剂运移过程。建立一条长0.4 m、高0.1 m和宽0.002 m、迂曲角度为45°的裂缝中固液两相流模型，利用Fluent和EDEM耦合的方法对迂曲裂缝中的支撑剂运移和砂堵预测进行模拟。图1为基本案例模型。

1.3 模型验证

首先建立一个三维垂直平面裂缝模型，用于模型验证。裂缝的长度、高度和宽度分别为0.381、0.0762和0.002 m，网格总数为10000，支撑剂粒径、质量分数和密度分别为0.6 mm、1.3%和2650 kg/m3，携砂液密度和黏度分别为1000 kg/m3和0.001 Pa·s，注入速度为0.3 m/s。图2为裂缝长度和高度方向的网格和几何形状。在模拟中使用了速度入口和压力出口。假设为湍流流态，压力-速度耦合与校正采用SIMPLE算法［19］。动量和体积分数的空间离散化处理采用QUICK方案 ［20］。为了便于收敛，湍流动能方程和湍流耗散率系数方程采用一阶迎风格式［21］。

通过Tong等［22］的试验数据和Hu等［23］的模拟结果来验证本文的模型。比较注入速度为0.3 m/s时的支撑剂分布情况，结果如图3所示，可以看到该模型中支撑剂床的分布与试验数据相似。为了更加清楚地比较结果，采用无量纲支撑剂运移长度（支撑剂运移长度与裂缝总长度之比，DPBL）和无量纲支撑剂床层高度（最大支撑剂床层高度和总裂缝高度的比，DPBH）［23］。相同条件下，Tong等、Hu等［23］和本文中无量纲支撑剂运移长度分别为86.27%、95.10%和90.20%，无量纲支撑剂床层高度分别为50%、45%和57.14%。本文模型结果和文献［22］试验结果及文献［23］模拟结果之间的DPBL的最大误差为4.9%，DPBH的最大误差为12.14%，说明本文的模型与试验结果有合理的匹配。本文中模型与Tong等的试验误差主要是由于试验中的分支缝，试验中存在一个旁路，这导致支撑剂运移到二级裂缝中；与Hu等的模拟结果存在误差的原因在于本文的颗粒运移计算采用EDEM软件，而在文献［23］中的模拟，颗粒和流体都是用ANSYSFLUENT软件进行计算的。

2 数值模拟结果分析

通过数值模拟的方法研究迂曲角度、支撑剂尺寸、注入速率、支撑剂密度、裂缝宽度和支撑剂密度对迂曲裂缝中支撑剂沉降和砂堵的影响。

2.1 基本案例

基本案例，裂缝的长度、高度和宽度分别为0.4、0.1和0.002 m，支撑剂粒径、质量分数和密度分别为0.6 mm、1.3%和2650 kg/m3，携砂液密度和黏度分别为1000 kg/m3和0.001 Pa·s，注入速度为0.3 m/s。图4为支撑剂运移与砂堵情况。由图4可以看出，携砂液携带的支撑剂最初倾向于在第一段裂缝的下部区域沉淀并形成支撑剂床。随着支撑剂的不断注入，支撑剂在裂缝宽度变窄时，首先在第一转折角形成支撑剂堆积，随支撑剂不断增多最终形成密实的支撑剂堆积，阻碍后进入的支撑剂运移，这时入口压力激增形成砂堵。

2.2 迂曲角度对支撑剂运移和砂堵的影响

图5为不同迂曲角度下注入时间为2 s时支撑剂的运移和砂堵状况。在迂曲角度为0°时，支撑剂运移距离较远，由于整个裂缝宽度相同，支撑剂的堆积面是一个平稳的曲线面，同时在压力曲线上，裂缝的入口压力没有剧烈变化，因而没有发生砂堵现象；当迂曲角度增到15°时，可以明显地看到在两个裂缝转折处支撑剂堆积呈现翘角的状态，这是由于在裂缝转折处裂缝变窄，流体与支撑剂的流动方向和速度发生改变，但其裂缝入口压力也没有剧烈变化，未出现砂堵现象；当迂曲角度增到30°和45°时，支撑剂大部分堆积在第一段裂缝内且在第一个转折处出现翘角，翘角的出现阻碍了支撑剂的运移，同时裂缝入口压力都在2 s内的某一时刻发生激增，出现了砂堵现象。

在迂曲角度为30°和45°的裂缝中，2 s内发生了砂堵现象。通过计算可得45°迂曲裂缝入口压力突变时间和入口压力峰值时间比30°迂曲裂缝的分别提前了34%和29%，而入口压力峰值却只比30°迂曲裂缝的高了1.7%。这说明迂曲角度会影响砂堵形成的时间，对支撑剂封堵裂缝的严重程度影响较小。迂曲角度越小，支撑剂运移长度越长，且越不容易形成砂堵。

2.3 注入速率对支撑剂运移和砂堵的影响

在压裂施工过程中，注入速率是影响支撑剂运移的重要参数。不同注入速率的支撑剂运移与砂堵情况如图6所示。

当注入速率为0.1 m/s时，可以看出在2 s时，支撑剂的运移尚未到达裂缝第一转折角处，支撑剂主要堆积在注入口附近，其裂缝入口压力在2 s内没有激增变化；注入速率为0.2 m/s时，支撑剂已经运移到裂缝第一个转折角处，且在第一个转折角前形成了大量沉积，入口压力在2 s内也没有发生激增，说明2 s时虽然支撑剂大量堆积在第一段裂缝中，转折角处几乎被支撑剂堆满，但其入口处还可以进入流体和支撑剂，不会出现砂堵现象；注入速率为0.3和0.4 m/s时，支撑剂虽然有运移更远距离的趋势，但是裂缝发生转折，使其宽度以及流体、支撑剂运移方向和速度改变，只有极少量的支撑剂可以通过第一个裂缝转折处进入第二段裂缝内，同时堆积在转折处的支撑剂墙阻碍着后进入的流体和支撑剂。在入口压力曲线上，也可以看到0.3 和0.4 m/s的入口压力均在2 s内发生激增，即在该时刻发生了砂堵现象。注入速率为0.4 m/s的裂缝入口压力开始突变时间和入口压力峰值时间比0.3 m/s的提前了71%和73%，入口压力峰值也比0.3 m/s的提高了38%。这说明注入速率的增加在一定程度上确实可以使支撑剂运移的更远，但是当支撑剂在迂曲角前已形成堆积时，增加注入速率会提前砂堵发生的时间也会增加支撑剂封堵裂缝的严重程度。

2.4 支撑剂粒径对支撑剂运移和砂堵的影响

迂曲角度为45°，支撑剂以0.3 m/s的固定速率注入，入口支撑剂质量分数恒定为10%，不同粒径支撑剂运移和砂堵情况如图7所示。

从图7中可以看出：粒径为0.4 mm的支撑剂在通过裂缝时，只要有很少的一部分在裂缝第一个转折角处堆积就会形成砂堵；粒径为0.5 和0.6 mm的支撑剂通过裂缝时，支撑剂在2 s内也会在裂缝的第一个转折角度堆积，最终造成砂堵；粒径为0.7 mm的支撑剂通过裂缝时，支撑剂也会在第一个转折角处形成堆积，但0.7 mm的支撑剂在2 s内虽有堆积，但其未造成砂堵。同时，随着支撑剂粒径的增大，裂缝第一个转折角前形成的支撑剂堆积增多。说明支撑剂粒径越大，其形成的支撑剂堆积越不致密，其中的缝隙越容易使流体通过。粒径为0.4、0.5和0.6 mm的支撑剂入口压力都在不到2 s发生了激增，而粒径0.7 mm的支撑剂入口压力在2 s内几乎没有变化。这也说明0.4、0.5 和0.6 mm粒径的支撑剂在运移过程中都造成了砂堵，而0.7 mm粒径的支撑剂运移过程中，2 s内并未发生砂堵。同时支撑剂颗粒越小，入口压力激增的时间越靠前，迂曲裂缝越快形成砂堵，同时支撑剂粒径越小，封堵裂缝的程度越严重。

2.5 携砂液密度对支撑剂运移和砂堵的影响

图8为不同携砂液密度下发生砂堵时的情况。从图8中可以看出，当发生砂堵前一时刻，不同携砂液密度下，支撑剂沉积情况和在第一转折角前形成的支撑剂堆积几乎相同。携砂液密度为

1000、950 和900 kg/m3时入口压力先发生突变，且发生突变的时间也几乎相同，而携砂液密度为850 kg/m3时入口压力突变时间稍滞后。这说明在密度较大的携砂液里支撑剂沉降较慢，支撑剂可以更快地随携砂液到达裂缝第一转折角处，从而造成砂堵。裂缝入口处最大压力对应的携砂液密度依次为1000、950、900、850 kg/m3。在迂曲裂缝中，携砂液密度越大越容易形成砂堵且支撑剂封堵裂缝程度严重。

2.6 支撑剂密度对支撑剂运移和砂堵的影响

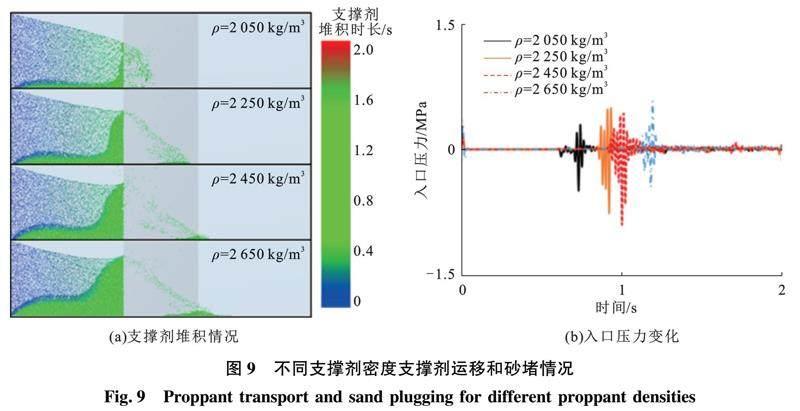
裂缝迂曲角度为45°，支撑剂以0.3 m/s的固定速率注入，入口支撑剂质量分数恒定为10%，不同支撑剂密度下支撑剂运移和砂堵情况如图9所示。

角处形成支撑剂堆积。随着支撑剂密度增大，发生砂堵时支撑剂在转折角度形成的砂堵堆积越多。这就说明支撑剂密度越小，支撑剂在运移过程中越不容易沉降，其运移到裂缝转折角处的时间也就越短，越快速地在裂缝转折角处形成支撑剂堆积，从而造成砂堵。同时，随着支撑剂密度的增大，迂曲裂缝入口压力激增的时间也在不断增大。这也说明支撑剂密度越大，形成砂堵的时间越晚，但是迂曲裂缝入口压力峰值在整体规律上却在不断增大，砂堵裂缝的程度越严重。

3 结 论

（1）支撑剂在迂曲裂缝中的运移过程中，大多数支撑剂会在第一个转折角处形成沉积，最终形成砂堵。

（2）迂曲角度会显著影响迂曲裂缝中支撑剂的运移和砂堵现象的发生，在现场压裂施工的过程中应尽量避免大角度裂缝的形成。

（3）注入速率越大，支撑剂运移的越远。但是当裂缝转折角处形成支撑剂堆积时，增大注入速率只会更快更严重地形成砂堵。

（4）支撑剂的粒径并不是越小越好。较小的支撑剂形成支撑剂堆积比较致密，不容易使流体和支撑剂通过，会加重支撑剂封堵裂缝的程度。

（5）携砂液的密度对支撑剂的运移影响较小，但密度较大的携砂液会加快砂堵的形成，且加重支撑剂封堵裂缝的程度。

（6）支撑剂密度越大，在迂曲裂缝中形成砂堵的时间越慢。但是支撑剂密度并不是越大越好，较重的支撑剂会加重裂缝的封堵程度。

参考文献：

［1］ 张皎生，杨焕英，王晶，等.基于复杂缝网精细刻画的致密油气藏水平井多段压裂数值模拟技术［J］.中国海上油气，2023，35（4）：103-111.

ZHANG Jiaosheng， YANG Huanying， WANG Jing， et al. A method for numerical simulation of multi-stage fracturing of horizontal well in tight oil and gas reservoirs based on fine characterization of complex fracture network［J］.China Offshore Oil and Gas，2023，35（4）：103-111.

［2］ 敬季昀，兰夕堂，邹剑，等.裂缝型储层复杂人工裂缝压后定量诊断方法研究［J］.中国海上油气，2023，35（5）：185-192.

JING Jiyun， LAN Xitang， ZOU Jian， et al. Research of quantitative diagnosis of complex hydraulic fractures for fractured reservoirs［J］.China Offshore Oil and Gas，2023，35（5）：185-192.

［3］ 陈迟，郭建春，路千里，等.致密气藏多尺度支撑机理研究与应用［J］.西南石油大学学报（自然科学版），2022，44（3）：131-138.

CHEN Chi， GUO Jianchun， LU Qianli， et al. Research and application of multi-scale support mechanism in tight gas reservoir［J］. Journal of Southwest Petroleum University （Science & Technology Edition）， 2022，44（3）：131-138.

［4］ 高根英，张静娴，陈金峰，等.支撑裂缝导流能力的影响因素分析［J］.石化技术，2019，26（2）：91.

GAO Genying， ZHANG Jingxian， CHEN Jinfeng， et al. Analysis of factors influencing the inflow capacity of supporting fractures［J］. Petrochemical Technology， 2019，26（2）：91.

［5］ 王建明，邱钦宇，何讯超.搅拌罐内基于EDEM-FLUENT耦合的多相流混合数值模拟［J］.郑州大学学报（工学版），2018，39（5）：79-84.

WANG Jianming， QIU Qinyu， HE Xunchao. Numerical simulation of multiphase flow mixing based on EDEM-FLUENT coupling in a stirred tank［J］. Journal of Zhengzhou University （Engineering Edition）， 2018，39（5）：79-84.

［6］ 张超.基于CFD-DEM耦合的粗糙裂缝输砂机理及数值模拟研究［D］.青岛：中国石油大学（华东），2021.

ZHANG Chao. Research on sand transport mechanism and numerical simulation of rough fracture based on CFD-DEM coupling ［D］. Qingdao：China University of Petroleum （East China）， 2021.

［7］ 赵小薇.基于欧拉-拉格朗日方法的倒置液固流化床及喷动床流动特性数值模拟研究［D］.大庆：东北石油大学，2021.

ZHAO Xiaowei. Numerical simulation of flow characteristics of inverted liquid-solid fluidized bed and jet bed based on Euler-Lagrangian method［D］. Daqing：Northeastern Petroleum University， 2021.

［8］ LARRY H， HANNAH J， ROBERT R， et al. Dynamic experiments on proppant settling in cross-linked fracturing fluids［R］. SPE 8342， 1979.

［9］ NOLTE K G. Determination of proppant and fluid schedules from fracturing-pressure decline［J］. SPE Production Engineering， 1986，1（4）：255-265.

［10］ SIDDHAMSHETTY P， KWON J S. Modeling of hydraulic fracturing and designing of online pumping schedules to achieve uniform proppant concentration oil reservoirs［J］. Computer and Chemical Engineering， 2018，114（9）：306-317.

［11］ 戴天舒.基于DDPM的发动机复式油气分离器优化设计［D］.武汉：华中科技大学，2018.

DAI Tianshu. Optimized design of engine compound oil-gas separator based on DDPM［D］.Wuhan： Huazhong University of Science and Technology， 2018.

［12］ WELLER G， TABOR H. A tensorial approach to computational continuum mechanics using object-oriented techniques［J］. Computers in Physics，1998，12（6）：620-631.

［13］ ZENG Junsheng， LI Heng， ZHANG Dongxiao. Numerical simulation of proppant transport in hydraulic fracture with the upscaling CFD-DEM method［J］. Journal of Natural Gas Science and Engineering，2016，33：264-277.

［14］ HERTZ H. Ueber die beruehrung elastischer koerper［J］. Journal Für die Reine und Angewandte Mathematik， 1882，92：156-171.

［15］ MINDLIN R D， DERIESWICZ H. Elastic spheres in contact under varying oblique forces［J］. Journal of Applied Mechanics， 1953，20：327-344.

［16］ CHRISTOPH K， CHRISTOPH G， ALICE H， et al. Models， algorithms and validation for opensource DEM and CFD-DEM［J］. Progress in Computational Fluid Dynamics， 2012，12（2/3）：140-152.

［17］ ZHOUZ Y， KUANG S B， CHU K W， et al. Discrete particle simulation of particle-fluid flow： model formulations and their applicability［J］. Journal of Fluid Mechanics， 2010，661：482-510.

［18］ 任志安，郝点，谢红杰.几种湍流模型及其在FLUENT中的应用［J］.化工装备技术，2009，30（2）：38-40，44.

REN Zhian， HAO Dian， XIE Hongjie. Several turbulence models and their applications in FLUENT［J］. Chemical Equipment Technology， 2009，30（2）：38-40，44.

［19］ 王为术，徐维晖，翟肇江，等.PISO算法的实现及与SIMPLE， SIMPLER， SIMPLEC算法收敛性的比较［J］.华北水利水电学院学报， 2007，28（4）：33-36.

WANG Weishu， XU Weihui， ZHAI Zhaojiang， et al. Implementation of PISO algorithm and comparison of convergence with SIMPLE， SIMPLER and SIMPLEC algorithms［J］. Journal of North China Institute of Water Resources and Hydropower， 2007，28（4）：33-36.

［20］ LEONARD B P， MOKHTARI S. ULTRA-SHARP nonoscillatory convection schemes for high-speed steady multidimensional flow［R］. NASA Lewis Research Center 102568，1990.

［21］ HIRSCH C. Numerical computation of internal and external flows［J］. International Journal of Heat and Fluid Flow， 2007，10（4）：371.

［22］ TONG Songyang， MOHANTY K K. Proppant transport study in fractures with intersections［J］. Fuel， 2016，181：463-477.

［23］ HU Xiaodong， WU Kan， LI Gensheng， et al. Effect of proppant addition schedule on the proppant distribution in a straight fracture for slickwater treatment［J］. Journal of Petroleum Science and Engineering， 2018，167：110-119.

（编辑 李志芬）

基金项目：国家自然科学基金联合基金项目（U23B2084）

第一作者及通信作者：胡晓东（1990-），男，副研究员，博士，研究方向为水力压裂裂缝扩展/支撑剂运移机制、水力压裂诊断与评估、智能压裂。E-mail： huxiaodong@cup.edu.cn。

引用格式：胡晓东，张鹏天，周福建，等.迂曲裂缝内支撑剂运移数值模拟［J］.中国石油大学学报（自然科学版），2024，48（3）：111-118.

HU Xiaodong， ZHANG Pengtian， ZHOU Fujian， et al.