连杆曲线导引的织机开口机构设计

詹葵华 朱家程 白伦

DOI： 10.19398j.att.202310002

摘  要： 传统连杆开口机构难以使梭口保持停歇，无法适应高速、宽幅的现代新型织机的工艺要求。引入特殊连杆曲线导引的概念，利用带鲍尔点和带圆点连杆曲线能使从动件产生停歇的原理，设计了两种新型连杆开口机构。该机构由四连杆机构和综框导引组件组成，四连杆机构的曲柄、连杆、摇杆和机架杆杆长比分别为1∶2∶2∶2.76、1∶2∶2∶2.3，连杆点的位置角分别为62.49°、49.15°，其与摇杆相连的连接杆与连杆等长。综框运动规律显示：两种机构梭口满开时主轴的相对静止角分别为约150°，40°和200°；综框处于最高和最低位时速度和加速度均为0，表明综框运动平稳，无冲击。该机构突破了传统连杆开口机构的局限，为低成本新型织机的开发创造了条件。

关键词：织机；开口机构；四连杆机构；连杆曲线；梭口

中图分类号：TS103.1

文献标志码：A

文章编号：1009-265X（2024）06-0061-09

收稿日期：20230930

网络出版日期：20231216

作者简介：詹葵华（1968—），女，上海人，副教授，博士，主要从事机构学及纺织机械方面的研究。

织机开口机构旨在实现综框包含3个阶段的运动规律，即开启期、静止期和闭合期。为了使引纬过程顺利进行，综框停歇的“静止期”是多数织机开口工艺的一个重要条件［1-2］。由于凸轮机构的设计能更方便地实现从动件预期的运动规律，目前综框的开口运动往往由凸轮机构驱动［2-3］。除此之外，由电子系统和气动装置辅助的开口机构也常应用于新型织机中［4-5］。

以前的津田驹喷水织机和K611丝织机采用的是四连杆开口机构，而喷气织机则多采用六连杆开口机构［6］。由于综框升降缺少“静止期”，传统的连杆开口机构已无法适应现代织造对高速、宽幅的需求。多年来从连杆机构设计的角度解决匀速驱动条件下综框停歇问题的研究很少［7］，新近的研究提出通过变速驱动四连杆机构可使综框具有一定时间静止的新方法［8］。本研究引入特殊连杆曲线导引的概念，利用带鲍尔点和带圆点连杆曲线能使从动件产生停歇的原理，通过图解法和解析法设计了两种新型连杆开口机构。模拟结果显示，综框运动具有较长的停歇时间，符合织机开口的工艺要求。

1  带鲍尔点和带圆点的连杆曲线及其应用

连杆曲线通常是指平面四连杆机构中连杆平面上的点（即连杆点）的运动轨迹。由于连杆的运动复杂，连杆曲线呈现出的多样性一直受到机构学研究者的关注［9-10］。基于运动轨迹拟合和目标运动规律实现的方法被广泛应用于各类机械设备的设计中［11-13］。

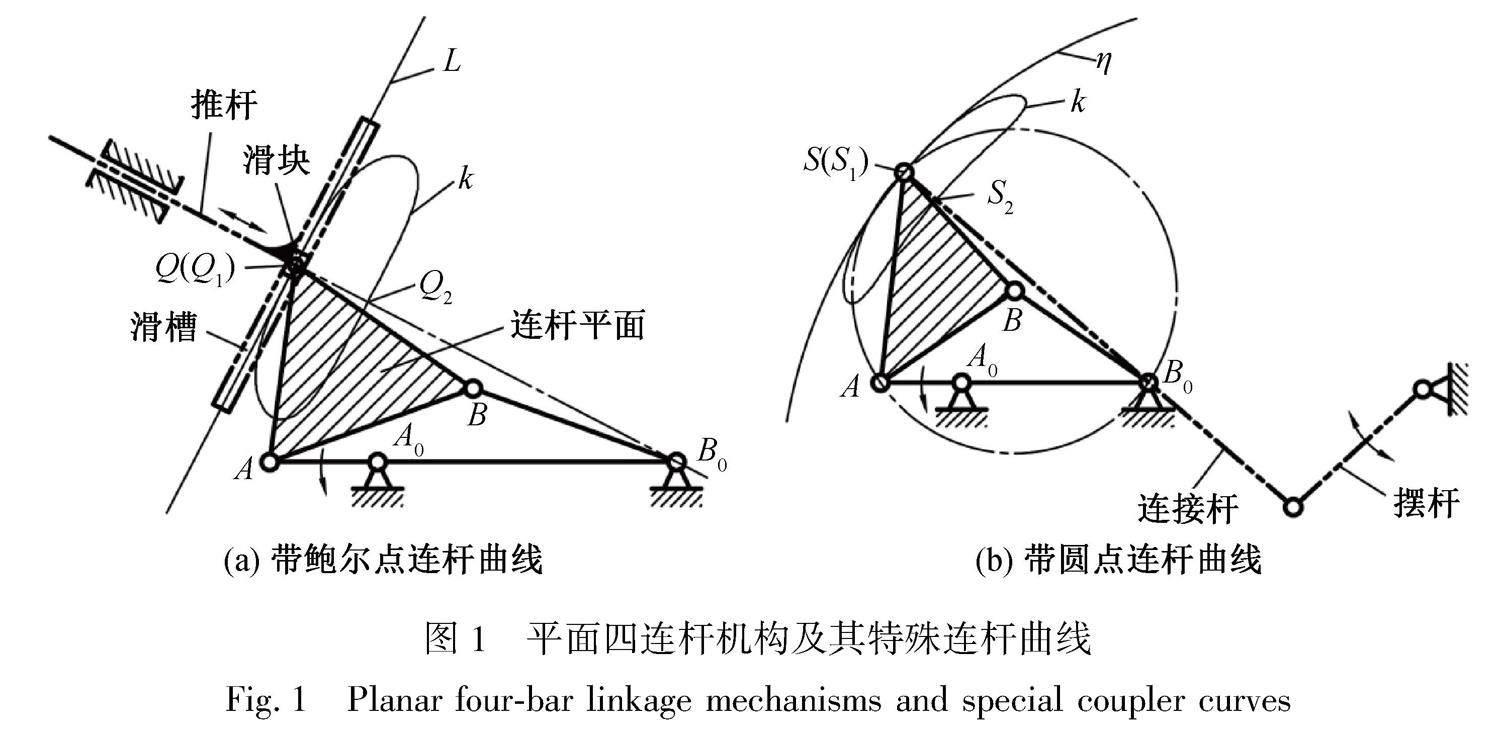
鲍尔点和圆点分别是指连杆曲线上与其切线和曲率圆三阶密切的位置点，带有鲍尔点和圆点的连杆曲线被认为具有较长的近似直线和近似圆弧，这一特性往往被应用于停歇机构的设计［14-15］。图1（a）—（b）分别显示了能生成带鲍尔点和带圆点连杆曲线的平面四连杆机构。其中，A0A为曲柄，AB为连杆，B0B为摇杆，A0B0为机架杆，Q和S为连杆平面上的连杆点。当机构杆长满足约束条件AB=B0B=BQ和AB=B0B=BS时［15］，Q和S的运动轨迹k即为对称连杆曲线。图1（a）中，Q的运动位置Q1为k上的鲍尔点。如将滑块与连杆点铰接，使其在T形推杆滑槽中移动，此时与切线L垂直的推杆在图示运动位置会出现短暂的停歇。图1（b）中，S1是连杆曲线k上的圆点。如将连杆点S串联连接杆和摆杆，当连接杆的杆长与曲率圆η半径相等时，摆杆在图示运动位置则会出现短暂的停歇。

2  双鲍尔点连杆曲线导引的开口机构I

2.1  对称双鲍尔点连杆曲线

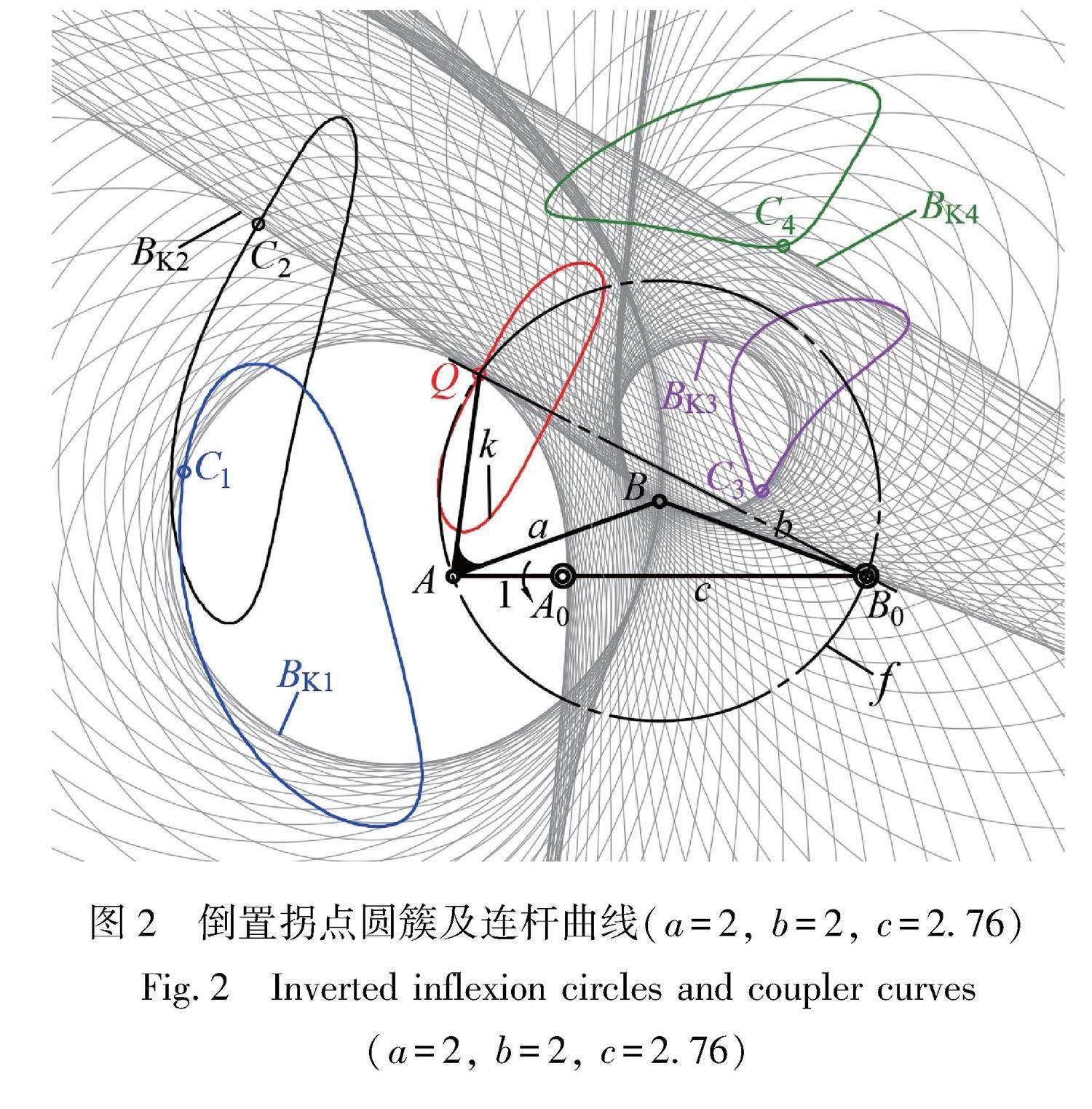
连杆曲线上的鲍尔点位于倒置拐点圆的包络线上［16］。如图2所示，设曲柄A0A=1，连杆AB=a=2，摇杆B0B=b=a=2，并取机架杆A0B0=c=2.76。将曲柄每隔2°对应的倒置拐点圆绘制成拐点圆簇（见图2中的细实圆），则可显示出包络线，如图2中的BK1、BK2、BK3和BK4。其上的连杆点C1、C2、C3和C4的运动轨迹带有一个鲍尔点，表现为有一段近似直线。BK1和BK2在圆f上的Q点处相切，表明Q点的运动轨迹同时具有两个鲍尔点。此时，Q点的位置角∠QAB=62.49°。如以图2曲柄的运动位置作为初始位置，即设曲柄转角φ=0°，由图1（a）所示的

（a=2， b=2， c=2.76）

该机构的机构简图可知，连杆点Q生成的运动轨迹k上的两个鲍尔点Q1（φ=0°）和Q2（φ=180°）同时位于其对称中心线B0Q上，即两段近似直线垂直于对称中心线。

2.2  双鲍尔点连杆曲线导引带停歇的综框运动

将图2的四连杆机构顺时针旋转62.49°，使k曲线的对称中心线B0Q处于竖直位置，然后串联综框的导引组件形成开口机构I，如图3所示：连杆点Q带动滑块在推综杆1的滑槽中移动，并带动推综杆1上下移动。在推综杆1的中间位置铰接连接杆1带动双臂摆杆摆动，并通过连接杆2带动推综杆2上下移动。推综杆1和推综杆2分别固联综框1和综框2，从而实现两层经纱的交替上升和下降。综框平面可根据具体情况设置为与机构所在平面垂直或者平行。

基于图2所示四连杆机构无量纲的尺度关系，使用SolidWorks 2021构建开口机构I的三维模型，尺寸单位取为0.1 m。算例模型示意图见图4（a），其中L1=100 mm，L2=200 mm，L3= 200 mm，L4=276 mm，L5=184.76 mm，L6=120 mm，L7=500 mm，L8=129.04 mm，D=60 mm，δ=62.49°。为使机构运动达到较好的可视化效果，设曲柄转速n=10 r/min进行运动仿真，综框1的运动规律见图4（b）。

图4（b）显示，由于连杆曲线上的鲍尔点与其切线呈三阶密切，综框在最高（φ=0°， 360°， …）和最低位置（φ=180°， 540°， …）时不仅存在明显的停顿，而且速度和加速度均为零，符合经纱在张力最大时避免抖动和冲击的工艺要求。

curve with two Ball's points

3  双圆点连杆曲线导引的开口机构II

3.1  对称双圆点连杆曲线

在连杆曲线上与其曲率圆三阶密切的圆点的集合称为圆点曲线ku，它通常是一条带二重点的三阶曲线。图5（a）—（b）分别显示四连杆机构两个特殊运动位置：内位置和外位置。当四杆机构处于这两个位置时，ku分解为圆ku′和直线ku′′，ku′的圆心O是AB0垂直平分线和通过B0B直线ku′′的交点［15，17］。相关符号在图5（a）和（b）中分别用下标1和2予以区别。基于生成对称连杆曲线的机构杆长约束条件，连杆点S的两个运动位置S1和S2分别位于圆点曲线ku1′（见图5（a））和ku2′（见图5（b））上，因此，此连杆曲线属于带有双圆点的对称曲线。

3.2  具有等曲率半径的双圆点对称连杆曲线

在图1（b）所示的机构中，如S1和S2均为圆点，为使摆杆在连杆点S运动到S1和S2时均实现短暂停歇，需确保圆点S1和S2处的密切圆曲率相等，且曲率半径为连接杆杆长。

如图5所示，已知P1和P2分别为内位置和外位置连杆的运动瞬心，设S10和S20分别为S1和S2处密切圆η1和η2的圆心，根据欧拉-萨伐里的动点轨迹曲率理论［17］，可得关系式：

1P1S1+1P1S10sin（α1）=1d1（1）

1P2S2+1P2S20sin（α2）=1d2（2）

式（1）—（2）中，P1S1的形式表示点P1和点S1间的距离（下同），d1和d2分别是连杆在两个运动位置的拐点圆（图中未标识）的直径，α1和α2分别是直线S1S10和S2S20与瞬心线切线T1和T2的夹角。依据博比利尔定理，机构处于内位置和外位置时，T1和T2分别与B0B1和B0B2所在直线重合［15］。

同理，针对连杆上的以A0为圆心转动的A点，有

1P1A1-1P1A0sin（β1）=1d1（3）

1P2A2-1P2A0sin（β2）=1d2（4）

式（3）—（4）中，β1和β2分别为A1A0和A2A0与瞬心线切线T1和T2的夹角。同样，设曲柄A0A=1，连杆AB=a，摇杆B0B=b=a，机架杆A0B0=c，根据几何关系有：

P1A1=1+c

P1A0=c

β1=arccosc+12a

P1S1=2acos（α1）

P1S10=R-P1S1

α1=90°-（δ+β1）（5）

以及

P2A2=c-1

P2A0=c

β2=arccosc-12a

P2S2=2acos（α2）

P2S20=R-P2S2

α2=（δ+β2）-90°（6）

式（5）—（6）中，δ为连杆点的位置角（见图5）；R为密切圆曲率半径，且有：

R=S1S10=S2S20（7）

将式（5）—（6）代入式（1）—（4），在四连杆机构杆长给定的情况下，合并方程，可得到一个包含未知量δ的方程，通过数值方法则可求得相应解。本研究解得的一组无量纲机构参数为：a=b=2，c=2.30，α1=6.44°，α2=30.18°，β1=34.41°，β2=71.03°，δ=49.15°，R=6.40，S1S2=0.52，其机构简图如图5所示。

3.3  双圆点连杆曲线导引带停歇的综框运动

将图5（a）所示的四连杆机构顺时针旋转49.15°，使连杆曲线的对称中心线B0S处于竖直位置，由连接杆、摆杆及综框推杆组成的综框导引组件与之串联，形成由双圆点连杆曲线导引的开口机构II，如图6所示：由镜像配置的两组连杆机构分别带动两页综框，相关标记用编号1和2予以区别。连接杆1和2的杆长为R；摆杆设置为上下摆动角度相等，综框推杆与摆杆的铰接位置可按综框输出动程的要求进行调节，本算例取摆杆长的0.85；曲柄1和曲柄2之间设有180°相位差，转向相反。图6显示开口机构II的两种配置方案，分别为综框推杆铰接位置与摆杆同侧的方案一（见图6（a））和异侧的方案二（见图6（b））。

为分析综框的运动规律，使用SolidWorks 2021进行算例的实体建模。基于四连杆机构无量纲的尺度数据，取尺寸单位为0.1 m。图7（a）为模型示意图，其中L1=100 mm，L2=200 mm，L3=200 mm，L4=230 mm，L5=261.63 mm，L6=639.77 mm，L7=200 mm，L8=900 mm，δ=49.15°。取曲柄转速n=10 r/min进行运动仿真，获得方案一中综框1的位移、速度及加速度随曲柄1的变化规律，如图7（b）所示。

由图7（b）可知，开口机构II中综框的运动规律与开口机构I（图4（b））相似，综框在最高和最低位置有明显的停顿，并且速度和加速度均为零，符合开口运动的工艺要求。

4  综框停歇及梭口对称度分析

4.1  综框停歇水平评估

梭口满开停顿是织机开口机构重要的设计指标。一般来说，有梭织机要求综框的静止角接近织机主轴的1/3转，即120°（对应曲柄旋转60°），而无梭织机对静止角要求较低。传统喷气织机使用的六

连杆开口机构，其静止角为0［6］。

本研究提出的开口机构I和II均能实现综框在极限位置保持一定时间的停歇。如以综框动程H0为基数，设综框位移为H（φ），综框高度的极限位置记为Hlim，用综框位移的相对误差ε来评估主轴相对静止角的大小，有：

ε/%=|H（φ）-Hlim|H0×100（8）

基于图4（b）和图7（b）的位移数据，对开口机构I和II中综框长停歇期和短停歇期对应的织机主轴相对静止角进行评估，结果见表1。

由表1可知，开口机构I在综框两个极限位置均存在较长的停歇，时间差异性小；而开口机构II对应的主轴两次相对静止存在较大的时间差异，适用于允许有上下层经纱满开停顿时间差要求的场合。在5%的相对误差范围内，开口机构I和II的静止角分别为约150°，40°和200°。

4.2  梭口上下对称度分析

将综框上、下动程的比值（≤1）作为梭口上下对称度指标，本研究提供的开口机构I和II的算例所对应的梭口对称度分别为0.83、0.52。

传统织机开口机构往往要求梭口具有上下对称性。连杆开口机构梭口的对称度可通过综框导引组件参数的选择进行调节。例如，针对开口机构I，本研究提供的算例是将双臂摆杆设定为综平水平，如将综平位置摆杆顺时针旋转30°，其综框1的上、下动程之比即可从0.83调整至0.98。

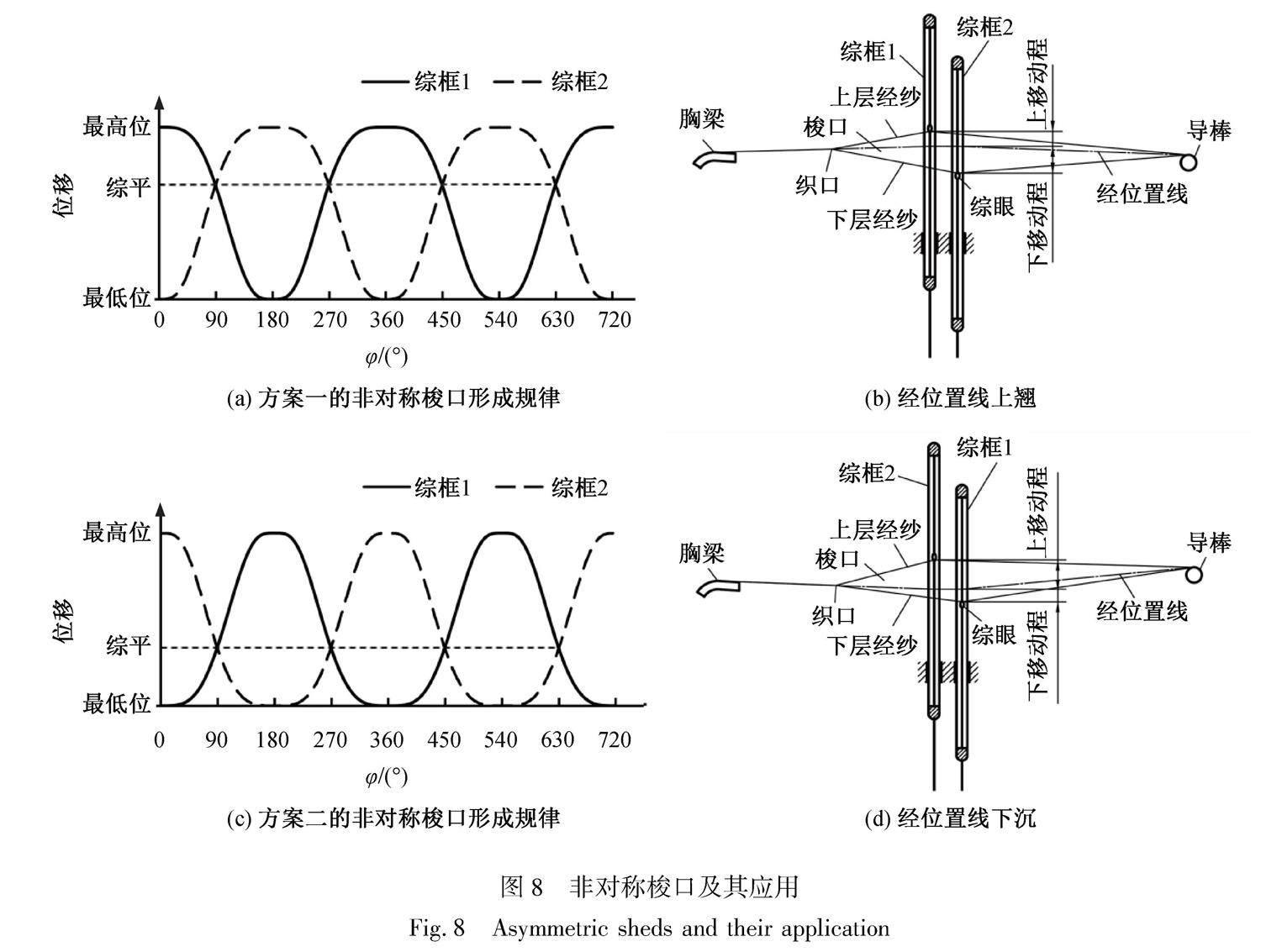
随着新型织机引纬方式的多样化，需要有开口、闭口角不同及不对称动程等多种形式梭口与之相适应［18-19］。动程非对称梭口已被应用于新型织机的设计中。理想的经位置线根据织物需求和引纬方式可选择上翘或下沉［20］。例如，当剑杆织机的经位置线为下沉状态时，综平时经纱除了上机张力，由于叠加了由附加伸长形成的张力，总张力变大，织物平整光洁。梭口满开时，上、下层经纱张力无差异，经纱断头少，开口清晰［18］。图8（a）显示开口机构II的方案一中两页综框的位移曲线，其特点为上层经纱动程小，下层经纱动程大，如应用于图8（b）所示的经位置线上翘的场合，可减小上层经纱的动态附加张力。图8（c）显示开口机构II的方案二中两页综框的位移曲线，其特点为上层经纱动程大，下层经纱动程小，如应用于图8（d）所示的经位置线下沉的场合，则可减小下层经纱的动态附加张力。

另外，增加下层经纱满开停顿时间、减少上层经纱停顿时间的非对称梭口的设计思想［21］与开口机构II的方案二（图8（c））相吻合。

4.3  与传统连杆开口机构比较

以前的四连杆和六连杆开口机构均不存在梭口满开的静止期。新近研究通过变速驱动实现了四连杆机构对综框三段式运动规律的控制［8］，而本研究的开口机构I通过匀速驱动即能实现综框三段式的运动规律，显示了开口机构I在设计方法上的有效性。不利用变速驱动，一种基于圆点连杆曲线导引的，能实现综框停歇的改进型六连杆机构［7］可作为本研究提出的开口机构II的对照机构进行比较。首先，开口机构II采用的是两组连杆机构，并通过两个单臂摆杆分别带动两页综框，使两页综框的运动规律清晰可控。对照机构是利用双臂摆杆带动两页综框，使其交替升降。由于综框上、下动程的对称度低，在主动综框的运动规律通过摆杆传递至从动综框过程中会出现难以避免的不清晰梭口或开口时间不稳定等问题，因此开口机构II更具应用性。其次，在连接杆杆长R（涉及开口设备的尺寸）与其竖直方向的动程S1S2（涉及输出的梭口大小）之比值方面，开口机构II为6.40/0.52，而对照机构为2.85/0.14［7］，对照机构约为开口机构II的1.7倍，说明开口机构II的结构更紧凑。

5  结论

带双鲍尔点连杆曲线和带双圆点连杆曲线均为特殊连杆曲线。利用鲍尔点处较长的近似直线和圆点处较长的近似圆弧可以引导综框实现梭口满开时停顿，为宽幅织机的顺利引纬提供保障。基于此原理，本研究提出了新型连杆开口机构I和开口机构II。两种机构均由四连杆机构和综框导引组件组成，四连杆机构的曲柄、连杆、摇杆和机架杆杆长比分别为1∶2∶2∶2.76、1∶2∶2∶2.3，连杆点位置角分别为62.49°、49.15°，其与摇杆相连的连接杆与连杆等长。模拟算例计算结果显示，当曲柄匀速转动，这两种机构综框的运动规律均符合开口运动的基本要求：a）梭口有明确的开启、静止和闭合的时间段，相对静止角分别为约150°，40°和200°；b）综框运动平稳，在两个极限位置时的速度及加速度均为0。

针对开口机构I和II，在所提供的模拟算例基础上，通过调整和优化机构参数，以及伺服电机的辅助，可以进一步开发适用于多种织造需求的开口机构。本研究显示了连杆曲线导引机构在纺织机械中的应用前景，使低副机构替代高副机构，为低成本织机的开发创造了条件。

参考文献：

［1］李盛铎. 连杆齿轮开口机构的分析和设计［J］. 纺织学报， 1993， 14（11）： 19-21.

LI Shengduo. Analysing and designing of link-gear shedding mechanism［J］. Journal of Textile Research， 1993， 14（11）： 19-21.

［2］季海彬，周香琴，成小军. 基于开口工艺要求的多臂机机构参数分析［J］．浙江理工大学学报（自然科学版）， 2016， 35（2）： 205-210.

JI Haibin， ZHOU Xiangqin， CHENG Xiaojun. Analysis on mechanism parameters of dobby based on requirement of opening process［J］. Journal of Zhejiang Sci-Tech University （Natural Sciences Edition）， 2016， 35（2）： 205-210.

［3］邱海飞，李春风，陈铭，等. 一种外置式高速织机共轭凸轮开口设计［J］. 机械设计， 2022， 39（11）： 1-6.

QIU Haifei， LI Chunfeng， CHEN Ming， et al. Design of high-speed loom's external conjugate cam shedding mechanism［J］. Journal of Machine Design， 2022， 39（11）： 1-6.

［4］陈登，梁海顺，马志燕. PLC控制液压电子开口装置的变频回路［J］. 现代纺织技术， 2005， 13（5）： 27-28.

CHEN Deng， LIANG Haishun， MA Zhiyan. Frequency-changing loop of PLC controlling hydraumatic electronic shedding motion［J］. Advanced Textile Technology， 2005， 13（5）： 27-28.

［5］ALA D M， ELIK N. Design of an electropneumatic shedding mechanism for a sampling loom［J］. The Journal of the Textile Institute， 2021，112（6）： 965-975.

［6］董慧琴，万根祥. 喷气织机六连杆开口机构分析［J］.纺织学报， 1982， 3（7）： 21-26.

DONG Huiqin， WAN Genxiang. The six-bar linkage shedding mechanism of air-jet looms［J］. Journal of Textile Research， 1982，3（7）： 21-26.

［7］杨玉萍，吴云，曹清林. 平面六连杆开口机构的改进设计［J］. 南通工学院学报（自然科学版），1996， 12（3）： 10-15.

YANG Yuping， WU Yun CAO Qinglin. An improved design for the planar six-bar linkage shedding mechanism［J］. Journal of Nantong Institute of Technology（Natural Science Edition）， 1996， 12（3）： 10-15.

［8］袁汝旺，魏晓. 变速驱动下电子开口机构运动学建模及工艺优化［J］. 天津工业大学学报， 2023， 42（1）： 81-88.

YUAN Ruwang， WEI Xiao. Modeling and craft optimization of electronic shedding mechanism under variable speed drive ［J］. Journal of Tiangong University， 2023， 42（1）： 81-88.

［9］HARTENBERG R S. Early coupler-point curves［J］. Journal of Mechanisms，1969， 4（2）： 167-170.

［10］刘文瑞，孙建伟，褚金奎. 基于小波特征参数的平面四杆机构轨迹综合方法［J］. 机械工程学报， 2019， 55（9）： 18-28.

LIU Wenrui， SUN Jianwei， CHU Jinkui. Synthesis method for path generation of a planar four-bar mechanism based on the wavelet feature parameters ［J］. Journal of Mechanical Engineering， 2019， 55（9）： 18-28.

［11］NOLLE H. Linkage coupler curve synthesis： A historical review： II. Developments after 1875［J］. Mechanism and Machine Theory， 1974， 9（3/4）： 325-348.

［12］CHANDRA SHEKHAR A， SHAIK H S， SHAHAB S. Analysis of Geneva mechanism using dwell symmetrical coupler curve mechanism［J］. Materials Today： Proceedings， 2021， 39：1402-1406.

［13］SHIWALKAR P B， Moghe S D， Modak J P， A novel approach to synthesis of double dwell crank rocker mechanisms［J］. International Journal of Mechanical and Production Engineering Research and Development， 2019， 9： 168-175.

［14］SANCHEZ-MARIN F， RODA-CASANOVA V. An approach for the global search for top-quality six-bar dwell linkages［J］. Mechanism and Machine Theory， 2022， 176： 104974.

［15］贝伊尔. 机构运动学综合： 平面机构尺寸综合理论基础［M］. 北京： 机械工业出版社， 1987： 84-243.

BEI Yier.Synthesis of Mechanism Kinematics： Theoretical Basis for Dimensional Synthesis of Planar Mechanisms［M］. Beijing： China Machine Press， 1987： 84-243.

［16］詹葵华，刘敬资. 连杆曲线直线导引有限接近法全面解［J］. 机械设计， 2009， 26（11）： 24-26.

ZHAN Kuihua， LIU Jingzi. Comprehensive solution on finite approaching method for straight line guidance of connecting rod curves［J］. Journal of Machine Design， 2009， 26（11）： 24-26.

［17］DIJKSMAN E E. Approximate straight-line mechanisms through four-bar linkages［J］. Romanian Journal of Technical Science： Applied Mechanics， 1972， 17（2）： 319-372.

［18］沈世德，吕仕元. 综框运动规律新探［J］. 纺织学报， 1991， 12（10）： 456-457.

SHEN Shide， L Shiyuan. An investigation on patterns of heald frame motion［J］. Journal of Textile Research， 1991， 12（10）： 456-457.

［19］GOKARNESHAN N， VARADARAJAN B， SENTHIL KUMAR C B. Mechanics of Shedding Motion in Weaving［M］//Mechanics and Calculations of Textile Machinery. Amsterdam： Elsevier， 2013： 135-144.

［20］王绍斌. 喷气织机的梭口形状尺寸对经纱张力变化的影响［J］. 四川纺织科技， 2002（4）： 10-12.

WANG Shaobin. Influence of air jet loom's shed dimension on warp tension［J］. Progress in Textile Science & Technology， 2002（4）： 10-12.

［21］陈明，毕丽蕴. 用于剑杆织机的一种非对称梭口的多臂［J］. 中国纺织大学学报， 1998， 24（1）： 66-67.

CHEN Ming， BI Liyun. About an asymmetrical shedding dobby for rapier looms［J］. Journal of China Textile University. 1998， 24（1）： 66-67.

Design of shedding mechanisms guided by coupler curves

ZHAN  Kuihua1a，  ZHU  Jiacheng2，  BAI  Lun1b

（1a.School of Mechanical and Electrical Engineering; 1b.College of Textile and Clothing Engineering，

Soochow University， Suzhou 215137， China; 2.School of Intelligent Manufacturing and Intelligent

Transportation， Suzhou City University， Suzhou 215104， China）

Abstract：

The loom shedding mechanism is designed to achieve the heald frame motion that includes three periods of opening， pause and closing. To ensure the easiest passage of weft carrier， the pause period is an important condition for most looms' shed-forming device. However， due to the lack of pause in heald frame motion， the traditional linkage shedding mechanisms have become difficult to adapt to the technological requirements for modern high-speed and wide-width looms， and cam shedding mechanisms are becoming more widely used.

This study introduces the concept of special coupler curve guidance and applies the principle that coupler curves with Ball's point or circling-point can make the follower pause to improve the previous design approaches of shedding mechanism. Specifically， because the coupler curves with Ball's point or circling-point have long approximate straight-lines or circular arcs， they can enable the heald frame as a follower to perform linear reciprocating movement with dwells at the limit positions by reasonable design.

In this paper， we proposed two novel linkage shedding mechanisms guided by the symmetric coupler curves with two Ball's points and two circling-points （hereafter called shedding mechanism I and shedding mechanism II）. The symmetric coupler curve with two Ball's points was obtained by a graphical method based on the inverted inflexion circles， while the symmetric coupler curve with two circling-points where the radii of curvature are equal

was obtained by the analytic method based on Euler-Savary's theory of curvature of point trajectory. In shedding mechanisms I and II， the length ratios of the crank， coupler， rocker and frame are 1∶2∶2∶2.76 and 1∶2∶2∶2.3， with the position-angles of the coupler-points of 62.49°and 49.15°， respectively， and the lengths of

the rods connected to the rockers are

equal to that of the couplers.

Additionally， in shedding mechanism I， the coupler-point directly drives the heald frame， while in shedding mechanism II， the heald frame is driven by a composite component composed of the connecting rod， swing-rod and pushing rod.

The results of the heald frame motion show that： （1） both shedding mechanism I and II can make the heald frames pause at two limit positions， with dwell times of around 150° as well as 40°and 200° （loom's main shaft angle）， respectively， indicating that there is a long shed dwell time; （2） the velocities and accelerations of the heald frames at two limit positions are both 0， indicating that the motions of the heald frames are stable， without flexible impact.

In conclusion， the proposed new linkage-type shedding mechanisms meet the requirements of loom shedding motion. Our study fully demonstrates application prospects of coupler curve guidance mechanisms in textile machinery， and the replacement of high pair with low pair will create conditions for the development of low-cost looms.

Keywords：

loom; shedding mechanism; four-bar linkage mechanism; coupler curve; shed