基于Bayesian-LightGBM模型的粮食产量预测研究
陈晓玲 张聪 黄晓宇
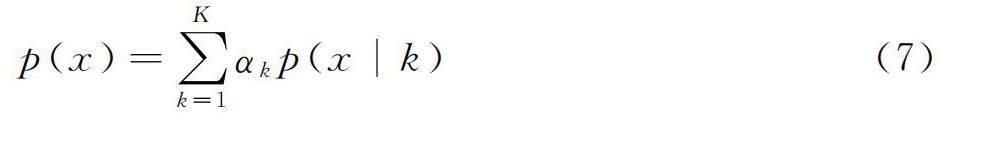

摘要:目前用于粮食产量预测模型如灰色关联模型普遍存在训练速度较慢、预测精度较低等问题。为解决该问题,以轻量级梯度提升机(LightGBM)模型为基础,将其损失函数修正为Huber损失函数,同时引入贝叶斯优化算法确定出最优超参数组合并输入该模型。以广西的早、晚水稻产量及16个粮食产量影响因素为数据集进行仿真试验,结果表明:基于线性回归的预测模型的平均绝对值误差为1.255,基于决策树的预测模型的平均绝对值误差为0.426,基于随机森林的预测模型的平均值误差为0.315,基于Bayesian-LightGBM的预测模型的平均绝对值误差为0.049。相比其他预测模型,Bayesian-LightGBM粮食产量预测模型能够更有效地实现粮食产量预测,预测精度更高。
关键词:粮食产量预测;粮食安全;轻量级梯度提升机;贝叶斯优化
中图分类号:S126; TP18
文献标识码:A
文章编号:2095-5553 (2024) 06-0163-07
收稿日期:2022年8月1日
修回日期:2022年9月29日
*基金项目:湖北省重大科技专项(2018ABA099);教育部科技发展中心重点项目(2018A01038)
第一作者:陈晓玲,女,1996年生,广东汕头人,硕士研究生;研究方向为人工智能技术及其应用。E-mail: cxl9612@163.com
通讯作者:张聪,男,1968年生,上海人,博士,教授;研究方向为基于农业和粮油食品领域的人工智能技术。E-mail: hb_wh_zc@163.com
Research on grain yield prediction based on Bayesian-LightGBM model
Chen Xiaoling1, Zhang Cong2, Huang Xiaoyu1
(1. School of Mathematics & Computer Science, Wuhan Polytechnic University, Wuhan, 430023, China;2. School of Electrical and Electronic Engineering, Wuhan Polytechnic University, Wuhan, 430023, China)
Abstract: At present, the grain yield prediction models, such as the grey relational model, generally have problems such as slow training speed and low prediction accuracy. In order to solve the above problems, this paper is based on the Lightweight Gradient Boosting Machine (LightGBM) model, and its loss function is modified to a Huber loss function, and a Bayesian optimization algorithm is introduced to determine the optimal hyperparameter combination and input into the model. Simulation experiments were carried out on the data sets of early and late rice yields and 16 grain yield influencing factors in Guangxi. The results showed that the average absolute error of the prediction model based on linear regression was 1.255, the average absolute error of the prediction model based on decision tree was 0.426, the average absolute error of the prediction model based on random forest was 0.315, and the average absolute error of the prediction model based on Bayesian LightGBM was 0.049. Compared with other prediction models, Bayesian LightGBM grain yield prediction model can realize grain yield prediction more effectively, with higher prediction accuracy.
Keywords: grain yield prediction; food security; Lightweight Gradient Boosting Machine; Bayesian optimization
0 引言
近年来,粮食安全问题已引起了世界各国的广泛关注,中国作为世界人口第一大国,确保粮食产量充足是国家发展的头等大事。为保证中国人口粮食供给充足,更好地规划粮食产量,科学有效预测粮食产量从而合理安排粮食的生产是解决粮食安全问题的关键手段[1-3]。
从现有文献来看,越来越多的学者开始围绕农业粮食产量问题展开探究。早期的粮食产量的预测模型效果不佳,如Donohue等[4]根据遥感农作物的吸收光合有效辐射、总太阳辐照度、漫射太阳辐照度和气温,建立C-Crop模型预测油菜和小麦的产量,但数据采集成本极高,且农作物识别精度不稳定,模型泛化能力差。韩书成等[5]利用线性模型和三点滑动平均发对粮食产量进行预测,但不足处是不能考虑其后要素突变对产量的影响,导致不能客观地反映气候变化对粮食产量的影响。孙东升等[6]运用HP滤波分析法将粮食产量数据分离为时间趋势序列和波动序列,并对趋势序列建立关于时间的趋势模型,提出由时间序列影响变动的因素构建的时间序列法,但时间序列法在建模过程中,不适合用在数据复杂的环境。Li等[7]提出一种灰色关联分析和BP神经网络结合的变量优化选择算法,采用灰色关联分析方法对输入变量的重要性排序,然后通过BPNN模型的多次训练和学习,得到关键变量和最佳BPNN模型结构,但缺点是模型结构复杂,存在大量的计算,模型训练速度慢。
为解决上述问题,本文采用LightGBM为基础模型,通过修正损失函数优化LightGBM模型,同时引入贝叶斯优化算法确定改进模型的超参数,以此建立Bayesian-LightGBM模型。以广西省早、晚水稻产量数据作为研究对象,将Bayesian-LightGBM模型应用于水稻产量预测中,并与机器学习领域常用的回归模型对比,验证Bayesian-LightGBM模型的有效性。
1 LightGBM模型
梯度提升决策树[8](Gradient Boosting Decision Tree,GBDT)是一种决策树[9]的算法,在各种领域的预测业务上发挥了重要的作用,但也存在训练时间过长、泛化能力弱等问题。针对这些问题,Ke等[10]对该算法做出了一系列的改进,并于2017年提出了一个支持高效率的并行训练GBDT算法框架——轻量级梯度提升机(LightGBM)。LightGBM因其高准确性、低内耗、运行速率快等优势被广泛应用于工业界。LightGBM模型通过使用直方图算法和带深度限制的按叶子分裂生长策略,提高了面对高纬度数据集的训练速度,解决了过拟合问题和预测精度低的问题。同时,LightGBM模型通过互斥特征捆绑算法,降低了特征维度,提高了了创建直方图的效率。
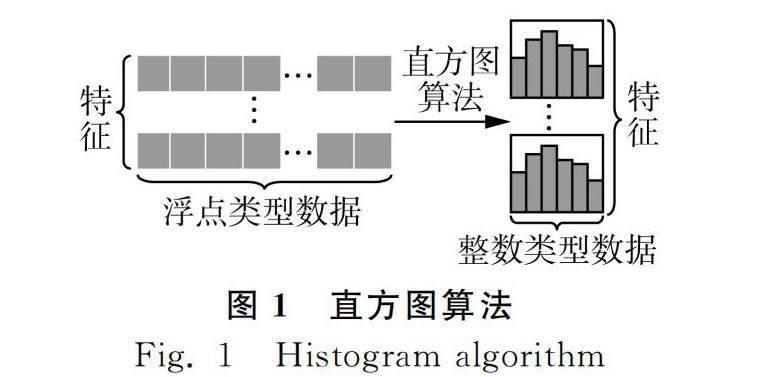
1.1 直方图算法
直方图算法将数据离散化,算法思路是把连续的浮点特征值离散化成K个整数,构造出一个宽带为K的直方图。直方图算法如图1所示。将遍历的数据根据离散化后的整数值作为索引在直方图中累计统计量,然后遍历直方图的离散值,找出决策树的最优的分割点。
特征值被离散化后,找出的分割点并不精确。由于决策树属于弱模型,分割点不精确并不影响最终模型训练的结果,但能减少大量的运算,降低内存的占用,提高训练的速度。
1.2 带深度限制的按叶子分裂生长策略
决策树的生长策略分为两类,一类是按层分裂生长策略;另一类是按叶子分裂生长策略。
1) 按层分裂的生长策略是分裂时将决策树中当前层的所有节点都进行分裂。该生长策略容易进行多线程优化,方便控制模型的复杂度,不容易过拟合,但有些分裂的节点增益很小,对这些节点分裂会导致该生长策略的效率不高。按层分裂生长策略如图2所示。
2) 按叶子分裂的生长策略是分裂时每次只选择增益最大的节点进行分裂。在分裂次数相同的情况,虽然按叶子分裂的生长策略比按层分裂的生长策略能降低更多的误差,获得更好的精度,但缺点是可能生长成深度较大的决策树,产生过拟合。因此LightGBM在选择按叶子分裂的生长策略时加上了最大深度的限制,通过最大深度来避免过拟合,按叶子分裂的生长策略如图3所示。
1.3 互斥特征捆绑
互斥特征捆绑(Exclusive Feature Bundling,EFB)算法目的是将数据集中互斥的特征捆绑一起,形成低维的特征集合,减少特征个数使数据规模进一步变小,有效地降低创建直方图的时间复杂度。通常为了不丢失信息,被捆绑特征都是互斥的,若两个特征不完全互斥,则用冲突比率衡量特征不互斥程度。当冲突比率较小时,可以把不完全互斥的两个特征捆绑,算法步骤具体如下:(1)将特征按非零值的个数进行排序;(2)计算不同特征之间得冲突比率;(3)遍历每个特征并尝试合并特征,使冲突比率最小化。
2 Bayesian-LightGBM模型
传统的LightGBM模型存在两点局限性,第一,真实场景下的粮食产量数据集含离群值,使用传统的回归模型损失函数会导致模型训练精度低等问题;第二,LightGBM模型在进行粮食产量预测时,需要确定最优超参数组合。不同的超参数对模型的性能有不同的影响。为增强模型对粮食产量预测的能力,具体改进如下。
2.1 修正损失函数
损失函数表示预测值与真实值的差距程度。传统的回归模型常用的损失函数有平均绝对值误差函数(MAE)、均方误差函数(MSE)。
1) 平均绝对值误差是指模型预测值f(x)与样本真实值y之间距离的平均值。
MAE=1m∑mi=1yi-f(xi)(1)
式中:m——样本数量;
yi——第i个样本真实值;
f(xi)——第i个样本预测值。
使用平均绝对值误差作为损失函数的优点是平均绝对误差对离群点不敏感,更有包容性,但是当梯度值较大时,该损失函数收敛性能较差且不利于模型的学习。
2) 均方误差是指预测值f(x)与样本真实值y直接距离平方的平均值。
MSE=1m∑mi=1[yi-f(xi)]2(2)
使用均方误差作为损失函数的优点是随着误差的减小,梯度也减小,有利于函数的收敛,但缺点是如果样本存在离群点,MSE会给离群点赋予更高的权重,这一方式牺牲了其他正常数据点的预测效果,导致模型整体性能降低。
3) Huber函数。针对数据存在离群点的问题[11, 12],上述传统回归模型常用的损失函数都存在一定的不足,因此,本文通过引入Huber损失函数,降低离群点的影响,增强模型的稳定性。Huber损失函数如式(3)所示。
Lδ(y,f(x))=12[y-f(x)]2y-f(x)≤δδy-f(x)-12δ2y-f(x)>δ(3)
式中:δ——Huber函数超参数。
δ值的大小决定了Huber损失函数侧重MAE还是MSE。当δ趋于0,Huber损失函数趋向于MAE;当δ趋于∞,Huber损失函数趋向于MSE。Huber损失函数同时具备了MSE和MAE的优点,降低了对离散值的敏感度,更有利于函数的收敛。
2.2 贝叶斯优化算法
在使用LightGBM模型进行训练的过程中需要确定出最优超参数组合。模型的超参数设定会直接影响模型性能。传统的自动调参方法有网格搜索、随机网格搜索与Halving网格搜索。网格优化超参数的本质都是在一个大参数空间中,尽量对所有点进行验证,再返回最优损失函数值,显然这种方法无法满足复杂模型的效率快和精度高的要求,且会耗费大量的计算资源和时间。贝叶斯优化算法[13]被认为是当前最为先进的优化框架,针对未知黑盒函数,贝叶斯优化[14]能够有效地利用历史信息,效率明显高于其他寻优方法。贝叶斯优化算法有两个很重要的组成部分,分别是概率代理模型和采集函数[15]。因此本文引入贝叶斯优化算法,对改进后的LightGBM模型参数寻优。
2.2.1 概率代理模型
概率代理模型包含先验概率模型和观测模型,其计算公式如式(4)所示。
p(f|D1:t)=p(D1:t|f)p(f)p(D1:t)(4)
式中:f——未知目标函数;
D1:t——已观测集合;
p(f)——先验概率模型;
p(D1:t|f)——观测模型。
当样本数据x为一维数据时,x服从高斯分布,其概率密度函数如式(5)所示。
p(x|θ)=12πσexp-(x-μ)22σ2(5)
式中:x——样本值;
μ——数据期望;
σ——数据标准差。
当样本数据x为多维数据时,x服从高斯分布,其概率密度函数如式(6)所示。
p(x|θ)=1(2π)D2|∑|12
exp-(x-μ)T∑-1(x-μ)2(6)
式中:D——数据维度;
∑——协方差。
高斯混合模型由k个单高斯模型构成,如式(7)所示。
p(x)=∑Kk=1αkp(x|k)(7)
式中:k——高斯模型的个数;
αk——第k个高斯模型的权重;
p(x|k)——第k个高斯模型的概率密度函数。
2.2.2 采集函数
采集函数则是根据后验概率分布p(f|D1:t)构造的,是确定下一个评估点的基准,本文选择置信度上界算法(Upper Confidence Bound,简称UCB)作为采集函数。具体如式(8)所示。
xt+1=argmax{μλ(x)+βσλ(x)}(8)
式中:μλ(x)——x的期望;
σλ(x)——x的标准差;
β——使在样本空间的开发和探索保持平衡[12]。
2.3 Bayesian-LightGBM模型训练过程
经优化损失函数的LightGBM模型,随机生成一组超参数,将训练集数据代入模型训练,使用贝叶斯优化算法调整模型的超参数。通过贝叶斯优化算法得到了最优超参数组合,将最优超参数输入模型得到Bayesian-LightGBM模型。具体过程如下:(1)随机生成一组超参数输入模型计算损失函数数值作为观测点;(2)通过观测点和混合高斯过程得到不同的置信区间;(3)用采集函数UCB计算概率密度估计,选取最大的置信度为新的超参数数值,将新超参数重新代入模型训练;(4)重复步骤2和步骤3,直到迭代次数达到预设值。选择模型预测准确率最高的超参数组合;(5)将最优超参数组合代入优化后的LightGBM模型,得到Bayesian-LightGBM模型。Bayesian-LightGBM模型流程如图4所示。
3 试验与分析
本研究采用的样本数据为2015—2018年广西壮族自治区的81县早、晚稻产量相关数据。本文运用平台为Intel(R) Core(TM) i7-6700HQ CPU,运用编程语言Python对数据进行处理、模型的构建和数据预测。试验过程中,采用线性回归、决策树、随机森林、XGboost、LightGBM作为对比模型,验证改进后的LightGBM模型的优越性。
3.1 试验数据
数据来源于广西壮族自治区大数据发展局提供的最新数据,由广西壮族自治区农业农村厅、广西壮族自治区气象局协助完成的数据特征采样。影响水稻耕作产量的因素众多,普遍认为生产措施、种子品种、灌溉施肥是影响水稻产量的因素,鲜有人研究气象对水稻产量的影响,因广西地块相对破碎,种植结构复杂,农业统计调查工作量大,通过预测天气和农作物生长的关系,为三农提供服务,对产业收割期意义重大。因此选取2015年1月—2018年12月总共132 951组检测的数据为原始样本,数据包含16个字段,其字段含义和数据类型具体如表1所示。
3.2 试验流程
原始数据划分为99 736个样本的训练集和33 215个样本的测试集。因原始数据存在数值差异较大和非数值型数据的情况,需经过预处理才能输入模型使用。对日照时数、日均风速、日降水量、日最高温度、日平均温度、日相对湿度和日平均气压用最大-最小标准化来归一化连续的特征处理,避免出现数据差较大的数据,使数据更平滑。区县id做独热编码处理。对4个时间段的风向特征数据做二维向量映射处理,由于风向一共有17种风向,如果对风向特征数据做独热编码处理会导致计算量太大,并弱化模型对其他特征的学习能力,因此按照每个风向对应的角度用正弦值和余弦值表示,4个时间段的风向特征经处理后统一为8个正余弦风向特征。年份、月份和日期三个特征的数据转用归一化的索引代表数据,将其合并成一个时间特征。为对比本文模型与其他机器学习模型在数据维度较高的情况下,能达到更好的预测效果,本文选取了数据集的16个特征作为原始数据集,经数据处理后为18个特征的数据。处理好的数据输入到Bayesian-LightGBM模型中,再通过贝叶斯优化算法对模型的超参数调优得出最优超参数组合,得到水稻产量预测最终模型。试验流程如图5所示。
3.3 评估指标
为验证粮食产量预测模型的有效性,选取平均绝对误差MAE、均方根误差RMSE、平均绝对百分比误差MAPE和决定系数R24个指标对模型评估,如式(9)~式(11)所示。
RMSE=1m∑mi=1(fi-yi)2(9)
MAPE=∑mi=1fi-yiyi×100m(10)
R2=1-∑mi=1(fi-yi)2∑mi=1(yi-yi)2(11)
式中:yi——水稻产量真实值;
yi——水稻产量真实值的平均值;
fi——模型输出水稻产量预测值。
3.4 模型性能对比分析
3.4.1 不同损失函数对比
在模型训练的过程,使用了不同的函数作为LightGBM的损失函数,试验结果如表2所示。
由表2可知,在迭代次数都是100次的情况下,MSE函数和Huber函数效果较好。在早水稻数据集下比较MAE指标,Huber函数比MSE函数要高0.9%,在RMSE指标中,Huber函数效果最好,为0.161。MAE函数作为LightGBM模型的损失函数,在水稻数据集的MAE指标和RMSE指标中都高达14以上,因MAE函数没有二阶导数,不合适作为LightGBM模型的损失函数。
3.4.2 不同超参数寻优方法对比
在模型训练的过程,使用了贝叶斯优化算法和网格搜索法进行对比,对模型的叶子节点数和树的最大深度进行优化。从表3可知,在优化方法迭代次数相同的情况下,早水稻数据集的MAE指标对比,贝叶斯优化方法为4.1%,网格搜索方法为5.6%。RMSE指标中,贝叶斯优化方法为6.1%,网格搜索为7.4%。综合来看,贝叶斯优化方法比传统的网格搜索方法在优化模型超参数上效果更好。
为验证本文提出的Bayesian-LightGBM模型的泛化能力和性能,将Bayesian-LightGBM模型与当前研究领域的经典的机器学习模型作对比试验。
对比图6与图7可知,图7中真实值与预测值的走势图比图6更接近,部分线是重合的,说明决策树模型预测的结果比线性模型预测的效果好,但真实值与预测值之间仍存在较大差距。
再将图7和图8对比观察,图8真实值与预测值的重合度比图7高,说明随机森林模型预测效果比决策树模型有所提高,但部分预测值与真实值存在差距,有待提高预测效果。将图9与图8对比,可以看到Bayesian-LightGBM模型预测点的真实值与预测值基本重合,说明Bayesian-LightGBM模型在预测时,预测点的真实值与预测值的差值比随机森林模型小。把图6~图9对比,可以看到在这4个图中水稻产量真实值与预测值重复度最高的是图9,说明Bayesian-LightGBM模型与另外3个对比试验模型的预测效果更好,预测值更接近真实值。
为更清楚地说明4个模型预测效果,根据试验评估指标,分别得到4个模型在早水稻数据集和晚水稻数据集的评估结果,具体如表4、表5所示。由表4可看出,在早水稻数据集的结果中,对比MAE值,Bayesian-LightGBM模型的MAE指标值最低为0.049,其次是随机森林模型0.315,最大值为线性回归模型,值为1.255。对于RMSE指标,Bayesian-LightGBM是4个模型中的最低值0.072。MAPE指标中,线性回归模型高达10.023,效果最好的模型是Bayesian-LightGBM,值为0.389。除了线性回归模型,其余3个模型在决定系数指标的值处于0.9~0.998之间,Bayesian-LightGBM模型高达0.998,其余模型均在0.96以下。根据表5的数据也可以得出与表4相似的结论。综合对比早晚水稻数据集的模型预测结果,Bayesian-LightGBM模型的预测性能最好,其次是随机森林模型,线性回归在4个模型中的预测能力最差。
3.5 水稻产量特征重要性分析
为了探究不同特征变量对模型的影响,以广西水稻数据作为数据集,使用18个特征变量作为特征集训练Bayesian-LightGBM水稻产量模型。由表6可知,水稻产量特征重要性的分布。在Bayesian-LightGBM模型利用特征训练过程中,区县id和日平均气压的重要度数值较高,说明这区县id特征和日平均气压特征对于水稻产量影响程度很大,其次是日平均风压特征和日最低温度特征。而日照时数特征和日均降水量特征的重要性相对较低,说明日照时数特征和日均降水量特征对于预测水稻产量的贡献较小。每个时间段的风向的特征重要性差距不大,说明各个风向对于水稻产量的影响程度相差不大。
4 结论
1) 针对粮食产量数据规模大、影响因子众多导致粮食产量预测模型训练速度慢、预测效果不佳,为了合理高效的规划粮食生产,本文以LightGBM模型为基础模型,采用Huber函数作为模型的损失函数,引进贝叶斯算法对模型进行优化,构建Bayesian-LightGBM粮食产量预测模型。
2) LightGBM模型存在超参数寻优问题,因此本文通过超参优化算法,改进LightGBM模型存在超参数的问题,具体作为是使用贝叶斯优化算法对LightGBM模型进行超参数寻优,得到最优超参数组合,试验结果表明,该方法提升模型的预测精度。
3) 结合实际数据验证,Bayesian-LightGBM模型预测效果良好,该模型的预测平均绝对误差为0.049,均方根误差为0.072,预测水稻产量结果与真实值比较接近,体现了其工程应用的价值。本文模型对比线性回归、决策树和随机森林模型,预测水稻产量的平均绝对误差分别降低1.206、0.377和0.266,证明Bayesian-LightGBM模型有效性,为粮食产量预测提供新的途径和方法。
参 考 文 献
[1]赵桂芝, 赵华洋, 李理, 等. 基于混沌-SVM-PSO的粮食产量预测方法研究[J]. 中国农机化学报, 2019, 40(1): 179-183.
Zhao Guizhi, Zhao Huayang, Li Li, et al. Study on method for food yield prediction based on chaotic Theory-SVM-PSO [J]. Journal of Chinese Agricultural Mechanization, 2019, 40(1): 179-183.
[2]胡程磊, 刘永华, 高菊玲. 基于IPSO-BP模型的粮食产量预测方法研究[J]. 中国农机化学报, 2021, 42(3): 136-141.
Hu Chenglei, Liu Yonghua, Gao Juling. Research on prediction method of grain yield based on IPSO-BP model [J]. Journal of Chinese Agricultural Mechanization, 2021, 42(3): 136-141
[3]施瑶, 陈昭. 基于SAFA优化LSSVM的粮食产量预测[J]. 中国农机化学报, 2019, 40(3): 144-148.
Shi Yao, Chen Zhao. Prediction of grain yield based on LSSVM optimized by SAFA [J]. Journal of Chinese Agricultural Mechanization, 2019, 40(3): 144-148.
[4]Donohue R J, Lawes R A, Mata G, et al. Towards a national, remote-sensing-based model for predicting field-scale crop yield [J]. Field Crops Research, 2018, 227: 79-90.
[5]韩书成, 李丹, 熊建华, 等. 广州市耕地资源数量变化及其对粮食安全的影响[J]. 农林经济管理学报, 2016, 15(6): 648-654.
Han Shucheng, Li Dan, Xiong Jianhua, et al. Changes in cultivated land amount and their impacts on food security in Guangzhou [J]. Journal of Agro-Forestry Economics and Management, 2016, 15(6): 648-654.
[6]孙东升, 梁仕莹. 我国粮食产量预测的时间序列模型与应用研究[J]. 农业技术经济, 2010(3): 97-106.
Sun Dongsheng, Liang Shiying. Research on time series model and application of grain yield prediction in my country [J]. Journal of Agrotechnical Economics, 2010(3): 97-106.
[7]Li Bingjun, Zhang Yifan, Zhang Shuhua, et al. Prediction of grain yield in Henan Province based on Grey BP Neural Network Model [J]. Discrete Dynamics in Nature and Society, 2021, 2021.
[8]Friedman J H. Greedy function approximation: A gradient boosting machine [J]. Annals of Statistics, 2001: 1189-1232.
[9]Quinlan J R. Induction of decision trees [J]. Machine Learning, 1986, 1: 81-106.
[10]Ke G, Meng Q, Finley T, et al. LightGBM: A highly efficient gradient boosting decision tree [J]. Advances in Neural Information Processing Systems, 2017, 30.
[11]Liang J, Gan Y, Song W, et al. Thermal-Electrochemical simulation of electrochemical characteristics and temperature difference for a battery module under two-stage fast charging [J]. Journal of Energy Storage, 2020, 29: 101307.
[12]Li X, Zhang L, Wang Z, et al. Remaining useful life prediction for lithium-ion batteries based on a hybrid model combining the long short-term memory and Elman neural networks [J]. Journal of Energy Storage, 2019, 21: 510-518.
[13]李亚茹, 张宇来, 王佳晨. 面向超参数估计的贝叶斯优化方法综述[J]. 计算机科学, 2022, 49(S1): 86-92.
Li Yaru, Zhang Yulai, Wang Jiachen. Survey on Bayesian optimization methods for hyper-parameter tuning [J]. Computer Science, 2022, 49(S1): 86-92.
[14]Mockus J B, Mockus L J. Bayesian approach to global optimization and application to multiobjective and constrained problems [J]. Journal of Optimization Theory and Applications, 1991, 70: 157-172.
[15]崔佳旭, 杨博. 贝叶斯优化方法和应用综述[J]. 软件学报, 2018, 29(10): 3068-3090.
Cui Jiaxu, Yang Bo. Survey on Bayesian optimization methodology and applications [J]. Journal of Software, 2018, 29(10): 3068-3090.

