钢轨轨底裂纹扩展影响因素分析

周宇 王蒙一 梁旭 姚凯洲

摘要： 【目的】为分析钢轨材质、残余应力、温度应力在钢轨使用中的内外因对轨底裂纹扩展的影响开展研究。【方法】基于断裂力学理论结合轨底伤损实测，建立钢轨轨底裂纹扩展模型，对轨底伤损扩展失效时的临界裂纹尺寸、裂纹平均扩展速率、剩余寿命等指标进行量化分析。【结果】结果表明：钢轨材料断裂韧性与轨底初始伤损扩展的剩余寿命存在正相关关系，U95Cr H材质钢轨的轨底裂纹扩展剩余寿命小于U78CrV H材质小于U75V H材质；以某线路实际使用的钢轨材质U78CrV H为例，轨底残余应力由0增加至300 MPa，轨底裂纹扩展的临界尺寸增长约2.5%，剩余寿命下降约6%；残余应力为200 MPa时，温度应力由0增加至200 MPa，轨底裂纹扩展的临界尺寸变化不大，在1%内。【结论】研究结果可为轨底裂纹扩展研究和养护维修提供参考。

关键词：钢轨；轨底裂纹；裂纹扩展；残余应力；温度应力

中图分类号：U213 文献标志码：A

文章编号：1005-0523（2024）02-0095-07

Analysis of Factors Affecting the Growth of Rail Bottom Cracks

Zhou Yu1，2， Wang Mengyi1，2， Liang Xu3， Yao Kaizhou1，2

（1. Key Laboratory of Road and Traffic Engineering of the Ministry of Education， Tongji University， Shanghai 201804， China；

2. Key Laboratory of Structural Durability and System Safety of Shanghai Rail Transit， Tongji University， Shanghai 201804， China；3. Metals & Chemistry Research Institute， China Academy of Railway Sciences Corporation Limited， Beijing 100081， China）

Abstract： 【Objective】In terms of the rail material， residual stress， temperature stress and other factors， work conditions are respectively designed to explore the influences of rail bottom crack expansion. 【Method】Based on the theory of fracture mechanics， combined with rail bottom measurement， the model of rail bottom crack expansion has been established and indicators such as critical crack size， average crack extension rate as well as remaining life has been quantified. 【Result】It is found that there exists positive correlation between the fracture toughness of rail material and the remaining life. The remaining life of U95Cr H is less than U78CrV H， which is less than U75V H. Taking U78CrV H， used in the line under test， as an example， when the residual stress grows from 0 to 300 MPa， the critical crack size grows by about 2.5% and the remaining life decreases by about 6%; and when the residual stress is 200 MPa， with the temperature stress from 0 to 200 MPa， the critical crack size does not change much and is within 1%. 【Conclusion】The research results of the article can provide reference for the research and maintenance of rail bottom crack propagation.

Key words： rail; rail bottom cracks; crack growth; residual stress; temperature stress

Citation format： ZHOU Y， WANG M Y， LIANG X， et al. Analysis of factors affecting the growth of rail bottom cracks[J]. Journal of East China Jiaotong University， 2024， 41（2）： 95-101.

【研究意义】钢轨伤损是影响铁路安全运行及维护的重大问题之一，特别是在轨底有初始伤损，车轮荷载通过时，轨底进一步受拉，给行车安全和钢轨使用状态带来严重威胁[1]。轨底伤损一般源于制造和铺设时的碰撞与运营中的腐蚀。其中，钢轨制造时产生的轨底伤损在出厂时能够被检验发现，风险可控。而在钢轨服役时由其所处环境引起的轨底锈蚀、轨底划痕等伤损，若探伤不及时，钢轨状态会因此迅速恶化，有断轨风险。

【研究进展】现有的无损检测技术[2-3]为钢轨轨底伤损及其次生裂纹的研究提供了基础，轨底锈蚀和划痕最初在钢轨横断面上呈半圆形。随着车轮反复作用在伤损区域上方的轨头处，该伤损在拉应力作用下沿轨底横向和垂向进一步扩展，且裂纹横向扩展速率逐渐大于垂向扩展速率，使得轨底伤损在钢轨横断面上逐渐演变为椭圆形，被称为“月牙伤”[4]。由于该处伤损的隐蔽性，被发现时多数已经在钢轨三维方向上演变成“椭球状”伤损[5]。

针对钢轨裂纹扩展的研究[6]，已有研究多采用有限元法[7]、统计概率法[8-9]等计算轨顶面已知位置处的表面滚动接触疲劳裂纹的尖端应力强度因子，进而预测其扩展行为。但鲜有研究针对轨底伤损展开深入研究。

轨底伤损在车轮荷载反复作用下，钢轨使用的内、外因素对由此形成的次生裂纹扩展影响非常重要。王建西等[10]指出在已有初始伤损的情况下，钢轨的断裂韧性体现了材料抵抗断裂扩展的能力。而在钢轨上道使用中，分布在其横断面的残余应力又加速或制约伤损开裂和发展[11]；由于轨温变化引起的无缝线路温度力又造成钢轨横断面的反复拉伸和压缩，是引起断轨的另一重要外因[12]。

【关键问题】上述对于钢轨材质、残余应力和温度应力主要是在轨顶面疲劳裂纹研究中，尚缺少其对轨底伤损和裂纹扩展的影响分析。【创新特色】本文基于三维椭球状轨底伤损的形态和显微特征，建立相应含曲面轨底初始伤损的有限元模型，考虑材质、残余应力、温度应力，基于断裂力学理论，结合有限元，量化分析裂纹扩展特征，为轨底裂纹扩展研究和养护维修提供参考。

1  建模过程

1.1  轨底伤损建模

含轨底伤损的钢轨取样自我国某铁路现场，为75 kg/m、U78CrV H轨。列车速度80 km/h，钢轨取样时累计通过总重约100 MGT（百万t）。沿垂直行车方向切取钢轨得到横断面，从轨底斜向上45 °对轨底伤损三维特征进行观测，如图1所示。

图1中红色虚线为轨底伤损轮廓线，黄色实线为椭圆拟合线，可以看出，轨底该伤损被发现时已近似呈椭球状。采用图像处理[6]对其尺寸进行识别，并沿其走向进行拟合，得到该伤损长3.93 mm，深1.50 mm，有沿轨头垂向及沿轨底横向扩展的趋势。

根据轨底该实测椭球状伤损在钢轨断面的走向和位置，建立轨底椭球裂纹空间形态分析模型，如图2所示。首先，建立长度为10 m的钢轨全局有限元模型，其中轨下轨枕和道床质量忽略不计，扣件、道床和基础弹性简化成集总弹簧[6]按扣件间距设置在轨底中部，钢轨全局模型的位移约束由车轮荷载按车辆转向架轴距施加在模型中得到。再截取上述全局模型中部位置长度为50 mm的钢轨作为分析轨底伤损及其次生裂纹的钢轨局部子模型，在这段钢轨的轨底中心处设置一定长度的长轴和短轴的椭球模拟伤损。

为避免上述轨底伤损的裂纹扩展计算时在裂纹尖端处（图2（d）中的黄色实线位置）产生的奇异性问题，采用断裂力学理论基于四分之一节点单元在裂纹尖端生成三圈“单元环”，最里层由奇异楔形单元组成的内环，其余两圈单元环是由六面体单元构成，包围在楔形单元的外围（图2（e））。为了反映裂纹面和裂纹尖端的奇异性，采用扩展有限元方法[8]，在裂纹尖端附近单元引入富集函数[9]

[μx = i∈NsNxμi + i∈NcutNxNxHxaj + i∈NtipNxα=14φαx bak] （1）

式中：[Nx]为单元形函数；[Ns]为常规节点集合；[Ncut]为贯穿单元的节点集合；[Ntip]为裂纹尖端周围单元的节点集合；[μi]，[aj]，[bak]分别为常规节点位移矢量、贯穿节点位移矢量、裂纹尖端节点位移矢量；[Hx]为反映裂纹体不连续性的跳跃函数；[φx]为反映裂尖奇异项及应力状态的附加函数。

1.2 计算方法

采用直接循环算法进行上述裂纹尖端扩展分析。以扩展有限元为基础，定义材料的断裂参数和疲劳参数，实现循环荷载下模型的裂纹扩展。

在循环次数满足方程和最大荷载下，断裂释放率满足断裂能释放率门槛值的条件下，裂纹的扩展基于修正的PARIS公式 [5] 为

[dadN = c3ΔGc4]              （2）

式中：[c3]， [c4]分别为裂纹扩展材料常数，可通过裂纹扩展实验拟合得到。

[KⅠ]，[KⅡ]，[KⅢ]分别为对应张开型裂纹（Ⅰ型裂纹）、滑开型裂纹（Ⅱ型裂纹）和撕开型裂纹（Ⅲ型裂纹）3种基本裂纹模式的应力强度因子[13]。采用M积分[14]计算尖端应力强度因子，作为裂纹起裂扩展的指标

[M = Γ1Wxini-Tkuk，ixi ds        i，k = 1，2]      （3）

[KⅠ = limr→0 σy2πr]             （4）

[KⅡ = limr→0 σxy2πr]           （5）

[KⅢ = limr→0 σyz2πr]           （6）

式中：[M]为裂纹尖端扩展的能量释放率；[Γ1]为任意一条裂纹尖端的积分路径；[W]为应变能密度因子；[Tk]为积分路径外法线方向主应力矢量；[r]为裂纹尖端任意点到微元的空间距离。本次模型中，当应力强度因子达到材料的断裂韧性[K1c]时，即认为不再处于稳态扩展范围。并将此时裂纹尖端弧长定义为临界裂纹尺寸。

1.3 影响因素确定

1.3.1 钢轨材质

钢轨材质属于影响钢轨裂纹萌生与扩展的内在因素，且不同钢轨种类如断裂韧性、弹性模量、泊松比、抗拉压强度等材质参数对裂纹寿命的影响也不相同，对裂纹萌生更为显著。本文选取U95Cr H、U75V H、U78CrV H （H为热处理）共3种钢轨，以探究不同材质的断裂韧性对钢轨轨底裂纹扩展的影响。

1.3.2 残余应力

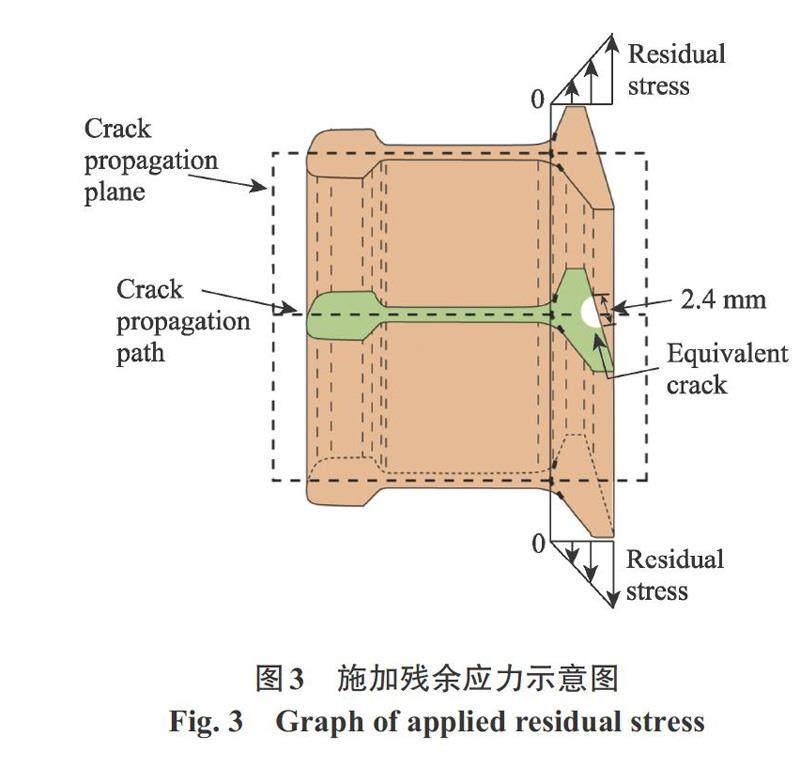
钢轨在制造和使用过程中均可能产生残余应力，而钢轨轨底残余应力会影响到运营安全。热轧过程中产生的冷却不均匀，矫直和调平，质量集中在轨头和轨底部分。此外，汪必升等[9]指出数值定义的残余应力比无残余应力模型更符合试验结果。压缩残余应力对材料的疲劳寿命、裂纹扩展和应力腐蚀具有有益影响。相比之下，拉伸残余应力会降低其性能。由于轨底处于受拉部位，其寿命大幅降低。参考王建西等[10]对新轨和旧轨的研究，设置0，100，200，300 MPa不同情况，将残余应力作为额外荷载[7]按照线性变化施加在钢轨轨底位置，如图3所示。

1.3.3 温度应力

由于钢轨接头阻力以及道床纵向阻力的抵抗，无缝线路中间及两端自由伸缩均受到限制。温度变化时，收缩受到限制而转化为温度力，作用于钢轨纵向。当存在轨底温度拉应力也可能造成断裂。因此在建模仿真过程中考虑温度拉应力。Xin等[11]指出钢轨截面温度应力变化不大并设置温度应力120 MPa，其对应于冬季条件下的温度变化[ΔTs]约50 ℃。Mirkovic等[12]同时指出在80 km/h及以下的行驶速度下，温度应力几乎可以不用考虑。综上，考虑到我国轨温差最不利地区，得到温度力171 MPa，对应于冬季条件下[ΔTs]约70 ℃。故在本次仿真模型中，全截面设置0，100，200 MPa温度应力进行分析，如图4所示。

2 模型验证

首先根据第1.1节的现场车辆轨道条件，建立车辆-轨道多体动力学模型，计算轮轨接触应力，将其作用于含有轨底伤损模型轨顶中心处，得到全局钢轨垂直位移，垂向最大位移出现在轮轨接触位置，为1.95 mm。此时，轨底椭球坑出现应力集中现象。再按1.1节所述方法在钢轨子模型底部插入圆心与轨底伤损曲面圆心相接的初始裂纹，按裂纹稳态扩展范围内进行扩展分析。

定义轨底裂纹扩展的应力强度因子（式（4）～式（6））达到材料的断裂韧性时为材料失稳，这时扩展的尺寸为裂纹临界尺寸；相应的裂纹向钢轨内部的扩展深度定义为裂纹深度；一定车轮通过次数下，裂纹深度的增量除以对应的车轮通过次数为裂纹扩展速率；达到裂纹临界尺寸时，裂纹各次扩展增量下的裂纹扩展速率平均值为裂纹平均扩展速率；裂纹从初始尺寸发展到临界尺寸的累计扩展次数为裂纹扩展的剩余寿命。

在试块切割过程中，假定裂纹按照扩展平面进行扩展，即认为通过钢轨底面椭圆心并沿列车运行方向切片，采用最细线切割，最大程度保护试块裂纹形态。再对切片以电子显微镜扫描。将模型所得裂纹扩展深度与多组现场真实情况进行比较，见表1。

钢轨服役期间，电镜观测到的最终裂纹实为多种因素共同作用下的结果，本文理论仿真条件为控制变量下的理想条件。根据现场实测结果，可以发现仿真结果包含于现场实测结果之中，处于观测结果中的上下限内，证实了所采用方法的合理性，可用于钢轨轨底裂纹扩展评估。

3 结果分析

3.1 钢轨材质对裂纹扩展的影响

金属材料抵抗断裂能力取决于断裂韧性。采用U75V H、U78CrV H、U95Cr H 3种不同断裂韧性的材质钢轨进行轨底裂纹扩展预测，均不考虑温度应力和残余应力作用。计算得到不同断裂韧性下轨底裂纹扩展到临界状态的尺寸与剩余寿命。其中，U75V H、U78CrV H和U95Cr H钢轨的断裂韧性[K1c]由实验得到，分别为36.0，35.7 MPa·m1/2和29.3 MPa·m1/2，并分别设置为相应钢轨材质下的轨底裂纹扩展至断裂失稳前的限值。

参考文献[5]，设定初始裂纹为一个半径是1.2 mm的半圆形，其方向与钢轨表面垂直，沿钢轨横断面向轨底内部扩展，可由式（1）～式（6）计算裂纹扩展。3种钢轨材质的轨底裂纹扩展到临界裂纹的尺寸、裂纹深度、面积、剩余寿命和裂纹的平均扩展速率，如表2所示。

计算结果表明，裂纹临界尺寸、裂纹深度、面积、裂纹平均扩展速率与钢轨的断裂韧性呈正相关，而剩余寿命与钢轨的断裂韧性呈负相关。这与许玉德等[15]的研究结果相一致，同时验证了模型的准确性。

从表2可知，当钢轨由U75V H依次更换为U78CrV H、U95Cr H时，材料断裂韧性[K1c]由36 MPa·m1/2下降为35.7 MPa·m1/2和29.3 MPa·m1/2，下降幅度分别约0.83%和18.61%，临界裂纹尺寸由63.5 mm分别增长到64.4 mm和65.0 mm，分别增长约1.4%和2.4%，说明随着材料断裂韧性的下降，裂纹更容易扩展增大；同理，裂纹剩余寿命由1.85×106次分别下降到1.84×106 次和1.77×106 次，分别降低约0.5%和4.3%，裂纹平均扩展速率由9.08×10-6 mm/cycle分别提高到9.29×10-6 mm/cycle和9.77×10-6 mm/cycle，分别加快约2.3%和7.6%。上述数据可以证实：当材料断裂韧性较小时，即阻止断裂失稳的能力较弱，相同荷载条件下表现在裂纹扩展更明显，扩展长度更大，深度更深。裂纹以更快速度扩展，即经历的循环次数更少，故剩余寿命更小。

3.2 残余应力对裂纹扩展的影响

以取样钢轨材质U78CrV H为对象进行残余应力对裂纹扩展影响的研究，基准工况无残余应力。分别设置轨底存在100，200，300 MPa的拉应力作对照，同时均不考虑温度应力影响。

不同残余应力作用下轨底裂纹扩展结果如表3所示，可以发现，其裂纹临界尺寸、裂纹深度、面积、裂纹平均扩展速率与残余应力呈正相关，而剩余寿命与残余应力呈负相关，与刘亮等[16]的研究相一致即裂纹平均扩展速率随着残余应力的增大而增大。

可以看出，当残余应力由0增加到100 MPa再200 MPa最终到达300 MPa时，裂纹临界尺寸由64.4 mm依次增加为64.7，65.7 mm和66.0 mm，最大增长约2.5%；剩余寿命由最初的1.84×106 次依次下降到1.80×106，1.78×106 次和1.73×106 次，最大下降约6%；裂纹平均扩展速率由最初的9.29×10-6 mm/cycle最终提高到1.01×10-5 mm/cycle，最大加快约9%。这是因为钢轨最初受力形式为上部受压下部受拉，残余拉应力作为额外荷载施加于钢轨下部，使得钢轨下部尤其是轨底部位的受拉程度进一步加剧。又由于轨底存在初始伤损，加速了裂纹的扩展，使得裂纹平均扩展速率增大，更快达到临界尺寸，即会在更短的循环次数后到达临界尺寸，故剩余寿命减小。

3.3 温度应力对裂纹扩展的影响

以取样钢轨U78CrV H为对象进行温度应力对裂纹扩展影响的研究，基准工况为无温度应力。分别设置100、200 MPa两组温度拉应力情况，同时，设置残余拉应力为200 MPa。

与残余应力作用结果相似，在已有200 MPa残余应力的基础上，随着温度应力不断增大，裂纹尖端向上（钢轨内部）扩展，使得裂纹临界尺寸、裂纹深度进一步增大。不同温度应力作用下，轨底裂纹扩展结果如表4所示，同样，裂纹临界尺寸、裂纹深度、面积、裂纹平均扩展速率与温度应力呈现正相关关系，而剩余寿命与温度应力呈现负相关关系。与文献[16]的研究结论一致。

从表4可知，当温度应力由0逐渐增加到100，200 MPa时，裂纹临界尺寸有增长，但增幅约在1%以内；剩余寿命由1.78×106 次下降到1.73×106，1.68×106 次，最大降低幅度约为5.6%，裂纹平均扩展速率由9.78×10-6 mm/cycle提高到1.00×10-5，1.05×10-5 mm/cycle，最大加快约7%。临界裂纹尺寸在残余应力恒定200 MPa时，温度应力的变化对其造成的影响不大。这是由于模型在全断面施加温度应力，原本钢轨横断面的受力状态上压下拉，轨头部分中和一部分温度应力，轨底部分承受来自温度应力和残余应力两部分表现为拉力的额外荷载，加速了钢轨轨底受拉特性，同时也加速了裂纹的扩展，使得裂纹平均扩展速率提高，更快达到临界尺寸，故剩余寿命进一步下降。

4 结论

1） 钢轨材质改变，使得材料断裂韧性下降时（从U75V H到U95Cr H），材料断裂韧性下降约18.61%，轨底裂纹扩展的剩余寿命会下降约4.3%，呈正相关。裂纹达到临界失效时的尺寸会因断裂韧性降低而增长约2.4%，扩展速率提升约7.6%，呈负相关。

2） 轨底残余拉应力由0增加至300 MPa，轨底裂纹达到临界失效时的尺寸增长约2.5%，剩余寿命下降约6%，扩展速率加快约9%。

3） 钢轨残余应力为200 MPa时，其温度应力由0增加至200 MPa，轨底裂纹达到临界失效时的尺寸变化不大，在1%内，剩余寿命下降约5.6%，扩展速率加快约7%。

参考文献：

[1]    吕晶， 杨其全， 许鑫， 等. 重载铁路直线段钢轨断裂原因分析[J]. 铁道建筑， 2021， 61（11）： 124-127.

LYU J， YANG Q Q， XU X， et al. Cause analysis of rail fracture in straight section of heavy haul railway[J]. Railway Engineering， 2021， 61（11）： 124-127.

[2]    REN G P， SUN Z R， DAI X Y， et al. Laser ultrasonic nondestructive evaluation of sub-millimeter-level crack growth in the rail foot weld[J]. Applied Optics， 2022， 61（22）： 6414-6419.

[3]    LI Y， LIU Z， ZHENG Y F， et al. Transverse crack detection of rail base considering wedge-like structure and using a bulk-wave electromagnetic acoustic transducer[J]. IEEE Transactions on Instrument and Measurement， 2022（71）： 1-9.

[4]    RODRIGUEZ S， GAYOUX V， DUCASSE E， et al. Ultrasonic imaging of buried defects in rails[J]. NDT & E International， 2022（133）： 102737.

[5]    ROMANO S， BERETTA S， GALLI G S， et al. Determination of inspection intervals for welded rail joints on a regional network[J]. Procedia Structural Integrity， 2017（4）： 87-94.

[6]    李骏鹏， 周宇， 梁旭， 等. 钢轨轨顶弯钩形滚动接触疲劳裂纹空间扩展特性研究[J]. 铁道学报， 2022， 44（7）： 125-134.

LI J P， ZHOU Y， LIANG X， et al. Research on propagation characteristics in 3D space of hook-type rolling contact fatigue crack in top of rail[J]. Journal of the China Railway Society， 2022， 44（7）： 125-134.

[7]    IORIO A D， GRASSO M， KOTSIKOS G， et al. Development of predictive models for fatigue crack growth in rails[J]. Key Engineering Materials， 2012 （188/189）：13-16.

[8]    ROMANO S， MANENTI D， BERETTA S， et al.  Semi-probabilistic method for residual lifetime of aluminothermic welded rails with foot cracks[J]. Theoretical and Applied Fracture Mechanics， 2016（85）： 398-411.

[9]    汪必升， 李毅波， 廖雅诗， 等. 基于扩展有限元模型的动态应力强度因子计算[J]. 中国机械工程， 2019， 30（11）：1294-1301.

WANG B S， LI Y B， LIAO S Y， et al. Calculation of dynamic stress intensity factors based on XFEM model[J]. China Mechanical Engineering， 2019， 30（11）： 1294-1301.

[10]  王建西， 许玉德， 肖伟. 钢轨材质参数对疲劳裂纹萌生寿命影响的敏感性分析[J]. 石家庄铁道学院学报（自然科学版）， 2009， 22（1）： 15-19.

WANG J X， XU Y D，XIAO W. Sensitivity analysis of material parameters of rail to fatigue crack initiation life[J]. Journal of Shijiazhuang Tiedao University （Natural Science Edition） 2009， 22（1）： 15-19.

[11]  XIN H，VELJKOVIC M. Residual stress effects on fatigue crack growth rate of mild steel S355 exposed to air and seawater environments[J]. Materials & Design， 2020， 193：108732.

[12]  MIRKOVIC N， POPOVIC Z， PUSTOVGAR A， et al. Management of stresses in the rails on railway bridges[J]. FME Transactions， 2018， 46（4）： 636-643.

[13]  李庆芬. 工程断裂力学[M]. 哈尔滨： 哈尔滨工程大学出版社， 2005.

LI Q F. Engineering fracture mechanics[M]. Harbin： Harbin Engineering University Press， 2005.

[14]  BUDIANSKY B， RICE J R. Conservation laws and energy-release rates[J]. Journal of Applied Mechanics， 1973，40（1）：201-203.

[15]  许玉德， 徐国尧， 李凤煜， 等. 腐蚀钢轨剩余疲劳寿命研究[J]. 兰州交通大学学报， 2020， 39（4）： 1-9.

XU Y D， XU G Y， LI F Y， et al. Study on residual fatigue life of corroded rail[J]. Journal of Lanzhou Jiaotong University， 2020， 39（4）： 1-9.

[16]  刘亮， 王文健， 郭俊， 等. 高速铁路钢轨剩余疲劳寿命预测研究[J]. 机械强度， 2012， 34（4）： 590-596.

LIU L， WANG W J， GUO J， et al. Prediction of residual fatigue life for high-speed railway rail[J]. Journal of Mechanical Strength， 2012， 34（4）： 590-596.

通信作者：周宇（1977—），男，副教授，博士，博士生导师，研究方向为钢轨伤损，轨道结构。E-mail：yzhou2785@tongji.edu.cn。