单元审视·四基引领·范式建构

【关键词】高中数学；单元审视；四基引领；范式建构；幂函数

【中图分类号】G633.6  【文献标志码】C  【文章编号】1005-6009（2024）19-0047-02

【作者简介】曾荣，江苏省教育科学研究院（南京，210013）高中数学教研员，正高级教师，江苏省数学特级教师。

高中数学教学倡导“突出数学主线，凸显数学的内在逻辑和思想方法”“整体把握教学内容，促进数学学科核心素养连续性和阶段性发展”“既要重视教，更要重视学，促进学生学会学习”［1］2，82。2023年10月11—13日，杨玲玲老师在江苏省高中青年数学教师优秀课观摩与评比活动中执教的“幂函数”一课，获得了一等奖。这节课在单元审视中研读教材提炼主线，在四基引领中帮助学生提升素养，在范式建构中促进学生学会学习，值得教师认真学习和借鉴。

一、单元审视，主线清晰，前后贯通

深刻理解教材是上好一节课的基础。研究教材不能仅将视角聚焦在本节课所教的某一节内容，而要善于用单元的视角去研读教材。所谓单元的视角，就是用一种联系的观点、整体的视角去看问题。教师在研读教材时，既要善于将研究的视角前移，去思考新知的关联情境、知识基础、方法基础等，又要善于将研究的视角后延，去思考知识运用、结论推广、方法迁移等。

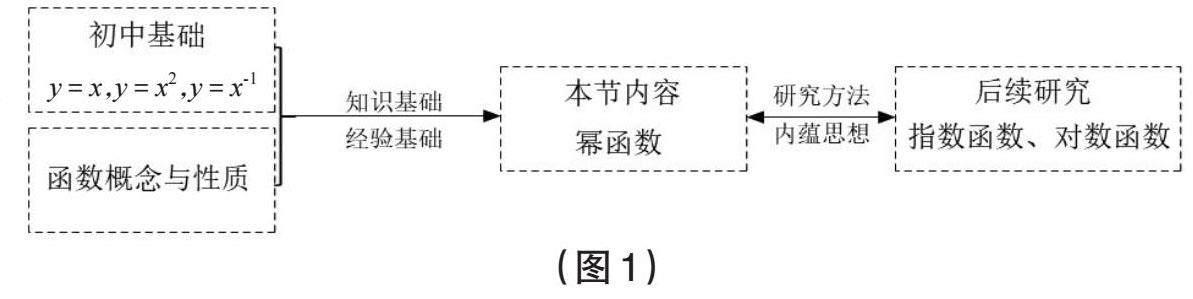
从前后知识关联的视角看，本节所学的幂函数与初中所学的y = x，y = x2，y = x-1以及高中已学的函数概念与性质密切相关，后者是前者的知识基础，并为幂函数的学习提供了基本的学习经验。同时，幂函数的研究方法、内蕴的数学思想与后续的指数函数、对数函数等基本上是一致的。从这个意义上说，用单元的视角研读教材，就形成了如下的逻辑主线。（见图1）

从具体实施来看，本节课直接依托6个特殊函数结构上的一致性，通过抽象概括生成幂函数的定义，接下来从数与形两个角度，引导学生通过动手作图、GGB演示、理性思考等方式去研究这些函数的图象和性质。在深刻领悟幂函数图象与性质的基础上，数学应用就水到渠成了。基于以上认识，关注知识生成的逻辑性，就形成了如下的教学主线。（见图2）

二、四基引领，培养能力，提升素养

《普通高中数学课程标准（2017年版2020年修订）》指出：“四基”是培养学生数学学科核心素养的沃土，是发展学生数学学科核心素养的有效载体。教学中要引导学生理解基础知识，掌握基本技能，感悟数学基本思想，积累数学基本活动经验，促进学生数学学科核心素养的不断提升。［1］81

杨玲玲老师在执教过程中，善于利用最近发展区原则，依托学生已有的知识基础、经验基础去设置问题。例如，借助问题“在以往的学习中，我们学习过函数的哪些基本内容？”引导学生回顾已学知识，引出本节课研究的几个特殊函数，并搭建了研究的基本框架，使得后续研究自然而有序。又如，借助问题“函数y = x2的奇偶性可以如何得到？”引出研究函数问题的两种常用视角：依图识性和依性作图，为后续的研究带来方法的指引。再如，借助问题“你能根据已有的学习经验来研究y = x3，y = x[12]，y = x-2的图象和性质吗？说说你的设想。”启发学生借鉴以往的学习经验设计合理的研究方案。并在此基础上，让学生运用数形结合的思想，深入探究幂函数的图象与性质。经历对以上问题的深入研究，后续师生们在研究问题“根据第一象限特征，结合奇偶性，幂函数的图象共有多少类？”这类对思维要求较高的问题时，借助数形结合思想就迎刃而解了。

三、范式建构，注重思维，强化方法

为了形成科学有效的研究方案，教师要善于运用头脑风暴集思广益，让学生对问题进行全面系统的分析或将问题进行分解，使其更具体、更清晰，进而抓住主要矛盾，找到问题的关键点，确定问题的研究方向。长期进行这样注重方法形成的教学，有利于学生形成科学探究的自觉，达到“授人以鱼，不如授之以渔”的目的。［2］

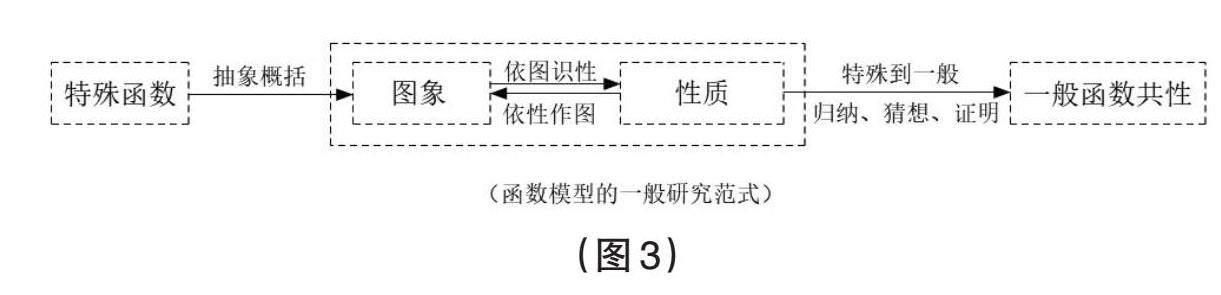
杨玲玲老师在“总结升华，形成系统”环节，提出问题“本节课主要研究了哪些内容？是如何研究的？研究一个新函数的途径和策略是什么？我们还能研究什么？”通过这样的问题帮助学生进行反思升华。事实上，幂函数作为一个特殊的函数模型，这只是一个例子，通过这个示例的学习，可以帮助学生形成如下图的研究函数的一般范式（见图3）。而这个研究范式的形成则是内蕴于幂函数学习的全过程之中的。

“数学在形成人的理性思维、科学精神和促进个人智力发展的过程中发挥着不可替代的作用。”［1］1教师要努力“将理性思维的培养融入数学教学，让新知生成有理有据，让思想方法根植课堂”［3］。

【参考文献】

［1］中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［S］.北京：人民教育出版社，2020．

［2］曾荣.学即研究——以研究性学习引领学生数学素养的形成［J］.江苏教育，2016（23）：16-18．

［3］钟志华.将理性思维的培养融入数学教学［J］.江苏教育，2023（37）：24-25．