贫数据条件下燃料电池汽车故障分类方法

聂振宇 李良雨 张广秀 陈帅 张晓辉

【欢迎引用】 聂振宇，李良雨， 张广秀， 等. 贫数据条件下燃料电池汽车故障分类方法[J]. 汽车文摘，2024（XX）： 1-11.

【Cite this paper】 NIE Z Y， LI L Y， ZHANG G X， et al. Fault Classification Methods for Fuel Cell Vehicles under Poor Data Conditions [J]. Automotive Digest （Chinese）， 2024（XX）：1-11.

【摘要】燃料电池汽车是未来汽车工业可持续发展的重要方向，但现存燃料电池整车相关的测试评价标准尚未对燃料电池汽车存在的故障类型及其分类进行深入研究，缺乏统一故障分级分类方案。为改善该问题，提出一套完善的燃料电池汽车故障模式的分级分类评价指标以统一相关故障等级，重点研究在缺乏数据条件下的燃料电池汽车故障分类方法。基于因子分析法和模糊集理论，提出一种针对燃料电池汽车在贫数据条件下的故障模式分类评价方法，为燃料电池汽车故障等级的分类提供指导意见。

关键词：燃料电池汽车；贫数据；故障分类；模糊集理論；因子分析法

中图分类号：U469.72   文献标识码：A  DOI： 10.19822/j.cnki.1671-6329.20230260

Fault Classification Methods for Fuel Cell Vehicles under Poor Data Conditions

Nie Zhenyu1，2， Li Liangyu1，2， Zhang Guangxiu1， Chen Shuai1，2， Zhang Xiaohui1，2

（1.China Automotive Technology & Research Center Co.， Ltd.， Tianjin， 300300; 2. CATARC Automotive Test Center （Tianjin） Co.， Ltd.， Tianjin， 300300）

【Abstract】 Fuel cell vehicle （FCV） is an important direction for the sustainable development of the automotive industry in the future. However， existing test and evaluation standards for FCVs have not thoroughly examined the types of faults and their classification. There is a lack of a unified fault grading classification scheme. To solve this issue， a comprehensive set of grading classification evaluation indicators for FCV faults is proposed to standardize the levels of related faults. The focus is on researching methods for classifying FCV faults in the case of lack of data. Based on factor analysis and fuzzy set theory， a fault mode classification evaluation method for FCVs under data scarcity conditions is proposed， offering guidance for the classification of FCV fault levels.

Key words： Fuel cell vehicle（FCV）; Data deficiency; Fault classification; Fuzzy set theory; Factor analysis method

0 引言

相比于传统汽车，燃料电池汽车具有零排放、高效率、低噪声的优势，受到日本、欧洲、美国等国家的广泛关注[1-2]。随着燃料电池汽车关键技术不断突破并在部分车型上应用，氢燃料电池汽车产业化不断加速[3]。我国燃料电池汽车多采用电-电混合技术路线，在续驶里程及整车成本方面具有明显优势，但耐久性、可靠性等性能指标与国外部分发达国家差距较大。虽然燃料电池系统的关键零部件已实现国产化，但到目前尚未有量产车型投放市场。对燃料电池汽车的故障类型及其所属类别不明确，成为限制其发展的主要因素之一。

我国已对燃料电池汽车发展进行了布局规划，制修订了多项燃料电池整车相关的测试评价标准，在GB/T 39132—2020《燃料电池电动汽车定型试验规程》[4]提出可靠性行驶试验过程中不应出现1、2类故障。然而，目前尚未对燃料电池汽车存在的故障类型及其分类进行研究，各整车制造商对于故障分级分类混乱，需提出一套完善的燃料电池汽车故障模式的分级分类评价指标以统一相关故障等级。

本文提出了一套针对燃料电池汽车故障分类的评价指标体系，该体系从故障性质、故障概率、故障后果和环境影响等维度进行构建。在数据相对贫乏的条件下，采用模糊集理论和专家评判的方法实现了对故障可能性和后果的定量分析。为确定各评价指标的权重，采用因子分析法旨在减弱主观性评价。根据多维评价指标的计算结果，实现了对燃料电池汽车故障的分类和分级。本文为燃料电池汽车的安全性研究提供了新的视角，为燃料电池汽车故障分类体系的建立提供了一种新的思路和方法，实现了在数据贫乏条件下进行故障定量分析，对推进燃料电池汽车的安全性研究具有一定的指导意义。

1 研究背景

1.1 燃料电池汽车

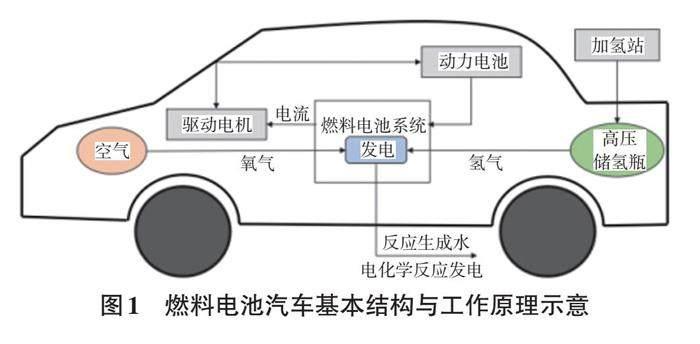
燃料电池汽车具有清洁、能效高的优点，在汽车市场的渗透率逐步提高。燃料电池汽车主要使用氢气或甲醇为主要燃料，通过电堆將化学能转化为电能，以驱动车辆。尽管其结构简单，但燃料电池汽车需要大功率、高动态响应的燃料电池系统，且长时间频繁的变载工况会使燃料电池寿命衰减。为了克服以上问题，燃料电池和动力电池的电-电混合技术方案成为目前国内燃料电池研究重点。该技术方案的典型结构见图1[5]。

1.2 故障分类

从安全性和故障的严重程度出发，可以将燃料电池汽车故障分为4级。1级故障：对燃料电池汽车造成安全性的损伤，如影响氢、电安全和启动运行，一旦发生必须紧急切断开关进行安全保护。2级故障：这类故障会影响车辆的正常工作及性能。若不及时处理，该故障会存在恶化风险。3级故障：这类故障仅会轻微影响系统，但不会造成致命性的危害。4级故障：这类故障不影响整体功能，可以忽略不计。

2 基础理论分析

2.1 综合评价模型

对本文研究的燃料电池故障分类，建立对应指标评价体系。对各项指标的相对重要性进行量化，从多个评价指标对其进行评价，以减少主观性判断，尽可能提高准确性。对每一项指标单独进行评分，并根据指标对应权重，对所得指标评分进行修正，将各个修正后的指标评分进行求和。最终，得到某一燃料电池汽车故障的综合评价水平，确定其所属分类。

[Yi=i=1pAij×Wij（i=1，2，…，m）]              （1）

式中：Yi为燃料电池汽车故障综合评价水平，p为故障的评价指标个数，m为评价水平所分析的故障数，i为故障个数，Aij为第i个故障的第j个指标的标准化值，Wij为第i个故障的第j个指标在所有指标中所占的权重。

2.2 因子分析法

本文采用因子分析法计算指标的权重。因子分析是一种统计学方法，用于分析复杂数据集中的变量之间的相互关系和结构。其通过对数据进行降维，提取变量之间的关系，进而得到一些解释性更强、与原始数据相关性更好的因子用于理解数据。因子分析通常需要输入1个包含2个或者2个以上变量的数据集，然后通过选定主成分个数和因子旋转方式等参数获得预期结果。

因子分析的基本思想是通过对变量进行压缩，提取可以解释变量之间关系的构建成分（即因子），并将这些因子用于数据的降维和解释。通过因子分析，可以将众多的观测变量归纳为更少的一些潜在因子，这些因子之间存在一定程度的相关性，并且可以反映出原始数据集中的一些重要信息和结构性关系。因子分析有助于理解数据、简化数据处理流程、提高预测准确率等。

3 燃料电池汽车故障评价指标体系

3.1 指标体系构建原则

考虑构建燃料电池汽车故障评价指标体系的合理性和正确性，主要遵循以下原则：

（1）科学性：在构建过程中要从官方渠道获得数据，更真实的量化分析。

（2）全面性：由多个指标构成，需大量阅读参考文献，全面准备构建评价指标体系所需要的辅助资料。

（3）可量化原则：选择指标要考虑能否可量化，以便进行计算和分析，以确保定量分析结果具有可比性。

3.2 指标内容及其计算方法

构建燃料电池汽车故障的评价指标，可以从故障性质、故障概率、故障后果（对人员生命或财产造成损害或后果的严重性）、环境影响等方面进行。由于数字对比相对更直观清晰，因此需要对各个指标进行量化分析。

根据故障表现特征对故障性质进行等级划分，故障表现特征包括：检测性故障（1）、警示性故障（2）、功能性故障（3）[6]，3种表现特征的严重程度依次递进为了便于后续分析计算，将语言转化为数值，分别用数值1、2、3表述。考虑到目前燃料电池汽车数量较少，缺少对应的故障数据样本，因此采用模糊集理论（Fuzzy Set Theory，FST）计算燃料电池汽车故障概率与后果[7-8]。通过专家对事件的主观语言判断，将定性分析转换成定量的数值分析[9]。并对专家给出的数值进行权重平均，得到综合多位专家意见的模糊概率评分。

通过测量氢气泄露浓度评估其对环境影响，将故障导致的泄露或尾气排出的氢气浓度划分为4个等级[10]，见表1。

4 燃料电池汽车故障综合评价

4.1 数据收集与整理

考虑到燃料电池汽车涉及多个系统，潜在故障数量庞大，本文仅选取燃料电池系统作为研究对象，并总结了常见的故障模式，见表2。在上述理论研究和评价指标体系构建的基础上，运用专业统计服务科学平台（Scientific Platform Serving for Statistics Professional，SPSSPRO）软件对数据进行处理。

将各燃料电池故障发生的可能性分为非常低、低、中等、高和非常高5个等级。利用梯形模糊数，将模糊语言转换成数值语言[11]。语言变量对应梯形模糊数见表3。

通过增加专家人数可以缩小专家意见偏差，使结果更接近真实值。考虑到研究可操作性，邀请了3位业内专家进行评价[12]，采用FST分别对燃料电池汽车各发生故障的可能性和严重度进行分析，将模糊语言转化为能够代表多个专家的综合评估分数。以发生故障的可能性为例，得到发生故障可能性的聚合后模糊数，见表4。

故障发生将对人员、财产和环境造成不同程度的影响。专家综合考虑各方面因素，对故障造成的后果进行评估，并采用模糊集理论，构建了故障严重度的聚合模糊数，见表5。

收集到的原始数据进行二次整理计算，对于梯形模糊数M={u，m1，m2，l}可利用模糊重心法去模糊化，具体原理为：

[X*=u（x）xdxu（x）dx， 其中u（x）xdx≠0]               （2）

式中：X*为输出值，[u（x）]为隶属度函数，x输出变量。

对式（2）进行推导，可得其重心公式：

[CN=（u2+m22+um2-l2-m21-lm1）3（m2+u-m1-l）]         （3）

式中：[CN]即为去模糊化后的结果。

最终，得到各项故障的发生可能性以及对应故障后果的综合评分，见表6。

4.2 数据处理与分析

首先对燃料电池故障分类的原始数据进行抽样适合性检验（Kaiser-Meyer-Olkin，KMO）和巴特利特（Bartlett）球形度检验，判断是否可以进行因子分析，见表7。

由表7可得，KMO的检验值为0.718，适合做因子分析。对于Bartlett的检验，显著性远小于0.01，说明各变量间具有相关性，因子分析有效。

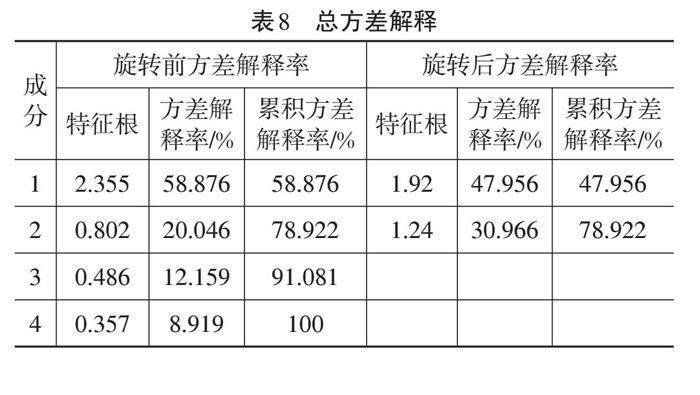
对主成分和累计方差贡献率进行计算，通常情况下进行主成分分析，主成分1和主成分2的累计方差贡献率在80%左右，选取的主成分需能反映大部分原有指标。表8为样本数据的总方差解释情况。

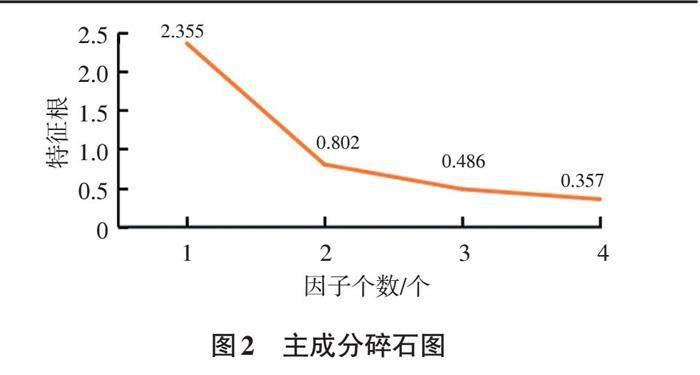
根据各主成分对数据变异的解释程度绘制成碎石图（图2），利用特征值下降的坡度确认所需选择的因子主成分个数，选取前2个公因子。

计算因子载荷矩阵和成分得分系数矩阵。因子载荷矩阵中的某列数值除以对应主成分特征值得到各指标的成分得分系数。燃料电池汽车故障分类旋转后的因子载荷系数和成分矩阵见表9。

将原始数据与成分得分系数矩阵相乘，得到各主成分的得分结果，主成分得分F的计算表达式为：

F1=0.063*A1-0.384*A2+0.321*A3+0.302*A4                 （4）

F2=1.19*A1-0.049*A2+0.528*A3+0.479*A4                   （5）

F=（0.48/0.789）*F1+（0.31/0.789）* F2                                （6）

式中：F为主成分得分，F1为成分1的得分，F2为成分2的得分，A1为故障性质，A2为故障可能性，A3为后果评估，A4为环境影响。

根据主成分得分计算综合得分，对其进行降序排序，得到各燃料电池故障类型的综合得分与排名情况，见表10。

将故障划分为4个等级，综合得分＞1分为1级故障，综合得分0～1分为2级故障，综合得分－1～0分为3级故障，综合得分＜－1分为4级故障[13]。最终，对燃料电池汽车系统的故障等级進行分类及综合评分结果见图3。

5 结束语

本文分析了燃料电池汽车在贫数据条件下的故障分类，构建了燃料电池汽车故障评价指标内容及其计算方法，为整车厂提供一种燃料电池汽车故障等级的分类方法。对各项指标进行数据收集，采用因子分析法对数据进行处理，根据得分区间，将各个故障分为4个故障等级，对燃料电池汽车系统的故障等级进行故障等级分类。

通过综合因子分析和模糊集理论，本研究提出了一种针对贫数据条件下燃料电池汽车故障分类的新方法，实现了故障等级的有效评价。此方法结合数据和专家判断，弥补了传统计算方法可能忽略重大故障概率的不足，为燃料电池汽车系统故障的精准分类提供了一种可行途径。

参 考 文 献

[1] ZHAO F Q， MU Z X， HAO H， et al. Hydrogen Fuel Cell Vehicle Development in China： An Industry Chain Perspective[J]. Energy Technology， 2020， 8（11）： 2000179.

[2] HAUER K H. Analysis Tool for Fuel Cell Vehicle Hardware and Software （Controls） with an Application to Fuel Economy Comparisons of Alternative System Designs[J/OL]. Institute of Transportation Studies， Working Paper Series， 2001[2024-04-15]. https：//ideas.repec.org/p/cdl/itsdav/qt52g0c0

3n.html.

[3] WIPKE B K， SPRIK S， KURTZ J， et al. Fuel Cell Vehicle and Infrastructure Learning Demonstration Status and Results[J]. ECS Transactions， 2019， 16（2）： 173-184.

[4] 国家市场监督管理总局， 中国国家标准化管理委员会. GB/T 39132—2020： 燃料电池电动汽车定型试验规程[S/OL]. （2020-10-11）[2024-05-01]. https：//openstd.samr.gov.cn/bzgk/gb/newGbInfo？hcno=667FED7F07C1C55433F1767

4C1F7120C.

[5] 马睿， 党翰斌， 张钰奇， 等. 质子交换膜燃料电池系统故障机理分析及诊断方法研究综述[J].中国电机工程学报， 2024， 44（1）： 407-427.

[6] 周苏， 胡哲， 文泽军. 基于K均值和支持向量机的燃料电池在线自适应故障诊断[J]. 同济大学学报（自然科学版）， 2019， 47（2）： 255-260.

[7] SAATY T L， VARGASL G. Models， Methods， Concepts and Applications of the Analytic Hierarchy Process[M]. New York： Springer Science and Business Media， 2001.

[8] 李新宏， 朱玉娇， 李成成， 等. 贫数据条件下海底电缆故障概率评估方法[J]. 中国安全生产科学技术， 2022， 18（6）： 224-229.

[9] 康劲松， 康婷. 基于FTA-AHP的FCEV动力系统可靠性影响因子及其权重研究[J].电源学报， 2013（4）： 1-7+25.

[10] MIRI LAVASANI S M， YANG Z， FINLAY J， et al. Fuzzy risk assessment of oil and gas offshore wells[J]. Process Safety and Environmental Protection， 2011， 89（5）： 277-294.

[11] FERDOUS R， KHAN FAISAL， SADIQ REHAN， et al. Handling and Updating Uncertain Information in Bow-Tie Analysis[J]. Journal of Loss Prevention in the Process Industries， 2011， 25（1）： 8-19.

[12] 刘斌. 燃料电池系统故障诊断识别策略发展[J]. 船电技术， 2023， 43（4）： 1-4.

（责任编辑 明慧）