从课本的一道习题谈起

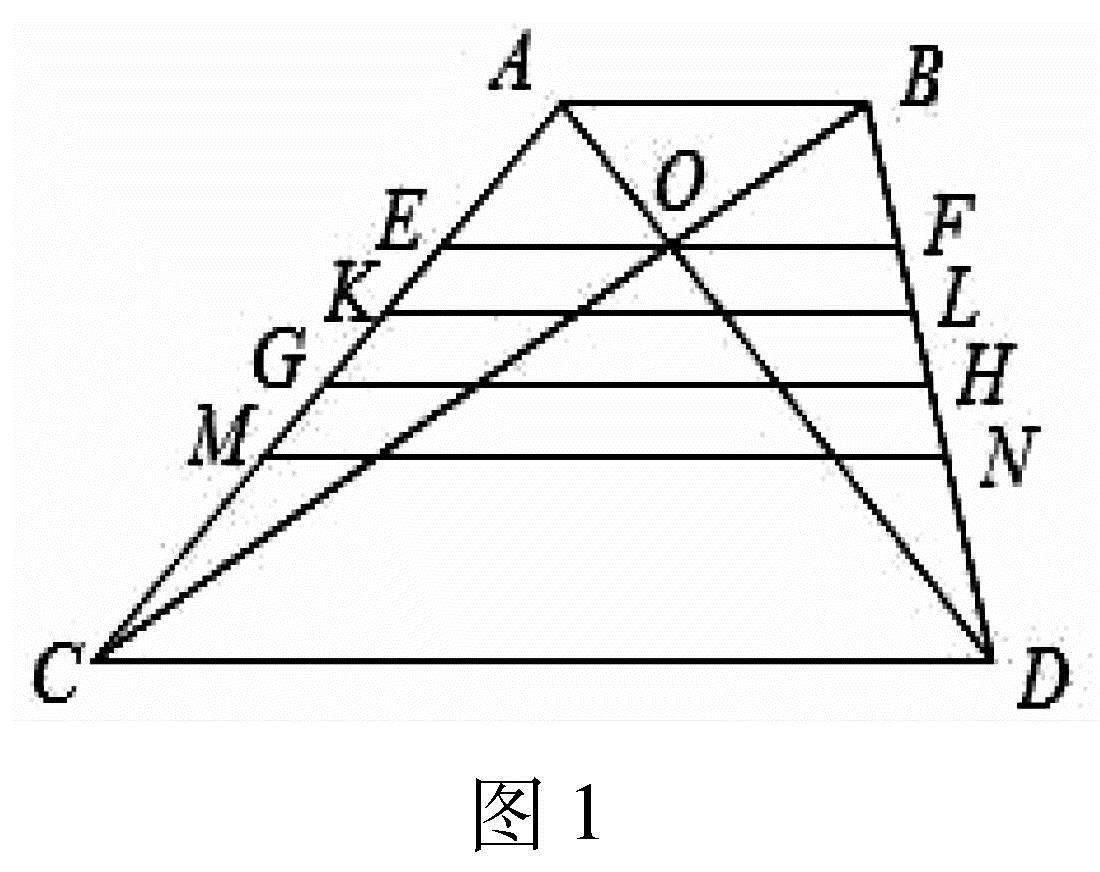
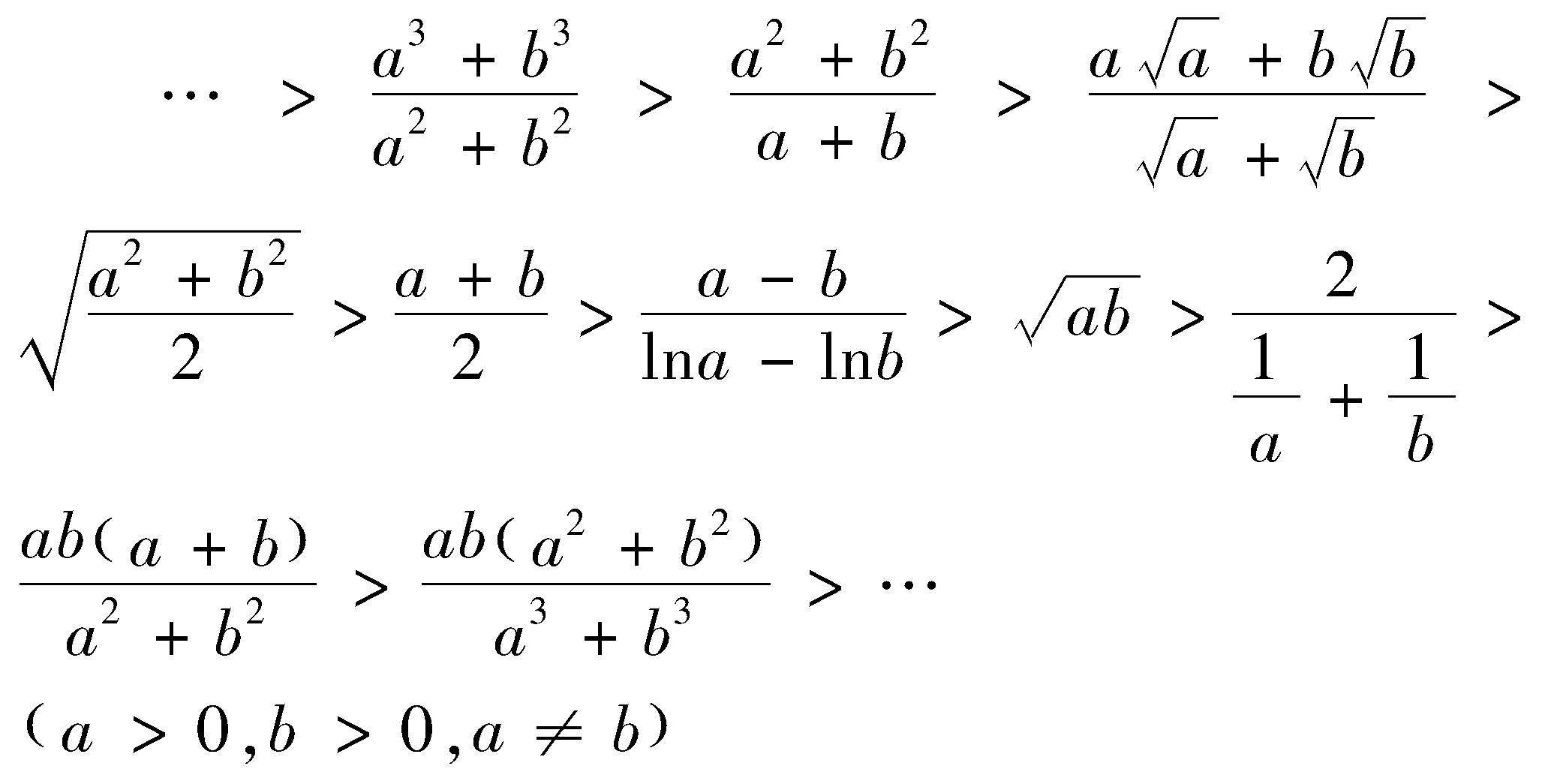
（苏教版必修1P70练习16）如图1，ABDC为梯形，其中AB=a，CD=b，设O为对角线的交点，GH表示平行于两底且与它们等距离的线段（即梯形的中位线），KL表示平行于两底且使梯形ABLK与梯形KLDC相似的線段，EF表示平行于两底且过点O的线段，MN表示平行于两底且将梯形ABDC分为面积相等的两个梯形的线段.试研究线段

因为线段EF经过对角线的交点，我们不妨称它为中心线.

MN表示平行于两底且将梯形ABDC分为面积相等的两个梯形的线段，故称其为等积线.

由此得到：等积线>中位线>相似线>中心线的有趣结论.

证略，由此加强为逆比线>等积线>中位线>相似线>中心线.

笔者最近尝试探究，发现基本不等式可以进一步加长，现与同行共勉.

上式不等式链用文字语言可表述为逆二次方比线>逆比线>逆根比线>等积线>中位线>相似线>中心线>顺二次方比线>顺三次方比线等.

若引入近几年较为流行的对数平均，我们又可当仁不让的得到以下不等式链：

参考文献

［1］顾旭东.对课本一个知识点的背景分析及变革延申〔J〕.福建中学数学，2023，（10）：12-14.