提出好的问题是问题教学的核心

马林刚

数学是问题的学科，提出问题、解决问题在解题的过程中往往起着关键作用，通过提出问题、解决问题，架设起已知和未知之间的桥梁.同样一个问题，从不同的角度进行分析、联想，建立不同的解题思路，会提出不同的问题，但落脚点都是解决问题.在教学中鼓励学生展示思考的成果，教师和学生一起提出问题、解决问题.不仅提高了学生的思维水平、表达能力，还丰富了学生解题体验，拓宽了解决问题的内涵，提升对数学问题的认知.本文以教学中处理一道习题的过程为例，谈提出好的问题在解决问题中的作用.

问题 （2022年全国高中数学联赛四川预赛试题第5题）已知函数f：{1，2，…，10}→{1，2，3，4，5}，且对一切k=1，2，…，9，有|f（k+1）－f（k）|≥3.则符合条件的函数f的个数为 .

分析：老师布置此题目作为课后思考题，给了学生充足的时间思考.讲解之初，由老师抛砖引玉.

一道看似很简单考察函数的定义的题目，似乎用列举就可以轻而易举的解决.但实际操作起来却发现很复杂，容易算错.

讲解之前教师提出三个问题：

（1）怎样化繁为简，研究出问题的本质，得到准确的答案？

（2）哪些数学解题思想在主导着解决问题的方向？

（3）此问题还可以怎样变形？

首先，直接列举：

虽然发现到了一些对解题有作用的性质：（1）f（x）≠3.若f（x）=3，f（x-1）或f（x+1）没有解.（集合{1，2，3，4，5}中最大的元素为5，最小的元素为1，|3－1|=|5－3|=2<3）f（x）的可能取值只能是集合{1，2，4，5}中的4个元素；（2）函数值随着自变量的改变呈现类似于周期性的性质；（3）考虑对题目做“退化”处理，研究f：{1，2，…，5}→{1，2，3，4，5}，或者研究f：{1，2，…，4}→{1，2，3，4，5}.

其次，教师再次提出问题：退化处理后发现解决确定函数的过程就是确定定义域内每个元素的象.但是题目要求并不是求出这些函数，而是求出符合条件的函数的个数，是否可以把这个周期性用得更宽泛？

这时想到的是从f（1）→f（5），f（5）→f（10）结果不够理想.于是列出表格：

继续进行讨论：当f（1）=1时，f（4）有2种时候等于4，有3种时候等于5；

当f（1）=2时，f（4）有1种时候等于4，有2种时候等于5；当f（1）=4时，f（4）有2种时候等于1，有1种时候等于2；当f（1）=5时，f（4）有3种时候等于1，有2种时候等于2.

继而得到： f（4）会出现5次1，3次2，3次4，5次5.对于f（7）而言，f（4）=1会产生5×2次4，5×3次5；f（4）=2会产生3×1次4，3×2次5；f（4）=4会产生3×2次1，3×1次2；f（4）=5会产生5×3次1，5×2次2.共有21次f（7）=1，13次f（7）=2，13次f（7）=4，21次f（7）=5.对于从f（7）到f（10），f（7）=1得到f（10）有21×5种情况，f（7）=2得到f（10）有13×2种情况，f（7）=4得到f（10）有13×3种情况，f（7）=5得到f（10）有21×5种情况.共计288种情况.

教师：这是本人的做法，解答比较繁杂，自己觉得成功之处在于分三步走，先退化到简单情形，本来想两步解决，但列举时发现可以分三次走更轻松.个人觉得没有把题目蕴含的本质搞清楚，只看到了问题的一面.对题目的本质局限在函数的定义，没有找到更好的数学模型.

教师提出问题：本题还可以做什么样的推广和拓展？

学生甲：我先证明一个引理：从左至右m个位置（m≥2n+1），n个相同的元素放在m个位置，要求这n个元素互不相邻，有Cnm－n+1种放法.

因为n个元素要占用n个位置且不相邻，所以需要用m－n个座位来隔开这n个元素，于是出现m－n+1个空格（因为两端各有1个，中间有m－n－1个），n个元素在这m－n+1个空格种选择，因为不分彼此，所以有Cnm－n+1种放法.

这对于本题有什么作用呢？我们先来看一种特殊情形：5 1 5 1 5 1 5 1 5 1 .

现在5的位置可以用4替换，1的位置可以用2替换，但是相邻的两个数不能同时被替换，那样就不满足|f（k+1）－f（k）|≥3.而 1 5 1 5 1 5 1 5 1 5 的情況与之类似，故总的对应有2（C010－0+1+C110－1+1+C210－2+1+C310－3+1+C410－4+1+C510－5+1）=2（C011+C110+C29+C38+C47+C56）个.

教师：甲同学的解答重在建立了一种可靠的模型，比我的做法简单很多，值得借鉴，把不熟悉的问题通过建立模型转化到熟悉的场景下解决是常用的方法.给甲同学掌声鼓励.

教师再次提出问题：（1）可以用有限归纳的方法来讨论吗？（2）如果用有限归纳的方法讨论是不是不严谨？（3）怎么处理这个不严谨的问题？

我发现乙同学的做法很有趣，他回答了问题（1），下面请乙同学在黑板上板书讲解.

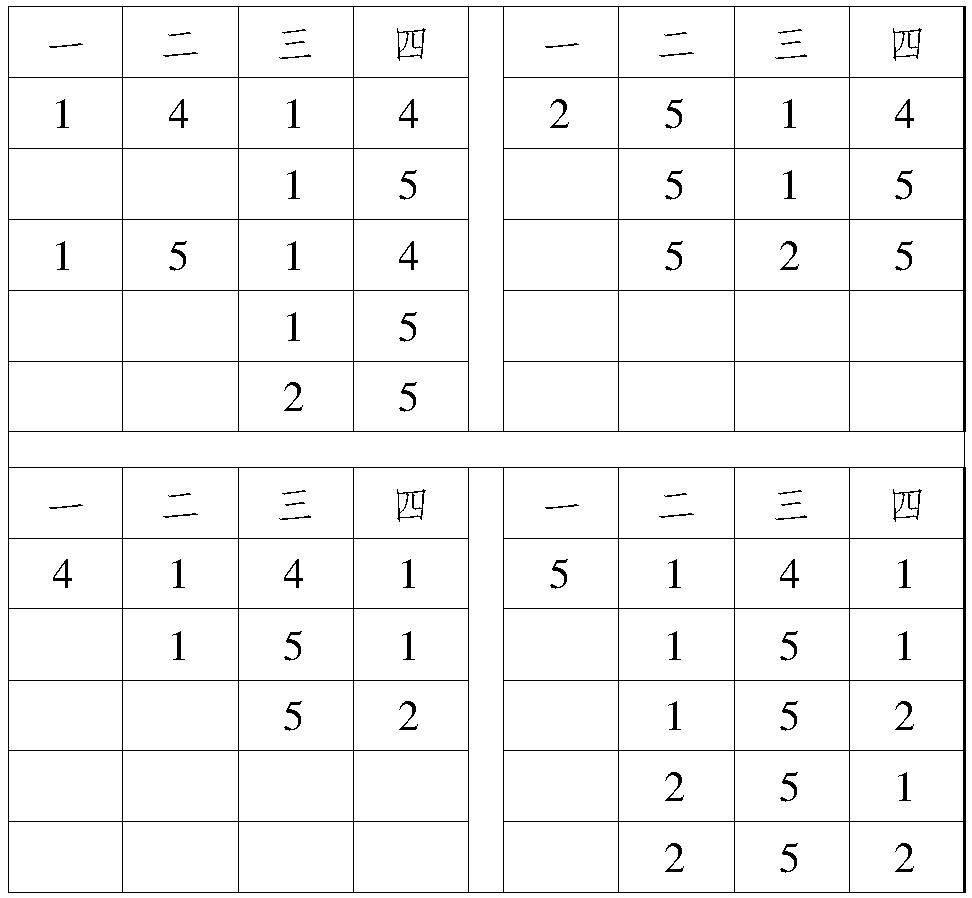
乙同学：我也是列举了一个树状图，不过是以对应的种数来列的，结果好象出现了斐波那契数列.首先：确立如右的对应，建立这样的对应是基于1和5有相同的属性，就是对应的元素可以有两种情形，如f（k）=1，则f（k+1）=4或者5；f（k）=5，则f（k+1）=1或者2；而如果f（k）=2，则f（k+1）=5；f（k）=4，则f（k+1）=1.于是A→B或A，而B→A.

经过有限归纳，我猜想：接下来是

当f（1）=1或者2时，情况一样，也是144种，所以共有288个对应.如下所示.

教师：乙同学做得很棒，如果能够给后面的推导有个更加严格的说明就好了.有没有同学想好的？

丙同学：还是针对黑板上的情况，我们分析f（k）=ak，{an}满足斐波那契数列，就是要满足：①a1=a2=1，②n≥2时，an+1=an+an－1.显然①满足，对于②，f（k－1）出现了x个A，y个B，即an-1=x+y.则f（k）出现了x+y个A，x个B，即an=（x+y）+x；于是f（k+1）出现了x+（x+y）个A，x+y个B，即an+1=x+（x+y）+（x+y）=3x+2y=an－1+an.

教师：谢谢丙同学给出了相对严格的证明.乙同学借助斐波那契数列的模型解决了问题，丙同学的分析也很科学.本题的求解中对于条件的简化与假设都是值得学习的，这就是去伪存真，抓住本质的过程.希望同学多思考，多总结，多交流，把学习数学、深化问题解决越做越好.感谢三位同学的精彩分析.

课后记：纵观三种做法，乙同学的做法在得到丙同学的严格证明后不失为最接近本质的做法，甲同学借助的排列组合知识值得肯定，只有老师的做法显得不够精巧，说明同学们的思维非常开放而又灵活，值得表扬.合理联想，建立契合题目的数学模型，是今后解决问题中应该有意考虑的问题.