借助迁移式问题链 构建运算的一致性

冯佳美

【摘   要】《义务教育数学课程标准（2022年版）》在“数与运算”主题中明确指出，要让学生“体会数的运算本质上的一致性”。在教学“小数四则运算的再认识”这一内容时，教师以核心内容“计数单位统领小数四则运算的一致性”为统领，以问题链为抓手，设计了“关联加减、迁移乘法、类比除法”的迁移式问题链，以建立小数加、减、乘、除法之间的联系，帮助学生理解“数的运算”的核心本质，感悟运算的整体性与一致性，从而培养学生的运算能力、推理意识和模型意识。

【关键词】迁移式问题链；运算的一致性；小数四则运算

《义务教育数学课程标准（2022年版）》在“数与运算”主题中指出，要让学生“感悟数的运算以及运算之间的关系，体会数的运算本质上的一致性，形成运算能力和推理意识”。然而，五年级学生在学完小数四则运算后，对四则运算的理解往往是孤立的，缺乏对小数运算算理一致性的全面认识。

从教材的编排情况来看，在小数加减法的学习中，学生受整数加减法正迁移的影响，能够较好地理解并掌握小数加减法的运算意义。然而，在小数乘除法的学习中，教材并未结合小数乘除法的运算意义展开教学，而是引导学生依据积的变化规律和商的变化规律，将其转化为整数乘除法进行运算。这在一定程度上强化了学生对算法的掌握，弱化了学生对算理的理解。因此，引导学生建立小数加、减、乘、除法之间的联系，融通算理与算法，整体构建运算的一致性，成为教学中的重要内容。

问题是教学的核心，也是推动学生思维发展的关键因素。在教学中，教师可以通过设计问题链，有效支持学生经历数学知识的形成与建构过程。在教材中小数四则运算相关内容教学结束后，笔者设计了“小数四则运算的再认识”这一教学内容，在核心内容“计数单位统领小数四则运算的一致性”的统领下，以问题链为抓手，设计了“关联加减、迁移乘法、类比除法”的迁移式问题链。通过问题链帮助学生建立小数加、减、乘、除法之间的联系，深化学生对运算整体性与一致性的理解，从而培养学生的运算能力、推理意识和模型意识。

一、聚焦核心内容：计数单位统领小数四则运算的一致性

核心内容体现了数学学科本质，有助于揭示知识间的内在联系，具有很强的迁移价值。因此，深入理解与把握核心内容，能够帮助学生将零散的知识点串联起来，形成知识网络，从而实现知识与方法的迁移应用。那么，运算一致性的核心内容是什么？对此，史宁中教授指出：数的建构与数的运算都是基于计数单位进行的，所有的运算都是相同计数单位个数的变化。加法是计数单位个数的合并，减法是计数单位个数的拆分，乘法是计数单位个数的累加，除法则是计数单位个数的递减。因此，运算一致性的核心内容就是计数单位。

（一）计数单位如何统领小数加减法？

在进行小数加减法运算时，首先要统一计数单位，然后再计算计数单位的个数。例如，在计算小数加法0.42+0.3时，可以将其看作“4个0.1加3个0.1加2个0.01”，结果为“7个0.1加上2个0.01”。但这种表示方式不能直观显示计数单位的个数，故教师可以将计数单位统一为更小的单位，如0.01，把加法运算变为“42个0.01加30个0.01”，结果得到“72个0.01”。减法运算同理。如0.42-0.3可以看成“42个0.01减30个0.01”，结果为“12个0.01”。因此，在计数单位的统领下，小数加减法的运算体现为计数单位不变，计数单位的个数相加减。

（二）计数单位也可以统领小数乘除法吗？

在小数乘除法运算中，计数单位相较于小数加减法有所变化。具体表现为：在进行小数乘法计算时，如计算0.2×0.3，可先将其转化为“（2×0.1）×（3×0.1）”，再简化为“（2×3）×（0.1×0.1）”，最终得到“6×0.01”。在这一过程中，新计数单位通过两个原计数单位相乘得到。在进行小数除法计算时，如计算0.06÷0.3，可先将其转化为“（6×0.01）÷（3×0.1）”，再简化为“（6÷3）×（0.01÷0.1）”，最终得到“2×0.1”。这里的计数单位则是通过两个原计数单位相除得到。尽管小数乘除法的计数单位有所变化，但其核心依然是围绕计数单位的个数进行计算。无论是乘法还是除法，都可以归纳为“计数单位与计数单位进行运算，计数单位上的数字与计数单位上的数字进行运算”。

综上所述，以计数单位为核心内容教学小数乘除法，不仅可以使教学内容保持前后连贯，还能帮助学生整体建构对小数乘除法的理解。

二、提炼核心问题：小数四则运算一致性的迁移式问题链

郑毓信教授曾强调，“问题引领”的研究重点是“核心问题的提炼与加工”。教师应基于教材编排内容，立足实际学情，聚焦核心內容，精准提炼核心问题。在此基础上，对提炼的问题进行深度加工，形成问题链，以链条式结构为学生提供清晰的学习主线。在“小数四则运算的再认识”这一内容的学习中，教师以小数加法为学习起点，进一步设计“关联加减、迁移乘法、类比除法”的迁移式问题链，为学生的探究与迁移搭建支架（如图1）。

（一）关联加减，寻找一致性的“敲门砖”

在这一内容的学习之前，学生已掌握了小数加减法的运算意义。为此，教师从加法运算开始教学，先让学生借助“百格图”涂色表示“0.42+0.3”，再引导学生思考应如何表示“0.42+0.3”的涂色过程。是选择4个0.1加上3个0.1，再加上2个0.01，还是选择42个0.01加上30个0.01？大多数学生是选择42个0.01和30个0.01进行涂色的，因为在统一计数单位0.01后，可以直接看出计数单位的个数。由此得出，小数加法的算理是“求有几个相同的计数单位”。在此基础上，教师引导学生将这一学习经验顺向迁移至小数减法的算理表达上，以促进他们对小数加减法算理共性的深入思考。

有了加法运算的基础，学生在学习减法运算时表现出较高的水平。教师教学时，先分析学生的涂色作品，再让他们结合相应的算式进行表达。例如，0.42-0.3可以表示为“42个0.01减30个0.01，还剩下12个0.01”。接着引导学生思考发现：小数加减法之间的算理共性在于一致性，这也是整体建构的关键点。因此，核心问题“小数加减法之间有什么联系”成为将知识迁移到小数乘法的“敲门砖”。

（二）迁移乘法，打通一致性的“隔断墙”

小数乘法虽然和小数加减法一样，都表示“求有几个相同的计数单位”，但与小数加减法不同的是，原来的两个计数单位相乘会创生新的计数单位。因此，感悟乘法“计数单位的变化”就成为建构运算一致性的“隔断墙”。

在初步感悟“求有几个相同的计数单位”之后，學生自然会产生猜想：“小数乘法会不会也是在求有几个相同的计数单位？”于是教师引导学生计算0.2×0.3，并比较（2×3）×（0.1×0.1）与（2×3）×0.1两种结果，分析其计数单位是0.1还是0.01（即0.1×0.1）。根据计算结果0.06，学生能够准确判断出计数单位为0.01。但随之也会产生疑问：“为什么计数单位是0.01？”为此，教师引导学生通过“画一画”“找一找”“说一说”等活动，感悟小数乘法计数单位变化的原理。学生在充分探究后，通过与小数加减法算理进行比较，发现小数乘法的算理也是“求有几个相同的计数单位”，不同的是计数单位发生了变化，原来的两个计数单位相乘产生了一个新的计数单位。

（三）类比除法，巩固一致性的“顶梁柱”

“小数除法还是在求有几个相同的计数单位吗？”是本内容教学中的最后一个核心问题，也是建构运算一致性的“顶梁柱”。为此，教师基于先前对小数加减法、小数乘法的融会贯通，充分利用直观的微课，以帮助学生理解小数除法计数单位变化的原理。

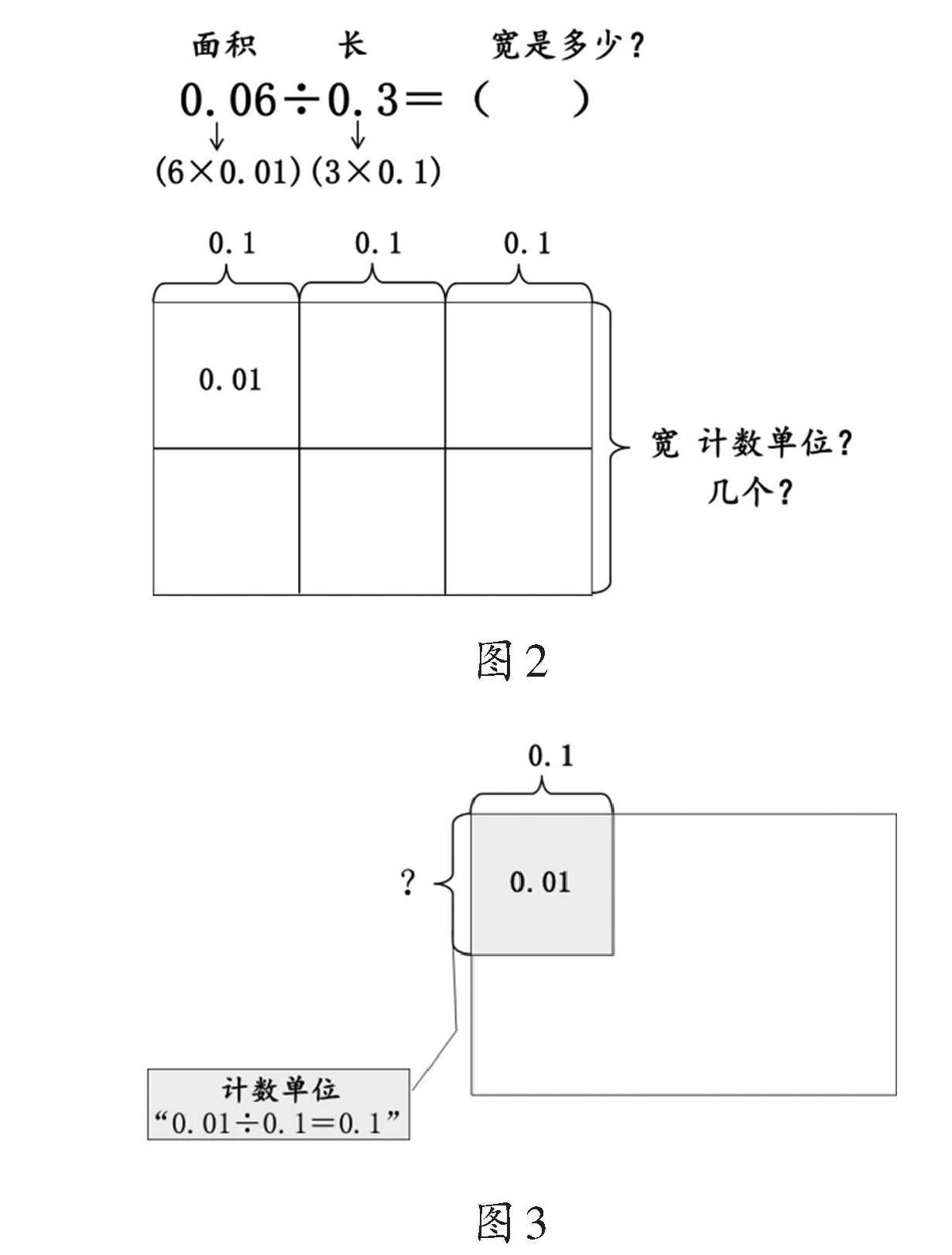
在教学0.06÷0.3的计算时，教师可以借助长方形的面积模型进行讨论。通过将0.06视为长方形的面积，0.3视为长方形的长，从而将0.06÷0.3转化为“已知面积和长，求宽是多少”的问题（如图2）。那么，算式0.06÷0.3就是在求“宽有几个这样的计数单位？”，即求宽这部分的计数单位是多少，以及有多少个这样的计数单位。确定宽这部分的计数单位个数，需要进行以下两个关键步骤：第一步，确定计数单位。由图3的涂色部分可知，正方形面积表示的计数单位是0.01。而长这部分的计数单位为0.1，故通过0.01÷0.1就可以求出宽这部分的计数单位，得到0.1。第二步，确定个数。长方形面积表示的计数单位有6个，其中一行有3个，可以排列成2行，由此可以得出0.1的个数为2个。最后，将求得的计数单位与个数相乘，就可得出宽为2个0.1。在上述师生讨论的基础上，教师再利用动态的微课进行讲解，帮助学生进一步理解小数除法计数单位变化的原理。

迁移式问题链的教学是培养学生核心素养的重要抓手。教师应围绕核心内容，设计核心问题，并以序列问题链为教学路径，帮助学生建立知识与知识间的内在联系，从而推进学生对知识本质的深刻理解，促进学生思维的发展。

参考文献：

［1］中华人民共和国教育部.义务教育数学课程标准（2022年版）［M］.北京：北京师范大学出版社，2022．

［2］巩子坤，史宁中，张丹.义务教育数学课程标准修订的新视角：数的概念与运算的一致性［J］.课程·教材·教法，2022，42（6）：45-51，56.

［3］鲍善军，朱曙光.“一题一课”的教学价值、设计与策略［J］.教学月刊·小学版（数学），2022（7/8）：12-16.

［4］郑毓信.中国数学教育的“问题特色”［J］.数学教育学报，2018，27（1）：1-7.

（浙江省杭州市钱塘区云帆小学）