含剪切节理面岩质边坡滑裂面位置及稳定性研究
陈东宇 刘文连 眭素刚 许汉华

摘 要:同向双平面滑动是存在单一地质断层面(剪切节理面)岩质边坡的常见破坏模式之一,但对该种类型的滑裂面计算方法并不充足。为了能够更加高效准确地寻找边坡的滑裂面位置,判断边坡的稳定性,基于极限平衡理论和非线性数学规划模型,假设滑体的滑动方式为同向双平面滑动,再假设目标函数为该岩质边坡的安全系数,运用MTALAB全局最优搜索法,计算含剪切节理面工程边坡在天然工况作用下的滑裂面位置及稳定性,并与极限分析法、强度折减法和毕肖普法进行对比分析。研究结果表明:基于极限平衡理论和非线性数学规划模型得出的滑裂面位置与安全系数基本一致,验证此类方法的可行性,为存在单一地质断层面岩质边坡的滑裂面计算和稳定性分析提供了新依据。
关键词:岩质边坡;滑裂面计算;安全系数;极限平衡法;非线性理论;最优化原理
中图分类号:TU452
文献标志码:A
岩质边坡的地层是分布在我国西南地区的一种工程性质较差的软岩,从上世纪60年代国家开始对西南地区进行开发建设,岩质边坡就慢慢地出现在工程作业中。在工程作业中,滑坡等地质灾害就出现在了我们的视线当中,其不仅制约了工程建设的发展,而且还对人类的生产生活产生了许多影响[1-2]。针对这一特殊的软质岩土,预测边坡稳定性及滑坡失稳面的位置,对土建、水利、交通等方面有非常重要的意义。
在结构面控制型边坡中,主要的失稳模式有平面滑动、楔型滑动、倾倒破坏等[3-4]。目前常见的边坡稳定性预测分析方法有:极限平衡法、强度折减法、系统分析法、数值模拟等[5-8]。李芬[9]、朱擎[10]、程小龙[11]等通过强度折减法和双强度折减法解决了双平面破坏模式下的临界失稳问题,讨论了岩质边坡的破裂角和内摩擦角之间的关系,进而提出安全系数的简化估算公式。陈建宏等[12]使用了极限平衡分析的上下限法,并把模糊化处理参数和置信水平等概念加入到了平面滑动的岩质边坡工程中,此方法能够有效地解决平面滑动岩质边坡的参数不确定问题。CHENG[13]、ARDESTANI[14]等采用极限平衡法,通过二维平面应力分析求解边坡的临界滑动面及稳定性系数。SCHLOTFELDT等[15]以反倾岩质边坡为研究对象,把数值分析与极限平衡法相结合,提出了这类岩质边坡的研究方法。张崇波[16]对香港秀茂坪岩质边坡进行了可靠性分析,利用拉丁超立方抽樣可靠性分析方法,分析了同时考虑参数不确定性和最危险滑面不确定性的平面滑动岩质边坡可靠性,优化了可靠性分析方法的计算精度和效率,将研究成果应用到工程实践,并将该方法应用到山东临沂换流站站址边坡的评价当中。陈志强等[17]提出了如果岩质边坡的滑裂面位置和产状无法确定,就可以用岩质边坡平面滑动滑面极限倾角来计算边坡的最小安全系数,并考虑拉裂缝深度对滑坡稳定性的影响。高丙丽等[18]基于坐标投影法,提出了三维单滑面和双滑面型块体的稳定系数计算方法,并基于Matlab开发出适于岩质边坡工程中平面多面体块体和曲面块体稳定性分析的CPG程序,实现了结构面、临空面及不稳定块体的空间表示及可视化。但对存在剪切节理面岩质边坡的滑裂面位置的计算除了工程软件外,并没有其他更加简便的方法了。
针对以上研究的不足之处,本文以两种不同地层的岩质边坡为研究对象,将极限平衡理论和非线性数学规划理论结合起来,通过求解最优化方法确定安全系数从而求解岩质边坡滑裂面,建立一种直接计算同向双平面滑动边坡滑裂面位置的计算方法。
1 计算原理
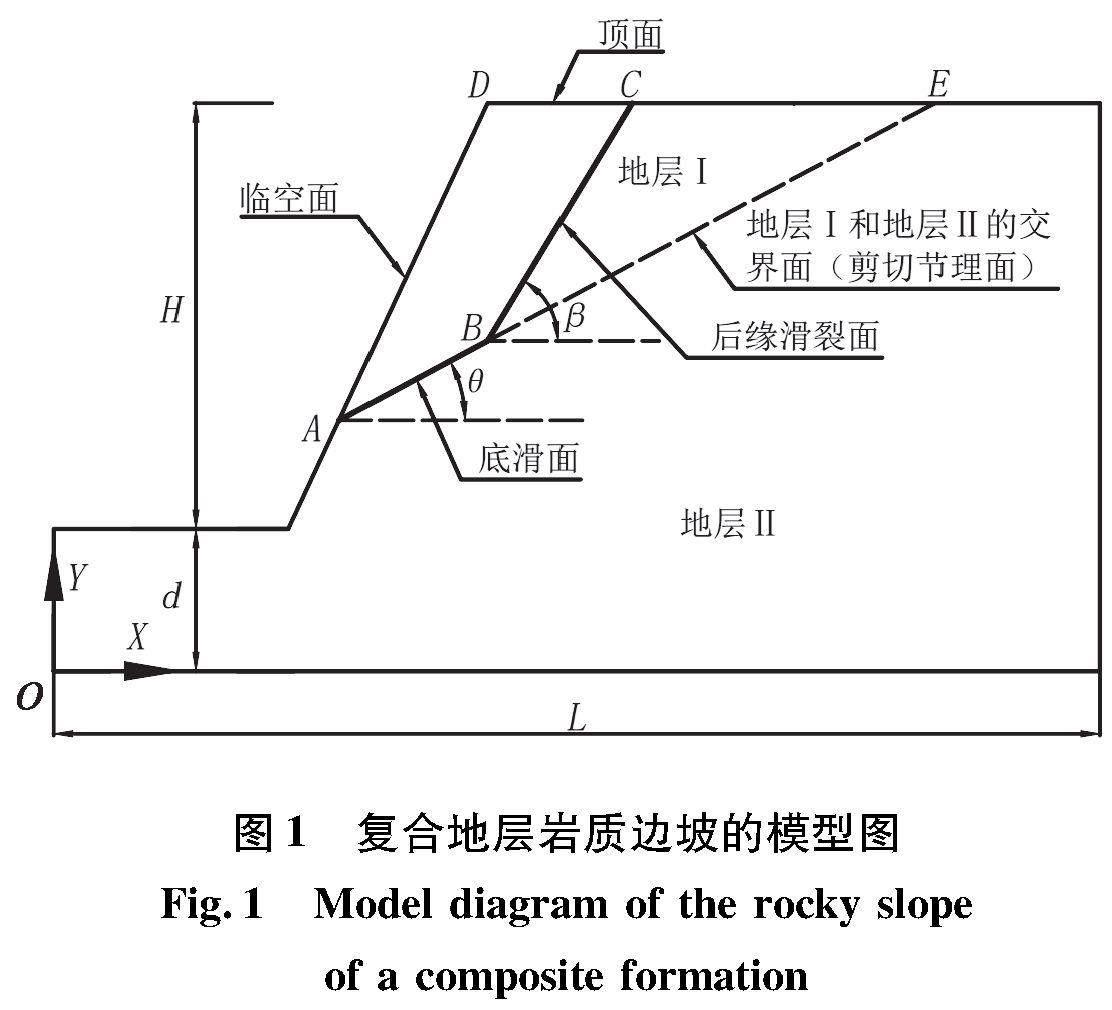
对于稳定性受确定性结构面控制的岩质边坡,应根据结构面的产状与强度参数,采用极限平衡方法计算边坡的稳定性。根据结构面的空间展布,边坡失稳类型分别为平面滑动和空间滑动。严格意义上边坡滑体都是空间块体,但对于单一结构面控制的滑体,或由两个及两个以上平面构成的画面,只要这些平面走向大致相同、与边坡破面走向平行或接近平行,且滑体两侧不受约束或约束不大时,即可按平面滑动进行分析,即本文算法的基本原理。如图1所示,本文研究对象主要是存在两种不同地层的复合岩质边坡,该类边坡主要是由于不同纪元产生的不同类型岩石共同组成的一种特殊的复合地层岩质边坡,地层Ⅱ的强度较大,其次是地层Ⅰ,该岩质边坡强度较弱的部分即最容易发生滑裂的部位是两种地层的交界面(剪切节理面),通常的破坏形式为同向双平面滑动。传统计算方法常见的有有限元法、强度折减法、极限平衡法,可通过工程软件大量的计算来实现,但计算结果通常为圆弧型滑裂面或为不规则滑动面,不符合边坡实际滑裂面形状。
本文算法基于塑性力学的基本理论,将边坡安全系数作为目标函数,将底滑面和后缘滑裂面的位置坐标作为决策变量,同时考虑滑体非线性约束,如极限平衡方程,底滑面、后缘滑裂面的屈服条件,即Mohr-Coulomb屈服条件,最后使用优化算法可同时求解得到边坡的安全系数及底滑面和后缘滑裂面控制点的位置坐标。
2 边坡滑块计算模型
将边坡滑块离散出来成为一块状单元如图2所示,该块体单元为一四面体,每条边为一结构面,除了该单元体的自重,底滑面和后缘滑裂面还受到法向力和剪力;由于已有极限平衡法里的刚性假设,该滑体的内部不会发生变形,故可以直接对该滑体进行受力分析。该滑块单元的受力如图2所示,滑块在形心处受到自身重力G,θ为两种地层交界线(底滑面)与水平方向的夹角,β为后缘滑裂面与水平方向的夹角,由于不施加外部荷载,故临空面AD和顶面CD是不受力的,滑块底滑面AB受到支持力NAB和剪切力SAB,后缘滑裂面也受到支持力NBC和剪切力SBC,此时该滑块单元处于极限平衡状态。
3 岩质边坡的力学机制分析
3.1 滑块的力学模型及几何关系
根据含剪切节理面的岩质边坡变形破坏机制,可将发生破裂的面分为底滑面AB和后缘滑裂面BC两个部分,如图1所示,滑裂面、临空面和顶面共同组成滑块。
假设滑块为均质刚体,则滑块的非线性约束重力方程为
式中:G为滑体的自重;ρ为第四系地层的密度;g为重力加速度;(xA,yA)、(xB,yB)、(xC,yC)、(xD,yD)分别为A、B、C、D 4点的坐标。
3.2 底滑面和后缘滑裂面的几何关系
如图1所示,以O点为原点来确定A、B、C、D各点的坐标。
(1)底滑面AB的坐标及长度描述
式中:θ是底滑面AB与水平方向的夹角,θ以逆时针方向为正;xA是A点的x坐标,yA是y点的y坐标,xB是B点的x坐标,yB是B点的y坐标,lAB是底滑面AB的长度。
(2)后缘滑裂面BC的坐标及长度描述
式中:β是后缘滑裂面与水平方向的夹角,β以逆时针为正;xC是C点的x坐标,yC是C点的y坐标,lBC是后缘滑裂面BC的长度。
(3)后缘滑裂面BC两点的附加约束
式中:xD是D点的x坐标;L是岩质边坡的宽度;d是边坡基底的高度;H是岩质边坡的高度。其中,xB在xD和L之间取间隔为1。
3.3 含剪切节理面岩质边坡滑块的非线性数学规划模型
根据滑块的平衡方程、屈服条件和几何约束条件,可以建立约束非线性数学规划模型,由于约束条件较多,为了确保求解方程的可行性,本文采取最优化方法中的全局最优解。
(1)建立目标函数
Maximize K
式中:K为岩质边坡的安全系数;Maximize表示“使最大”。
(2)建立滑体的非线性约束平衡方程
式中:NAB是底滑面受到的法向力,NAB以受压为正;SAB是底滑面AB的剪力,SAB以对滑体产生逆时针的转动效果为正;NBC是后缘滑裂面BC的法向力,NBC以受压为正;SBC是后缘滑裂面BC的剪力,SBC以对滑体产生逆时针的转动效果为正。
(3)建立底滑面AB的非线性约束Mohr-Coulomb屈服条件
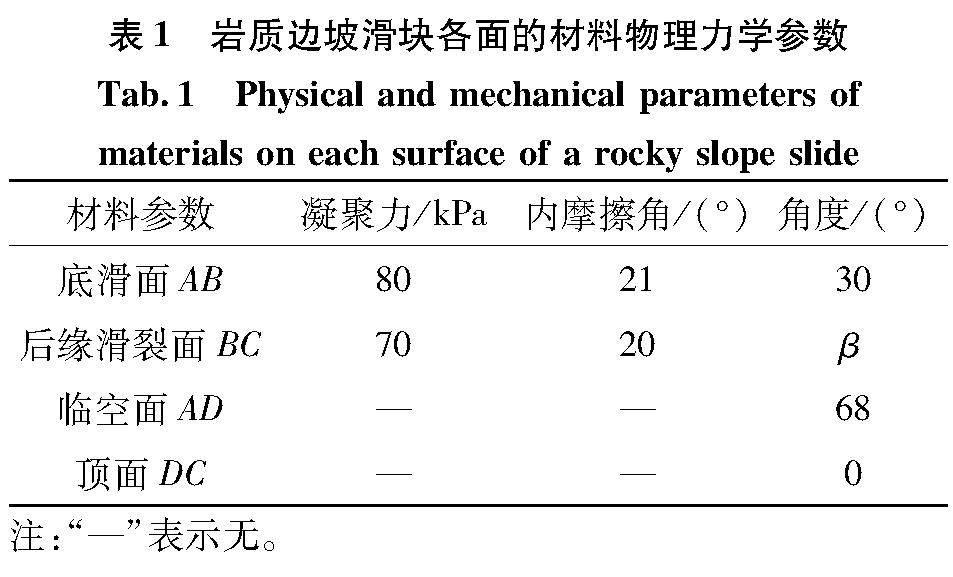
式中:K为岩质边坡的安全系数;NAB是底滑面AB受到的法向力,NAB以受压为正;SAB是底滑面AB的剪力,SAB以对滑体产生逆时针的转动效果为正;φAB是底滑面AB的内摩擦角;cAB是底滑面AB的凝聚力;lAB是底滑面AB的长度。
(4)建立后缘滑裂面BC的非线性约束Mohr-Coulomb屈服条件
式中:K为岩质边坡的安全系数;NBC是后缘滑裂面BC受到的法向力,NBC以受压为正;SBC是后缘滑裂面BC的剪力,SBC以对滑体产生逆时针的转动效果为正;φBC是后缘滑裂面BC的内摩擦角;cBC是后缘滑裂面BC的凝聚力;lBC是后缘滑裂面BC的长度。
(5)建立非线性数学规化模型
将上述目标函数安全系数K、滑块受力的极限平衡方程式、底滑面和后缘滑裂面的屈服条件式以及各点坐标的附加几何约束条件式联立,即可得到复合地层岩质边坡滑体的非线性数学规划模型如下:
上式中,部分参数可以在边坡中测量得知。
4 非线性数学规划模型的求解
岩质边坡后缘滑裂面位置稳定性计算方法的模型是一种比较典型的非线性数学规划模型,本文的模型计算流程如下。
(1)定义目标函数:定义滑面的材料参数,抗剪断凝聚力和内摩擦角度;定义几何、荷载参数,包括用几何法确定各点坐标和角度等确定部分并给予赋值,将未知部分作为未知数后续来进行求解。
(2)列出复合地层岩质边坡滑体的非线性数学规划的函数模型:先建立底滑面和后缘滑裂面的方程和滑体的重力计算公式;再根据上一步骤点的坐标确定底滑面lAB和后缘滑裂面lBC的长度;最后列出滑体的平衡方程和底滑面、后緣滑裂面的屈服条件以及部分额外几何平面约束。
(3)利用MATLAB软件中的功能函数进行求解,得到岩质边坡的安全系数K和后缘滑裂面BC的具体位置,即得到复合地层岩质边坡的后缘滑裂面位置的最优解。
5 基本算例分析
5.1 边坡算例参数
本文选取的岩质边坡具体参数为坡底宽L=100 m,坡高H=35 m,边坡基底高度d=15 m,边坡顶面宽度为67.19 m;临空面AD的倾斜角度为68°,底滑面AB的倾角为30°,边坡岩体的密度ρ=2 500 kg/m3,后缘滑裂面BC的倾角β为决策变量;对于滑体ABCD,其中,A点和D点坐标已知xA=19.920 8 m、yA=18.457 1 m、xD=32.806 2 m、yD=50 m,B点和C点坐标为决策变量。
在该算例中,由于滑块长期只受重力荷载的影响,故底滑面AB和后缘滑裂面BC的凝聚力和内摩擦角均为固定值,具体参数见表1。
5.2 本文算法的边坡算例计算结果
岩质边坡滑体的非线性数学规划模型是一个非线性数学规划模型,其目标函数是安全系数,使用全局最优解求解岩质边坡滑体的非线性数学规划模型,可求解得到以下决策变量:K、xC、β。其中,xB取坐标间距为1,根据xB的确定坐标求解得到的决策变量如表2所示。
由表2可以看出,MTALAB最优化算法,在以xB取间隔为1且能得到最优解的情况下得到的安全系数最小为0.791 7,即文本文算法最终结果。
5.3 本文算法结果验证
为了验证最优化算法求解最优滑裂面和安全系数的可靠性与和合理性,采用OPTUM G2 2020软件与Rocscience.Slide.v6007软件进行对比验算。本次验算通过算例选取模型进行建模并施加标准边界条件,选用OPTUM G2 2020软件中极限分析的上下限法及强度折减的上下限法进行滑裂面搜索,但搜索的滑裂面并非平面双折线型滑裂面,搜索得到的岩质边坡总位移如图3—6,图中红色实线为极限平衡最优搜索法结果,绿色多段线为软件搜索滑裂面,为了方便对比参考,将软件搜索的滑裂面取底滑面的右端点与滑裂面和顶面的交点的连线近似模拟同向双平面型滑裂面,即蓝色直线;选用Rocscience.Slide.v6007软件中的毕肖普法可以完成非圆弧滑裂面(平面双折线型滑裂面)的搜索,搜索得到岩质边坡的安全系数K,底滑面和后缘滑裂面的A点和B点坐标及后缘滑裂面倾角β如表3所示。
图3—6分别为G2软件通过极限分析和强度折减法的上下限法搜索的滑裂面位置,可以看出,G2软件搜索的滑裂面底滑面为直线形,但后缘滑裂面为近似圆弧形。在近似滑裂面与本文方法的结果滑裂面对比中,底滑面的长度误差在0.5 m之内,后缘滑裂面误差在1~2 m之间。从图中的安全系数对比,基于极限平衡法的最优化搜索的安全系数低于G2软件的各个方法所求的安全系数,最大差值为0.130 8,差距最小的是与极限平衡法的下限法的对比,误差为8.36%,差距最大的是与强度折减法的上限法的对比,误差为16.52%。通过对比近似滑裂面的倾角,极限平衡和强度折减法的上下限法与刚体平衡法的后缘滑裂面倾角相差3~4°,误差为5.09%~6.78%。
表3为毕肖普法与全局最优搜索法结果,从表3可以看出,本文的全局最优搜索法与Slide软件的毕肖普法搜索结果非常接近,誤差最大的依然为所计算的安全系数,误差为11.04%。对于滑裂面位置,通过两点坐标对比分析,误差最大的为B点x坐标,误差为5.88%,而C点坐标误差仅为0.60%。后缘滑裂面倾角毕肖普法得到的结果为56.71°,本文算法得到的结果为58.91°,误差为3.88%。
图7—9为毕肖普法与全局最优搜索法的结果,从图7—9可知,全局最优搜索法与Slide软件的毕肖普法搜索结果非常接近。两种方法的安全系数都随后缘滑裂面凝聚力c的增大而增大,在后缘滑裂面凝聚力c=120 kPa时差值最大,差值为0.176 3,误差为16.45%。对于滑裂面位置,通过两点坐标对比分析,B点x坐标在后缘滑裂面凝聚力c=85 kPa时差值最大,差值为2.84 m,但对一个100 m宽的边坡来说,误差仅为2.84%,而C点x坐标在后缘滑裂面凝聚力c=115 kPa时差值最大,差值为1.81 m,误差仅为1.81%。
5.4 结果分析与讨论
通过算例验证,我们不难发现本文算法的安全系数普遍偏低,相差最多为0.1左右,但在边坡防护治理工作中,可以起到预防边坡失稳的作用。由于计算方法和计算原理的不同,误差必然是存在的,在图3—7中我们可以发现极限平衡和强度折减的上下限法的滑裂面位置与本文算法搜索的滑裂面位置差距较大,这是因为OPTUM G2 软件无法实现同向双平面型滑裂面搜索,对于能够实现同向双平面型滑裂面搜索的Slide软件,毕肖普法与全局最优搜索法(本文算法)结果非常接近。
通过观察后缘滑裂面倾角,我们可以发现复合地层岩质边坡的后缘滑裂面倾角接近60°,根据边坡滑动破坏的普遍形式,平面滑动的边坡岩体是沿单一地质断层面(剪切节理面)的剪切位移,此时边坡倾角β、地层交界面倾角θ及其内摩擦角φ之间的关系为β>θ>φ。本文算法的实施例以及Slide软件的计算结果符合规定,进一步验证本文算法的可行性与正确性。
6 结论
(1)本文以复合地层岩质边坡为研究对象,基于非线性理论的非线性数学规划模型计算复合地层岩质边坡的稳定性及底滑面和后缘滑裂面位置,通过最优化方法中的全局最优搜索的计算结果,并与Slide软件的结果进行对比,验证了本文算法的可行性和准确性。
(2)传统的极限平衡法计算边坡的稳定性系数时,需要假定破坏面,然后再根据假定的每一个破坏面的安全系数,来确定边坡最易发生破坏的滑裂面,强度折减法对c、tan φ简单折减后得到的应力场已经不是原岩质边坡的真实应力场,故而得出的结果也存在偏差,而本文的方法可以省略滑裂面位置的假设,直接通过全局优化算出边坡的滑裂面位置,相比于极限平衡法,本文的编制程序更加简单、工程应用简便,可将其应用于含剪切节理面地层岩质边坡的设计中。
(3)计算边坡稳定性及边坡滑裂面的工程软件很多,主要以圆弧形滑裂面为主,但计算平面型滑裂面算法的软件还需开发,本文算法程序简单且计算精度较高,为同向双平面滑动的边坡提供了一种简单高效的计算方法。在本文算法中,边坡的滑裂面位置与Slide软件的计算结果非常接近,安全系数比软件的计算结果要普遍偏低,在工程应用中可以起到防范于未然的作用。
(4)本文提出了一种用于特殊岩质边坡折线形滑裂面分析的计算方法,旨在解决现有软件如OPTUM G2和Madis civil在处理此类问题时的不足。所开发的计算程序具有简单直观、原理明确且计算精度高的特点。本方法理论基础扎实,且在工程实践中操作简便,适用于处理含有单个地质断裂面(如断层面或剪切节理面)的岩质边坡的滑裂面位置分析。该算法不仅能够准确预测滑裂面的位置,还能清晰地展示滑块的自重、底部滑动面和后缘滑裂面的受力状况,从而直观地呈现边坡的稳定性状况。此外,算法提供的详细信息对于边坡支护结构的设计同样具有重要价值。
参考文献:
[1]黄润秋. 20世纪以来中国的大型滑坡及其发生机制[J]. 岩石力学与工程学报, 2007(3): 433-454.
[2] 夏元友, 李梅. 边坡稳定性评价方法研究及发展趋势[J]. 岩石力学与工程学报, 2002(7): 1087-1091.
[3] 杨肖锋, 鲁祖德, 陈从新, 等. 板裂结构顺层岩质边坡滑移-弯曲破坏机制的力学模型研究[J]. 岩土力学, 2022, 43(增刊1): 258-266.
[4] 黄少平, 晏鄂川, 尹晓萌, 等. 不同临空条件的层状反倾岩质边坡倾倒变形几何特征参数影响规律[J]. 地质科技通报, 2021, 40(1): 159-165.
[5] LUO G, HU Q, TAN J. Process stability analysis for high slope based on limit equilibrium method and strength reduction finite element method[J]. Mining and Metallurgical Engineering, 2013, 33(2): 14-17.
[6] YAN L, SUN Y. The analysis on rock slope stability based on strength reduction technique[J]. Journal of Guangxi University(Natural Science Edition), 2008, 33(3): 235-238.
[7] 张文莲, 孙晓云, 陈勇, 等. 基于岩体抗压强度折减的边坡稳定性分析方法[J]. 岩土力学, 2022, 43(增刊1): 607-615.
[8] 李宁, 郭双枫, 姚显春. 再论岩质高边坡稳定性分析方法[J]. 岩土力学, 2018, 39(2): 397-406,416.
[9] 李芬, 成涛. 基于双折减系数法的岩质边坡平面滑动分析[J]. 公路工程, 2018, 43(5): 294-299.
[10]朱擘, 何光春. 强度折减法在平面滑动型岩质边坡的应用[J]. 水运工程, 2012(9): 65-69.
[11]程小龙, 张绪进, 朱擘. 双强度折减法在平面滑动岩质边坡中的应用[J]. 水运工程, 2013(3): 72-76.
[12]陈建宏, 钟福生, 陈定坤. 平面滑动型岩质边坡极限平衡分析的上下限法[J]. 中南大学学报(自然科学版), 2013, 44(8): 3310-3315.
[13]CHENG Y, LANSIVAARA T, WEI W. Two-dimensional slope stability analysis by limit equilibrium and strength reduction methods[J]. Computers and Geotechnics, 2007, 34(3): 137-150.
[14]ARDESTANI A, AMINI M, ESNAEILI K. A two-dimensional limit equilibrium computer code for analysis of complex toppling slope failures[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2021, 13(1): 114-130.
[15]SCHLOTFELDT P, ELME D, PANTON B. Overhanging rock slope by design: an integrated approach using rock mass strength characterisation, large-scale numerical modelling and limit equilibrium methods-ScienceDirect[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2018, 10(1): 72-90.
[16]張崇波. 基于LHS方法的岩质边坡平面滑动可靠性分析[D]. 南京: 南京大学, 2015.
[17]陈志强, 王亮清, 刘顺昌. 岩质边坡平面滑动滑面极限倾角的研究[J]. 人民长江, 2013, 44(13): 39-42.
[18]高丙丽, 李铎, 李朗, 等. 基于坐标投影法岩质边坡块体稳定性分析及其可视化研究[J]. 岩土力学, 2022, 43(1): 181-194.
Study on the Location and Stability of Slip Fracture Surface
of Rocky Slope with Shear Joint
Abstract:
Codirectional biplane sliding is one of the common failure modes of rock slopes with a single geological fault plane (shear joint face), but the calculation methods for this type of slip surface are insufficient. In order to find the position of the slip surface of the slope more efficiently and accurately, and judge the stability of the slope, based on the limit equilibrium theory and nonlinear mathematical programming model, assuming that the slider has fallen off and the shape is an uncertain quadrilateral slide, and then assuming that the objective function is the safety factor of the rock slope, the position and stability of the slip fracture surface of the engineering slope with shear joint surface under natural working conditions are calculated by using MTALAB's global optimal search method. Then the results are analyzed and compared with those ofthe strength reduction method and the Bishop rigid body equilibrium method. The results show that the position of the slip fracture surface based on the limit equilibrium theory and the nonlinear mathematical programming model is basically consistent with the safety factor, which verifies the feasibility of such a method, providing a new basis for the calculation and stability analysis of the slip fracture surface of rock slope with a single geological fault layer.
Key words:
rock slope; calculation of slip surface; safety factor; limit equilibrium method; nonlinear theory; optimization principle
贵州大学学报(自然科学版)2024年3期
