基于可信执行环境的隐私保护认证人求交协议

喻朝新 雷琳琳 李丹 朱辉辉 凌国玮

摘 要：Ghosh等在NDSS 2023上首次提出了一种去中心化环境下用户建立信任机制的隐私保护认证人求交（private certifier intersection， PCI）协议。在PCI协议中，持有不同证书的双方能够计算出公共的认证人即证书中心（certificate authority， CA）集合，同时以隐私保护的方式验证这些认证人颁发的证书是否有效。PCI协议可用于解决去中心化环境下双方用户在没有先验的情况下建立相互信任机制的问题，但采用了复杂的安全多方计算方法导致效率不高，而且要求参与双方使用相同的签名算法，这在实际应用中是不合理的。针对这些问题，基于可信执行环境（trusted execution environment， TEE）提出一个新的PCI协议。所提协议采用TEE完成认证人求交过程且支持参与双方采用任意的数字签名算法生成证书，更具有实用性。实验结果表明所提协议在效率上明显优于Ghosh等的PCI协议。

关键词：隐私保护认证人求交；可信执行环境；签名；去中心化

中图分类号：TP309

文献标志码：A

在传统Web2.0中，个人隐私保护已成为人们日益关注的核心问题［1-3］。用户依赖有限的身份和服务提供商以及认证机构实现可信交互。然而，传统的证书认证存在着中心化、高费用、弱隐私性和高延迟等不足。

去中心化的Web3.0旨在增强用户自主创建、更新和选择性共享身份数据的能力，从而替换对集中式服务提供商的依赖，使用户能够证明关于自身的某个资质（或声明），而无需依赖集中式的联合身份提供商或权威可信认证人即证书中心（certificate authority， CA）集合［4］。

构建去中心化CA的一个挑战是如何在不同的用户之间建立信任机制。在去中心化系统中，证书的颁发是由多个CA完成［5-6］。若两个用户存在相同的CA，基于对CA的信任，双方能够成功建立起一个信任关系［7］。传统的解决方法是使用隐私保护集合求交（private set intersection，PSI）协议［8］进行双方CA集合的求交。PSI协议是一种在现实应用中被广泛使用的安全多方计算（multi-party computation， MPC）原语。在PSI协议中，参与方分别为发送者与接收者。协议开始时，发送者与接收者输入各自的私有集合。当PSI协议执行完成时，接收者可以得到双方集合的交集。在双向PSI协议中，双方都将得到交集。现有的高效PSI协议［9-11］几乎都是基于不经意传输扩展（oblivious transfer extension， OTE）［10］或者向量不经意线性评估（vector oblivious linear evaluation， VOLE）［12］構造的，其中最有代表性的高效PSI协议是KKRT协议［11］以及RR协议［13］。但是，在去中心化系统中，没有一个中央机构来管理和验证所有证书的合法性。因此，敌手可以伪造CA集合作为输入从而获得诚实参与方的全部或部分CA［14］。

针对以上问题，GHOSH等［15］在2023年信息安全国际顶级会议NDSS上提出隐私保护认证人求交（private certifier intersection， PCI）协议概念并说明了该协议能够很好地保护Web3.0中用户的隐私。PCI协议的输入是双方各自持有的证书以及颁发这些证书的认证人。PCI协议能够识别出双方的公共认证人集合，同时验证这些认证人颁发的证书是否有效，以防止恶意的参与方输入无效的证书和认证人。通过PCI，持有证书的双方可以在互不信任的情况下建立信任基础。PCI的提出为Web3.0中的用户提供了更强的隐私保护机制。

分析GHOSH等［15］的PCI协议，不难发现存在以下问题：

首先，在他们的PCI协议中，参与双方在MPC框架下完成证书的验签与求交，这种方法带来了巨大的计算开销，输入大小仅为1 000的PCI协议在局域网需要1.5 h以上。

其次，在现实应用中，不同的认证人往往会采用不同的数字签名算法（由认证人自身决定）。但是GHOSH等［15］的协议要求所有认证人都采用相同的签名算法。

在本文中，我们提出一种新的PCI协议。所提协议不仅能支持认证人使用不同的签名算法，而且相较于原始PCI协议［15］具有较大的性能优势，具体如下：

1）本文采用可信执行环境（trusted execution environment，TEE）［16］来规避计算开销极大的MPC验签过程，并基于现有抗恶意敌手的PSI协议［13］构造高效安全的PCI协议。

2）本文所构造的PCI协议支持认证人使用任意的签名算法，更符合现实应用需求。认证人只需将所采用的验签算法嵌入TEE即可。

3）本文通过实验与文献［15］进行效率对比。实验结果表明，所提PCI协议在输入集合大小为1 000时仅需1 s左右即可完成，相较于原始PCI协议具有较大的性能优势。同时，由于所提PCI协议支持不同的数字签名算法，本文还给出了使用ECDSA［17］、RSA［18］、SM2［19］这3种签名算法的实验结果。

1 预备知识

1.1 符号定义

本文令P1与P2分别代表PCI协议中的两个参与方。双方PCI协议的输入大小分别为N1与N2。令κ为计算安全参数，λ为统计安全参数。［a，b］表示从a到b的所有整数数值。［b］表示从1到b的所有整数。〈A，B〉表示2个向量A与B的内积。对于集合S，s←S指s是从S随机选取元素。V（pk，σ，m）=1表示对于任意的一个数字签名算法的验签算法V，输入公钥pk、签名消息m、数字签名σ，验签通过。令H1：{0，1}*→{0，1}κ，H2：{0，1}*→{0，1}κ/2。

1.2 可信执行环境

TEE［16］是一种安全计算环境，用于保护敏感数据和代码免受恶意软件和攻击者的侵害，保证程序初始状态和运行时的机密性、完整性。TEE提供了一种隔离机制，使得TEE内部的代码和数据能够与外部环境隔离开来，使得TEE外部的软硬件均无法获得其内部的机密信息。常见的可信执行环境包括硬件级别的Enclave（如Intel SGX）和软件级别的沙箱（如Google Chrome的沙箱）。TEE的安全性建立在多个方面的基础上，其中最重要的是隔离机制和加密保护。隔离机制确保敏感数据和代码只能被授权的程序和用户访问；而加密保护则用于保护数据的机密性和完整性。为了实现这些安全特性，TEE通常需要依赖于硬件支持和操作系统的协作。

TEE通常由特殊的硬件和安全操作系统组成。这些硬件通常包括安全处理器和特殊的存储器。在TEE中，所有执行代码和数据都必须经过认证和加密，只有经过身份验证和授权的用户才能访问TEE中的数据和功能。TEE还支持远程认证和安全通信，使得与TEE进行通信的其他设备可以验证TEE的身份和确保通信的安全性。在TEE中，所有执行的代码和数据都必须满足高度安全的要求，并且必须经过严格的测试和验证，以确保没有漏洞和后门。

1.3 向量不经意线性评估

向量不经意线性评估（vector oblivious linear evaluation， VOLE）［12］是构造高效MPC协议的重要基础组件。VOLE在MPC协议中起到的作用一般与著名的不经意传输扩展（oblivious transfer extension， OTE）协议等价［11］。在VOLE协议中有2个参与方P1与P2，当协议结束时，P1得到向量A，C，P2得到向量B、标量Δ，满足C=ΔA+B。目前高效的VOLE协议是由COUTEAU等［12］提出的Silver协议。本文所提的PCI协议也是基于Silver协议生成的VOLE向量。

1.4 不经意键值对存储

不经意键值对存储（oblivious key-value stores，OKVS）［12， 20-21］是由PINKAS等［21］提出的一种新型的键值对数据结构。设计它的初衷是为了替换PSI协议中的Cuckoo Hashing［22］，从而得到高效抗恶意敌手的PSI协议。此外，相比于Cuckoo Hashing，它需要更少的内存开销。OKVS按如下的方式被定义为一种键值对数据结构。

Encode （（x1，y1），…，（xn ，yn ），r）：给定键值对集合{（x1，y1），…，（xn，yn）}与随机数r←{0，1}κ，输出P∈{0，1}m，其中xi∈{0，1}，yi∈{0，1}，m≤1.3n。

Decode （P，xi ，r）：给定P，xi，r，返回yi。若存在row （xi ，r）→＼{0，1＼}m使得

Decode （P，xi ，r）=〈P，row （xi ，r）〉（1）

成立，則称OKVS为一个线性OKVS。令P是一个线性OKVS，设L是一个线性变换，且P=P′+P″，则线性OKVSP满足以下性质：

Decode （L（P），x，r）=L（Decode （P，x，r））

Decode （P，x，r）=Decode （P′，x，r）+Decode （P″，x，r）（2）

2 概念模型与协议模型

2.1 PCI概念模型

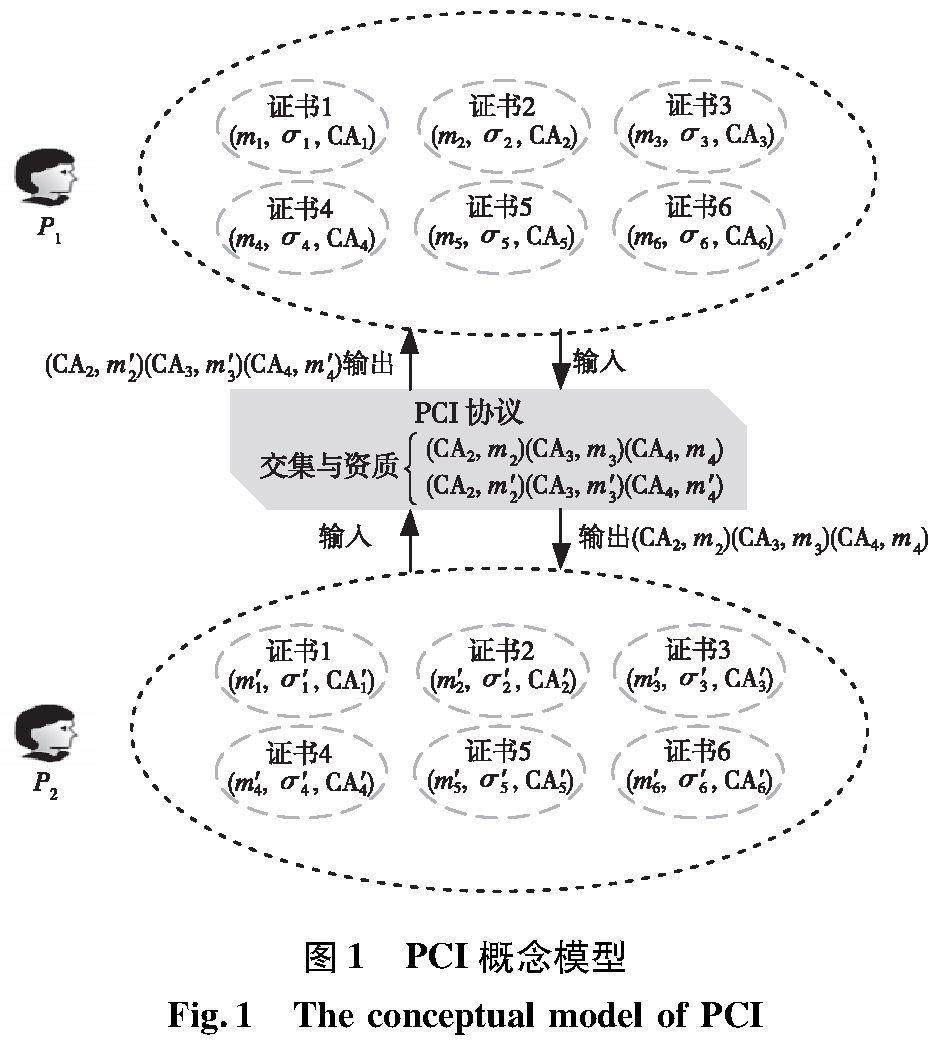
PCI是GHOSH等［15］提出的一种新的密码学原语。PCI概念模型如图1所示。参与方P1与P2拥有不同资质对应的证书以及CA。当Web3.0中的两方用户想要在去中心化的CA下建立信任机制时，双方以各自证书以及CA作为PCI协议的输入，最终双方各自得到一个共有的CA交集以及CA对应的资质，且不在交集内的CA在求交验证过程中完全不会暴漏。如果泄露了不在交集内的CA，则会给Web3.0中的用户造成额外的隐私泄露问题。在图1中，mi和m′i不一定是同一种资质，只要用户双方就某个相同或不同资质具有共同的CA达成一致即可。

2.2 PCI协议定义

在本协议中，参与方Pi，i∈{1，2}分别拥有私密输入pi，1={pki，j，σi，j，mi，j}与公开输入pi，2={m′i，j}，其中：pki，j为数字签名σi，j执行验签算法所需要的公钥（代表验证人身份）；mi，j为σi，j所对应的签名消息（在PCI协议中为参与方Pi想证明的某个资质或属性）；pi，2为Pi想要证明的所有资质或属性集合。

当PCI协议执行结束时，Pi得到输出：

I={I1={pk′j}，Ii，2={m′k}（3）

在输出I1中，满足任意pk′j∈{{pk1，j}∩{pk2，j}}且存在V（pk′j，σ1，j ，m1，j）=V（pk′j，σ2，j，m2，j）=1成立。在Ii，2中，对于P1，任意m′k∈p2，2且存在pk′j∈I1使得在p2，1中存在V（pk′j，σ2，j ，m′k）=1。对于P2，满足任意m′k∈p1，2且存在pk′j∈I1使得在p1，1中存在V（pk′j，σ2，j ，m′k）=1。

简单的说，在PCI协议中，Pi会得到能够让数字签名验签通过的公钥交集（通过该公钥交集确定认证人的身份）。同时，Pi也会得到对方的有效资质（被双方共同信任的认证人所认证）。

2.3 安全性定义

在理想-现实范式下［23］，敌手可以攻破P1与P2的任意一方。为了便于描述，在此处P1为恶意方（被敌手所攻破的一方），P2为诚实方。

PCI的理想功能（FPCI）如下所示。

1） 参与方Pi输入pi，1={pki，j，σi，j，mi，j}与 pi，2={m′i，j}。P2直接向FPCI提供它的正确输入，P1的输入由模拟器S提供。

2） FPCI计算PCI协议的输出I={I1，Ii，2}。

3） FPCI发送{I={I1，I1，2}，N1，p1，2}给模拟器S。

4） 若S要求FPCI中止协议，则FPCI协议终止。

5） 若S不要求FPCI终止，则FPCI分别发送I={I1，Ii，2}，N1，N2给P1与P2。

现实世界。P2从环境Z中得到自身的输入，并诚实地执行PCI协议。敌手A控制P1与P2和Z进行交互。Z为P2提供输入的同时也会得到P2的输出。

理想世界。P2从环境Z中得到自身的输入，并作为FPCI的输入。模拟器S代表P1向FPCI发送其输入，并从FPCI得到对应的输出。S也会与Z进行交互，旨在使理想世界中的交集与真实世界中的交集计算不可区分。Z为P2提供输入，并与模拟器S进行交互，也会得到P2的输出。

对于一个任意的PCI协议，给定任意的敌手A，环境Z，模拟器S，可以定义以下随机变量。

real A，Z 表示Z与敌手A在真实世界中交互执行PCI协议所能得到的一切视图，包括其输入、输出、过程中收到的消息、随机带。

idealA，Z表示Z与模拟器S在理想世界中交互执行PCI协议所能得到的一切视图，包括其输入、输出、过程中收到的消息、隨机带。

定义1（安全的PCI协议） 给定安全参数κ，对于任意的概率多项式敌手A与概率多项式环境Z，存在一个模拟器S使得

3 基于TEE的高效PCI协议

3.1 研究动机

在实际应用中，不同用户和应用场景的需求是不一样的，从而导致涉及的签名算法、证书类型以及性能要求也各自不同。例如，个人笔记本电脑中存有基于多种签名算法的数字证书，如图2和图3所示。此外，随着Web3.0中数字身份的日益普及和信息交流的频率不断增加，确保隐私保护认证人求交的速度变得尤为重要。在通信双方频繁进行认证人求交的背景下，证书数量的增加可能会导致求交过程变得较为缓慢，甚至可能造成敏感信息泄露的风险。因此，设计出一种能够支持灵活签名算法且安全高效的PCI协议以满足这些多样化的需求，变得尤为迫切和重要。

3.2 协议框架

本文协议框架如图4所示。P1和P2以各自认证人即公钥pk、证书σ、资质m为输入，在TEE中执行证书的验签过程。将验签算法通过的认证人与声明存入TEE的临时安全内存M1和M2中。双方以各自认证人集合X与Y为输入执行一个抗恶意敌手的PSI即VOLE协议，直到P2生成掩码集合Y′。P2将掩码集合Y′输入TEE。P1将认证人集合X：={x}输入TEE，并在TEE中进行掩码集合X′的生成。然后TEE判断x∈X′∩Y′是否成立。若成立，则进一步判断x是否在验签算法通过的临时安全内存中。若x存在于临时安全内存中，则TEE将求得的交集列表{I1，I1，2}发送给P1，{I1，I2，2}发送给P2。

此外，在协议框架方面，我们采用TEE代替原始PCI协议的MPC框架［15］，从而实现高效、安全、灵活性高的PCI协议。

3.3 协议构造难点

构造PCI协议的关键是如何在没有可信第三方情况下安全地执行验签算法。如果能够高效且安全地完成双方证书的验签，那么就能够结合一个高效且抗恶意敌手的PSI协议，成功构造出PCI协议。那么该如何替代计算开销较大的MPC验签过程？以下有一种看似合理的简单结合方法：首先双方借助TEE执行合法验签过滤错误输入，然后执行一个抗恶意敌手的PSI协议。

但是，上述方法存在以下问题：TEE执行签名流程结束后，参与方Pi仍然无法过滤掉对方的错误输入。因为Pi无法获取对方的签名结果，毕竟有些通过验签的合法输入不一定在交集中。如何克服这一问题是将TEE与恶意PSI协议结合形成PCI协议的关键。因此，在新的PCI协议中，我们必须更加细致地设计PCI协议的具体流程以保证参与方Pi隐私不会泄露。

本文结合TEE与现今高效的恶意PSI协议［13］构造一个新的安全高效的PCI协议。该协议不仅不会有以上朴素的结合方法带来的隐私泄露问题，而且相较于GHOSH等的PCI协议［15］具有效率更高的优势。此外，因为每个用户选择的证书颁发机构采用的签名算法是不统一的，该协议支持认证人在一次PCI协议中使用任意签名算法，更加符合现实Web3.0中的应用场景。

3.4 协议概述与技术细节

为了用户双方能够安全且成功地执行PCI流程，分别介绍所使用的恶意PSI协议［13］以及TEE的具体功能。

3.4.1 PSI协议

首先，参与方Pi执行一个VOLE协议［12］，P1得到向量A，C；P2得到向量B与标量Δ满足C=ΔA+B。然后，设向量P是{x，H2（x）}的线性OKVS。P1发送A′：=P+A给P2，P2随后计算B′=B+ΔA′。因此，P1与P2安全地将VOLE输出（A，B，C，Δ）转化为（P，B′，C，Δ），满足C=B′－ΔP。利用线性OKVS的性质，此处有

Decode （C，x）=Decode （B′，x）-ΔDecode （P，x）

Decode （C，x）=Decode （B′，x）-ΔH2（x）（5）

成立。因此，上述等式的左右两式即为该PSI协议的掩码。P1可计算X′：={Decode（C，x）|x∈X} ，P2可计算Y′={Decode（B′，y）-ΔH2（y）|y∈Y}。X′∩Y′即可计算出双方的交集。

3.4.2 TEE

令TEE支持以下3个安全算法，这些安全算法由TEE在安全内存中执行，保证其算法的正确性、隐私性。在TEE中定义两块隔离的安全内存M1、M2分别作为参与方P1与P2调用执行TEE算法时所执行使用的内存空间。即便是Pi也只能通过安全算法才能获取Mi中的临时计算数据。

1）TEEV（Pi：{（pkj，σj，mj）}，{m′j} ）：参与方Pi输入认证人公钥pkj，数字签名σj，参与方资质mj。在安全内存Mi中以（pk，m）的形式维护表Ti。若满足V（pkj，σj，mj）=1且mj∈{m′j}，则更新列表Ti：=Ti∪{（pkj，mj）}，否则说明Pi伪造了非法输入，PCI协议中断。

2）TEEQ （P1：X，C，r;P2：Y′）：P1输入认证人集合X，VOLE协议输出的C，随机值r∈{0，1}κ；P2输入集合Y′：={{0，1}κ}。初始化输出集合I={I1，Ii，2}，i∈{1，2}。对于每一个x∈X，算法判断H1（Decode （C，x，r））∈Y′，x∈T1，x∈T2是否均成立。若成立，则I1：=I1∪{x}，I1，2：=I1，2∪{m″}，I2，2：=I2，2∪{m′}，其中：m′为T1中x对应的资质；m″为T2中x对应的资质。TEE向P1输出{I1，I1，2}，向P2输出{I1，I2，2}。此外，若H1（Decode （C，x，r））∈Y′成立但xTi，可说明Pi伪造输入x，PCI协议中断。

3）TEEF（P1，P2）：参与方P1与P2要求TEE对安全内存M1，M2进行内存释放。

TEEQ与TEEF 必须由双方同时调用，TEEQ 用于在TEE中得到PCI协议的输出。同时，TEEV与TEEQ 还能检测参与方是否使用了恶意的输入。此外，TEEQ算法执行结束（即PCI协议结束）后，双方才会共同调用TEEF进行安全内存的释放，即TEEF必须两方同时释放。这避免了恶意参与方提前释放安全内存。

3.5 协议构造

参与方为P1与P2，它们的私有输入分别为p1，1={xj，σ1，j，m1，j}与p2，1={yj，σ2，j，m2，j}，公开输入分别为p1，2={m′2，j}与p2，2={m′2，j}。本文所提PCI协议的正式描述如协议1所示。

协议1：基于TEE的高效PCI协议

输入：P1：p1，1；P2：p2，1

输出：P1：{I1，I1，2}；P2：{I1，I2，2}

公共：P1：p1，2={m′2，j}；P2：p2，2={m′2，j}

//签名校验阶段

1： P1调用T1←TEEV （p1，1 ，p1，2 ），注意T1保存于安全内存M1，且Pi无法访问。

2： P2调用T2←TEEV （p2，1 ，p2，2 ），注意T2保存于安全内存M2，且Pi无法访问。

//计算掩码阶段

3： P1选择随机数r，r′←{0，1}κ，计算线性OKVS：P：=Encode （L，r），其中L=（xj，H2（xj，r′））。

4： P1与P2执行一个VOLE协议，P1得到向量A，C；P2得到向量B与标量Δ满足

C=ΔA+B。

5： P1发送A′：=P+A给P2，P2随后计算B′=B+ΔA′。

6： P2计算Y′={ H1（Decode （B′，yj ）-ΔH2（yj ））}。

//安全求交阶段

7： P1输入{xj}，C，r，P2输入Y′，共同调用{ I1，Ii，2} ←TEEQ （{ xj}，C，r;Y′），i∈{ 1，2＼}。

TEE将{I1，I1，2}发送给P1，将{I1，I2，2}发送给向P2。

8： P1与P2执行调用TEEF对安全内存M1，M2进行内存释放。

T1与T2是由TEEV 生成的2个临时列表，存储双方验签通过的认证人与资质集合。在最后的安全求交阶段，TEEQ 算法的本质是计算P1的掩码X′，然后计算X′∩Y′，并询问交集是否存在于Ti。若存在则说明该交集元素（认证人）与对应的资质是合法输出。这表明该交集元素既属于双方认证人的交集，同时该认证人所发布的签名证书在TEE中被验签通过。因此，我们在此处只需证明PSI协议是有效的即可，即X′∩Y′确是两方的认证人的交集。当x=y时，我们需证明掩码H1（Decode （C，x，r））与H1（Decode （B′，y）-ΔH2（y））相等，如下所示。

Decode （B′，y）-ΔH2（y）

=Decode （B+Δ（A+P），y）-ΔH2（y）

=Decode （C+ΔP，y）-ΔH2（y）

=Decode （C，y）+ΔDecode （P，y）-ΔH2（y）

=Decode （C，y）+ΔH2（y）-ΔH2（y）

=Decode （C，y）

=Decode （C，x）（6）

因此，所提PCI協议正确性成立。此外，由于TEE中可嵌入不同的签名验签算法，即便在同一个TEEV中，TEE也可执行不同的验签算法。

3.6 协议应用

在Web3.0中，当2个用户需要在无可信第三方CA下建立信任机制时，他们可以采取以下步骤：首先，双方公开生成证书的签名算法，并选择合适的第三方TEE机构，以便进行证书的验证服务和CA的求交。这一过程遵循PCI协议。在该过程中，用户双方需要将CA的公钥列表嵌入到TEE中，以便TEE提供证书验证服务，同时确保不在交集内的CA公钥不会泄露，因为TEE是可信的。最后TEE将求得的交集分别发送给2个用户。值得一提的是，类似蚂蚁的隐语等平台已经提供了类似的TEE服务。与GHOSH等［15］提出的PCI协议相比，本文所介绍的PCI协议更适用于Web3.0中的实际应用场景。

3.7 安全性分析

本文所提PCI协议是抗恶意敌手的。

首先，上述协议的验签过程是由TEE完成，且由于数字签名的公开验证性质，TEE能够对P1与P2的输入进行校验。同时，在验签过程中（第1、2步），P1与P2没有收到消息，因此视图为空。

协议1的第3步到第6步本质是一个抗恶意敌手的不经意伪随机函数（oblivious pseudorandom function， OPRF）协议，具体证明可查阅文献［20］。其中VOLE协议的具体证明可查阅文献［12］。

协议1的第7、8步由TEE完成，因此P1与P2在第7、8步从得到的视图中无法获取额外的信息。此外，第7、8步的正确性（在恶意敌手存在时能得到正确的输出）可查阅文献［13］。

4 实验与分析

本节实现所提PCI协议并对其进行性能测试，并与文献［15］的PCI协议进行对比。

4.1 实验环境以及参数

测试的硬件平台采用Intel i7-1165G7处理器、内存为16 GiB、主频为2.8 GiHz。操作系统为Ubuntu20.04，编程语言为C++。TEE本文采用蚂蚁集团提出的TEE框架［24］。根据文献［15］ PCI协议的设定，我们将输入大小设置为1 000。此外，由于本文所提PCI协议支持多种数字签名算法，我们分别使用ECDSA［17］、RSA［18］、SM2［19］这3种算法在128位安全等级下进行效率测试。

4.2 功能分析

文献［15］的PCI协议与本文所提PCI协议在功能方面的对比结果如表1所示。从表1可以看出，所提PCI协议不仅能够在保护非交集认证人隐私的前提下完成PCI协议，同时能在同一个协议中使用不同的数字签名算法。在本文的PCI协议中，验签算法是由TEE完成的。因此，仅需在TEE中事先实现各种验签算法，然后在执行验签过程时根据签名类别调用不同的验签算法即可。此外，由本文3.7节可知本文所提PCI协议也是抗恶意敌手的。

4.3 性能分析

从协议1中可以看出所提PCI协议需要的计算开销大约为N1+N2次数字签名的验签算法与1次PSI求交。在PCI协议中，我们仅统计一些较为耗时的计算操作，如表2所示。

从表2中可以看出，所提PCI协议的性能主要取决于3点：验签算法TEEV性能；VOLE协议效率；OKVS构造加解码效率。在所提PCI协议中，我们使用目前最优的VOLE协议［12］（仅需0.3 s即可生成百万量级的OKVS）与OKVS构造［13］（能够在0.2 s左右完成百万量级数据的加解码）。同时，验签算法TEEV不再需要耗时的基于秘密共享的MPC协议。因此，本文所提PCI协议在性能方面远远优于文献［15］的PCI协议。

4.4 实验效率

本节首先给出在使用不同的数字签名算法时，本文所提PCI协议的实际运行时间，如图5所示。

由图5可知：当使用ECDSA与SM2的验签算法时，本文所提PCI协议可在1.2 s左右完成输入大小为1 000的双方认证人集合求交。此外，当认证人使用RSA签名算法进行证书的验签时，协议的效率相比于使用ECDSA与SM2签名算法较慢（需要17 s）。这是因为本文所提PCI协议的大部分计算存在于证书的验签阶段。本文所使用的PSI协议是极度高效的，具体详情可查阅文献［13］。在相同安全等级下，RSA执行一次证书验签过程比ECDSA与SM2签名算法慢了很多。在我们的实验环境下，当安全等级为128位时，执行一次RSA、ECDSA、SM2的证书验签过程分别需要17.51 ms、0.49 ms、0.56 ms。因此，在本文提出的PCI协议中，我们推荐认证人使用ECDSA、SM2等基于椭圆曲线的数字签名算法。

此外，我们还将本文所提的PCI协议与文献［15］的PCI协议进行了效率方面的对比，如表3所示。在NDSS中，GHOSH等的PCI协议仅支持ECDSA的验签算法，出于对比实验的公平，在运行本文PCI协议时使用的也是ECDSA的验签算法。

从表3可以看出，本文所提PCI协议在效率上明显优于文献［15］的PCI协议。本文所提PCI协议的运行与输入大小呈线性关系，而文献［15］的PCI协议的运行时间会随着输入大小的增加快速地增加。因此，本文所提的PCI协议即便是认证人集合存在较大输入量时，仍能在稳定的时间内完成认证人求交，而文献［15］的PCI协议则无法实现该功能。此外，本文所提PCI协议比文献［15］的PCI协议效率更高的主要原因是本文所提PCI协议没有使用耗时更高的MPC框架进行验签。同时，由于本文所提的协议是基于现有的高性能PSI协议［13］构造而来，所以其进行隐私保护认证人求交过程异常高效。

5 结论

本文基于TEE和现有高效的抗恶意敌手PSI协议提出了一种新的PCI协议。该协议能够实现参与双方在去中心化CA场景下建立信任机制。本文提出的PCI协议能够在1 s左右完成输入大小为1 000的求交与验证，相较于GHOSH等的原始PCI协议具有较大的性能优势。此外，本文PCI協议能够支持不同的认证人使用不同的数字签名算法生成证书，更加符合实际需求。本文所提出的PCI协议显著地增强了Web3.0中用户数据的隐私性，具有较好的实际应用价值。

参考文献：

[1]杨雄. 云环境下融合FHE和人脸识别的身份认证方案［J］. 贵州大学学报（自然科学版）， 2019， 36（6）： 37-41.

［2］ 徐慧华， 杨雄， 张晓惠. 云计算环境下基于全同态加密的人脸信息保护［J］. 贵州大学学报（自然科学版）， 2021， 38（3）： 83-91.

［3］ TANG F， LING G W， CAI C C， et al. Solving small exponential ECDLP in EC-based additively homomorphic encryption and applications［J］. IEEE Transactions on Information Forensics and Security， 2023， 18： 3517-3530.

［4］ LI Z T， XIANG Y X， SHI J， et al. Make Web3.0 connected［J］. IEEE Transactions on Dependable and Secure Computing， 2021， 19（5）： 2965-2981.

［5］ TANG F， MA S， XIANG Y， et al. An efficient authentication scheme for blockchain-based electronic health records［J］. IEEE Access， 2019， 7： 41678-41689.

［6］ 唐飛， 包佳立， 黄永洪， 等. 基于属性的多授权中心身份认证方案［J］. 通信学报， 2021， 42（3）： 220-228.

［7］ DUA A， BARPANDA S S， KUMAR N， et al. Trustful： a decentralized public key infrastructure and identity management system［C］// 2020 IEEE Globecom Workshops GC Wkshps. Piscataway： IEEE， 2020： 1-6.

［8］ CHEN H， LAINE K， RINDAL P. Fast private set intersection from homomorphic encryption［C］// Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security. New York： ACM， 2017： 1243-1255.

［9］ GORDON S D， HAZAY C， LE P H. Fully Secure PSI via MPC-in-the-Head［C］// Privacy Enhancing Technologies. Cham： Springer， 2022： 291-313.

［10］PINKAS B， SCHNEIDER T， ZOHNER M. Faster private set intersection based on OT extension［C］// USENIX Security Symposium. Berkeley： USENIX， 2014： 797-812.

［11］KOLESNIKOV V， KUMARESAN R， ROSULEK M， et al. Efficient batched oblivious PRF with applications to private set intersection［C］// Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security. New York： ACM， 2016： 818-829.

［12］COUTEAU G， RINDAL P， RAGHURAMAN S. Silver： silent VOLE and oblivious transfer from hardness of decoding structured LDPC codes［C］.//Annual International Cryptology Conference. Cham： Springer， 2021： 502-534.

［13］RAGHURAMAN S， RINDAL P. Blazing fast PSI from improved OKVS and subfield VOLE［C］//ACM SIGSAC Conference on Computer and Communications Security. New York： ACM， 2022： 2505-2517.

［14］GHOSH B C， VINAYAGAMURTHY D， RAMAKRISHNA V， et al. Privacy-preserving negotiation of common trust anchors across blockchain networks［C］// 2022 IEEE International Conference on Blockchain and Cryptocurrency （ICBC）. Piscataway： IEEE， 2022： 1-5.

［15］GHOSH B C， PATRANABIS S， VINAYAGAMURTHY D， et al. Private certifier intersection［C］// The Network and Distributed System Security Symposium 2023. Rosten： ISOC， 2023： 1-18.

［16］DAI W Q， JIN H， ZOU D Q， et al. TEE： a virtual DRTM based execution environment for secure cloud-end computing［C］// ACM Conference on Computer and Communications Security. New York： ACM， 2010： 663-665.

［17］JOHNSON D， MENEZES A， VANSTONE S. The elliptic curve digital signature algorithm （ECDSA）［J］. International Journal of Information Security， 2001， 1： 36-63.

［18］RIVEST R L， SHAMIR A， ADLEMAN L. A method for obtaining digital signatures and public-key cryptosystems［J］. Communications of the ACM， 1978， 21（2）： 120-126.

［19］國家密码管理局. SM2 椭圆曲线公钥密码算法 第 1 部分： 总则： GM/T 0003.1—2012［S］. 北京： 中国标准出版社， 2012.

［20］RINDAL P， SCHOPPMANN P. VOLE-PSI： fast OPRF and Circuit-PSI from Vector-OLE［C］// Annual International Conference on the Theory and Applications of Cryptographic Techniques. Cham： Springer， 2021： 901-930.

［21］PINKAS B， ROSULEK M， TRIEU N， et al. PSI from PaXoS： fast， malicious private set intersection［C］// Annual International Conference on the Theory and Applications of Cryptographic Techniques. Cham： Springer， 2020： 739-767.

［22］PAGH R， RODLER F F. Cuckoo hashing［J］. Journal of Algorithms， 2004， 51（2）： 122-144.

［23］CANETTI R. Security and composition of multiparty cryptographic protocols［J］. Journal of Cryptology， 2000， 13： 143-202.

［24］SHEN Y， TIAN H， CHEN Y， et al. Occlum： secure and efficient multitasking inside a single enclave of intel SGX［C］// International Conference on Architectural Support for Programming Languages and Operating Systems. New York： ACM， 2020： 955-970.

Private Certifier Intersection Protocol Based on

Trusted Execution Environment

Abstract：

Ghosh et al. first introduced the Private Certifier Intersection （PCI） protocol at NDSS 2023， aiming to establish trust among users within a decentralized environment. In the PCI protocol， parties holding different certificates can compute a common set of certifiers， i.e.， Certificate Authorities （CA）， and verify the validity of these certificates while maintaining privacy.The PCI protocol can be used to solve the problem of establishing mutual trust mechanisms between two users in a decentralized environment without prior knowledge. Ghosh et al.s protocol utilizes a complex secure multi-party computation approach， leading to inefficiency. Additionally， it requires both participating parties to utilize the same signature algorithm， making it impractical. To address these issues， a new PCI protocol is introduced， which leverages a Trusted Execution Environment （TEE）. This novel protocol utilizes TEE to accomplish private certifier intersection， allowing both parties to use their preferred digital signature algorithms， thereby enhancing practicality. Experimental results show that the proposed protocol surpasses Ghosh et al.s PCI protocol in terms of efficiency.

Key words：

private certifier intersection; trusted execution environment; signature; decentralized