基于ARIMA构建SWECPX模型解决电商需求预测问题

向俊坤 郁佳幸 高贺 孙浩翔

摘 要：本文针对电商需求预测问题，基于促销节日因素S（Sale）和仓库因素C（Category），借助Matlab、Excel软件进行数据预处理，以ARIMA时间序列模型为核心，建立SWECPX（Sale Ware Effect Category Product X）模型，使用Matlab软件中的X-12-ARIMA选项等方法进行求解，实现了对商品需求量的准确预测，取得较好的1-wrmape指标测试效果。本文最大的创新点是提出了SWECPX模型，对影响商品需求量的要素S和C进行区分和求解，使对商品需求量预测更加精确，1-wrmape值较高。当每日的商品需求量处于较低水平时，预测效果的提升尤為显著，其预测值几乎与实际值相同。因此，我们期望SWECPX模型可以为电商仓储平台的决策提供切实的参考和借鉴。

关键词：ARIMA模型；SWECPX模型；时间序列；电商需求预测；电商平台

本文索引：向俊坤，郁佳幸，高贺，等.<变量 2>[J].中国商论，2024（08）：-032.

中图分类号：F742 文献标识码：A 文章编号：2096-0298（2024）04（b）--04

1 问题介绍

为了便于商品货物的统一调度，电商平台会提供配套仓库供电商储存货物。当今物联网技术发达，物流与数学理论、计算机技术结合紧密，通过大数据预测可以降低库存成本，并且为商家提供足够的存储能力。供应链优化问题的重点一般包含两个方面：需求预测和库存优化。本文数学建模主要解决需求预测问题。

在平常时期内，商店需求量维持在一个较低的、平稳的水平；在大卖时期内，商店的需求量会经历从较低的、平稳的水平突然上升到一个较高水平。商店的需求量不断经历从平常时期转进为大卖时期，又从大卖时期转进为平常时期，可以概括为商店的需求量具有在短期突变和长期趋变特性，不断经历从平稳的、较低的水平与较高的水平之间的相互转变。

根据互联网消费使用习惯和不同仓库的出货趋势，认为由平常时期进入大卖时期的主要原因在于仓库因素（C）和电商平台促销因素（S）。

2 模型假设

（1）假设没有仓库、网店倒闭，没有商品停产。

（2）仅考虑问题中的仓库、商品种类、商家因素，不考虑次要因素的影响。

3 模型框架

为了求解问题，本文建立SWECPX（Sale Ware Effect Category Product X）模型，其中S表示商家促销节日，W表示商品种类，E表示促销成效，C表示仓库，P表示商品，X表示对于新的影响维度该模型同样适用。

经过研究发现，商品P需求量走势主要受商品种类W与仓库C两者的影响，而直接影响不同商品种类需求量变化的原因是各大电商举办的促销节日S。电商针对特定种类商品的促销节日和对全部商品通用的促销节日S，促使各类商品P在不同时间进入大卖期。

本文通过SWCPX三级模型，结合ARIMA模型，可以使大卖时期的预测结果更加准确。

4 实验设置

ARIMA模型，属于时间序列分析中的一种[1]。ARIMA模型的优势在于可以处理非平稳的时间序列，商品的储存数量在时间序列上是非平稳的，其均值、方差随时间发生变化。ARIMA模型通过对数据进行差分处理，可以将非平稳时间序列转换为平稳时间序列，从而使模型可以对其进行有效建模。

式（1）中，p和q是模型的自回归阶数和移动平均阶数；φ和θ是不为零的待定系数；εt独立的误差项。

本文的实验主要在数学软件Matlab上进行，以ARIMA时间序列模型为核心，使用Matlab软件中的X-12-ARIMA选项[2]等方法对数据集进行求解与分析。在实验结果分析部分逐步给出最终的SWECPX模型。

5 实验结果分析

5.1 商品种类－商品模型（WP）的建立与分析（以服装商品为例）

5.1.1 时间序列上服装商品需求量平稳性的ADF检验[3]

本文通过Matlab对数据进行ADF检验（adftest），来对时间序列的平稳性做进一步判断。

经过ADF检验得出的函数返回值：

h=1，pValue=0.045，stat=-1.989，cValue=-1.9424

由于pValue接近0.05，并且stat与cValue相差较小，说明原假设被拒绝的概率较高，所以序列不平稳。

5.1.2 差分法对服装商品需求量的平稳化处理

由于相关数据具有长期趋变和短期突变性，且时间序列的趋势呈现非线性趋势，所以是一个变形时间序列，需要对序列进行平稳化处理。

使用差分法对相关数据进行平稳化处理。差分法公式：

式（2）中t代表时间，y代表随时间t变化的因变量，即商品的需求量。式（2）的含义是经过一次差分处理后的商品需求量折线图。

通过Matlab对数据进行ADF检验，得到数据：

h=1，pValue=0.001，stat=-10.1951，cValue=-1.9425

从函数返回值判断，数据平稳，与根据折线图得出判断相同，此时时间序列平稳。

5.1.3 模型定阶

通过对序列的自相关图和偏自相关图进行判别，可以对模型定阶，进而确定模型阶数的d、p、q。由于模型进行了1次差分，所以d=1。

拖尾是指偏自相关函数PACF按指数衰减或成正弦波形式，不能在某一步之后为零。截尾是指自相关函数ACF在一定阶数之后应为零，称其具有截尾性。

文章对差分后的数据，进行自适应性ACF和偏自相关性PACF分析[4]可得，自相关系数和偏自相关系数都拖尾，在1阶位置就开始基本落在2倍标准差范围，所以p=1，q=1，是ARMA（1，1）模型。

综合以上分析，确定应用d=1，p=1，q=1的ARIMA （1，1，1）模型。

5.1.4 对服装商品需求量趋势预测并检验

将服装商品总供应天数的前90%共151天划分为训练集，用训练集的数据投喂算法，对后10%共15天进行预测，然后对比预测结果和预测集实际值的差别，验证预测效果。

使用ARIMA（1，1，1）模型对服装商品总供应天数的训练集，共151天进行预测，用训练集的数据投喂算法，对后10%共15天进行预测。

本文用1-wrmape评价预测结果[5]，然后对比预测结果和预测集实际值的差别，验证预测效果。

式（3）中表示用训练集预测第i天需求量值，yi表示测试集第i天的实际需求量，wrmape越大，表示预测值与测试集中的数据差距越大，模型预测效果越差。1-wrmape越小，模型测试效果越差，1-wrmape越大，模型测试效果越好。

对服装商品的训练集预测结果进行1-wrmape评价，得到结果：wrmape=0.2089，1-wrmape=0.7911，接近0.8，模拟效果较好。

5.1.5 product-1426型商品与服装商品特性对比

为验证服装需求量作为整体，其特点是否具有一般性，从所有服装产品中选取一类产品进行趋势分析和预测，评价服装需求量的趋势是否对服装类产品具有适用性。本文选取product_1426，即1426型产品，对其需求量变化趋势与服装需求量变化趋势绘制堆叠折线图进行对比，对比结果如图1所示。

图1 product-1426型商品与服装商品特性折线对比堆叠图

两条折线趋势基本相同，1426型商品与服装整体需求量的大卖时期和平常时期吻合，说明服装商品特性模型对单种服装产品具有一般性。所以可以初步判定，对服装商品需求量的预测可以用于对某一件服装商品的需求量进行预测。

5.1.6 对product-1426型商品训练集预测与评价

本文对product-1426型商品的训练集预测结果进行1-wrmape评价，得到结果：wmape=0.2665，1-wrmape=0.7335，模拟效果较好，但比服装商品总体需求的1-wrmape值0.7911小，是因为product-1426型商品总数据数量较小，训练集数据也较小，训练效果不如服装类总商品以大量数据做支撑的预测效果。

从预测结果来看，同样选取样本的90%为训练集头尾数据，对后10%也就是后15天进行预测，经过1-wrmape评价，得到product-1426型商品的1-wrmape值为0.7335，服装商品的1-wrmape值为0.7911，两者预测效果较好，而product-1426型商品1-wrmape值較低的原因是测试集数据较少，所以预测效果不如服装整体的预测效果是正常的、可接受的。

根据以上数据，可以得出结论：商品种类在需求量趋势上与该类商品具有相似性，基于ADF检验、图检验、预测结果检验、逻辑验证，可以ARIMA时间序列模型为基础建立商品种类－商品模型。

5.2 促销节日－商品种类模型（SW）的建立与分析

从2022年12月1日到2023年5月10日，服装商品的需求量在总体上呈现上升趋势，即服装商品的长期趋变性是上升趋势。

根据Matlab软件已设定的X-12-ARIMA方法的自动选项，本文选择5月1日五一大促促销节日对服装类型商品的影响因素进行判别并且得到促销成效E服装商品5.1=3.5。

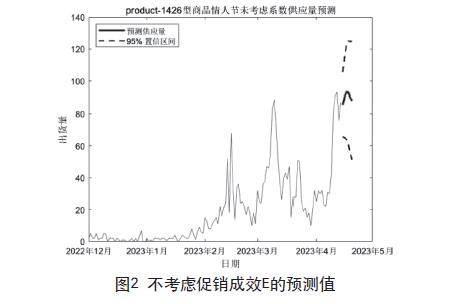
将服装商品2023年4月15日到2023年4月20日作为预测集进行预测，在不考虑促销成效E时，预测效果：

Wmape=0.5882，1-Wmape=0.4118。

将服装商品2023年4月15日到2023年4月20日作为预测集进行预测，在考虑促销成效E时，加入新的代码预测效果：

Wrmape=0.3042，1-wrmape值为0.6958。加入促销成效E后。

对比真实值：

从图像上，考虑促销成效E的预测值更贴合实际折线图；从1-wrmape评价上，考虑促销成效E的1-wrmape值为0.8454，不考虑促销成效E的1-wmape=0.4118。考虑促销成效E使预测结果的1-wrmape值提高了105%。

5.3 仓库－商品模型（CP）的建立与分析

与促销成效E的计算方法相同，根据Matlab软件已设定的X-12-ARIMA方法的自动选项，本文选择对仓库1的影响因素进行判别并且得到5月1日时间段内C1仓库5.1=2。

将服装商品2023年4月15日到2023年4月20日作为预测集进行预测，在考虑仓库因素C时，预测效果：

当考虑Wmape=0.2574仓库因素C时，1-Wmape=0.7426。不仓库因素C时wmape=0.5882，1-wmape=0.4118。当考虑仓库因素C时，1-Wmape评价值提高80.3%。

5.4 SWECP模型的数学表达

首先使用某商品的历史数据对ARIMA模型算法进行投喂，通过ADF检验得出t时刻的预测值Xt。

式（4）中，p和q是模型的自回归阶数和移动平均阶数；φ和θ是不为零的待定系数；εt独立的误差项。根据需要预测的时间段内的Xt形成一个从X1到Xt的时间序列，共t天。

由于E与C同时对商品的预测值产生影响，所以对E和C进行加权，并且需要判断商品是否进入大卖时期。

式（6）中A表示最终预测值，用α作为促销成效E的权重，用β作为仓库影响系数C的权重，其中α+β=1，即αE与βC同时对商品的预测值产生影响。α=1或0.8，β=1或0.2。

Et表示在t时间段内促销节日的促销成效，比如E2.14表示2月14日左右情人节期间电商的促销系数。Ct表示在t时间段内的仓库影响系数。

pte是促销节日判断系数，表示t时间段内商品是否受促销节日S的影响，若t时期内存在S，则pte=1，反之pte=0；ptc是仓库因素判断系数表示t时间段内商品是否受仓库C的影响，若t时期内存在C，则pte=1，反之pte=0。这里需要注意的是α和β也受pte和ptc的影响，因为若对于一件产品S和C只存在两者中的一个影响因素，其权重就会变为1，而不存在影响因素的权重变为0。

综上所述，SWECP模型的数学表达如下：

使用SWECP模型可以对各商家在各仓库的商品2023年5月16日至2023年5月30日的需求量、考虑新出现的商家+仓库+商品维度的需求量预测值、考虑6月规律性大型促销的预测值或者其他情况的预测值进行求解。

6 结语

6.1 模型的优点

（1）提出SWECPX（SaleWareEffectCategoryProductX）模型，对影响商品需求量的要素进行区分和求解。

（2）提出促销节日－商品种类－商品三级影响模型，就促销节日对产品需求量影响的内在规律做出归纳总结。

（3）提出促销成效E，促销节日对具体商品类型的促销成效E进行计算并制成表格方便查询。

（4）对于新的影响商品出货量维度X具有适应性，只要通过X-12-ARIMA模型对X因素的历史数值进行数据处理，就可以在考虑X因素的情况下精确预测数据。

（5）通过引入商品种类因素W和仓库因素C的预测值与不引入两因素的预测值对比，得出SWECPX模型预测更准确的结论。

6.2 模型的缺點

（1）对促销成效E的计算不够详细，没有对每一个导致商品进入大卖期的促销节日都进行计算。

（2）对仓库的出货量特点研究不够深入，没有细致讨论仓库出货量不同的特点和原因。

（3）数据预处理比较复杂。

6.3 模型的推广

针对电商需求预测问题，本文建立了SWECPX三级模型，可对各商家在各仓库的商品2023-05-16至2023-05-30的需求量、考虑新出现的商家+仓库+商品维度的需求量预测值、考虑6月规律性大型促销的预测值或者其他情况的预测值进行求解。该模型可以适用于任意新增加的X影响因素。本文的研究结果可以为电商仓储平台在价格促销时的决策提供切实的参考和借鉴。

参考文献

李玉翠，黄智铭，韦金玲.基于ARIMA模型的中越跨境电商发展趋势分析[J].对外经贸，2023（7）：6-10.

中国人民银行调查统计司.时间序列X-12-ARIMA季节调整：原理与方法[M].北京： 中国金融出版社，2006.

Paulus M P ， Kadtke J B， Menkello F V .STATISTICAL MECHANICS OF BIOLOGICAL AND OTHER COMPLEX EXPERIMENTAL TIME SERIES： ASSESSING GEOMETRICAL AND DYNAMICAL PROPERTIES[J].International Journal of Bifurcation & Chaos， 1993， 3（3）：717-727.

郑永龙，单奕萌，胡晨.基于ARIMA模型的MOSFET寿命预测方法[P].中国，CN202211237652.8[2023-11-22].

刘文星.网络攻击频率混沌时间序列预测[D].长沙： 国防科学技术大学，2009.