MATLAB在信源编译码技术教学中的应用研究

收稿日期：2023-11-28

基金项目：广西高等教育本科教学改革工程项目（2018JGB280）

DOI：10.19850/j.cnki.2096-4706.2024.04.040

摘  要：针对“通信原理”课程的重要教学内容——信源编译码技术具有概念抽象、理论性强、应用方法灵活等特点，以培养应用型人才为出发点，对该课程的教学改革进行了研究，引入MATLAB软件对重要的教学内容进行建模仿真和性能分析，在信源编译码技术教学中应用MATLAB软件演示了两种主要的信源编译码方法——脉冲编码调制和增量调制的程序和波形，提高了教学直观性及趣味性，促进了学生对信源编译码的基本方法和主要特点的理解和掌握，取得了较好的教学效果。

关键词：教学改革；信源编译码；应用型人才培养

中图分类号：TP391；G642      文献标识码：A  文章编号：2096-4706（2024）04-0195-04

Research on Application of MATLAB to Information Source Encoding and Decoding Technology Teaching

YANG Xiaofeng

（School of Physics and Telecommunication Engineering， Yulin Normal University， Yulin  537000， China）

Abstract： The content of information source encoding and decoding schemes in Communications Theory course is abstract and complicated. To keep pace with the trends of application-oriented talents cultivation， the author conducted teaching reform in Communications Theory course and applied MATLAB simulation to important teaching contents. When teaching information source encoding and decoding schemes， the author performed MATLAB simulation demo of two primary information source encoding and decoding schemes， that is， Pulse Code Modulation and Delta Modulation， which improve teaching intuitiveness and teaching quality a lot.

Keywords： teaching reform; information source encoding and decoding; application-oriented talents cultivation

0  引  言

“通信原理”是通信工程、电子信息工程等信息类专业重要的一门专业课程，是后续学习“计算机通信网络”“移动通信”等专业课程的基础，也是信息类专业考研的必考专业科目[1-3]。该课程主要讲授通信系统的基本原理、分析方法和设计方法，信源编译码技术是该课程的重点教学内容，主要讲授在数字通信系统发送端将模拟信源转化为数字信号、在接收端将接收到的数字信号还原回模拟信号的原理和方法，具有概念抽象、理论性强、应用方法灵活等特点。对于应用型本科高校信息类专业的学生来说，由于数学基础比较薄弱，理解和掌握这部分内容比较困难。

根据应用型本科高校的人才培养目标和因材施教的基本原则，笔者在进行信源编译码技术的教学时进行了如下教学改革：重点讲解基本理论的物理意义和应用方法，淡化公式的数学推导，引入MATLAB软件对重要的理论内容进行建模仿真和性能分析。利用MATLAB 软件强大的数值分析、信号处理和图形显示的功能，将其与信源编译码技术的教学相结合，可以提高教学直观性及趣味性，使学生从繁重的数学运算与推导中解脱出来，增强学生对理论知识的理解程度和应用能力[4，5]。

1  PCM编译码的教学

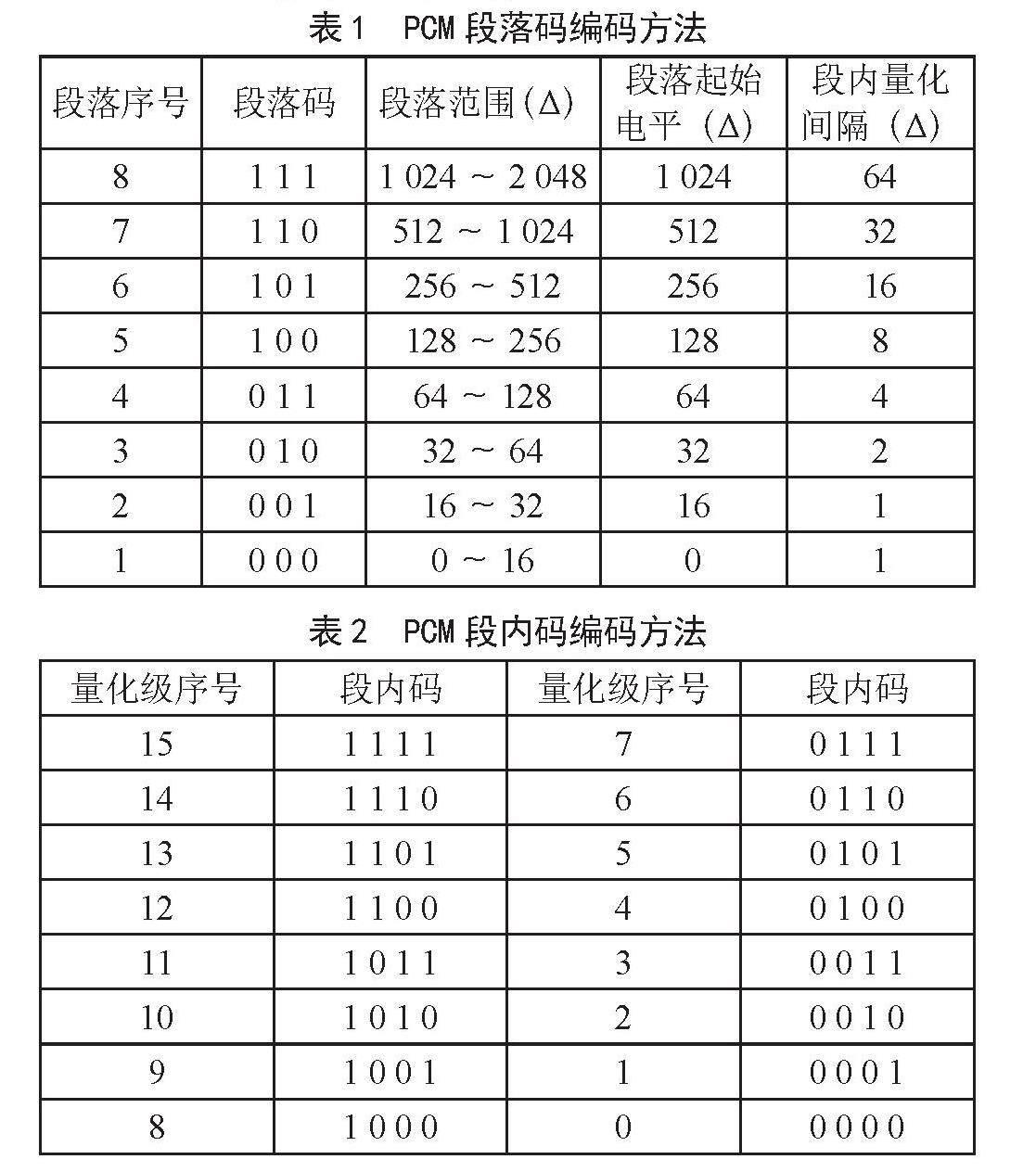
脉冲编码调制（Pulse Code Modulation， PCM）是最常用的一种信源编码方法[6-8]。教学重点为A律13折线PCM编码。首先介绍其基本原理：将输入信号抽样值归一化到[-1，+1]之间，将正、负区间各划分为不均匀的8段，每段均匀划分为16个量化间隔，一共2×8×16 = 256 = 28个量化间隔，可编为8位二进制码。然后介绍该8位码的编码方法：最高位为表示信号极性的1位极性码，正极性信号的极性码编为1，负极性信号的极性码编为0；极性码后面3位是表示信号所在段落的段落码；最低4位为表示信号所在该段落内量化间隔的段内码。段落码和段内码的编码方法如表1和表2所示。以最小量化间隔Δ=1/2 048为量化单位，各段起始电平和各段内量化间隔长度如表1所示。教学难点为如何确定信号所在段落和该段落内量化间隔的序号。重点介绍该问题的解决方法：将归一化的输入信号抽样值和各段起始电平进行比较，最接近且不大于输入信号抽样值的段落起始电平对应的段落即为信号所在段落；输入信号抽样值减去所在段落起始电平再除以该段内量化间隔长度的商即为所在该段落内量化间隔的序号。PCM編码的MATLAB实现子程序如下：

function [out]=pcm_encode（xq）

% xq为量化信号即PCM编码输入

n=length（xq）;

for i=1：n

% PCM极性码编码：

if xq（i）>0

out（i，1）=1;

else

out（i，1）=0;

end

% PCM段落码编码：

if abs（xq（i））>=0 & abs（xq（i））<16

out（i，2）=0;out（i，3）=0;out（i，4）=0;step=1;st=0;

elseif 16<=abs（xq（i）） & abs（xq（i））<32

out（i，2）=0;out（i，3）=0;out（i，4）=1;step=1;st=16;

elseif 32<=abs（xq（i）） & abs（xq（i））<64

out（i，2）=0;out（i，3）=1;out（i，4）=0;step=2;st=32;

elseif 64<=abs（xq（i）） & abs（xq（i）） <128

out（i，2）=0;out（i，3）=1;out（i，4）=1;step=4;st=64;

elseif 128<=abs（xq（i）） & abs（xq（i））<256

out（i，2）=1;out（i，3）=0;out（i，4）=0;step=8;st=128;

elseif 256<=abs（xq（i）） & abs（xq（i））<512

out（i，2）=1;out（i，3）=0;out（i，4）=1;step=16;st=256;

elseif 512<=abs（xq（i）） & abs（xq（i））<1024

out（i，2）=1;out（i，3）=1;out（i，4）=0;step=32;st=512;

elseif 1024<=abs（xq（i）） & abs（xq（i））<2048

out（i，2）=1;out（i，3）=1;out（i，4）=1;step=64;st=1024;

else

out（i，2）=1;out（i，3）=1;out（i，4）=1;step=64;st=1024;

end

% PCM段內码编码：

tmp=floor（（abs（xq（i））-st）/step）;

t=dec2bin（tmp，4） - 48;

out（i，5：8）=t（1：4）;

end

% PCM编码输出：

out=reshape（out'，1，8*n）;

表1  PCM段落码编码方法

段落序号 段落码 段落范围（Δ） 段落起始

电平（Δ） 段内量化

间隔（Δ）

8 1 1 1 1 024～2 048 1 024 64

7 1 1 0 512～1 024 512 32

6 1 0 1 256～512 256 16

5 1 0 0 128～256 128 8

4 0 1 1 64～128 64 4

3 0 1 0 32～64 32 2

2 0 0 1 16～32 16 1

1 0 0 0 0～16 0 1

表2  PCM段内码编码方法

量化级序号 段内码 量化级序号 段内码

15 1 1 1 1 7 0 1 1 1

14 1 1 1 0 6 0 1 1 0

13 1 1 0 1 5 0 1 0 1

12 1 1 0 0 4 0 1 0 0

11 1 0 1 1 3 0 0 1 1

10 1 0 1 0 2 0 0 1 0

9 1 0 0 1 1 0 0 0 1

8 1 0 0 0 0 0 0 0 0

PCM译码方法为：将极性码译为信号极性；根据表1将段落码译为信号所在段落，根据表2将段内码译为信号所在该段落内量化间隔的序号，然后根据表3用信号所在段落的起始电平加上该段落内量化间隔长度乘以所在量化间隔的序号再加上所在该段落内半个量化间隔的长度计算出信号的译码电平。PCM译码的MATLAB实现子程序如下：

function [out]= pcm_decode（y，v）

% y为输入信号的PCM编码，v为量化区间长度

n=length（y）;

y=reshape（y'，8，n/8）';

%各段落起始电平：

sg（1）=0;sg（2）=16;sg（3）=32;sg（4）=64;sg（5）=128;sg（6）=256;sg（7）=512;sg（8）=1024;

%各段落内量化间隔长度：

step（1）=1;step（2）=1;step（3）=2;step（4）=4;step（5）=8;step（6）=16;step（7）=32;step（8）=64;

for i=1：n/8

%极性码译码：

ss=2*y（i，1）-1;

%段落码译码：

sn=y（i，2）*4+y（i，3）*2+y（i，4）+1;

st=sg（sn）;

%段内码译码：

sl=（y（i，5）*8+y（i，6）*4+y（i，7）*2+y（i，8））*step（sn）+0.5*step（sn）;

% PCM译码输出：

out（i）=ss*（st+sl）/4096*v;

end

下面以输入信号x=sin（100πt）+0.5sin（300πt）为例说明如何运用MATLAB对该信号进行PCM编译码。MATLAB实现主程序如下，作图如图1所示。

clear all

close all

ts=0.001;                         %采样时间间隔

t=0：ts：20*ts;                    %仿真时间序列

x=sin（100*pi*t）+0.5*sin（300*pi*t）;

%输入信号

v=max（x）-min（x）;           %量化区间长度

xn=x/v;                           %输入信号归一化

xq=floor（xn*4096）;        %量化信號

y=pcm_encode（xq）;        % PCM编码

xd=pcm_decode（y，v）;     % PCM译码

%作图：

subplot（311）

plot（t，x）;ylim（[-1.5 1.5]）;title（'输入信号'）;

subplot（312）

stairs（y）;ylim（[-1.5 1.5]）;title（'PCM编码输出'）;

subplot（313）

plot（t，xd）;ylim（[-1.5 1.5]）;title（'PCM译码输出'）;

图1  PCM编译码

从图1可以看出，PCM译码波形和原输入信号波形比较相似，验证了PCM编译码的有效性，但是由于一个信号抽样值编为8位PCM码，需要较大传输带宽和传输速率。在教学中利用MATLAB仿真软件演示PCM编译码的程序和波形，可以帮助学生深入理解PCM编译码的方法和特点。

2  DM编译码的教学

增量调制（Delta modulation， DM）是PCM的一种改进方法[6-8]。在相同的信噪比条件下，DM比PCM具有更少的编码位数、更小的传输带宽和传输速率。首先介绍其基本原理：PCM是对每个信号样值独立编码，因为信号样值的取值范围较大，所以PCM需要较多的编码位数、较大的传输带宽和传输速率。而DM利用相邻信号样值的相关性减少信息冗余即对相邻信号样值的差值进行编码，因为相邻信号样值的差值取值范围较小，所以DM需要较少的编码位数、较小的传输带宽和传输速率。重点介绍DM编码方法：如果相邻信号样值的差值为正，则编为1；如果相邻信号样值的差值为负，则编为0。然后介绍DM译码方法：对应1码的译码电平上升一个量化台阶，对应0码的译码电平下降一个量化台阶，得到阶梯形的译码输出，再经过平滑滤波器得到平滑的译码输出。

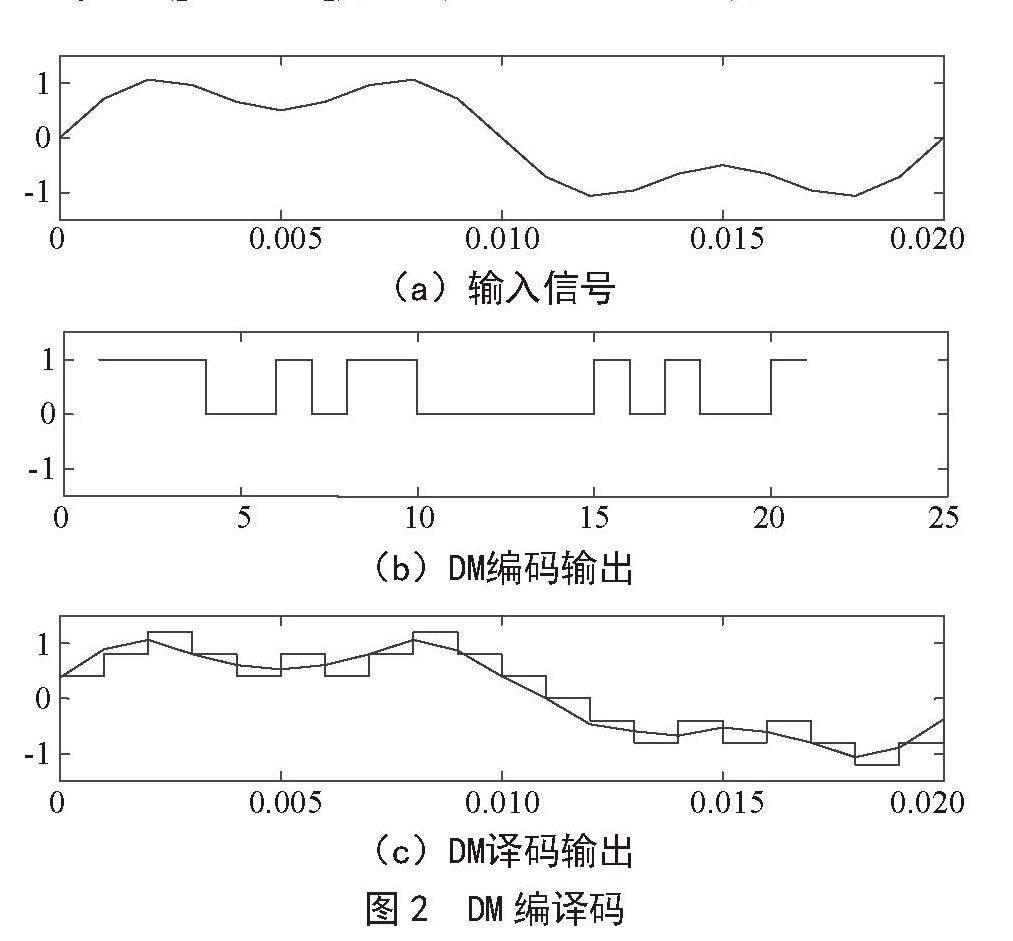
下面以与PCM编译码案例相同的输入信号x=sin（100πt）+0.5sin（300πt）为例说明如何运用MATLAB对该信号进行DM编译码。MATLAB实现程序如下，作图如图2所示。从图2可以看出，DM译码波形和原输入信号波形比较相似，验证了DM编译码的有效性。

clear all

close all

ts=0.001;                          %采样时间间隔

t=0：ts：20*ts;                     %仿真时间序列

x=sin（2*pi*50*t）+0.5*sin（2*pi*150*t）;

%输入信号

% DM编码：

delta=0.4;                         %量化台阶

ql1（1+length（t））=0;          %编码量化电平初始化

for k=1：length（t）

e（k）=x（k）-ql1（k）;          %量化误差

eq1（k）=delta*（2*（e（k）>=0）-1）;

%编码量化电平增量

ql1（k+1）=eq1（k）+ql1（k）;

%编码量化电平更新

y（k）=（eq1（k）>0）;          % DM编码输出

end

% DM译码：

ql2（1+length（t））=0;

%译码量化电平初始化

for k=1：length（t）

eq2（k）=delta*（2*y（k）-1）;

%译码量化电平增量

xd（k）=eq2（k）+ql2（k）;         %譯码输出

ql2（k+1）=xd（k）;                 %译码量化电平更新

end

%作图：

subplot（311）

plot（t，x）;ylim（[-1.5 1.5]）;title（'输入信号'）;

subplot（312）

stairs（y）;ylim（[-1.5 1.5]）;title（'DM编码输出'）;

subplot（313）

stairs（t，xd）;hold on;

plot（t，smooth（xd，'sgolay'））;hold off;

ylim（[-1.5 1.5]）;title（'DM译码输出'）;

图2  DM编译码

最后，引导学生对比PCM和DM编译码输出的波形图，总结这两种信源编译码方法的不同特点：对于同样的21个采样值的输入信号，PCM编码输出168位码，DM编码输出21位码，DM所需的传输带宽和传输速率更小、传输有效性更高；而PCM译码输出比DM译码输出更接近原输入信号的波形，因为信源编译码方法的抗量化噪声性能随编码位数的增加指数级增长，PCM编码位数为8位，DM编码位数为1位，因此PCM比DM具有更高的抗量化噪声性能、译码准确性更高。另外，DM量化台阶的取值同时影响量化噪声和过载噪声，量化台阶越大，则量化噪声越大，而过载噪声越小，所以应根据量化噪声和过载噪声折中选取合适的量化台阶[9，10]。

以上详细介绍了利用MATLAB实现PCM和DM两种信源编译码方法，两者的波形图直观地展示了各自不同特点，给学生留下深刻的印象。

3  结  论

笔者根据通信技术的发展趋势和因材施教的基本原则合理取舍教学内容，将MATLAB仿真引入“通信原理”课程教学中，利用MATLAB演示信源编译码方法PCM和DM的程序和波形，将重难点知识形象化，加强了课程内容之间的相互联系，能够充分调动学生的学习积极性与主动性，促进了学生对信源编译码的基本方法和主要特点的理解和掌握。通过上述教学改革，本课程的教学内容更加合理，教学方法更加科学，教学效果更加优良。

参考文献：

[1] 王玲玲，尹爱兵.应用型本科高校通信原理课程教学方法改革 [J].现代信息科技，2023，7（20）：173-176.

[2] 谢玉鹏.智慧三色“学导思辩研”的通信原理教学探索 [J].计算机教育，2023（10）：174-178+184.

[3] 宋俊慷，杨秀增，樊东红，等.一流本科专业建设背景下工程教育混合式教学改革探索——以现代通信原理课程为例 [J].大学教育，2023（12）：82-84.

[4] 杨小凤.MATLAB在数字滤波器教学中的应用 [J].教育教学论坛，2018（18）：207-209.

[5] 张谢馥，李健，于国龙.基于MATLAB的通信原理课程教学研究与实践 [J].创新创业理论研究与实践，2023，6（15）：168-170.

[6] 樊昌信，曹丽娜. 通信原理：第7版 [M].北京：国防工业出版社，2021.

[7] 曹丽娜，樊昌信. 通信原理：第7版 学习辅导与考研指导 [M].北京：国防工业出版社，2021.

[8] 郭文彬，杨鸿文，桑林，等.通信原理 基于Matlab的计算机仿真：第2版 [M].北京：北京邮电大学出版社，2021.

[9] 许书凯.蓝牙音频信号处理算法研究 [D].西安：西安电子科技大学，2020.

[10] 王欣，陶杰，康朝红.基于MATLAB/Simulink的DM和ADM编解码系统实验仿真 [J].通信技术，2020，53（10）：2588-2595.

作者简介：杨小凤（1984—），女，汉族，广西玉林人，副教授，硕士，主要研究方向：智能算法设计及应用。