基于SSA-LSTM模型的空气质量预测研究

曹还君 李长云

收稿日期：2023-11-08

DOI：10.19850/j.cnki.2096-4706.2024.04.030

摘  要：为提高PM2.5浓度的预测精度，提出了一种结合麻雀搜索算法（SSA）和长短期记忆神经网络（LSTM）的组合预测模型。以2023年5月至8月期间长沙市PM2.5浓度数据为基础，构建了SSA-LSTM模型并与其他模型进行了对比实验。实验结果显示，SSA-LSTM模型的预测结果在拟合优度（R2）上相较于单一LSTM、PSO-LSTM和WOA-LSTM模型分别提升了45.93%、31.55%、19.12%，同样在均方根误差（RMSE）和平均绝对误差（MAE）的结果上也表现更优，表明该模型在PM2.5浓度预测方面具有高准确性和有效性，可为制定PM2.5相关预防措施提供一定的参考价值。

关键词：麻雀搜索算法；长短期记忆神经网络；空气质量；PM2.5浓度预测

中图分类号：TP18    文献标识码：A  文章编号：2096-4706（2024）04-0142-06

Research on Air Quality Prediction Based on SSA-LSTM Model

CAO Huanjun， LI Changyun

（College of Computer Science， Hunan University of Technology， Zhuzhou  412007， China）

Abstract： To improve the accuracy of PM2.5 concentration prediction， a combined prediction model integrating Sparrow Search Algorithm （SSA） and Long Short-Term Memory （LSTM） neural networks is proposed. The SSA-LSTM model is developed based on PM2.5 concentration data from Changsha city， spanning from May to August in 2023， and is compared with other models. The results show that the SSA-LSTM model significantly outperformed the standalone LSTM， PSO-LSTM， and WOA-LSTM models in terms of fit quality （R2）， registering improvements of 45.93%， 31.55%， and 19.12%， respectively. Similarly， it also shows superior performance in terms of Root Mean Square Error （RMSE） and Mean Absolute Error （MAE）. These findings demonstrate the model has high accuracy and effectiveness in PM2.5 concentration prediction， providing a certain reference value for making the PM2.5-related preventive measures.

Keywords： SSA; LSTM; air quality; PM2.5 concentration prediction

0  引  言

進入21世纪以来，随着人类社会经济的快速发展，能源消耗量的剧增导致了环境污染问题的加剧，尤其是空气污染问题变得尤为严重。研究显示，长期暴露于高浓度污染物的环境中，不仅对人类健康构成直接威胁，也会给企业生产带来直接或间接的影响[1]。空气污染程度的主要指标是空气中的污染物浓度，其中PM2.5是影响空气质量的关键指标。由于体积小、重量轻，PM2.5能在空气中长时间滞留，并在吸入人体后对健康造成严重危害[2]，因此研究建立一个高效且精确的PM2.5浓度预测模型，有助于人们制定并采取必要的预防措施，具有重要的现实意义。

在PM2.5浓度预测的研究领域，国内外学者们已经探索了多种方法以提升预测的精度和实用性。早期的研究，学者们主要基于传统的统计学方法建立线性模型对PM2.5浓度进行预测，如多元线性回归模型（MLP）[3]、差分整合移动平均自回归模型（ARIMA）[4，5]

等。但由于影响PM2.5浓度的因素过多且相互之间关联性强，使得PM2.5浓度的变化具有毛刺多、陡升陡降的特点，导致传统的线性模型在预测这类具有非线性特征的复杂时间序列数据方面，预测误差较大，存在一定的局限性。近年来，随着人工智能技术的快速进步，机器学习方法得到了广泛应用，包括应用在了对PM2.5浓度预测的研究中，有效地克服了传统统计模型在预测复杂非线性时间序列数据方面的不足，取得了显著成果。其中随机森林[6]、支持向量机[7]、神经网络[8]等机器学习算法能够捕捉数据中的复杂模式和关系，已被证明在提高预测精度方面具有显著优势。特别是，长短期记忆神经网络[9]（Long Short-Term Memory， LSTM）模型作为循环神经网络（Recurrent Neural Network， RNN）的改进版本，通过其独特的门控机制解决了长序列数据在训练过程中的梯度消失和梯度爆炸问题，能够有效地捕捉和利用长期依赖关系，因而在处理非线性时间序列分析中发挥了重要作用。例如：潘永东等[10]利用LSTM模型对南京市的PM2.5浓度进行预测和趋势分析，取得了优于SVR、XGBoost和MLR模型的预测结果；肖敏志等[11]的研究也表明，LSTM模型在PM2.5浓度预测上的精度超过了RNN模型。然而LSTM模型的预测准确性高度依赖于其超参数的初始值设置，如迭代次数、学习率以及隐含层神经元数量等，而人工设置这些超参数往往存在诸多挑战[12]，可能导致模型构建困难和预测精度不足等问题，从而影响最终预测结果。

为解决上述问题并进一步提升预测精度，本文提出麻雀搜索算法[13]长短期记忆神经网络（Sparrow Search Algorithm-Long Short-Term Memory， SSA-LSTM）模型预测PM2.5浓度。研究基于长沙市2023年5月到8月期间的空气污染物浓度和气象数据，应用SSA对LSTM模型的超参数进行优化，构建了SSA-LSTM模型，并将其与单一LSTM预测模型、粒子群优化算法（Particle Swarm Optimization， PSO）优化的LSTM模型，以及鲸鱼优化算法（Whale Optimization Algorithm， WOA）优化的LSTM模型的预测结果进行对比分析。

1  基础理论

1.1  长短期记忆神经网络

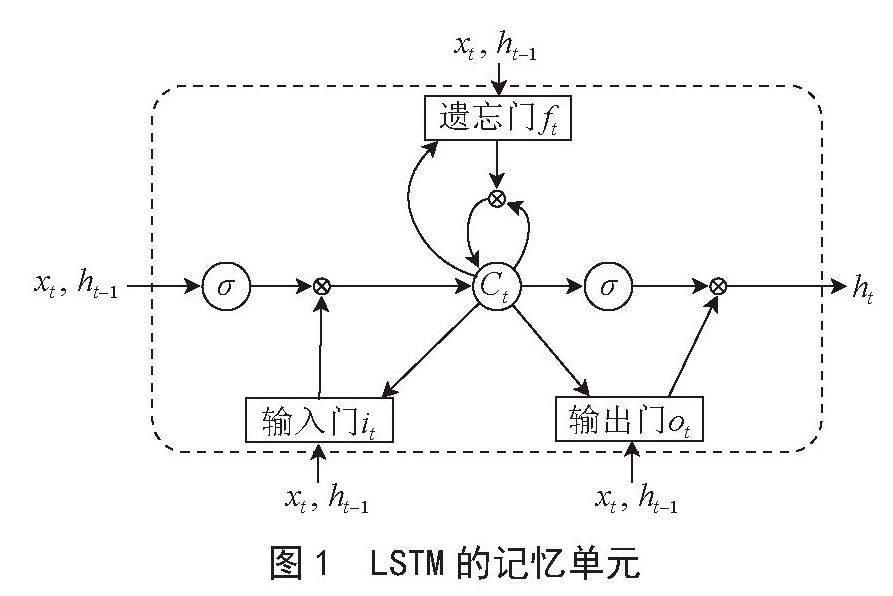
长短期记忆神经网络[9]（LSTM）是深度学习领域中一种重要的递归神经网络（RNN）变体，于1997年由Hochreiter和Schmidhuber首次提出，解决了传统RNN模型在长序列训练过程中的梯度消失和梯度爆炸问题，对于长时间序列数据的预测具有非常好的表现能力，LSTM的记忆单元如图1所示。

图1  LSTM的记忆单元

长短期记忆网络（LSTM）的核心在于其独特的细胞状态（Cell State），这一状态构成了网络的记忆核心，相当于一个内存單元，专门设计用于存储和传递时间序列信息。这一机制赋予了LSTM处理长期时间依赖性的能力，从而在处理序列数据时，能够维持关键信息的长期记忆。LSTM的记忆单元由三个主要的门控组件构成：输入门（it）、输出门（ft）和遗忘门（ot）。在时刻t，记忆单元接收输入向量xt，并更新其隐藏状态ht。门控结构的作用是调节信息流，其中输入门负责调控新信息的接入，遗忘门控制信息的保留与丢弃，而输出门则控制从记忆单元到输出的信息流。这些门的活动状态是通过学习得到的，初始状态分别设定为it、ft和ot，以便网络能够在训练过程中自适应地调整信息流的动态传递。

在LSTM中，存储单元的状态更新过程如下。

以下等式是输入门的数学表达式，它决定了哪些信息必须转移到单元中：

（1）

以下等式是遗忘门的数学表达式，它决定了要忽略哪些信息：

（2）

（3）

根据遗忘门和输入门的状态，来更新单元状态Ct，表达式为：

（4）

输出门负责更新输出，由以下等式给出，输出门还负责更新前一个时间步的隐藏层。输出门的最终输出为：

（5）

（6）

式（1）～（6）中，σ表示Sigmoid函数，会根据输入产生[0，1]之间的向量； 表示的是候选细胞信息；Wf 、Wi、Wo、Wc表示的是LSTM细胞状态更新过程中的权重系数矩阵；bf 、bi、bo、bc表示状态更新过程中的偏置矩阵。

1.2  麻雀搜索算法

麻雀搜索算法[13]（Sparrow Search Algorithm， SSA）源自对麻雀群体在自然界中觅食及逃避天敌行为的深入观察，是一种模拟生物群体智能行为的优化算法。该算法精确地抽象了麻雀在其生态系统中的行为策略和社会结构，明确划分为发现者、加入者以及警戒者三种角色。在此算法下，发现者承担着探索资源并指引群体觅食方向的重任，而加入者则依赖发现者的引导以获得资源，警戒者则在感知到威胁时向同伴发出警报，并引导群体采取避险措施。麻雀搜索算法具有求解精度高、收敛速度快、鲁棒性好的特点，在求解复杂优化问题时展现出了显著优势，尤其是在收敛速度和增强全局搜索能力方面表现出色，已成为解决各类优化问题的一种高效算法。

在麻雀搜索算法中，N只麻雀所组成的随机初始化种群表示如下：

（7）

式（7）中，d表示待优化问题变量的维数。麻雀种群的适应度表示如下：

（8）

式（8）中，f表示单只麻雀的适应度值。发现者的位置更新公式：

（9）

式（9）中，t表示当前的迭代索引且 ，其中itermax表示预定的最大迭代次数；j为维度索引， 表示第t次迭代中第i只麻雀的第j维的位置信息；参数α表示一个定义在区间（0，1]上的随机变量；ST和R2分别表示安全阈值和报警阈值；Q表示一个服从正态分布的随机变量；L表示一个全由1构成的1×d维矩阵。

当R2＜ST时，表示此时具有安全的觅食环境，发现者可进行大范围的搜索；当R2≥ST，表示当前觅食环境出现危险信息，整个麻雀种群需转移到安全区域进行搜索。加入者的位置更新公式：

（10）

式（10）中，Xp表示目前发现者所占据的最优位置；Xworst则表示当前全局最差的位置；A表示一个元素随机为1或-1的1×d维矩阵，并且A+ = AT （AAT）-1。

当i＞n / 2时，表明适应度较低的第i个加入者因无法获取食物而处于饥饿状态，需前往其他地方进行觅食从而补充能量。预警者的位置更新公式：

（11）

式（11）中，Xbest表示当前迭代中全体个体的最优位置；参数β和α都表示步长控制因子，其中β表示一个服从均值为0的且方差为1的正态分布的随机变量，而α表示一个值位于[-1，1]的随机变量；fg和fw分别表示当前迭代中的全局最优适应度值和最差适应度值；fi则表示当前麻雀个体的适应度值；ε表示一个趋近于0的变量，用以确保分母不为0。

当个体适应度fi大于全局适应度fg时，这表明该麻雀处于潜在的危险区域，易受到捕食者的攻击；当fi = fg时，位于种群中间的麻雀感知到危险的迹象，它们会倾向于靠近其他个体，以减少自身被捕食的可能性。

1.3  SSA-LSTM模型

LSTM模型的性能和预测准确性在很大程度上受到其超参数配置的影响，这些超参数包括但不限于迭代次数、隐含层神经元数量以及学习率等。传统的超参数调整方法往往依赖于经验和试错，这种方法不仅耗时而且缺乏系统性，很难保证达到模型性能的最优化。因此本文采用了智能优化算法——麻雀搜索算法（SSA），对LSTM模型的超参数进行系统地优化。通过SSA算法的全局搜索能力，可以確保LSTM模型在多维超参数空间中有效地探索，并快速稳定地收敛到全局最优解，从而显著提升模型的性能和预测精度。

此模型的优化过程包含以下几个步骤：

1）首先对缺失数据采用拉格朗日插值法对数据进行填补。之后执行归一化处理，根据式（12），将所有数据缩放到[0，1]区间中以消除量纲影响。

（12）

式（12）中，X表示原始数据；Xmin和Xmax分别表示原始数据中的最小值和最大值；Xnew表示归一化处理之后的数据。完成这些步骤后，再将数据集划分为训练集和测试集。

2）利用参数如最大迭代次数、麻雀种群规模、寻优维度以及生产者比例来初始化麻雀种群。采用训练集上的均方误差作为适应度函数，对LSTM网络的关键超参数——迭代次数、隐含层神经元数量和学习率进行自动优化。

3）计算种群中每个麻雀个体的适应度，并按适应度值进行排序，以识别当前具有最优和最差适应度的个体。

4）根据式（9）～（11）更新发现者、跟随者和预警者的位置。在每次迭代中，保留适应度最高的个体，并更新全局最优适应度值。

5）判断是否满足算法的终止条件，如果满足，则保存算法所寻到的最优参数；如果不满足，则返回步骤3）继续迭代优化过程。

6）使用优化后的超参数重构LSTM模型，并输入测试集数据以获得预测值。最后，对预测结果进行反归一化处理，以得到最终的预测结果。

构建的系统模型整体结构如图2所示。

图2  SSA-LSTM流程图

2  实验与结果分析

2.1  实验平台

本实验基于Python语言，使用JupyterLab进行代码编写和结果展示。具体实验环境及相关版本号如表1所示。

表1  实验环境配置

项目 版本

操作系统 Ubuntu 22（x86）

CPU Intel（R）Xeon（R）CPU E3-1231 v3

GPU NVIDIA Quadra K1200

内存 32 GB

Python 3.8.17

TensorFlow-GPU 2.3.0

Numpy 1.24.3

Matplotlib 3.7.1

2.2  数据来源

本文采用的数据来自中国环境监测总站（www.cnemc.cn），选取了2023 年5月1日0点到2023年8月25日23点的长沙市空气质量小时数据，包括PM2.5、PM10、SO2、NO2、O3等空气污染物浓度和风速、温度、湿度等气象数据共3 000条记录，其中前80% 数据作为训练集，后20%数据作为测试集。空气污染物浓度单位为μg/m3、温度单位为℃、风速单位为m/s、湿度单位为%RH。受篇幅限制，部分数据如表2所示。

2.3  评价指标

为了全面评估预测模型的性能，本实验选用了均方根误差（Root Mean Square Error， RMSE）、平均绝对误差（Mean Absolute Error， MAE）和拟合优度R2（Goodness of Fit）作为评价指标，计算公式如下：

（13）

（14）

R2 = 1 -                （15）

式中，Yi表示第i个时间点实际观测到的PM2.5浓度值， 表示模型预测的PM2.5浓度值，N表示观测序列的总长度。理想情况下，RMSE和MAE的值越低，表明预测误差越小；R2的值越接近1，则说明模型的预测能力越强，拟合度越高。

2.4  结果分析

SSA会对LSTM网络的超参数寻优，包括迭代次数、学习率、第1和第2隐含层的神经元数量，并以训练集的均方差（RMSE）为适应度函数，适应度函数值越大，表明模型训练结果越准确。设置麻雀种群中个体数目为10，寻优维度为4，最大迭代次数为10，发现者和警戒者在麻雀种群中所占比例分别为20%和10%，安全阈值ST为0.8。设置学习率的范围为[0.001，0.01]，迭代次数寻优范围为[10，100]，第1和第2隐含层的神经元数量范围为[1，100]。

为了充分证实所提出的SSA-LSTM模型在预测精度和有效性方面的优势，本文设计了以下对比实验，涵盖了单一LSTM模型、PSO-LSTM模型和WOA-LSTM模型。通过这些对比实验，旨在展示SSA-LSTM模型在处理PM2.5浓度预测问题时的性能表现。预测结果的对比展示在图3中，其直观反映了不同模型间的预测能力差异。

如图3所示的实验结果显示，SSA-LSTM模型在预测精度方面相对于单一LSTM模型具有显著提升，并且与PSO-LSTM模型和WOA-LSTM模型相比，展现出更优的拟合能力。这一结果凸显了SSA-LSTM模型在整体预测性能上的优越性。为了进一步量化各模型的预测效果，本文采用了式（13）～（15）定义的评价指标RMSE、MAE和R2进行计算，并将结果汇总至表3。

表3  实验结果

预测模型 评价指标

RMSE MAE R2

LSTM 2.407 6 1.938 4 0.874 8

WOA-LSTM 2.139 2 1.634 4 0.901 1

PSO-LSTM 1.968 2 1.488 1 0.916 3

SSA-LSTM 1.745 2 1.293 9 0.932 3

由表3可知，SSA-LSTM的预测结果拟合效果表现最佳，相较于单一LSTM模型、WOA-LSTM模型以及PSO-LSTM模型，SSA-LSTM的均方根误差（RMSE）分别降低了27.51%、18.42%、11.33%，平均绝对误差（MAE）分别降低了33.25%、20.83%、13.05%，拟合优度（R2）分别提高了45.93%、31.55%、19.12%。这些结果进一步证明了SSA-LSTM模型在提高PM2.5浓度预测准确性方面具有显著优势。

3  结  论

本研究提出了一种结合麻雀搜索算法和长短期记忆神经网络的PM2.5浓度预测模型（SSA-LSTM），针对空气质量评估的关键问题进行了探究。通过构建的SSA-LSTM模型，本文有效地解决了LSTM模型超参数的初始化设置难题，实现了对PM2.5浓度的精确预测，为相关领域研究提供了新的思路。基于长沙市2023年5月至8月的空气污染物浓度和气象数据，建立对比实验，实验结果表明，SSA-LSTM模型的预测结果相比于单一LSTM模型以及其他先进的组合模型（如PSO-LSTM和WOA-LSTM），表现出了更优秀的预测精度。

未来的工作将聚焦于进一步提升预测模型的实时性和动态适应性，探索实时数据流环境下的模型快速更新机制，并结合更多种类的环境数据源，以及考虑更加复杂的外部影响因素，例如区域工业活动、交通流量和天气变化等。同时，也应关注模型的可解释性，以便更好地理解模型预测结果背后的驱动因素，为政策制定者提供更可靠的决策支持。

参考文献：

[1] 李卫兵，张凯霞.空气污染对企业生产率的影响——来自中国工业企业的证据 [J].管理世界，2019，35（10）：95-112+119.

[2] 杨新兴，冯丽华，尉鹏.大气颗粒物PM2.5及其危害 [J].前沿科学，2012，6（1）：22-31.

[3] DIMITRIOU K，KASSOMENOS P. A study on the reconstitution of daily PM10 and PM2.5 levels in Paris with a multivariate linear regression model [J].Atmospheric Environment，2014，98：648-654.

[4] 黃婷婷，朱家明，刘丹丹.芜湖市PM（2.5）的影响因素分析与预测 [J].山西师范大学学报：自然科学版，2017，31（2）：88-93.

[5] JIAN L，ZHAO Y，ZHU Y P，et al. An application of ARIMA model to predict submicron particle concentrations from meteorological factors at a busy roadside in Hangzhou，China [J].Science of the Total Environment，2012，426：336-345.

[6] HU X，BELLE J H，MENG X，et al. Estimating PM2.5 Concentrations in the Conterminous United States Using the Random Forest Approach [J].Environmental Science & Technology，2017：6936-6944.

[7] LAI X，LI H，PAN Y. A combined model based on feature selection and support vector machine for PM2.5 prediction [J].Journal of Intelligent & Fuzzy Systems，2021：10099-10113.

[8] CHEN Y. Prediction algorithm of PM2.5 mass concentration based on adaptive BP neural network [J].Computing，2018：825-838.

[9] HOCHREITER S，SCHMIDHUBER J. Long short-term memory [J].Neural computation，1997，9（8）：1735-1780.

[10] 潘永东，曹骝，刘明.基于LSTM网络的PM2.5浓度预测 [J].金陵科技学院学报，2021，37（4）：7-13.

[11] 肖敏志，王淑君，宋巍巍.基于LSTM的PM（2.5）预测模型综述 [C]//2019中国环境科学学会科学技术年会论文集（第一卷）.西安：[出版者不详]，2019：949-952.

[12] GILIK A，OGRENCI A S，OZMEN A. Air quality prediction using CNN+LSTM-based hybrid deep learning architecture [J].Environmental Science and Pollution Research，2022：11920-11938.

[13] 薛建凯.一种新型的群智能优化技术的研究与应用 [D].上海：东华大学，2020.

作者简介：曹还君（2000—），男，汉族，湖南常德人，硕士在读，研究方向：工业大数据、智能信息处理；李长云（1971—），男，汉族，湖南衡阳人，教授，博士，研究方向：软件理论、物联网工程、人工智能。