拼图研究整式的乘法

赵维坤

小学里，我们学习了长方形、平行四边形、三角形面积等图形的面积计算，发现图形的面积可以用一个表达式表示。下面，我们利用面积的表达式进行新的研究。

请制作若干张3种类型的纸片：边长为a的正方形、边长为b的正方形和长为a、宽为b的长方形（如图1）。下面，我们利用这些纸片拼图，探究整式的乘法。

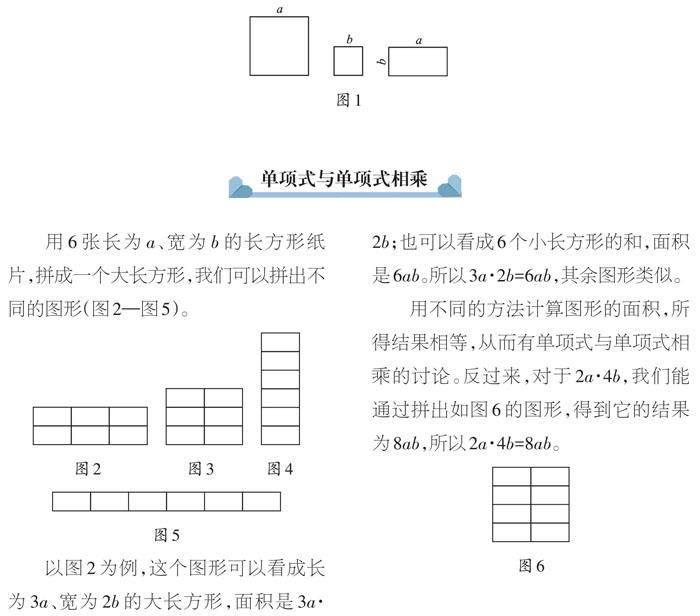
用6张长为a、宽为b的长方形纸片，拼成一个大长方形，我们可以拼出不同的图形（图2—图5）。

以图2为例，这个图形可以看成长为3a、宽为2b的大长方形，面积是3a·2b；也可以看成6个小长方形的和，面积是6ab。所以3a·2b=6ab，其余图形类似。

用不同的方法计算图形的面积，所得结果相等，从而有单项式与单项式相乘的讨论。反过来，对于2a·4b，我们能通过拼出如图6的图形，得到它的结果为8ab，所以2a·4b=8ab。

对于2a（3a+b），我们仍然用两个因式代表长方形的长和宽，拼出长为（3a + b）、宽为2a的长方形（如图7）。它由6个边长为a 的正方形和2个长为a、宽为b 的长方形拼成，所以它的面积可以表示为6a2+2ab。所以2a（3a+b）=6a2+2ab。

根据前面的经验，2a（3a-b）可用长为（3a-b）、宽为2a 的长方形表示。如何得到（3a-b）2呢？在3a的基础上减去b，我们可以采用覆盖的方法（如图8），未被遮盖的部分等于大的长方形的面积减去遮住的面积，所以，2a（3a-b）=6a2-2ab。

（a+b）（3a+b）可用长为（3a+b）、宽为（a+b）的长方形表示（如图9），它由3个边长为a的正方形及4个长为a、宽为b的长方形和1个边长为b的正方形拼成，面积可以表示为3a2+4ab+b2，所以（3a+b）（a+b）=3a2+4ab+b2。

類似地，（a+b）（3a-b）可用一边为（a+b）、另一边为（3a-b）的长方形的面积来表示（如图10），未被遮住的面积又可表示为3a2+3ab-ab-b2，所以（a+b）（3a-b）=3a2+2ab-b2。

我们除了用纸片直观地得出单项式乘单项式、单项式乘多项式、多项式与多项式的结果，还可以从运算的角度解释这些结果的合理性。例如，利用乘法交换律，将a与4交换，并将2与4相乘，即可得到2a·4b=8ab；利用乘法分配律，可得到2a（3a+b）=2a·3a+2a·b=6a2+2ab；同样，利用乘法分配律，将（a+b）看作一个整体，有（a+b）（3a+b）=（a+b）·3a+（a+b）·b=a·3a+b·3a+a·b+b·b=3a2+4ab+b2。

（作者单位：江苏省盐城市毓龙路实验学校）