对一个假命题教学的思考与探究——以“全等三角形”为例

◎ 上海外国语大学三亚附属中学 苏秀荣

在“全等三角形”教学中，许多教师习惯于从探究满足三个条件—“三边、三个角、两边一角或两角一边分别相等的两个三角形是否全等”，进而得出基本事实“SSS”“SAS”“ASA”和定理“AAS”，同时得出两个著名的假命题：“角角角”“边边角”。从教材而言，教材就是这样设计的，在“SSS”“SAS”“ASA”“AAS”之后，接着安排了“HL”，终止了系列研究；接着就是三角形全等知识的综合运用，不再考虑满足“边边角”的两个直角三角形、锐角三角形、钝角三角形是否全等，从知识的系统性、完整性来说，学生仅仅探究了一般情况下，满足两边和一边的对角对应相等的两个三角形不一定全等的情况，他们自然会想到：什么情况下它们全等？仅仅研究了满足三个条件时两个三角形是否全等的情形，自然会延伸到满足四个条件、五个条件的情形。如果探究教学到此戛然而止，学生的数学知识是支离破碎的，认知结构是缺损的。从数学思想方法而言，从一般的“边边角”是假命题，到特殊条件下是否是真命题，是一种从一般到特殊的思想方法；从通过作辅助线将锐角三角形、钝角三角形问题转化为直角三角形问题，又是一种转化的思想方法，而在将锐角三角形、钝角三角形问题转化为直角三角形问题研究时，还需要分类讨论的思想方法。这种探究学习，有助于学生领会这些数学思想方法的价值和作用，有利于探究思维能力的发展。

一、问题留白，为培养学生批判质疑的思维品质留下空间

师：我们都知道，“边边角”一般情况下是假命题，据此，你能提出一个有研究价值的问题吗？

生：“边边角”什么情况下是真命题？

师：这的确是一个值得研究的问题。回头看我们当初列举的反例，如图1，△ABC是一个钝角三角形，△BAD是一个锐角三角形，虽然满足“边边角”，但它们却不全等。由此，你又能提出一个怎样的问题？

图1

生：满足“两边及一边的对角对应相等”的两个锐角三角形全等吗？两个钝角三角形全等吗？

教师首先要明确哪里需要留白，如何让问题有效留白。其次，教师在提出问题时，要引领学生的提问，为学生提出有研究价值的问题埋下伏笔。“探究过程中的批判性思维是提升探究质量的必要条件与保障”，而提出问题恰恰是学生经历审视与质疑，比较、分析与评估，综合与判断的结果，是批判性思维的起点，教师的留白无疑催化了学生的批判质疑。

二、数学思想，为培养学生勇于探究的顽强意志提供“利器”

“工欲善其事，必先利其器。”数学思想方法是解决数学问题的“利器”。为何要转化？如何实现转化？这仍然需要教师的启迪与铺垫。

学生先独立思考，再小组交流，最后派代表发言。他们发现本题需要分类研究。分两种情况：已知两条直角边与一边的对角对应相等；斜边、一条直角边与一边的对角对应相等。前一种情况，可以利用“SAS”“ASA”或“AAS”证明两个三角形全等；后一种情况，可以利用“HL”或“AAS” 证明两个三角形全等，总之，满足“边边角”的两个直角三角形全等。

师：将一般问题特殊化的目的，一是看特殊情况下是否成立，如果特殊情况下不成立，那么一般情况下肯定不成立；二是若特殊情况下成立，我们就可以从中获得研究问题的方法和策略，进而将一般三角形问题转化为直角三角形问题研究。我们先研究满足“两边及一边的对角对应相等的两个锐角三角形是否全等”。

师：你认为接下去应该怎样研究？

学生经过尝试、深思、交流，最后得到本题无需分类，不妨假设AB=A′B′，AC=A′C′，∠B=∠B′，通过作BC、B′C′上的高将其转化为直角三角形问题，如图2。

图2

方法一：先利用“AAS”证明△ABD≌△A′B′D′，得到AD=A′D′，再利用“HL”证明Rt△ADC≌Rt△A′D′C′，得到∠C=∠C′，最后根据“AAS”证明△ABC≌△A′B′C′。

方法二：先利用“AAS”证明△ABD≌△A′B′D′，得 到AD=A′D′，BD=B′D′，再 利 用“HL”证 明Rt△ADC≌Rt△A′D′C′，得到DC=D′C′，所以，BC=B′C′，最后根据“SAS”或“SSS”证明△ABC≌△A′B′C′。

方法三：先利用“AAS”证明△ABD≌△A′B′D′，得 到AD=A′D′，∠BAD=∠B′A′D′，再 利 用“HL”证 明Rt△ADC≌Rt△A′D′C′，得 到 ∠DAC=∠D′A′C′，从而∠BAC=∠B′A′C′，最 后 根 据“ASA”或“AAS”证 明△ABC≌△A′B′C′。

①④习近平：《决胜全面建成小康社会夺取新时代中国特色社会主义伟大胜利》，人民出版社，2017年，第61、65—66页。②⑤⑥《中国共产党党务公开条例(试行)》，人民出版社，2017年，第1、9—10、3页。③《十八大以来重要文献选编》(上)，中央文献出版社，2014年，第23页。

乘胜追击，接着提出：“两边及一边的对角对应相等的两个钝角三角形全等吗？”

经过思考，学生发现：本题需要分类探究。可分为三种情况：①已知最大边、最大角与另一边对应相等；②已知最大边、另一边及这条边的对角对应相等；③已知较小的两条边及其中一边的对角对应相等。

已知钝角三角形△ABC与△A′B′C′中，AB=A′B′，AC=A′C′，∠C=∠C′，那么钝角三角形△ABC与△A′B′C′全等吗？

学生尝试了三种不同的作三角形高的方法：①如图3，作AC、A′C′上的高BD、B′D′；②如图4，作AB、A′B′上的高CD、C′D′；③如图5，作BC、B′C′上的高AD、A′D′，发现只有作BC、B′C′上的高AD、A′D′才能证明△ABC与△A′B′C′。

图3

图4

图5

通过上述问题解决的过程，学生得到了一条宝贵的经验：只要作第三边上的高就行了，接着，学生在图5中，作出了BC、B′C′上的高AD、A′D′；在图6中，作出了AB、A′B′上的高CD、C′D′。

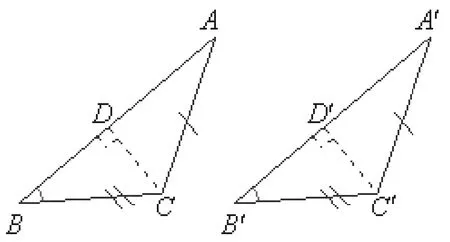
图6

总之，无论哪一种情况都能证明两个钝角三角形全等，由此，学生会得到：两边和一边的对角对应相等的两个钝角三角形全等。到此，教师继续提出：（1）根据刚才的研究，满足什么条件的“边边角”是真命题？（2）在将锐角三角形和钝角三角形通过作三角形一边上的高转化为直角三角形的过程中，辅助线作法有何共同特点？

这种反思性提问，有助于学生建立完整的认知结构，在更高的视域上建立知识间的联系，体会到了学习数学的乐趣。

三、链接中考，为培养学生理性思考的科学精神奠定基础

理性思维的重点是崇尚真知，追求真理。不唯书，不唯上，以敢于质疑的求是精神看待一切；尊重事实和证据，有严谨的治学态度；逻辑清晰严谨，能运用科学的思维方式认识事物、解决问题、指导行为，辩证地看待一切，具有辩证唯物主义视角。

师：下列两道中考题有正确答案吗？

①（2015·海南）如图7，下列条件中，不能证明△ABC ≌△DCB的是（ ）

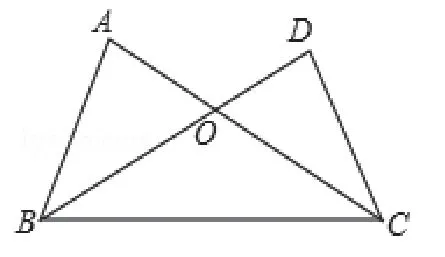
图7

A.AB=DC，AC=DB B.AB=DC，∠ABC=∠DCB

C.BO=CO，∠A=∠D D.AB=DC，∠A=∠D

②（2016·金华）如图8，已知∠ABC=∠BAD，添加下列条件还不能判定△ABC ≌△BAD的是（ )

图8

A.AC=DB B.∠CAB=∠DBA

C.∠C=∠D D.BC=AD

经过思考，学生认为这两题都没有正确答案，因为，“如图6”本身说明了图中要证明的两个三角形都是锐角三角形，即使在满足“边边角”的情况下，两个锐角三角形仍然全等。

这种问题设计有助于培养学生不畏权威的探究意识，独立思考的批判精神，求真务实的科学态度，理性思考的科学精神。

总之，在数学教学中，教师应该有宽阔的教育视野，博大的人文胸襟，应该着眼于学生未来的发展与社会需要，立足于核心素养的培养，因为数学核心素养是“求木之长者”之“根本”，“欲流之远者”之“泉源”。