基于FCPN的离散制造系统质量风险分析评估研究

赵家黎 吴丹 郜肖盼 代燕霞

作者简介：赵家黎（1980—），男，教授，博士学位，研究方向为数控技术、精密测量、复杂制造过程质量控制。

基金项目：国防科技工业局国防基础科研计划（JCKY2019427D002）。

参考文献引用格式：

赵家黎， 吴丹， 郜肖盼， 等. 基于FCPN的离散制造系统质量风险分析评估研究[J]. 汽车工艺与材料， 2024（5）： 49-58.

ZHAO J L， WU D， GAO X P， et al. Research on Quality Risk Analysis and Evaluation of Discrete Manufacturing Systems Based on FCPN[J]. Automobile Technology & Material， 2024（5）： 49-58.

摘要：针对离散制造系统随机性、多样性以及复杂性的特点，高效、准确地识别系统质量风险因素并进行质量风险量化评估是制定相应质量控制活动、提高产品质量的关键。为此，首先构建模糊着色Petri网的产品质量风险评估模型。然后，确定模糊推理规则，并通过现场获取的置信度经验值进行模糊推理，计算得出中间库所和终止库所的置信度。最后，以汽车顶盖冲压工艺过程为例进行分析，验证了该模型的合理性，并且可推广应用到其他同类离散制造过程。

关键词：离散制造系统 顶盖冲压工艺过程 模糊着色Petri网 质量风险评估

中图分类号：TH18；TP31   文献标志码：B   DOI： 10.19710/J.cnki.1003-8817.20230353

Research on Quality Risk Analysis and Evaluation of Discrete Manufacturing Systems Based on FCPN

Zhao Jiali， Wu Dan， Gao Xiaopan， Dai Yanxia

（School of Mechanical and Electronical Engineering， Lanzhou University of Technology， Lanzhou 730050）

Abstract： In view of the characteristics of randomness， diversity and complexity of discrete manufacturing systems， efficiently and accurately identifying system quality risk factors and conducting quantitative assessment of quality risks are crucial to developing corresponding quality control activities and improving product quality. In this research， firstly a product quality risk assessment model for Fuzzy Colored Petri Nets was constructed. Then the fuzzy inference rules were determined， and the confidence of the intermediate library and the terminating library was calculated by fuzzy reasoning through the confidence empirical value obtained at the scene. Finally， the automotive top cover stamping process was analyzed as an example to verify the rationality of the model proposed in this paper， which can be applied to other similar discrete process manufacturing.

Key words： Discrete manufacturing systems， Top cover stamping process， Fuzzy colored Petri nets， Quality risk assessment

1 前言

離散制造系统的产品由多个零件经过不连续工序的加工最终装配而成，产品工艺流程具有质量风险因素多、难以控制的特点[1]。质量是企业核心竞争力的关键，因此，实施质量风险评估能够改进企业质量管理活动，提高产品质量。

针对风险研究，国内、外学者针对险评价指标体系构建和风险建模进行了大量研究。Cheng等[2]提出网络风险分析框架；Zegordi等[3]基于Petri网理论，跟踪供应链网络物流的风险进行仿真验证；杨康[4]构建供应链网络风险传播的SIS-RP模型；李远远等[5]构建ANP-Fuzzy模型，评价农业供应链中存在的风险；王秋莲[6]通过对全生命周期的分析指出再制造系统面临的各种风险，并构建评价指标体系。

对风险进行识别并对其进行评价和建模主要在于解决定量化分析质量风险。Petri网理论作为描述制造系统的可视化工具，利用网进行制造系统建模，可以清晰地描述系统各状态之间的动态转移过程。Zhou等[7]利用Petri网建立了柔性装配生产模型，并用随机Petri网对其进行性能分析。王化冰[8]通过分析制造系统加工过程，建立系统的Petri网模型。

传统的Petri网无法描述模糊指标，为解决风险的模糊不确定性、降低模型的复杂度，引入模糊着色Petri网模型。Looney[9]于1988年首次提出基于模糊推理的模糊Petri网建模方法。2014年，詹盛等[10]根据车辆不同时间的状态建立模糊规则，构建隶属度函数和模糊着色Petri网模型。张新菊等[11]综合研究了多状态系统，提出模糊着色Petri网（Fuzzy Colored Petri Nets，FCPN）模型描述可靠性特征，此方法逐渐拓展、应用到风险评估领域。

综上，国内外学者对制造系统评价的研究已经比较全面，涵盖服务型制造系统、柔性制造系统等，但内容大多集中于汽车产业组织创新、客户参与产品全生命周期、供应链、生产过程故障预测等，分析制造业服务化以及制造系统风险，制造系统对产品质量的影响研究较少。

为解决离散制造系统质量风险的模糊不确定性，降低模型的复杂度，本文提出基于模糊着色Petri网的风险评估方法，根据评价问题的设置构成质量风险评价指标体系，将反映质量风险的综合评价指标按照不同属性进行层次分组，并以汽车制造系统中外覆盖件冲压工艺过程为例进行验证。

2 基于模糊着色Petri网的产品质量风险评估模型

2.1 模糊着色Petri网的结构

通过分析离散制造系统中工作流、物质流、信息流的层次结构和功能，明确能够总体反映质量风险评价体系的问题，并由最高层和第1层构成。质量风险复杂的评价体系对应的评价指标层次也相对复杂。按照推理深度划分Petri网层级数量为m，添加辅助库所和辅助变迁，构建多层级网络结构[12-14]。

将模糊着色Petri网定义为14元组，即：

FCPN=（P，T，D，C，I，A，N，W，F，CF，α，β，th，θ），且满足以下条件：

a. P={PC，PF}为库所的有限集，PC={pc1，pc2，...，pck}为控制库所集，PF={pf1，pf2，...，pfm}为模糊库所集，PC∩PF=?；

b. T={TC，TF}为变迁的有限集合，TC={tc1，tc2，...，tcm}（m≥0）为有限控制库所集，TF={tf1，tf2，...，tfn}（n≥0）为有限模糊变迁集，TC∩TF=?；

c. D为命题的有限集；

d. C为库所和变迁到颜色映射的有限集合；

e. I为关联矩阵；

f. A={α1，α2，...，αk}为弧的有限集合；

g. N为节点函数A→（P×T∪T×P）；

h. W为权重集合；

i. F为模糊集合；

j. CF={cf1，cf2，...，cfm}为置信因子集合；

k. α为库所的关联函数P→[0，1]；

l. β为从库所P到命题D集合的双向映射P→D；

m. th={λ1，λ2，...，λs}为阈值集合；

n. θ=（θp1，θp2，…，θpM）T为命题的置信度。

其中，置信度向量的计算公式为[15]：

[θ*k=θk-1（Ok-1?Rk-1）（ITk-1θk-1）*]       （1）

式中：O为M×N的矩阵，M为库所的数量，N为迁移的数量，R为表示迁移可信度的三角矩阵，k为1～m范围内所取的正整数，其他运算符号的含义如表1所示。

2.2 推理模型

在模糊推理规则的基础上，结合FCPN的规则和变量，将模糊着色Petri网定义为14元组FCPN。依据不同颜色表示模糊规则库的不同变量，对列出的评价指标进行排列。将形成质量风险多层级的评价指标体系划分层级、添加辅助库所并且变迁后可得如图1所示的FCPN模型。

2.2.1 基于规则的FCPN模型

合并同类规则能够有效降低有色Petri网系统的复杂度，使用不同颜色的托肯进行区分，缩小系统规模，简化后的形式推理模型如图1a所示。

2.2.2 基于变量的FCPN模型

根据Petri网特有的图形化表达特征，不同颜色表示模糊规则库的不同变量，不同规则中的同一变量用该变量的颜色集表示，最终构建的模型如图1b所示。

2.3 风险评估模型

风险评估模型运用了一些必要的假设和简化，采用适当的语言符号、数学符号和数学工具构成数学结构。风险评估模型主要用于解释风险特定现象的現实状态，评估或决策质量风险项目的当前和未来状态，给出最优的评估和决策方案。FCPN产品质量风险评估方法可以目的明确地进行质量管控。FCPN模型如图2所示，具体的评估过程步骤如下：

a. 分析系统能够明确系统中工作流、物质流、信息流的层次结构和功能，辨识系统风险并将专家知识表示为IF（命题置信度）THEN ?（变迁置信度R）模糊推理规则的形式；

b. 根据FCPN的定义将模糊推理规则表示为Petri网模型，并对不同流过程要素进行着色分类；

c. 按照推理深度划分Petri网层级数量m，添加辅助库所和变迁，构建多层级网络结构；

d. 根据式（1）计算θk（1≤k≤m），得到目标层级的输出库所对应命题的置信度。

3 顶盖冲压工艺过程质量风险评估建模

3.1 顶盖冲压工艺过程质量风险分析

汽车整车制造过程属于典型的离散制造系统，顶盖冲压工艺过程作为关键环节存在着众多质量风险点，冲压过程中质量的稳定性直接关系到后续工艺的顺利进行和最终产品质量。本文以H企业某型号轿车的外覆盖件冲压工艺过程为研究对象，在汽车整车制造过程中，H企业某型号轿车的天窗（三厢车）顶盖冲压工艺过程如图3所示。

3.2 模型构建

从过程流的角度对顶盖冲压工艺进行分析发现，物质流（如残次品流入下游工序）、工作流（如拉伸、修边等工位）和信息流（如检验设备出现故障、清洗环境不达标）之间错综交互。因此，根据顶盖冲压工艺成形过程中的相互影响，结合现场调研和专家知识，得到模糊推理规则如下：

a. 检查人员操作不当或检验设备出现故障导致残次品流入下游工序；

b. 清洗环境不达标导致冲压件表面附着杂质；

c. 刃口磨损、导向精度差或凹凸模的位置不同心导致毛刺过大；

d. 孔距太小或间隙过大导致变形；

e. 操作员操作时存在拖、拉等动作或剪切过程出现划伤导致表面划伤；

f. 上料不到位或定位装置故障或松动导致尺寸不符；

g. 材料表面臟或润滑油有杂质导致鼓包或凹坑；

h. 定位不准或压边力过大导致拉裂；

i. 定位不准导致翻边高度不一致；

j. 凹凸模间隙过大或落料尺寸不准导致翻边不垂直；

k. 原材料本身强度差或板料变形量不足导致生产成品刚性不足。

根据上述推理规则和风险评估模型进行FCPN建模，需要添加辅助库所和变迁来构建多层级网络结构，模型如图4所示，库所代表的含义如表2所示。

3.3 推理运算

根据因素发生的可能性程度对因素发生的模糊概率进行置信区间划分，如表3所示。基于现场调研和专家知识描述获得初始事件和规则的发生概率，确定置信度的经验值，得到顶盖冲压工艺模型中初始库所置信度和所有变迁置信度，如表4、表5所示。

根据式（1），当k=1时，输入库所有P1、P2、P3、P4、P5，输出库所有[P6、P7、P′4、P′5、P″5]，计算参数为：

θ0=[[P1，P2，P3，P4，P5，P6，P7，P′4，P′5，P″5]]T               （2）

经计算，θ0=[0.36，0.27，0.30，0.29，0.41，0，0，0，0，0，0]T，[I0=100000010000001000000100000010000000??????00000010×6]，[O0=000000??????00000011000000100000010000001000000110×6]，

R0=diag（0.40，0.38，0.35，0.44，0.50，0.66）。

则根据式（1）计算出θ1为：

[θ*1=θ*0（O0?R0）（IT0θ0）*]          （3）

经计算，θ1=[0.35，0.23，0.44，0.4，0.55，0.158，0.036，0.16，0.205，0.168]T。

由此可得，中间库所P6、P7、[P′4]、[P′5]、[P″5]的置信度分别为0.158、0.036、0.160、0.205、0.168。

当k=2时，根据式（1）计算出θ2为：

[θ*2=θ*1（O1?R1）（IT1θ1）*]           （4）

经计算，θ2=[0.102，0.2231，0.2109，0.101，0.128，0.019，0.0113，0.1002，0.132，0.2011，0.1378，0.091，0.153，0.122，0.1874，0.1866，0.2053，0.248，0.136，0.138，0.120，0.118]T。

由此可得，中间库所P21、P23、P24、P25、P26、P27、P28、P29、P30的置信度分别为0.122、0.1874、0.1866、0.2053、0.248、0.136、0.138、0.120、0.118。

当k=3时，根据式（1）计算出θ3为：

[θ*3=θ*2（O2?R2）（IT2θ2）*]          （5）

经计算，θ3=[0.135，0.312，0.4441，0.1963，0.2031，0.1332，0.231，0.1981，0.0911，0.1065，0.0598，0.2503，0.1651]T。

由此可得，终止库所P31（产品刚性不足）、P32（表面质量缺陷）、P33（尺寸不一）的置信度分别为0.0589、0.2503、0.1651。

3.4 风险评估结果分析

根据上述分析可以看出，在对产品质量产生影响的30个因素中，工作流因素有17个（占56.7%），物质流因素有5个（占16.6%），信息流因素有8个（占26.7%），工作流对应库所的概率最大，信息流对应库所的概率次之，物质流对应库所的概率最小。此外，由风险因素所对应的初始库所情况可知，作业流因素所含风险因素最多，占所有初始库所的57.9%，信息流因素次之，占比为31.6%，物质流因素所含风险因素最少，占比为10.5%。上述结果表明，在顶盖冲压工艺过程中，对产品质量产生影响的因素是工作流，其次是信息流，最后是物质流。因此，在顶盖冲压工艺工程产品质量管控中，质量风险管理的首要工作是工作流的跟踪和管控，还需加强生产信息的交流，使其和生产状态同步流通，才能保证顶盖冲压工程中的产品质量。

4 生产环节风险评估建模

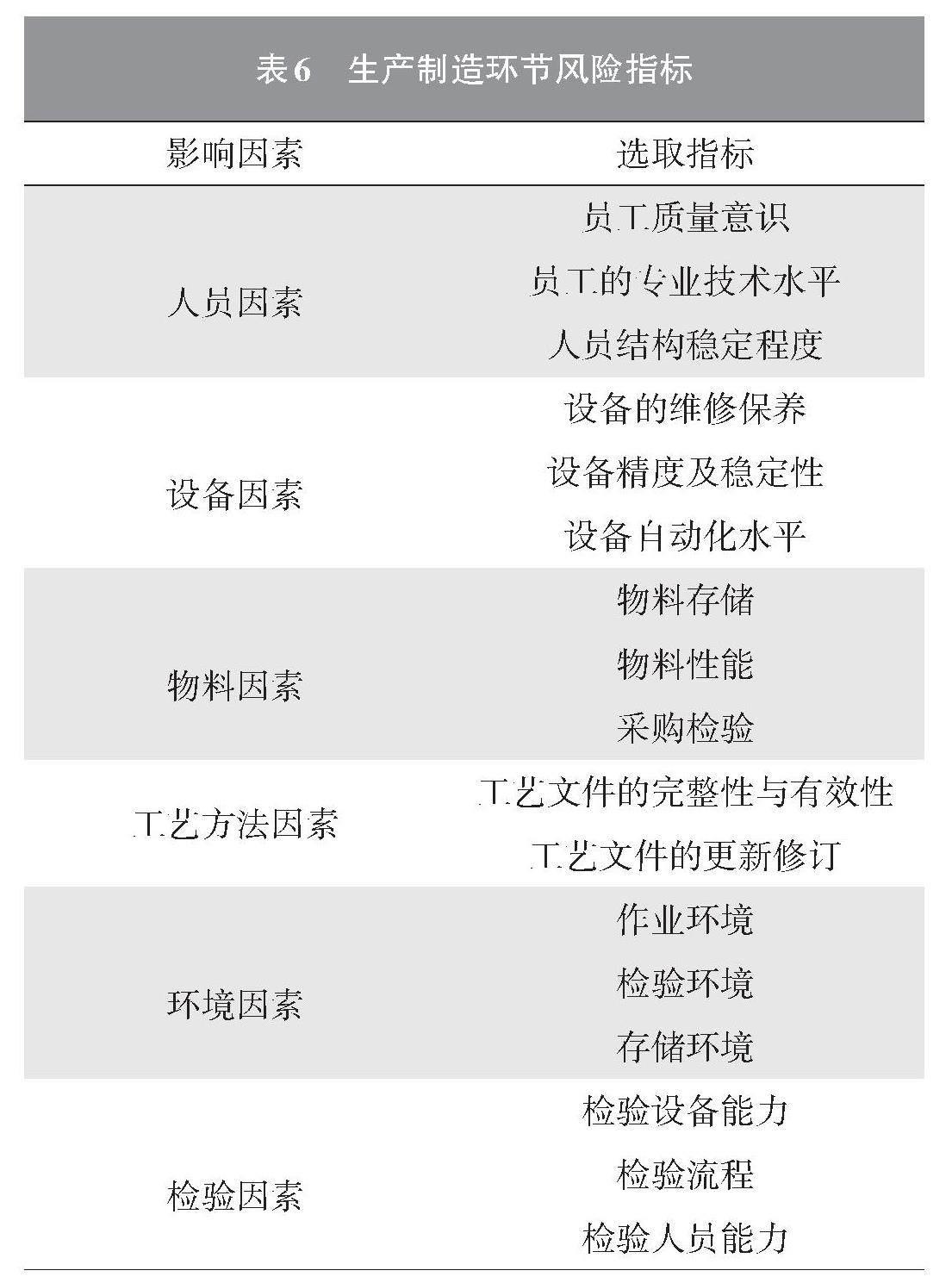
4.1 指标选取

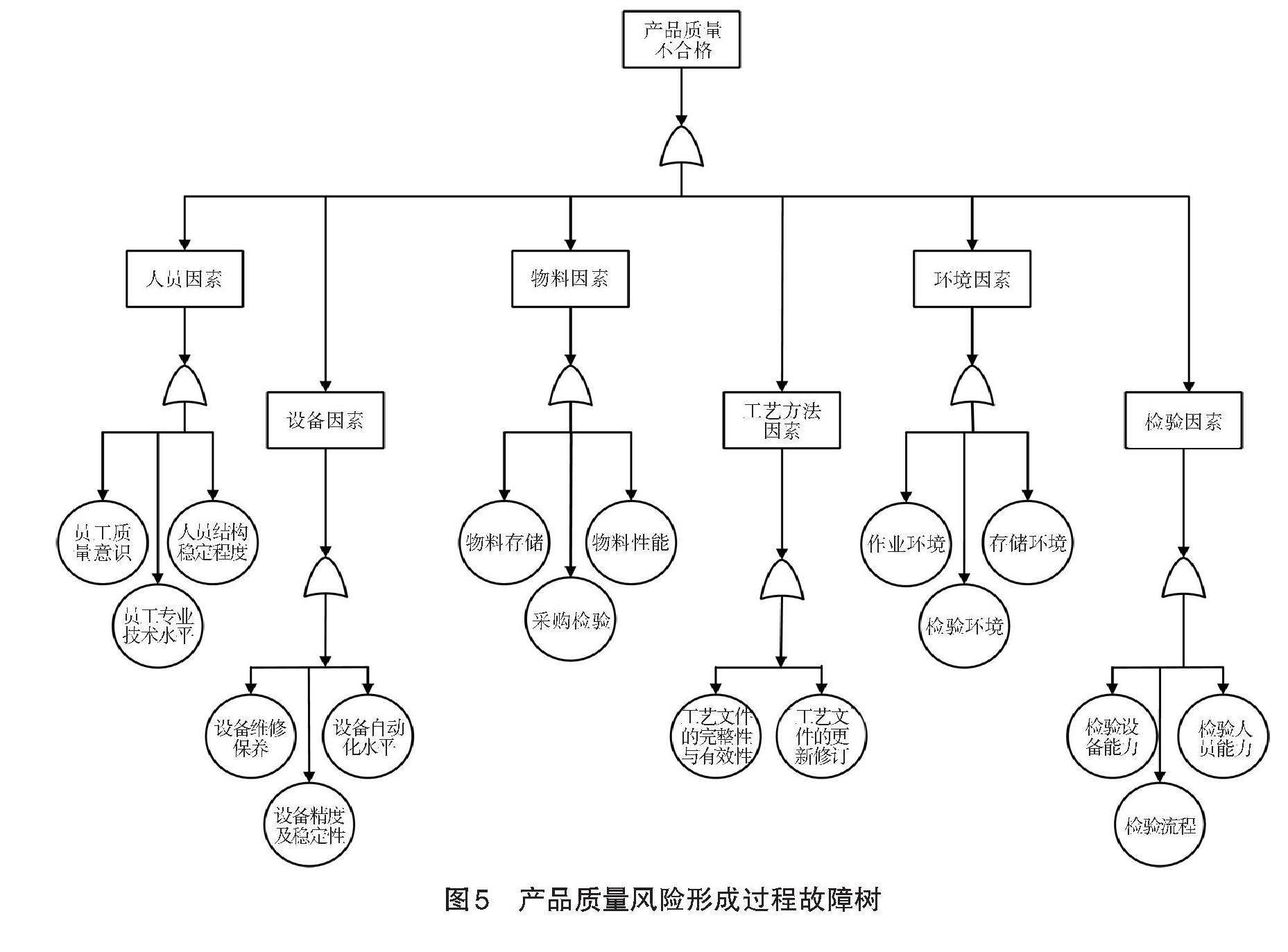
以产品生产制造工程中存在风险因素为指标，进行更加合理科学的评估，最终选取的指标如表6所示，用故障树描述对H企业整车制造产品制造阶段的产品质量的风险形成过程，如图5所示。

4.2 构建模型

根据图6的转化规则，将产品质量风险形成过程的故障树转化为模糊着色Petri网。

根据上述的转化规则，对H企业产品质量风险形成过程的故障树进行转化，根据H企业整车制造产品制造系统的特点，结合现场调研结果和专家知识，得到推理规则如下：

a. 若由于员工质量意识薄弱、人员结构波动、员工专业技术水平不够导致错误发生错误，进入factor-human节点与factor-human后未解决，则显示P-failed；

b. 若由于设备未按标准维修保养、设备自动化水平落后或设备稳定性弱且精确度不高导致发生错误，进入factor-machine节点与 factor-machine后未解决，则显示P-failed；

c. 若由于物料储存不当、采购检验流程不规范或物料性能不达标导致发生错误，进入factor-material节点与 factor-material后未解决，则显示P-failed；

d. 若由于工艺文件的更新修订跟不上产品实际生产所要求的标准或工艺文件不完整、失去有效性导致发生错误，进入factor-method节点与factor-method后未解决，则显示P-failed；

e. 若由于作业环境、存储环境或检验环境达不到生产要求导致发生错误，进入factor-setting节点与 factor-setting后未解决，则显示P-failed；

f. 若由于检验流程不规范、检验设备落后、检验人员专业能力不达标或工作疏忽导致发生错误，进入factor-checking节点与 factor-checking后未解决，则显示P-failed；

利用上述推理规则进行建模，产品制造过程的产品质量风险系统的FCPN模型如图7所示。

模型中库所、变迁及其各自所代表的意义如表7、表8所示。

基于现场调研和专家知识描述，获得初始事件与规则的发生概率，确定置信度的经验值，得到模型中的初始库所置信度与所有变迁的置信度，如表9所示。

根据式（1），当k=1时，输入库所有P1、P2、P3、P4、P5、P6、P7、P8、P9、P10、P11、P12、P13、P14、P15、P16、P17，输出库所有factor-human、factor-machine、factor-material、factor-method、factor-setting、factor-checking，则计算参数为：

θ0=[P1，P2，P3，P4，P5，P6，P7，P8，P9，P10，P11，P12，P13，P14，P15，P16，P17，factor-human，factor-machine，factor-material，factor-method，factor-setting，factor-checking]T     （6）

經计算，θ0=[0.20，0.15，0.46，0.24，0.20，0.32，0.22，0.18，0.48，0.42，0.48，0.44，0.32，0.30，0.25，0.26，0.30，0，0，0，0，0，0]T，[O0=00000000000000000?????????????????11100000000000000000111000000000000000001110000000000000000011000000000000000001110000000000000000011123×17]，

[I0=1000000000000000001000000000000000001000000000000000001000000000000000001000000000000000001000000000000000001000000000000000001000000000000000001000000000000000001000000000000000001000000000000000001000000000000000001000000000000000001000000000000000001000000000000000001000000000000000001?????????????????0000000000000000023×17]，

R0=diag（0.40，0.28，0.85，0.66，0.52，0.68，0.55，0.28，0.85，0.86，0.86，0.75，0.65，0.65，0.46，0.48，0.60）。

根据上述参数以及式（1）计算出θ1为：

[θ1=θ0（O0?R0）（IT0θ0）]           （7）

经计算，θ1=[0.36，0.55，0.54，0.44，0.36，0.60，0.38，0.40，0.66，0.52，0.66，0.56，0.60，0.62，0.45，0.58，0.62，0.169，0.188，0.135，0.254，0.28，0.24]T。

由上述计算结果可得中间库所factor-human、factor-machine、factor-material、factor-method、     factor-setting、factor-checking的置信度分别为：0.169、0.188、0.135、0.254、0.28、0.24。

当k=2时，同理可根据式（1）计算出θ2为：

[θ2=θ1（O1?R1）（IT1θ1）]            （8）

经计算，θ2=[0.1966，0.25，0.48，0.36，0.38，0.20，0.118]T。

表10为H公司产品质量风险的评估值、评估值与真实值的相对误差。

4.3 模型性能评价

选取均方根误差RSME、均方误差MSE、平均绝对百分比误差MAPE和平均绝对误差MAD判定FCPN模型评估的精确性。

均方根误差RSME为：

[RMSE=i=1n（yi-yi）2n]                        （9）

均方误差MSE为：

[MSE=1ni=1n（yi-yi）2]                    （10）

平均绝对百分比误差MAPE为：

[MAPE=i=1nyi-yiyin]                    （11）

平均绝对误差MAD为：

[MAD=i=1nyi-yin]                    （12）

对模型所产生的的评估值数据进行统计学的评估误差判定，结果如表11所示。

5 结束语

对顶盖冲压工艺流程进行研究，通过现场调研和专家知识，从作业流、信息流和物质流入手，得到模糊推理过程并构建模糊着色Petri模型，采用推理运算得到风险评估结果；针对生产制造环节，利用故障树表示生产制造过程的质量风险形成过程，并转化为模糊着色Petri网。根据RMSE、MSE、MAPE和MAD判定模型的评估性能，由判定结果可知：FCPN模型的评估结果与实际值的平均相对误差为9.97%，可以得出，FCPN模型的评估可行度较高，证实了评估模型的科学性和有效性。

参考文献：

[1] 王加兴. 离散制造车间数据采集及其分析处理系统研究与开发[D]. 杭州：浙江大学， 2010.

[2] CHENG S K， KAM B H. A Conceptual Framework for   Analysing Risk in Supply Networks[J]. Journal of Enterprise Information Management， 2008， 21（4）： 345-360.

[3] ZEGORDI S H， DAVARZANI H. Developing a Supply Chain Disruption Analysis Model： Application of           Coloured Petri-nets[J]. Expert Systems with Applications， 2011， 39（2）： 2102-2111.

[4] 楊康， 张仲义. 基于复杂网络理论的供应链网络风险传播机理研究[J]. 系统科学与数学， 2013， 33（10）： 1224-1232.

[5] 李远远， 刘礼帅. 基于ANP-Fuzzy模型的农产品供应链风险评价研究[J]. 数学的实践与认识， 2017， 47（13）： 24-32.

[6] 王秋莲. 基于神经网络的再制造系统风险评价[J]. 科技广场， 2010， 3（8）： 215-217.

[7] ZHOU M C， LEU M C. Modeling and Performance       Analysis of a Flexible PCB Assembly Station Using Petri Nets[J]. Journal of Electronic Packaging， 1991， 113（4）： 410-416.

[8] 王化冰. 一种基于同步合成Petri网的FMS建模方法[J]. 系统工程理论与实践， 2001， 21（2）： 35-42.

[9] LOONEY C G. Fuzzy Petri Nets for Rule-Based Decisionmaking[J]. IEEE Transactions on Systems， Man， and       Cybernetics： Systems， 1988， 18（1）： 178-183.

[10] 詹盛， 徐远新， 石涌泉， 等. 基于模糊着色Petri网的车辆运动轨迹预测[J]. 计算机工程与应用， 2014， 50（3）： 227-231.

[11] 张新菊， 姚淑珍. 基于模糊着色Petri网的多状态系统可靠性分析[J]. 计算机科学， 2016， 43（11）： 77-82+101.

[12] 张鹏程， 李人厚， 秦明， 等. 模糊着色Petri网及其在工作流建模中的应用[J]. 计算机辅助设计与图形学学报， 2002（8）： 713-716.

[13] 陈亚华， 吴时霖. 基于模糊有色Petri网的不确定性学习和推理方法[J]. 系统仿真学报， 2003（1）： 56-58.

[14] 程静静， 张圆刚. 基于模糊数学和灰色理论的多层次旅游村发展综合评价[J]. 统计与决策， 2016（2）： 186-188.

[15] 李威君， 刘双磊， 伊岩， 等. 基于多层级模糊着色Petri网的输气站排污系统风险评估[J]. 安全与环境学报， 2022， 224（4）： 1736-1742.