近年多省联考数学试题分析及教学建议

作者简介：黄邵华，1985年生，福建南平人，硕士研究生，高级教师，主要研究方向为中学数学教育教学。

摘 要：在推进高考综合改革进程中，教育部组织了多次联考，为各省（区、市）新高考落地保驾护航。在广西新高考即将落地之际，分析高考适应性演练中的试题具有非常重要的指导意义。多省联考试题与当年高考数学试题关系密切，根据2024年1月进行的九省联考的数学试题情况，教师指导学生备战2024年高考应关注试卷新结构并指导学生及时适应、关注非主干知识的工具性、重视训練解答具有创新性和探究性的问题。

关键词：联考；试题分析；数学高考；教学建议

中图分类号：G63 文献标识码：A 文章编号：0450-9889（2024）08-0058-05

2024年1月，为了提前适应新高考的考试题型和考试模式，教育部组织全国第三批启动高考综合改革试点的安徽、黑龙江、吉林、江西、甘肃、广西、贵州，以及后来相继宣布加入的河南和新疆等九个省区，共同进行了一次大规模的2024年新高考适应性演练，俗称九省联考。事实上，这并不是教育部第一次组织高考适应性演练，早在2021年，教育部就组织了河北、辽宁、江苏、福建、湖北、湖南、广东、重庆8个省市的八省联考，在2023年又组织了云南、吉林、黑龙江、安徽四个省份的四省联考。本文通过分析2021年的八省联考、2023年的四省联考数学试题与当年高考数学新课标卷之间的关联，以及分析2024年九省联考数学试题，提出一些高考数学复习备考建议。

一、多省联考与当年高考数学试题关联分析

近年的多省联考中语文、数学、英语试题由教育部组织命题，命制多省联考试题时和命制高考试题一样要遵循《中国高考评价体系》以及普通高中课程标准，那么多省联考和当年的高考试题之间有什么关联？多省联考试题是否释放出一定的信号？如何通过多省联考试题引导高三备考教学？不少高中一线数学教师都存在诸如此类的困惑。

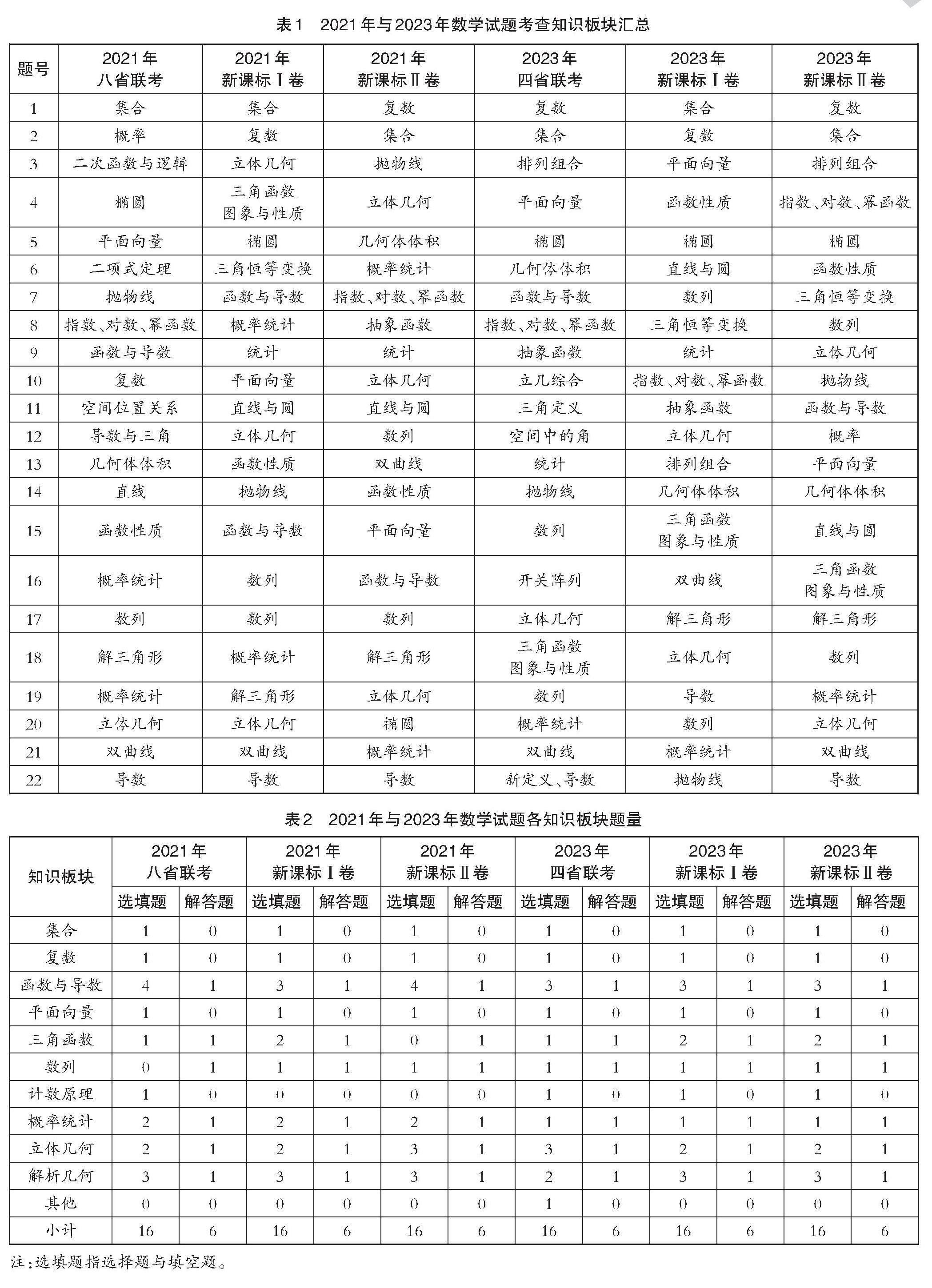
首先，我们从考查的知识板块层面，将2021年的八省联考和2023年的四省联考数学试题与当年的高考新课标Ⅰ卷和Ⅱ卷进行整理，得到各知识板块考查汇总表（如下页表1所示）。

为方便观察和了解联考试题与高考试题对各知识板块的考查情况，笔者整理、汇总出这两次联考试题与当年高考试题各题型考查相关知识板块的题量（如下页表2所示）。

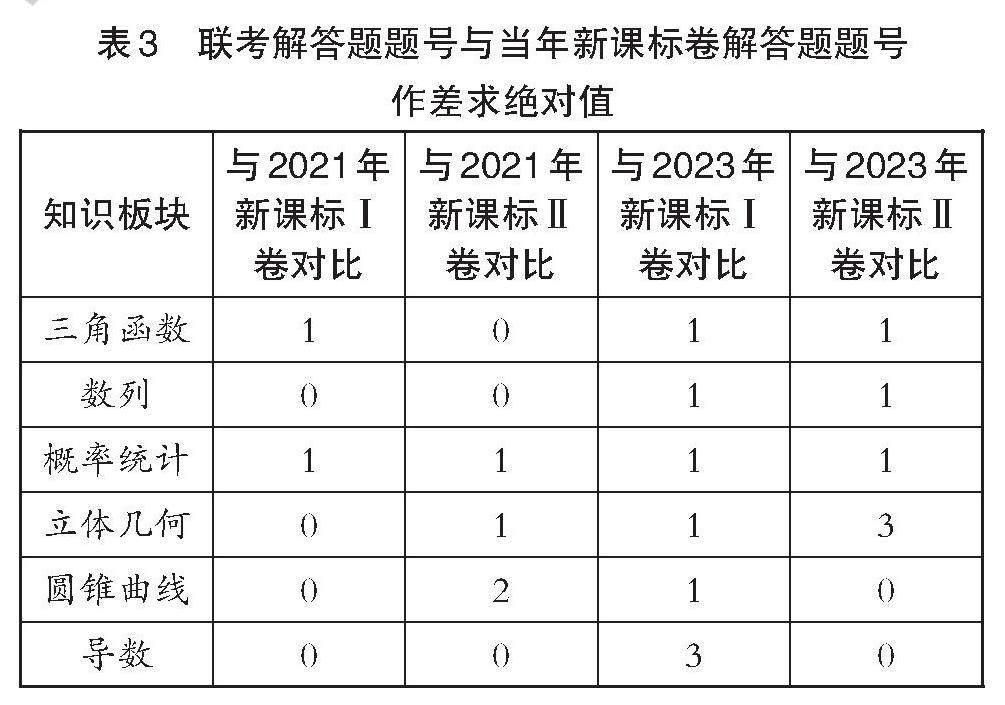
先分析解答题。从表2可以看到，每年联考的解答题涉及的知识板块和最终的高考新课标卷是完全一致的，即传统的三角、数列、概率统计、立体几何、解析几何、导数六大板块。再观察表1，2021年新课标Ⅱ卷和2023年新课标Ⅰ卷都将概率统计题编排在第21题，难度较大，相对之前多年高考试卷将圆锥曲线和导数放在最后两题而言，还是有些变化的。我们再将联考解答题各板块试题题号与当年高考题各板块试题题号作差求绝对值，得到第60页表3。从表3中不难看出，联考数学解答题与当年高考数学解答题，考查各知识板块的题号差大多不超过1（占比87.5%），可见联考解答题中考查各知识板块试题所处的位置和当年高考试卷基本一致。也就是说，这两次联考解答题和当年高考解答题的考查知识板块完全一致，且各板块知识在本卷中的考查难度也基本相同，但可能在个别板块上会有较大的难度调整。

再分析选择题与填空题。观察表2可以发现，每年的高考题考查各知识板块知识的题数，也就是所占分值，和当年联考试题几乎保持一致。2023年新课标Ⅰ卷相对当年的联考卷，多了三角函数和解析几何题，少了立体几何和创新题。

综合以上分析，2021年与2023年的联考数学试题对比当年的高考数学试题，有以下几个特点：一是试题的整体结构、题量、题型及各题型分值均完全一致；二是解答题考查的六个知识板块完全一致，各知识板块试题的题号也基本一致；三是选择题、题空题在各个知识板块所占的题量、分值基本一致，只在少数板块上有所调整。

特别强调一点，虽然联考题与当年高考题有以上诸多近似，但是有一点却有较大差异，就是试题的难度。例如，2023年的四省联考试题，难度明显较大，当年联考结束后，考生普遍愁眉苦脸，同时也引发全国范围内广大一线教师的热烈讨论。紧接着，因为这次联考所谓“释放出来的信号”，各地的高考模拟题瞬间加大难度。但事实上，2023年新课标Ⅰ卷和Ⅱ卷，整体比较平稳，试题难度也适中，并没有刻意加大难度。

二、2024年九省联考数学试题分析

2024年1月19日下午，九省联考数学试题公开，立即引发了广泛关注。有教师称之为高考数学试题结构的一次“颠覆性调整”，其在试题结构和分值等方面主要有以下四个变化：一是全卷题量由原来的22道题减少为19道题；二是单选题数量不变还是8道，但是多选题、填空题以及解答题各减少1道，也就是题型结构由原来的“8+4+4+6”，变为“8+3+3+5”；三是单选题和填空题每题分值不变，依然是5分，但多选题每道题分值由原来的5分增加至6分，解答题虽然减少了1道题，但总分却增了7分，由原来的70分增加到77分；四是解答题各小题分值由原来的“10+12+12+12+12+12”，改变为“13+15+15+17+17”。

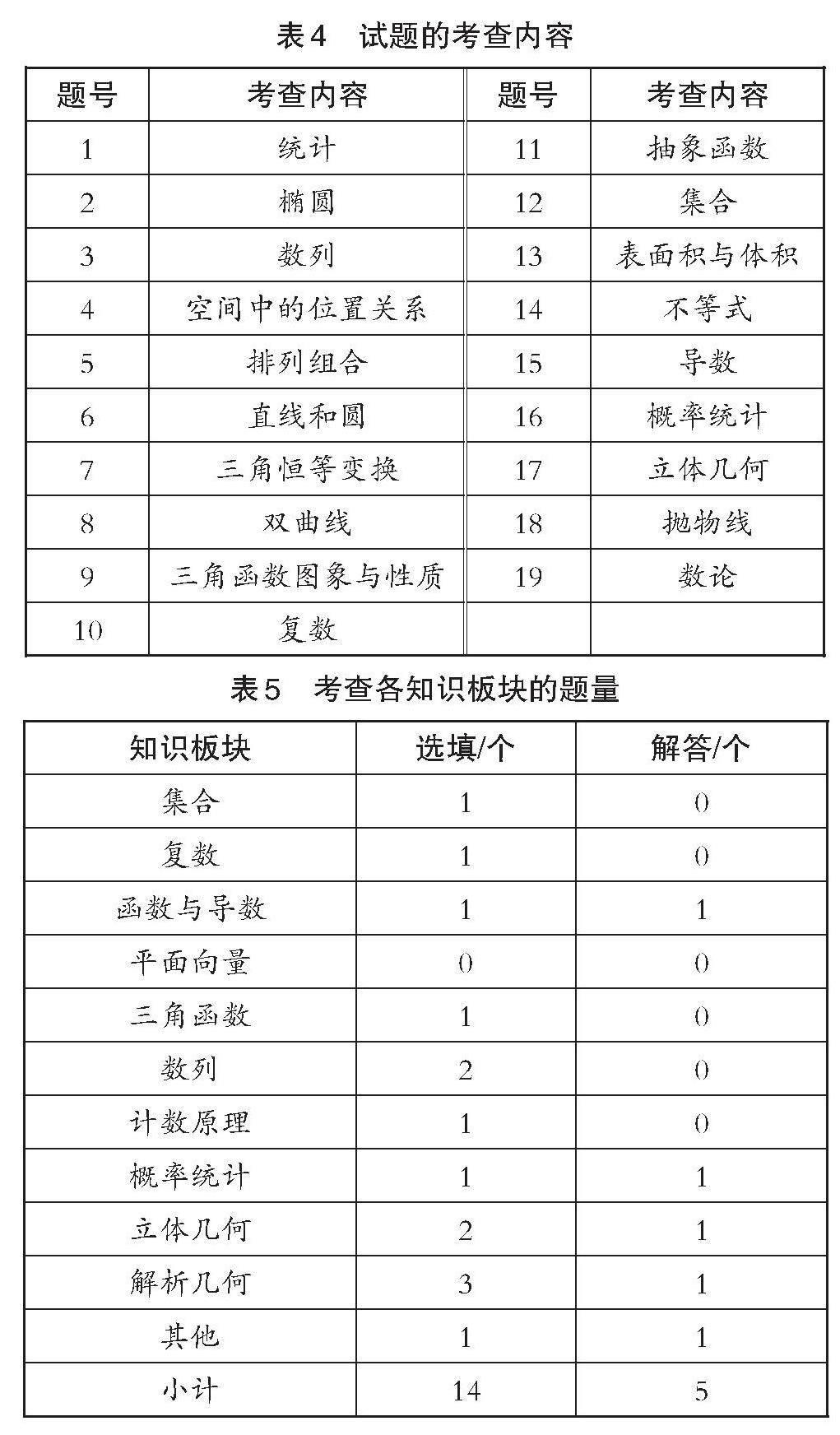
以上是题型结构和分值上的变化，我们再来分析各题考查的知识板块情况。笔者整理各题考查的内容与考查各知识板块的题量，得到表4、表5。

表4 试题的考查内容

[题号 考查内容 题号 考查内容 1 统计 11 抽象函数 2 椭圆 12 集合 3 数列 13 表面积与体积 4 空间中的位置关系 14 不等式 5 排列组合 15 导数 6 直线和圆 16 概率统计 7 三角恒等变换 17 立体几何 8 双曲线 18 抛物线 9 三角函数图象与性质 19 数论 10 复数 ]

表5 考查各知识板块的题量

[知识板块 选填/个 解答/个 集合 1 0 复数 1 0 函数与导数 1 1 平面向量 0 0 三角函数 1 0 数列 2 0 计数原理 1 0 概率统计 1 1 立体几何 2 1 解析几何 3 1 其他 1 1 小计 14 5 ]

由表4、表5可以看出这份联考试题相对以往的高考题，有以下六个明显的变化。

一是第1题、第2题单项选择题不再是考查集合和复数，而是考查统计和圆锥曲线；对集合的考查放在了第12题，也就是填空题第1题，对复数的考查放在了第10题，也就是多选题第2题，考查难度均有所提升。

二是虽然近三年新课标卷必出现一道平面向量题，但是这次并没有出现以平面向量为完整背景的题目；而近年高考在选择题、填空题中考查的重点板块知识——函数与导数，只出现了1道题，也就是第11题——多选题最后一题，考查的是抽象函数。可见此次九省联考减少的3道选填题，主要是减少了针对向量和函数的考查。但是，这并不代表削弱向量和函数，事实上，选择题的第6题和第8题分别考查了向量的坐标和向量的数量积，而第9题、第12题、第14题、第18题等涉及求解最值的问题中，都用到了函数的思想，因此，这份试题也暗示和强调了向量和函数在解决数学问题中的工具性作用。

三是解答题第1题颠覆性地考查了导数，这是历年高考真题中从来没有出现的情况，近几年高考导数试题题号最靠前的就是2023年的新课标Ⅰ卷，放在第19题，其余基本都是放在最后两道题的位置。

四是解答题第4题圆锥曲线问题，如果用常规的方法来解答，虽然可以完成求解，但是计算量很大，学生要在有限的时间内按此方法得出正确结果难度非常大。但如果通过适当地添加辅助线，将三角形面积转化为四边形面积，就能很快计算出结果。

五是最后一题第19题，以新定义的方式出现，试题情境是在密码学理论中有重要地位的盖莫尔（ElGamal）加密体制，题干给了出离散对数的定义，要求考生利用该定义求解三个小问。其中第1小问较为容易，但第2、第3小问难度较大，要利用数论知识中的费马小定理进行求解。数论相关知识超出了普通高中数学教材必修和选择性必修的范畴。笔者翻阅了《普通高中数学课程标准（2017年版2020年修订）》（以下简称《课程标准》），发现它对“数论”的表述唯一一次出现的地方是在第四章“课程内容”中的第（三）部分“选修课程”中的“E类课程”即学校根据自身的需求开发或选用的课程，表述如下：“拓展视野的数学课程。例如，机器人与数学、对称与群、球面上的几何、欧拉公式与闭曲面分类、数列与差分、初等数论初步”［2］。本次九省联考出现这样一道题，确实令人匪夷所思，是否超出了《课程标准》的范畴也无法界定。但此题一出，一方面让极少部分的数学竞赛生感到惊喜，另一方面给了绝大多数的非数学竞赛生当头一棒。

六是从整卷的难度来看，一方面减少了题目数量，尤其是减少了1道较为耗时的多选题和1道解答题，从这点看，确实给了学生更多思考的时间；另一方面，除了各题型的最后一题，其他题目相对往年的联考题或高考真题，明显降低了难度，但填空题第14题和解答题第19题，明显带有浓厚的数学竞赛的味道，即便是解答题第18题，如果不采用巧妙的几何转化，计算也是非常困难。因此，这份联考试题在难度方面呈现出的一个特点便是常规问题更加简单，让大部分的学生能得到更多的分数，同时匀出更多时间让优秀的学生在更加灵活创新的题目上进行思考和比拼，目的是选拔出真正的拔尖创新型人才。

三、高考数学复习备考启示和建议

通过分析近年多省联考试题与当年高考新课标Ⅰ卷和Ⅱ卷的关联，以及分析2024年九省聯考试题发生的变化，笔者收获了一些启示，据此对高考数学复习备考提出如下建议。

（一）高度关注多省联考试题，及时适应试卷新结构

近年进行的两次多省联考的数学试题，与当年的高考新课标Ⅰ卷和Ⅱ卷的关联度还是相当高的，不仅题型结构和分值完全一致，而且各知识板块考查的占比和分值也非常接近。因此可以认为每年的多省联考在传递一些改革的信号，一定程度上指明了高考的方向，或者说在呈现一些命题的趋势。因此，在高考数学复习备考过程中，教师要高度重视对近年高考试题，尤其是对当年多省联考试题进行研究和分析，进而指导日常的复习备考教学。

2024年高考数学究竟会不会按新的试卷结构出题，笔者不敢妄自揣测，但是基于往年多省联考与当年高考试题高度关联，笔者强烈建议在往后的高考模拟题训练中，重视对新结构试题的训练，让学生提前熟悉试卷新结构，优化节奏把控、时间安排以及应试策略，提升学生面对试卷新结构的整体应对能力。

（二）重视主干知识，关注非主干知识的工具性

2024年的九省联考数学试题减少了题目的数量，这必然导致知识覆盖相对传统试题不够全面（例如向量、函数题的减少），因此在高三复习备考过程中，教师一方面要注重对主干知识的学习，重视理解和掌握主干内容的基础知识、基本技能、基本思想方法和基本学习路径；另一方面也要注重利用非主干知识（如集合、复数、向量、不等式、计数原理等）求解主干知识的过程，增强学生对非主干知识的工具性的体验和感受。

此外，九省联考试卷虽然减少了题目的数量，但除各题型的最后一题外，其余题目的难度较往年高考试题有了明显的降低，没有太偏、太难的问题，学生对常规问题的求解更加得心应手。命题者进行这样的难度设计，目的非常明确，就是希望大部分考生通过对基础知识、技能和思想方法的掌握，能够尽量多得分，而通过“题海战术”“机械刷题”等方式见识更多偏难怪题的学生将不占优势。也就是告诉所有考生，要抓住数学本质，而对大量刷题的行为，一定是耗时耗力却收效甚微的。

（三）重视训练解答创新性和探究性问题

2024年九省联考试题结构发生改变，一方面减少了题目数量，另一方面增加了各解答题的分值，并且在第14题、第18题、第19题明显加大了创新力度和解题难度。这样的设计可以看出命题者有以下几个非常明显的意图：一是减少题目数量，降低常规题难度，让大部分考生能够更快速地完成常规题目的解答，留下更多的时间思考求解难题和创新题；二是刻意调整知识板块在试卷中所处位置，打破高考试题固定、刻板的印象，增加创新性；三是解答题分值提高，更加注重考查数学思维，强调数学语言的严谨表达；四是常规问题求解时间减少，创新问题增加，以及第18题需进行几何转化，目的都是希望考生在数学测试中能够“少算多想”，通过最后几道解答题的比拼，真正选拔出具有较强数学思维能力和数学创新意识的人才，彰显《中国高考评价体系》中提到的高考“服务选才”的核心功能。

因此，笔者建议在高三数学复习备考中，一是更加注重对数学基础问题和本源问题的学习，强化对教材的学习和落实，减少机械刷题，追求“偏”“难”“怪”要及时“刹车”；二是让学生习惯各知识板块在不同位置考查的变化，以不变应万变；三是重视对创新性和探究性问题的训练和研究，培养学生的发散思维和对数学知识的迁移应用能力，充分体现数学问题的基础性、综合性、应用性和创新性特征。

最后，因为本次九省联考中第19题涉及了数论相关知识，是不是今后就要为学生补充数学竞赛相关知识？对此，笔者认为，参加过数学竞赛或其他学有余力的学生，可以适当拓展学习一些竞赛方面的内容，定期进行少量的竞赛知识补充和题目训练；而其他学生，扎实学好高中教材中的内容即可，没有必要再进行拓展延伸。

参考文献

［1］教育部考试中心.中国高考评价体系［M］.北京：人民教育出版社，2022.

［2］中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［M］.北京：人民教育出版社，2020.