一类非线性金融系统的多尺度效应研究

刘玲玉，李向红，王宏斌

（石家庄铁道大学a.数理系；b.经济管理学院，石家庄 050043）

0 引言

金融系统是家庭、公司和政府为执行其重要的金融决策而利用的一系列市场选择和中介。资金通过金融系统从盈余端流向短缺端，从而维持整个系统的稳定。但由于受到利率、投资等因素的影响，金融系统常常会变得非常复杂，甚至会出现失稳、失控等现象，从而影响经济的发展。因此，深入地分析和研究金融、经济系统的稳定性以及发展规律变得尤为重要，很多学者已经对一些金融、经济系统有了深入的研究，其中研究较多的是一类非线性金融系统。黄登仕和李后强（1993）[1]首次提出了这类由生产子块、货币子块、证券子块和劳动子块所组成的金融模型。Ma 和Chen（2001）[2]分析了这一模型的分岔混沌拓扑结构。Ma 等（2008）[3]在该金融系统中发现了奇异非混沌吸引子。Gao 和Ma（2009）[4]发现随着储蓄量的减小，该系统会从周期走向混沌。胡行华等（2018）[5]在经典金融模型的基础上提出了一个分数阶生物经济模型。

非线性金融系统是由生产、投资等要素组成的复杂系统，在实际运行过程中，会有许多不确定性因素存在，这就导致当某个变量发生微小变化时，可能会对其他变量造成很大的影响，从而导致多个变量在不同尺度上变化。已经有学者在经济系统中发现了多尺度问题以及簇发现象。Chian 等（2006）[6]用非线性经济周期的van der Pol 振子来模拟具有多尺度、混沌等特性的复杂经济系统。Krawiecki等（2002）[7]在微观金融市场模型中观察到价格序列表现为混沌簇发现象。事实上，多尺度问题还广泛存在于化学、机械等领域的系统中，很多学者对其进行了深入的研究。例如，Simo和Woafo（2011）[8]研究了机电系统中的簇发振荡；陈娅妮等（2020）[9]探究了一类含有两个慢变量的双稳态Duffing型系统中的簇发振荡现象。

综上所述，对于描述经济运行规律的各类系统，现有研究大多关注同一时间尺度上金融系统的稳定性、分岔、混沌等方面，对于多尺度耦合金融系统的快慢现象以及机理研究极少。本文将基于文献[1]提出的经典系统，考虑单位投资成本存在周期性微小扰动，经典非线性金融系统则具有两尺度耦合特征，形成一个快慢耦合非自治金融系统，并将快慢分析法[10]运用到此快慢耦合非线性金融系统中，挖掘其丰富的动力学行为，揭示经济运动规律的动力学机理，为金融系统的调控运行和决策提供理论支持。

1 数学模型

一类经典的非线性金融系统由文献[1]给出，如式（1）所示。

其中，变量x，y，z分别表示利率、投资需求、价格指数。a（≥0）为储蓄量，b（≥0）为单位投资成本，c（≥0）为商品需求弹性。

在经济运行过程中，投资处于非常重要的地位，它可能影响整个经济系统的动力学行为。例如，当失业率高或者经济相对落后时，各级政府会采取相关政策刺激投资，从而降低单位投资成本，提高就业率。而单位投资成本的降低也会增加投资需求，降低储蓄量。因此，单位投资成本的微小变化可能会影响整个金融系统的动力学行为。

假设系统（1）中单位投资成本存在弱周期扰动，它会导致单位投资成本的缓慢变化，模型为：

其中，b+εcos(ωt)在b-ε和b+ε之间变化，并且单位投资成本是非负的，因此b-ε≥0。

如果投资成本的扰动周期较长，即ω≤1 且与其他参数存在数量级上的差别，那么系统（2）包含两个时间尺度，基于快慢分析法[10]，系统可以被分成由x，y，z表示的快变过程以及由F=b+εcos(ωt)表示的慢变过程。快变过程可写为：

若将F考虑为一个参数，则系统（3）为自治系统，F的变化将导致系统（3）的稳定性发生变化，从而分岔行为会发生。系统（2）中，b+εcos(ωt)=F在[b-ε,b+ε]内缓慢周期性变化，这一慢变过程对系统（2）的动力学行为具有明显的调节作用，其本质是自治系统（3）的稳定性及其分岔等动力学行为影响了非自治系统（2）的振荡行为。因此下文将分析系统（3）的稳定性和分岔。

2 稳定性分析和分岔分析

为了求得系统（3）的平衡点，令系统（3）右端为0，可得：

求解方程（4）可得如下结果：

系统（3）的平衡点E0=(x0,y0,z0)可以分为两种情况：

在平衡点处，利率、投资需求、价格指数都保持不变。

基于文献[2]的稳定性分析结果，平衡点的稳定性如下：

（1）当c-F-acF≤0 且c+a-1/F＞0 时，系统有唯一渐近稳定的平衡点E01。

（2）当c-F-acF＞0 时,系统有三个平衡点E01，E02，E03，且有以下几种情况：

①平衡点E01为鞍点。

②当系统的参数满足Fc4+F2c3-2aF2c2+(2aF-2-3F2)c+3F=0 时，在平衡点E02,E03附近会产生Hopf分岔。

因此，随着参数的变化，该系统平衡点个数和稳定性都具有明显变化，存在典型的叉形分岔和Hopf 分岔特征。固定参数a=9.5，根据上述情况（2），结合平衡点E02,3的Hopf 分岔条件②，得到关于参数F和c的双参数分岔图，如图1所示。虚线下方为c-F-acF＞0 区域，其中，区域Ⅰ和区域Ⅲ为稳定区域，区域Ⅱ为不稳定区域。实线为Hopf分岔临界线，即当参数取到实线上时，系统（3）在平衡点E02,3附近发生Hopf分岔。

图1 系统（3）的双参数分岔图

平衡点的稳定性可以由特征根进行判别，平衡点E01处系统的Jacobi矩阵为：

则特征方程为：

平衡点E02,3处系统的Jacobi矩阵为：

则特征方程为：

为了详细描述系统的动力学行为，固定参数a=9.5，c=2.5。将参数代入方程（5）和方程（6）可得平衡点E01和E02,3的特征方程分别为：

下页图2（a）和图2（b）分别展示了系统（3）的平衡点E01和E02,3的特征值的实部和虚部随着参数F的变化情况。

图2 系统（3）平衡点的特征根实部和虚部

从图2（a）可以看出，对于平衡点E01来说，当0 ＜F＜0.101时，即在点状线左侧区域，有一个正实特征值和两个负实特征值，此时该平衡点为不稳定的鞍点；当F＞0.101时，三个特征值的实部均小于0，此时该平衡点渐近稳定。

从图2（b）可以看出，对于平衡点E02,3来说，当0 ＜F＜0.06 时，存在一个负实根和一对实部大于0的共轭复根，此时该平衡点为不稳定的焦点；当0.06 ＜F＜0.101 时，存在一个负实根和一对实部小于0的共轭复根，此时该平衡点为稳定焦点。取F=0.08，其时间历程图和相图如图3所示。

图3 F=0.08 时平衡点E02,3 为稳定焦点吸引子

依据以上分析，在参数a=9.5，c=2.5 的情况下，方程（3）关于慢变量F的分岔图如图4（a）所示。当参数F穿过点BP时，系统（3）的平衡点个数由一个变为三个，因此BP为叉形分岔点，并且叉形分岔参数临界值为FBP=0.101；根据前文中提到的Hopf 分岔发生的条件并代入参数可以求得FH1=FH2=0.06，因此稳定的极限环发生在0 ＜F＜0.06 范围内。图4（b）给出了F=0.05 时系统（3）存在的极限环，由于在Hopf 分岔临界点的左侧很快出现同时访问x正负半轴的大振幅极限环，因而此时Hopf 分岔为“鸭式爆炸”。

图4 系统（3）的分岔图和极限环

3 周期扰动下系统的动力学行为

令扰动频率ω=0.002，固定参数b=0.16，通过增大弱周期扰动幅值ε的值，不断扩大慢变量F的变化范围，整个系统（2）表现出从稳定到小振幅的簇发振荡，再到大振幅的混沌簇发振荡。

3.1 周期振荡

取ε=0.03，此时利率x和价格指数z都为0，投资需求y周期性变化，称之为周期振荡。此时整个系统处在相对稳定的一个状态。系统的时间历程图如图5所示。

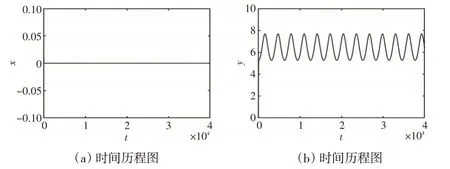
图5 b=0.16，ε=0.03 时系统（2）的周期振荡

3.2 BP型奇异非混沌簇发

增大ε的值为ε=0.10，系统出现典型的振荡行为，如图6（a）所示。图6（b）给出了Lyapunov指数图，实线、点状线和虚线分别代表三个Lyapunov指数。当时间足够长时，最大Lyapunov指数小于0，因此系统处于非混沌状态。从图6（c）可以看出，系统振荡形式具有“随机性”，因为系统会在x的正半轴和负半轴之间随机振动，因此该吸引子又称为奇异非混沌吸引子。此类系统存在“奇异非混沌吸引子”这种振动形式在文献[3,4]中也有提及。

图6 b=0.16，ε=0.10 时系统（2）的簇发振荡

此外，整个系统也表现为典型的簇发振荡行为，因为具有典型的相对大幅振荡的SP（激发态）和小振幅振荡的QS（沉寂态）的耦合，其时间历程图如图6（c）所示。其中，SP 指向的小图为激发态的局部放大图，可以看到呈现相对大幅振荡的状态。

为了揭示簇发振荡的机理，首先给出系统变量x和慢变过程F=0.16+0.10 cos(0.002t) 的转换相图（见下页图7）。由时间历程图6（c）可以看出，系统会随机访问x正半轴和负半轴，因此将转换相图按照时间和方向进行分解，并将其和分岔图（图4（a））叠加。下页图8 表示轨线运行方式是从上半支出发，从上半支返回；下页图9 表示从下半支出发，从下半支返回。这两种运动模式分别简称为上上行、下下行。

图7 b=0.16，ε=0.10 时系统（2）的转换相图

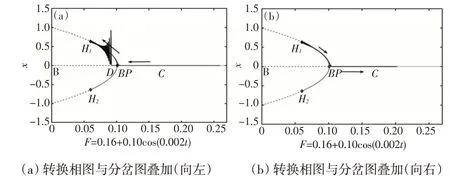
图8 b=0.16，ε=0.10 时系统（2）的簇发振荡机制（从上半支出发，从上半支返回）

图9 b=0.16，ε=0.10 时系统（2）的簇发振荡机制（从下半支出发，从下半支返回）

由于图8 和图9 两种运动模式虽然运动方向不同，但是振荡机理相近，因此不妨以图8为例详细描述整个簇发振荡的演变过程。不妨假设系统从C点出发，由于C点处于稳定的平衡线上，则将从C点向左运动，这时系统处于沉寂态。直到遇到叉形分岔点BP，这里有一个微小的时滞到达D点，由于稳定焦点的吸引，系统会发生微小高频振荡，形成激发态。由于稳定焦点的吸引使得激发态的振幅逐渐变小，最终收敛到上半支稳定的平衡线上，即激发态变为沉寂态。当轨线到达最左端H1点时，慢变过程F=0.16+0.10 cos(0.002t)达到最小值。接下来，轨线将调转方向，按照F增大的方向运动，如图8（b）所示，此时系统一直沿着稳定平衡线向右运动，保持沉寂态，直到F=0.16+0.10 cos(0.002t)到达最大值点。接着，轨线又按照F减小的方向运动，直到遇到叉形分岔点BP，此时系统会随机地访问上半支和下半支，即随机地按照图8或者图9的情形运动，如此往复。系统（3）的BP分岔导致系统（2）轨线向左运行访问上、下两支稳定平衡线具有不确定性，但是其Lyapunov指数都是非正的，因此称之为BP型奇异非混沌簇发。

3.3 BP-Hopf型混沌簇发

继续增大ε为ε=0.16，相图如图10（a）所示，此时振荡呈现明显的混沌特征。其Lyapunov 指数如图10（b）所示，实线、点状线和虚线分别代表三个Lyapunov 指数。当时间足够长时，最大Lyapunov 指数大于0，因此整个金融系统处于混沌状态。

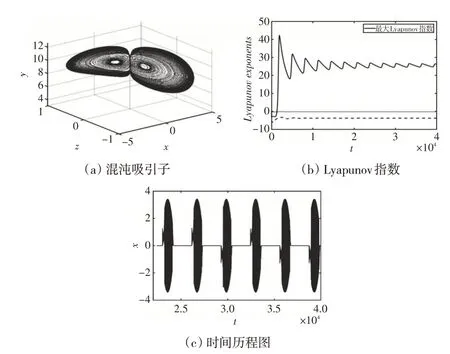
图10 b=0.16，ε=0.16 时系统（2）的簇发振荡

整个系统处于典型的簇发振荡中，其时间历程图如图10（c）所示。整个振荡过程依然是大幅振荡的SP（激发态）和小振幅振荡的QS（沉寂态）的耦合，但激发态特征更加明显。

从图10（c）中可以看出，系统会随机地访问上半支或者下半支，形成四种运动形式，并形成SP 和QS 之间的切换。为了揭示簇发振荡的机理，给出快变量x和慢变过程F=0.16+0.10 cos(0.002t)的转换相图，如图11所示。将转换相图按照时间和方向进行分解并和分岔图（图4（a））叠加，图12表示从上半支出发，从下半支返回；下页图13表示从下半支出发，从上半支返回。从上半支出发，从上半支返回的情形是图12（a）与图13（b）的结合；从下半支出发，从下半支返回的情形是图13（a）与图12（b）的结合。这四种运动模式分别简称为上下行、下上行、上上行、下下行。

图12 b=0.16，ε=0.16 时系统（2）的簇发振荡机制（从上半支出发，从下半支返回）

图13 b=0.16，ε=0.16 时系统（2）的簇发振荡机制（从下半支出发，从上半支返回）

由于四种运动模式虽然运动方向不同，但是振荡机理相近，因此以图12 为例详细描述整个簇发振荡的演变过程。不妨假设系统从C点出发，由于C点处于稳定的平衡线上，因此将从C点向左运动，这时系统处于沉寂态。直到遇到叉形分岔点BP，由于稳定焦点的吸引到达D点，系统会发生微幅高频振动，稳定焦点的吸引会使得振幅逐渐减小，这一过程很短暂，因为到达Hopf 分岔点H1后，由于受到稳定极限环的影响，系统会又呈现大幅振荡的激发态，即区域Ⅰ的大幅振荡，这种大幅振荡一直持续到慢变过程F=0.16+0.16 cos(0.002t) 达到最小值。接下来，轨线将调转方向，按照F增大的方向运动，即图12（b），由于处于稳定的极限环区域，系统将会继续大幅振荡，这种同时访问上、下坐标轴的大幅振动一直持续到Hopf 分岔点。超过H1,2后，轨线受到x轴下方稳定平衡点的吸引，振幅逐渐变小，越过叉形分岔点BP后，逐渐收敛到平衡线上，直到到达F的最大值点，轨线又按照F减小的方向运动，直到遇到叉形分岔点BP，此时轨线将会随机访问上、下分支，即随机地按照上下行、下上行、上上行、下下行的情形运动，如此往复。由于系统在振动过程中与BP叉形分岔和Hopf 分岔密切相关，因此称之为BP-Hopf混沌簇发。

与BP 型奇异非混沌簇发相比，BP-Hopf 混沌簇发具有两种明显的特征：一是激发态突出；二是随机性也更加明显。事实上，激发态突出是因为此时系统（2）的轨线在运行过程中不仅会遇到系统（3）的稳定焦点导致的小幅振动，还会受到系统（3）“鸭式爆炸”产生的大幅极限环的吸引，从而出现大幅高频振动，因而激发态凸显。另外，BP分岔导致系统（2）向左运行时存在随机访问x上、下半轴的情形；同时，访问上、下半轴的大幅极限环又使得系统（2）向右运行越过Hopf分岔后也出现了随机访问x上、下半轴的情形，因此导致了四种运行方式。随机性更加突出，这也最终导致了混沌的出现。

综上三种情形，可以发现大致描述了金融系统的一个调节过程。当ε=0.03 时，利率x为0，没有簇发现象，整个系统处于相对稳定的状态。但零利率一般出现于经济低迷期，此时可以通过降低利率以增加投资的方式，提高资金的流动来带动经济的发展，因此到了第二种情况，即增大ε=0.10，由于周期扰动的存在，系统会出现小振幅的簇发振荡，利率会在一个相对小的振幅范围内波动，降低到一定程度，然后利率开始增加，循环往复维持系统的运行。当扰动更大时，即第三种情况ε=0.16，系统会发生比较剧烈的混沌簇发振荡，整个金融系统处于典型的混沌状态。因此，政府部门又会降低投资来使经济降温，平稳回落，如此往复维持金融系统的正常运转。

4 周期扰动幅值对簇发振荡的影响

由系统（3）的分岔图（图4（a））可知，Hopf分岔点的参数临界值为FH1=FH2=0.06。这就说明，当F＜0.06 时，系统（3）存在稳定的极限环吸引子；当F＞0.06 时，系统（3）存在稳定的极限环与稳定焦点吸引子。当激励幅值范围的两个端点值满足b-ε＜0.06 ＜b+ε时，F在b-ε和b+ε之间变化，整个系统会涉及两种吸引子，稳定的极限环和稳定焦点吸引子使得整个系统在激发态和沉寂态之间跃迁，导致了簇发振荡的产生，见图11；当幅值范围满足0.06 ＜b-ε时，整个系统涉及稳定焦点吸引子，出现小幅振荡与沉寂态的跃迁状态，见图7；当幅值范围满足0 ＜b-ε＜b+ε＜0.06 时，整个系统只涉及极限环吸引子，从而只呈现大幅振荡状态，沉寂态消失，见图14。

因此，当b和ω一定时，扰动幅值ε决定了慢变过程F=b+εcos(ωt)的变化范围，调节着整个系统（2）涉及快变过程（3）的吸引子类型，进而影响了簇发振荡的诱导机理，从而影响了整个金融系统的运行状态。

5 结论

金融系统是一个复杂系统，相关因素较多。投资是金融系统中非常重要的一个元素，是经济发展的推动力。因此，考虑将周期微小扰动加入投资项中，整个系统将会是一个快慢耦合非自治系统，并且该系统在一定参数范围内存在复杂的奇异非混沌簇发和混沌簇发振荡。本文研究发现，这一快慢耦合非自治金融系统与其相应的自治系统具有密切关系，自治系统存在的各种分岔和吸引子对非自治系统的振荡行为具有明显的调节作用。自治系统的叉形分岔和稳定焦点吸引子导致了非自治系统的BP型奇异非混沌簇发振荡；自治系统的叉形分岔、Hopf分岔、稳定焦点吸引子和稳定极限环吸引子是非自治系统的BP-Hopf型混沌簇发振荡的产生机理。自治系统分岔时对称吸引子的出现使得非自治系统访问对称吸引子出现“随机性”。本文还发现，当扰动幅值处于很小的范围内时，系统无簇发现象发生；随着幅值范围扩大，系统涉及叉形分岔，由于受到不同焦点吸引子的吸引，因此系统在沉寂态和激发态之间切换；当幅值范围进一步增大时，系统会出现叉形分岔和Hopf 分岔，极限环吸引子的出现会使得系统激发态更加明显。

综上所述，当单位投资成本发生微小变化时，可能会对经济运行产生较大影响。因此，在实际经济运行过程中，合理控制投资成本的变动范围才能保证经济相对平稳地运行。本文基于快慢分析理论给出了系统的具体振荡模态，并进行深入的诱导机理解释，这为实际的经济运行提供了可操作的方法。