重构学习单元，创新学习指导

王银

在新教材、新课程、新高考的“三新”背景下，立体几何中空间几何体模块知识的高考命题与综合应用更加新颖创新，特别是有关空间几何体截面知识的应用，成为高考数学命题的一个热点与亮点，备受各方关注.涉及空间几何体的截面问题，源于高中教材，依托教材合理构建截面概念；在此基础上，强化截面的本质与内涵，增加平面几何与立体几何等相关知识之间的联系；彰显与截面相关知识的应用，充分体现数学意识与数学思维能力；强化截面的数学应用，着力应用意识与创新意识等.此类问题成为高考数学命题中既充分体现知识基础，又体现选拔功能的一类创新考点.

1依托教材，构建概念

“三新”背景下空间几何体的截面的命题，回归高中数学教材，突出对空间几何体的结构特征、截面的概念与形状等层面的考查，注重空间想象能力与直观想象素养等，合理构建对应的概念与相关的知识网络，注重对空间几何体的基础知识的理解与掌握，全面夯实基础.

例1（人教A版必修第二册例3）如图1所示的一块木料中，棱BC平行于面A′C′.

（1）要经过面A′C′内的一点P和棱BC将木料锯开，在木料表面应该样画线？

（2）所画的线与平面AC是什么位置关系？

具体的分析与解析过程可以参考教材中的对应部分（教材第138页），这里不再展开.初步总结并提炼空间几何体中截面问题的解答策略，体会空间中点、线、面的“动”与“静”之间的联系，领悟“平面”与“立体”之间的化归与转化思想.在此基础上，给出空间几何体中截面的概念.

截面：用一个平面去截一个空间几何体（经过空间几何体内部的点），得到的平面图形叫做这个空间几何体的截面（其中，截面与空间几何體表面的交线叫做截线）.

特别地，经过空间几何体的内部，且每条边都在空间几何体表面上的封闭图形，可以作为空间几何体的截面.

基于此，可以通过截面的作法与确定来强化本质，加强平面几何与立体几何之间的联系；借助截面的形状判断来彰显能力，凸显空间想象思维、分类讨论思想以及化归与转化思想等；结合截面图形的面积或周长等来着力创新，强化数学的应用意识与创新意识等.

2强化本质，增加联系

“三新”背景下空间几何体的截面的命题，基于空间几何体的截面的概念、空间几何体的结构特征等，以及问题的场景应用等，合理综合立体几何中点、线、面的位置关系等，合理通过截面的作法与确定，强化截面的本质，从而构建立体几何与平面几何等相关知识之间的联系.

例2正方体ABCD-A1B1C1D1中，已知点E，F，G分别在棱AB，BC，DD1上，如图2所示，求作过E，F，G三点的截面.

正方体的截面，是空间几何体的截面问题中最常见的基本类型之一.从题设条件入手，抓住正方体的结构特征加以合理分析与确定，巧妙联系起立体几何与平面几何之间的关系与应用等.

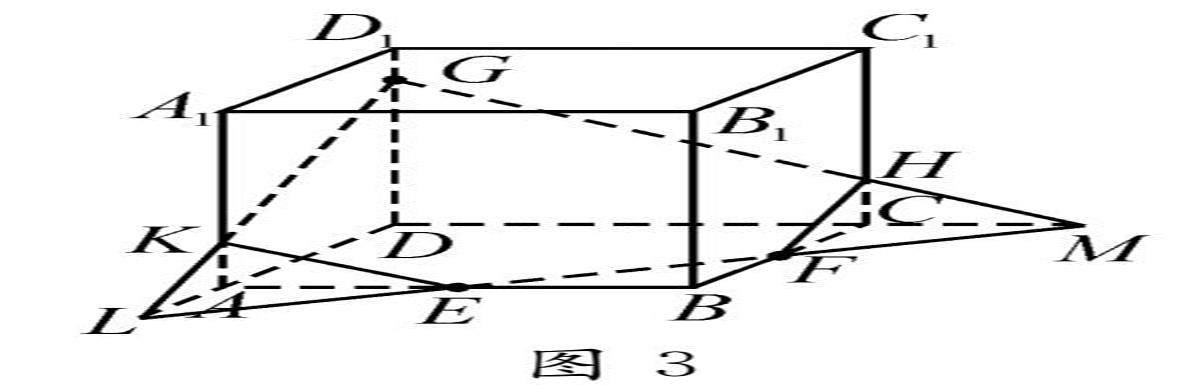
图3

作法：如图3，（1）在正方体ABCD-A1B1C1D1的底面ABCD内，过E，F两点作出直线EF，该直线分别与棱DA，DC的延长线交于点L，M；

（2）在正方体的侧面AA1D1D内，连接LG，并交棱AA1于点K；在正方体的侧面DD1C1C内，连接GM，并交棱CC1于点H；

（3）连接KE，FH，则五边形EFHGK即为所求的过E，F，G三点的截面.

归纳起来，正方体的截面主要有以下几种情况：正方体的横截面为正方形；纵截面为正方形或矩形；斜截面的情况如图4.

在解决空间几何体的截面作法或与之有关的判断问题时，要强化直观想象意识以及空间想象能力等，借助立体几何图形，从立体到平面进行降维处理，有时还要涉及数形结合思想以及化归转化思想等.

3彰显能力，凸显思维

“三新”背景下空间几何体的截面的命题，在截面的作法与确定的基础上，合理判断并确定截面的形状等应用，彰显能力，突出对空间几何体的结构特征以及题设条件的应用，突出立体几何与平面几何等相关知识之间的联系，以及图形结构特征的内涵与本质等，凸显数学思维.

例3（多选题）如图5，已知正方体ABCD-A1B1C1D1的棱长为1，其中P为BC的中点，Q为线段CC1上的一个动点，设CQ=m，若过A，P，Q三点的截面记为S.则下列命题中正确的是（）.（答案：ABC.）

A.当0

B.当m=12时，截面S为等腰梯形

C.当m=34时，截面S与棱C1D1的交点R满足C1R=13

D.当34

在解决有关立体几何中的截面形状判断以及与截面的几何性质相关的应用问题时，要合理综合运用立体几何中相关的基本性质，综合平面几何的基本性质，并结合直观想象与空间想象来分析与处理.

4着力创新，强化应用

“三新”背景下空间几何体的截面的命题，合理创设问题场景，利用动点、动直线、动平面等合理“动态”引入，以截面图形的面积或周长等的确定或对应最值的判断等来着力创新，强化空间几何体的综合应用，特别有时要联系起函数与方程、不等式、三角函数与解三角形、平面解析几何等知识的交汇与应用.

例4已知正四面体ABCD的棱长为2，平面α与棱AB，CD均平行，则平面α截该正四面体所得截面面积的最大值为（）.

A.1

B.2

C.3

D.2

图6

解析：如图6，取CD的中点O，连接OA，OB.因为△ACD为等边三角形，O为CD的中点，所以OA⊥CD.同理OB⊥CD.

又OA∩OB=O，所以CD⊥平面AOB，又AB平面AOB，所以CD⊥AB.

设平面α分别交AC，AD，BD，BC于点E，F，G，H，连接EF，FG，GH，HE.

因为CD∥平面α，CD平面ACD，平面ACD∩平面α=EF，

所以CD∥EF.同理GH∥CD，EH∥AB，FG∥AB.

所以EF∥GH，EH∥FG，故EFGH为平行四边形.

又AB⊥CD，则EF⊥EH，所以EFGH为矩形.

设AEAC=x（0

因为EF∥CD，所以EFCD=AEAC=x，于是EF=2x，同理可得EH=2（1－x）.

所以矩形EFGH的面积S=EF·EH=2x·2（1－x）≤4x+1－x22=1，当且仅当x=12时，等号成立，即平面α截该正四面体所得截面面积的最大值为1.故选：A.

解决截面面积最值问题的方法与技巧主要是：首先根据几何体的结构特征以及截面所在平面满足的条件，确定截面的形状，然后合理设置变量，用变量表示出截面面积，最后利用均值不等式或函数的性质求出最值，即可求得截面面积的最值.

在新教材、新课程、新高考的“三新”背景下，进一步落实“双减”政策与新课改理念，探寻立体几何中考点与考题的基础性、应用性与创新性等，基于“四基”的落实与数学能力的提升，更加注意创新意识与创新应用，从而指向数学核心素养的培养.

课题信息：江苏省教育科学“十四五”规划重点课题“学习进阶理论下高中数学单元学习元指导研究”，课题编号为B/2022/03/65.