借助思维导图将思维“可视化”，探寻解题轨迹

杨东 陈霞 邹蕴博 陈洲健

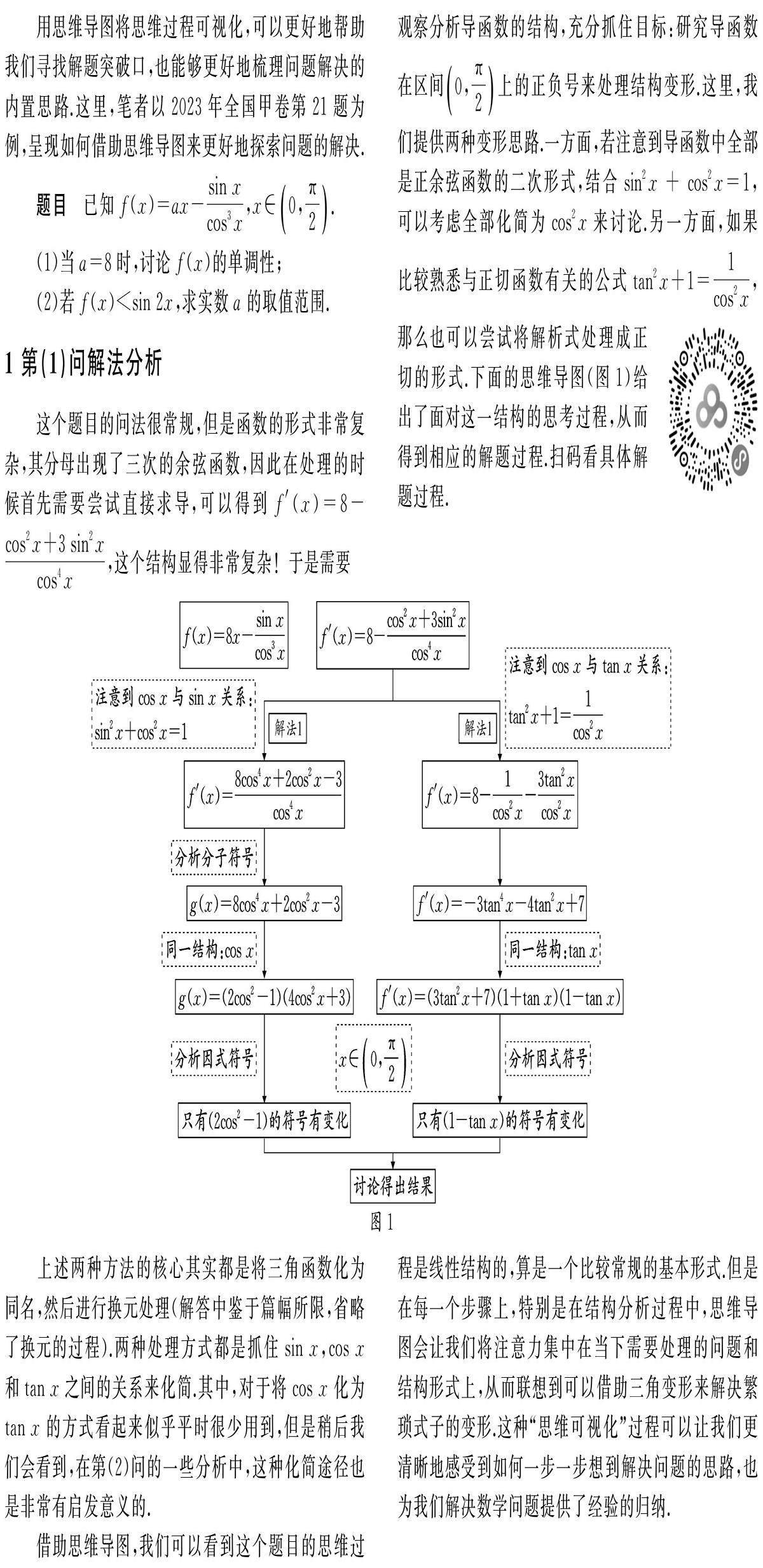
用思维导图将思维过程可视化，可以更好地帮助我们寻找解题突破口，也能够更好地梳理问题解决的内置思路.这里，笔者以2023年全国甲卷第21题为例，呈现如何借助思维导图来更好地探索问题的解决.

题目 已知f（x）=ax－ sin x cos3x ，x∈ 0， π 2  .

（1）当a=8时，讨论f（x）的单调性；

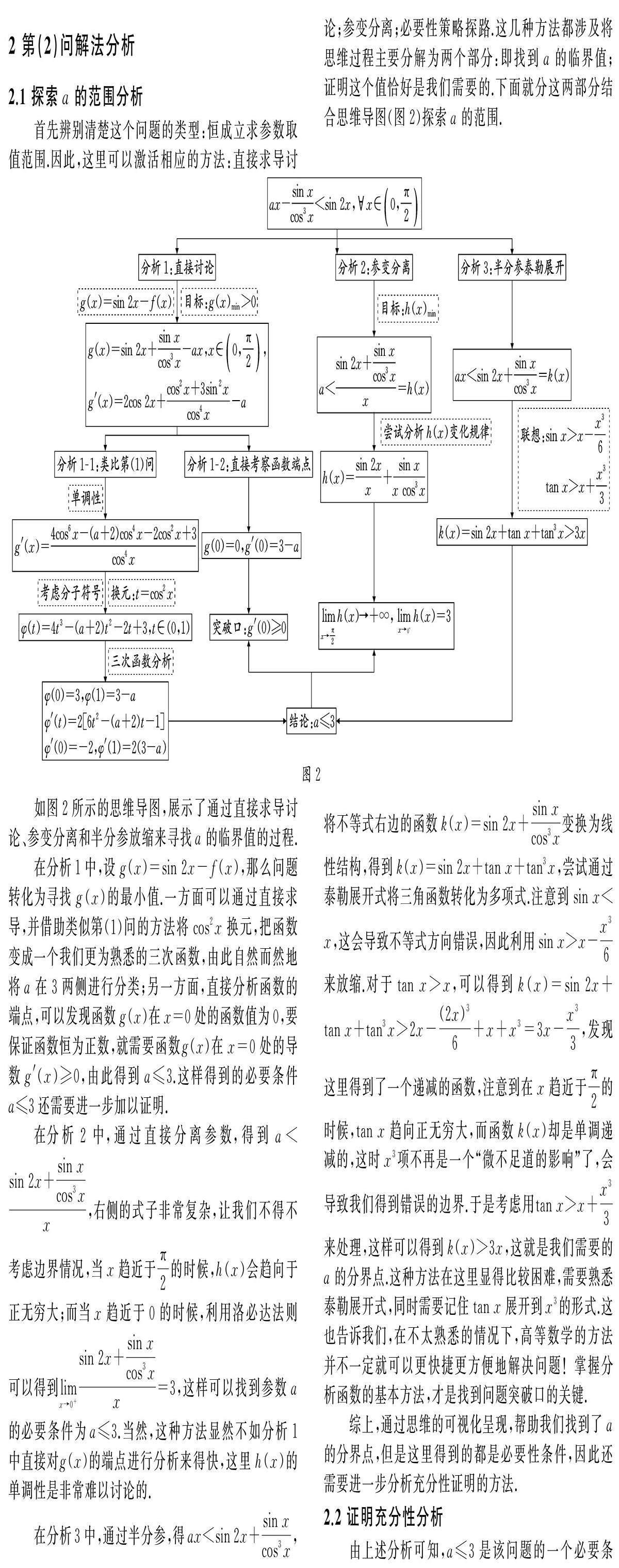
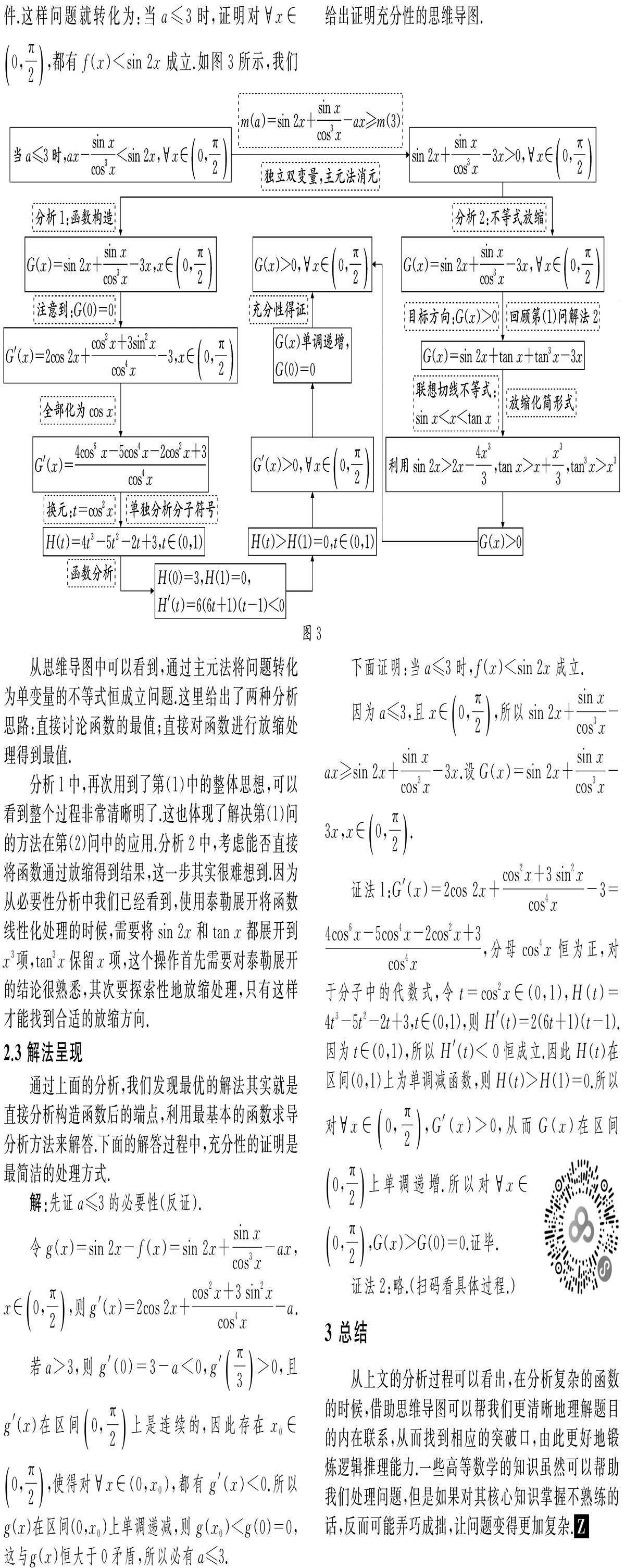
（2）若f（x）

1 第（1）问解法分析

这个题目的问法很常规，但是函数的形式非常复杂，其分母出现了三次的余弦函数，因此在处理的时候首先需要尝试直接求导，可以得到f′（x）=8－ cos2x+3sin2x cos4x ，这个结构显得非常复杂！于是需要观察分析导函数的结构，充分抓住目标：研究导函数在区间 0， π 2  上的正负号来处理结构变形.这里，我们提供两种变形思路.一方面，若注意到导函数中全部是正余弦函数的二次形式，[JP+1]结合sin2x + cos2x=1，可以考虑全部化简为cos2x来讨论.另一方面，如果比较熟悉与正切函数有关的公式tan2x+1= 1 cos2x ，

那么也可以尝试将解析式处理成正切的形式.

下面的思维导图（图1）给出了面对这一结构的思考过程，从而得到相应的解题过程.扫码看具体解题过程.

上述两种方法的核心其实都是将三角函数化为同名，然后进行换元处理（解答中鉴于篇幅所限，省略了换元的过程）.两种处理方式都是抓住sin x，cos x和tan x之间的关系来化简.其中，对于将cos x化为tan x的方式看起来似乎平时很少用到，但是稍后我们会看到，在第（2）问的一些分析中，这种化简途径也是非常有启发意义的.

借助思维导图，我们可以看到这个题目的思维过程是线性结构的，算是一个比较常规的基本形式.但是在每一个步骤上，特别是在结构分析过程中，思维导图会让我们将注意力集中在当下需要处理的问题和结构形式上，从而联想到可以借助三角变形来解决繁琐式子的变形.这种“思维可视化”过程可以让我们更清晰地感受到如何一步一步想到解决问题的思路，也为我们解决数学问题提供了经验的归纳.

2 第（2）问解法分析

2.1 探索a的范围分析

首先辨别清楚这个问题的类型：恒成立求参数取值范围.因此，这里可以激活相应的方法：直接求导讨论；参变分离；必要性策略探路.这几种方法都涉及将思维过程主要分解为两个部分：即找到a的临界值；证明这个值恰好是我们需要的.下面就分这两部分结合思维导图（图2）探索a的范围.

如图2所示的思维导图，展示了通过直接求导讨论、参变分离和半分参放缩来寻找a的临界值的过程.

在分析1中，设g（x）=sin 2x-f（x），那么问题转化为寻找g（x）的最小值.一方面可以通过直接求导，并借助类似第（1）问的方法将cos2x换元，把函数变成一个我们更为熟悉的三次函数，由此自然而然地将a在3两侧进行分类；另一方面，直接分析函数的端点，可以发现函数g（x）在x=0处的函数值为0，要保证函数恒为正数，就需要函数g（x）在x=0处的导数g′（x）≥0，由此得到a≤3.这样得到的必要条件a≤3还需要进一步加以证明.

在分析2中，通过直接分离参数，得到a< sin 2x+ sin x cos3x  x ，右侧的式子非常复杂，让我们不得不考虑边界情况，当x趋近于 π 2 的时候，h（x）会趋向于正无穷大；而当x趋近于0的时候，利用洛必达法则可以得到lim x→0+  sin 2x+ sin x cos3x  x =3，这样可以找到参数a的必要条件为a≤3.当然，这种方法显然不如分析1中直接对g（x）的端点进行分析来得快，这里h（x）的单调性是非常难以讨论的.

在分析3中，通过半分参，得axx－ x3 6 来放缩.对于tan x>x，可以得到k（x）=sin 2x+tan x+tan3x>2x－ （2x）3 6 +x+x3=3x－ x3 3 ，发现这里得到了一个递减的函数，注意到在x趋近于 π 2 的时候，tan x趋向正无穷大，而函数k（x）却是单调递减的，这时x3项不再是一个“微不足道的影响”了，会导致我们得到错误的边界.于是考虑用tan x>x+ x3 3 来处理，这样可以得到k（x）>3x，这就是我们需要的a的分界点.这种方法在这里显得比较困难，需要熟悉泰勒展开式，同时需要记住tan x展开到x3的形式.这也告诉我们，在不太熟悉的情况下，高等数学的方法并不一定就可以更快捷更方便地解决问题！掌握分析函数的基本方法，才是找到问题突破口的关键.

综上，通过思维的可视化呈现，帮助我们找到了a的分界点，但是这里得到的都是必要性条件，因此还需要进一步分析充分性证明的方法.

2.2 证明充分性分析

由上述分析可知，a≤3是该问题的一个必要条件.这样问题就转化为：当a≤3时，证明对x∈ 0， π 2  ，都有f（x）

从思维导图中可以看到，通过主元法将问题转化为单变量的不等式恒成立问题.这里给出了两种分析思路：直接讨论函数的最值；直接对函数进行放缩处理得到最值.

分析1中，再次用到了第（1）中的整體思想，可以看到整个过程非常清晰明了.这也体现了解决第（1）问的方法在第（2）问中的应用.分析2中，考虑能否直接将函数通过放缩得到结果，这一步其实很难想到.因为从必要性分析中我们已经看到，使用泰勒展开将函数线性化处理的时候，需要将sin 2x和tan x都展开到x3项，tan3x保留x项，这个操作首先需要对泰勒展开的结论很熟悉，其次要探索性地放缩处理，只有这样才能找到合适的放缩方向.

2.3 解法呈现

通过上面的分析，我们发现最优的解法其实就是直接分析构造函数后的端点，利用最基本的函数求导分析方法来解答.下面的解答过程中，充分性的证明是最简洁的处理方式.

解：先证a≤3的必要性（反证）.

令g（x）=sin 2x－f（x）=sin 2x+ sin x cos3x －ax，x∈ 0， π 2  ，则g′（x）=2cos 2x+ cos2x+3sin2x cos4x －a.

若a>3，则g′（0）=3－a<0，g′ [SX（]π[]3[SX）] ＞0，

且g′（x）在区间 0， π 2  上是连续的，因此存在x0∈ 0， π 2  ，使得对x∈（0，x0），都有g′（x）<0.所以g（x）在区间（0，x0）上单调递减，则g（x0）

下面证明：当a≤3时，f（x）

因为a≤3，且x∈ 0， π 2  ，所以sin 2x+ sin x cos3x －ax≥sin 2x+ sin x cos3x －3x.设G（x）=sin 2x+ sin x cos3x －3x，x∈ 0， π 2  .

证法1：G′（x）=2cos 2x+ cos2x+3sin2x cos4x －3= 4cos6x－5cos4x－2cos2x+3 cos4x ，分母cos4x恒为正，对于分子中的代数式，令t=cos2x∈（0，1），H（t）=4t3－5t2－2t+3，t∈（0，1），则H′（t）=2（6t+1）（t－1）.因为t∈（0，1），所以H′（t）< 0恒成立.因此H（t）在区间（0，1）上为单调减函数，则H（t）>H（1）=0.所以对x∈ 0， π 2  ，G′（x）＞0，从而G（x）在区间 0， π 2  上单调递增.所以对?x∈ 0， π 2  ，G（x）>G（0）=0.证毕.

证法2：略.（扫码看具体过程.）

3 总结

从上文的分析过程可以看出，在分析复杂的函数的时候，借助思维导图可以帮我们更清晰地理解题目的内在联系，从而找到相应的突破口，由此更好地锻炼逻辑推理能力.一些高等数学的知识虽然可以帮助我们处理问题，但是如果对其核心知识掌握不熟练的话，反而可能弄巧成拙，让问题变得更加复杂.