基于云模型和改进D-S证据理论的浓香型白酒发酵质量评估方法
陈 博, 杨亭榆, 刘艾萌, 赖冬寅
(四川工商职业技术学院智能制造与信息工程学院, 四川 都江堰 611830)
浓香型白酒是一种以粮谷为原料,浓香大曲为糖化发酵剂,经泥窖固态发酵后,固态蒸馏、陈酿、勾调而成[1]。浓香型白酒的发酵过程是一个厌氧生物发酵的过程,采用封闭式的固态发酵,发酵中途无法通过检测发酵参数分析准确评估发酵状态[2]。虽然酒醅参数最能反映发酵整体质量,但是酒醅作为半固体的形态,对于它的理化参数的检测,首先需要对黄水进行繁杂的样品前处理,速度较慢。而黄水作为浓香型白酒发酵过程中最重要的副产物,在较大程度上能够反映发酵质量[3]。因此通过快速检测黄水液体理化参数,用于发酵质量的评估分析,并进一步指导浓香型白酒生产工艺,包括蒸馏和黄水的回收利用,从而提高浓香型白酒的生产效率。
目前对于发酵质量的评估主要依赖人工经验进行判断。首先需要将定量的参数转化为对于发酵质量定性的描述。而云模型是一种描述定性概念与定量描述之间不确定转换的数学模型,同时集成模糊性和随机性[4]。程方明等[5]通过建立云模型作为评价模型,结合序关系分析法和熵权法确定权重,分析了某变电站火灾风险等级。刘纪坤等[6]采用改进的层次分析法(analytic hierarchy process,AHP)-熵权组合赋权法来分配权重,结合云模型理论技术,综合分析了某地铁站应急能力。通过云模型将测得定量的黄水理化参数映射成发酵质量的定性描述,保留了评价过程的随机性和模糊性。
黄水理化参数包含酸度、还原糖以及酒精度等,它们对于发酵质量的判断结果可能不一致甚至存在冲突。D-S(Dempster-Shafer)证据理论是一种解决多种数据融合的方法,被广泛应用于决策融合和信息融合方面[7]。闫善勇[8]提出了一种基于D-S证据理论的关联方法,利用Dempster规则对证据进行组合,采用Murphy方法处理证据冲突,实现雷达目标与敌我识别(identification friend or foe,IFF) 点迹的有效关联。张欢等[9]针对传统D-S证据理论所存在的证据冲突问题,利用皮尔逊相关系数对证据的权重进行修正,提出了一种改进的D-S证据理论。本文采用D-S证据理论将不同黄水参数的判断结果进行融合,针对证据间的冲突,提出了一种基于改进冲突系数的D-S证据理论,有效地降低冲突焦元的影响以及融合结果中的不确定性部分的概率分布。
1 黄水参数云模型
云模型广泛应用于定性概念与定量表达之间的相互转化,将概率论和模糊集合论进行融合,可以更好地体现出概念的不确定性,广泛应用于工程领域。不确定性是相对精度的概念,包含模糊性与随机性,模糊性主要指任主观理解上的不确定性,而随机性反映的是自然规律的不确定性[10]。云模型数字特征由期望值Ex、熵En和超熵He这3个值表示,它把模糊性和随机性完全集合在一起,构成定性和定量之间的映射作为知识表示的基础[11]。其中,Ex是云滴的分布期望,也是这个概念最典型的量化样本,它反映了云滴群分布的平均位置;熵En是定性概念不确定性的度量,包括随机性和模糊性,随机性是指能反映这一概念的云滴的离散性,模糊性是指在论域中能反映概念的云滴取值范围;超熵He是En的不确定性的度量,即熵的熵,超熵越小,代表云滴分布越紧密,越大代表云滴分布越离散。
浓香型白酒的发酵过程的本质是一个从淀粉到葡萄糖、到乙醇、再到各种香味成分的过程,发酵产物中的各个参数的高低可以反映这个过程进行得是否充分[12]。目前对于发酵状态和发酵质量主要是基于人工经验,通过酒醅温度、气味、水分进行综合判断,具体一定程度的主观性和不稳定性。酒醅的理化检测数据虽然可以准确检测出发酵产物中的醇类、酸类、酯类物质成分,但由于样品前处理复杂,检测结果相比实际生产具有滞后性,无法及时用于指导生产。而黄水作为浓香型白酒的发酵副产物,在发酵中后期,各类醇类、酸类物质以及其他发酵产物会沉降到黄水中,通过分析黄水参数可判断发酵质量。根据某酒厂黄水参数与实际生产数据(出酒率、总酸、总酯等)的关联分析,整合得到表1中的黄水对发酵质量的评价标准,表中分别反映了黄水酸度、还原糖和酒精度3大成分,在不同区间时,对于发酵质量的定性评价,包含优、中、差3个等级。

表1 黄水对发酵质量的评价标准
基于表1中的发酵质量分布,可以得到不同参数对于发酵质量进行定性评价云模型的参数期望Ex;结合其他定性评价的参数期望,可以得到熵En;选择合适的超熵He,并通过MATLAB绘制云图。最终可以对黄水的酸度、还原糖酒精度3个参数对于发酵质量的映射概率分布建立相应云模型,如图1所示。对于黄水样本,可以根据它的酸度、还原糖、酒精度分别在图中得到对于发酵质量判断结果的概率分布,其中不满1的部分算作不确定概率m(X)。

图1 黄水酸度、还原糖、酒精度隶属度云模型
2 基于黄水参数的发酵质量定量分析
黄水样品通过理化测定方式,分别测量出各自的酸度(以酚酞为指示剂用0.1 mol/L氢氧化钠标准溶液滴定)、还原糖(碱性酒石酸铜甲液和乙液在加热状态下滴定)和酒精度(酒精计测量)的生产数据[13-15]。为验证黄水参数对于发酵的参考性,在采集黄水样品时也整合了酒厂的相关生产数据,包括基酒产量、酒醅总酸及酒醅总酯,5个样本的生产数据见表2。再通过各样本的黄水参数的隶属度模型得到对于样本在该参数上“优”“中”“差”的分布概率m(A3)、m(A2)、m(A1),除去这3种分布以外的余量采用不确定m(X)来表示,以满足D-S证据理论归一化的运算前提。最终黄水样本各参数对应的概率分布见表3。
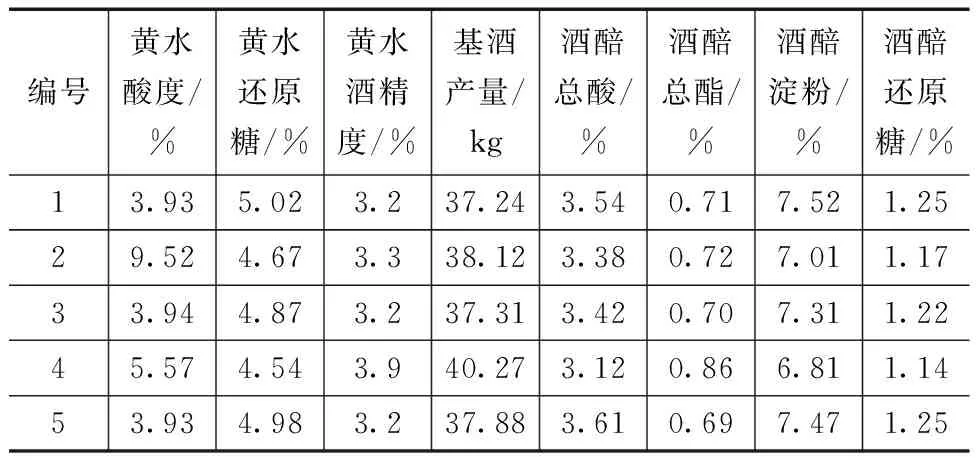
表2 黄水样本的相关生产数据
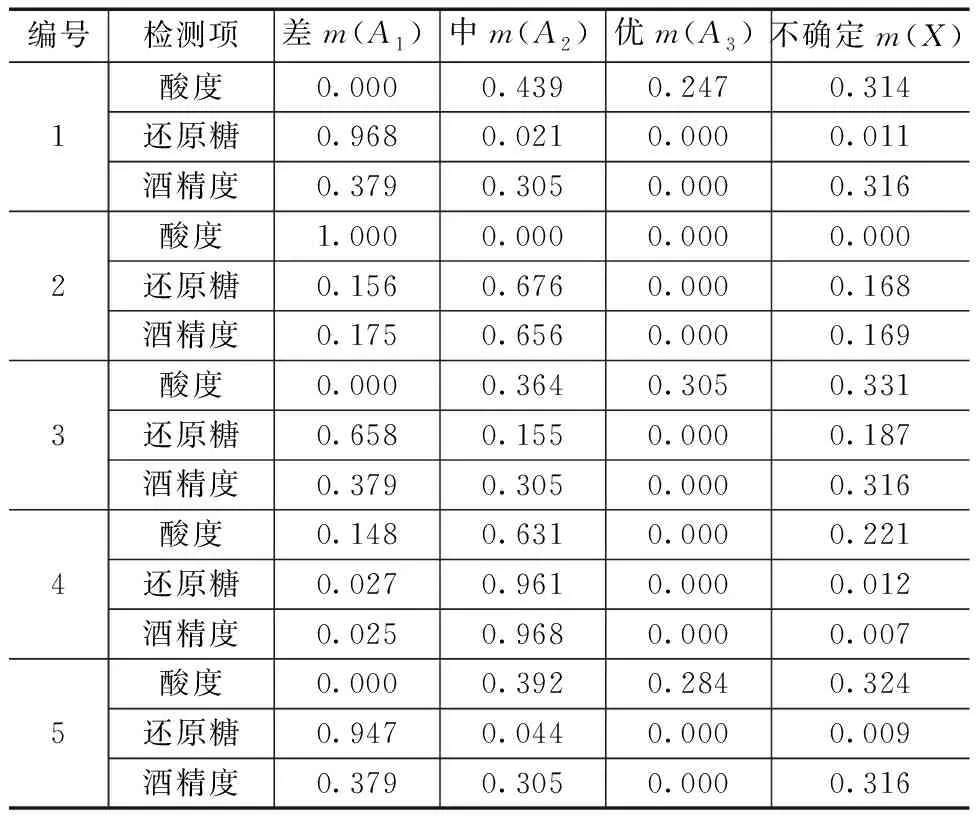
表3 黄水样本所对应的概率分布
分析表3中的5个样本结果可以发现,不同黄水参数对各自发酵质量隶属度的基本概率分散于多个区间。除了样本4的3个隶属度均较集中分布于“中”,其他几个样本组在“差”“中”“优”3个区间均有分布,且存在基本概率为0的焦元。因此需要采用信息融合技术,进一步将各参数所反映的发酵质量进行综合评估。
3 D-S证据理论的改进
3.1 D-S证据理论的基本原理
D-S证据理论起源于1967年Dempster[16]提出的多值映射导出的上概率和下概率,之后其学生Shafer进一步将其完善,建立了命题和集合之间的对应关系,把命题的不确定性问题转化为集合的不确定性问题,满足比概率论弱的情况,形成了一套关于证据推理的数学理论。
证据理论在多传感器数据融合、多源信息融合中得到了广泛的利用,已成为一种基本的、重要的融合算法。
D-S证据理论的基本原理和计算规则如下。
设U为识别框架,基本信任分配函数m是一个从集合2U到[0,1]的映射,A表示识别框架U的任一子集,记作A⊆U,且满足
(1)
式中:m(A)为事件A的基本信任分配函数,它表示证据对A的信任程度。
假设辨识框架U下两证据的基本信任分配函数分别为m1和m2,焦元分别为Ai和Bj,则D-S组合公式为
(2)
(3)
式中:K反映了各个证据之间的冲突程度,称为冲突系数,范围为[0,1]。K值越接近1,表明证据间冲突越大;越接近0,表明冲突越小。当K=1时,两证据完全冲突,无法合成;当K>1时,合成结果将没有意义。系数1/(1-K)称为正则化因子。
3.2 冲突系数的改进
3.2.1 组合规则不合理的论证
对于D-S证据理论,K是表示证据间冲突大小的物理量。面对证据中含有概率分配为0的焦元时、证据间存在较大冲突时、或在同一证据中存在内部焦元时,使用D-S证据理论进行信息融合,可能会产生完全不合理的组合结果[17]。例如,当K过大时,组合结果容易出现与事实不符的情况,具体可通过以下例子来说明。
(1)假设对于识别框架U={A1,A2,A3},存在两个证据m1和m2,各自焦元的概率分配为
(4)
从而可计算出冲突系数K为0.96,进一步可得到证据理论的组合结果为
m(A1)=0,m(A2)=1,m(A3)=0
(5)
这显然与事实不符,也验证了证据理论在规则的组合方面确实存在不合理的地方。产生这一现象的根本原因是焦元含有为0的基本概率分配,按照传统融合规则,这会直接导致该部分的组合结果也为0。
(2)对于框架U,当基本概率分配为
(6)
此时两个证据具有完全相同的焦元与基本概率分配函数,但依然存在冲突系数K=0.34,这也说明了合成规则的不合理。
(3)对于框架U,当基本概率分配为
(7)
相较于式(5),这一概率分配数值完全相同,但在中间的焦元存在包含关系,最终冲突系数K=0.18,与式(5)不相同。这说明在同一证据中,内部焦元分配发生变化时,也会引起冲突系数K的变化。
综合以上分析可知,证据理论在组合规则上存在的主要缺陷包括:当证据中含有概率分配为0的焦元时,可能会产生完全不合理的组合结果;证据间的冲突考虑不合理,以致完全相同的两组证据进行组合后会由于冲突系数的存在而与原证据产生偏差;未考虑内部焦元的分配对冲突系数的影响。
3.2.2 改进的冲突系数
对于识别框架U={A1,A2,…,An},存在两个证据m1和m2,它们的概率分配函数分别为
(8)
考虑到为0的概率分配函数可能对组合所产生的巨大影响,因此将各证据与其自身进行组合,与自身组合结果可写为
m(AR)=
(9)
式中:AR为两焦元的交集;m1(Ai)为证据m1的第i个焦元。
由于内部各焦元的基本概率分配是相互影响的,同一证据内部焦元间也存在冲突,因此当某证据与自身进行组合时需考虑焦元内部所产生的冲突因素。结合证据理论关于冲突系数的计算公式,定义同一证据自身冲突系数KY为
(10)
式中:Ai、Aj分别为证据m1与m2的两个焦元。
类似的,不同证据间的冲突系数KN为
(11)
由于每条证据理论各次的组合结果所得的焦元概率必须满足和为1的原则,因此可将各次组合写成交集为空与交集不为空两种情况之和,即
(12)
由于冲突系数K为所有交集为空集的和,因此当有两条证据进行组合时,它们的总冲突系数KTotal为
KTotal=K11+K22+K12+K21=
(13)
相比传统的冲突系数,KTotal可以较全面包含各证据间的冲突及证据与自身组合的冲突。
对两个证据进行组合时,共有22种组合方式,从而这4种组合方式的概率之和为4,另外由于焦元的概率综合等于总的概率和减去冲突概率之和,因此可得到两个证据组合时的组合规则为
m(AR)=
(14)
同理,当对n个证据进行组合时,组合规则为
m(AR)=
(15)
3.3 改进后的D-S证据理论
改进后的计算规则如下。

(16)
(2)计算各证据到参考证据的偏差di。
(17)
(3)设定证据可信度分级系数wi。信度级数为10级时,根据各证据的证据可信度可根据距离的值来确定分级系数的公式为
(18)
式中:Δd=dmax-dmin。
(4)根据信度分级系数可得到加权系数ci。
(19)
(20)
4 发酵质量评价
对于表3中黄水样本的基本概率分配,首先采用传统D-S证据理论进行信息融合,组合结果见表4。表4的结果中,存在多个概率分配为0的极端结果,融合结果没有完全体现表3所反映的发酵质量信息;同时不确定的概率分配较大,影响对于判断结果的解读;前后数据对比发现融合结果存在一定出入。例如,表3中样本5的还原糖和酒精度都反映发酵质量为差,而表4中的融合结果却是中。
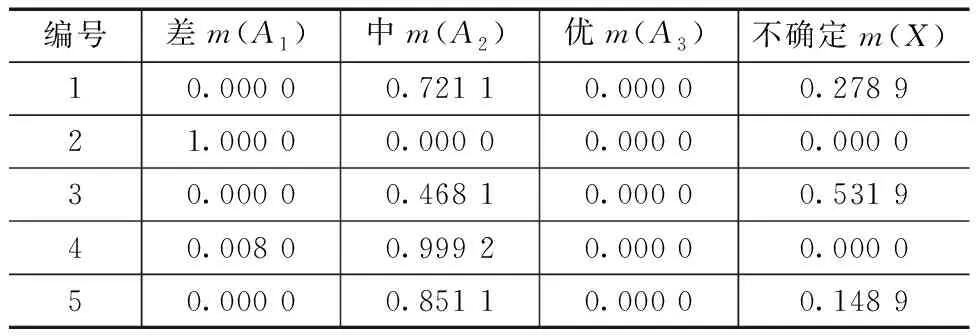
表4 传统D-S证据理论组合结果
然后采用改进的D-S证据理论的规则进行结合,最终所得结果汇总见表5。表5的结果中,不确定部分明显减少,同时各个概率区间的分配数据能够较为全面地反映发酵质量的评估结果,并且与表3中的原始数据一致。例如,样本1融合结果为差、样本2融合结果为中、样本5融合结果为差。
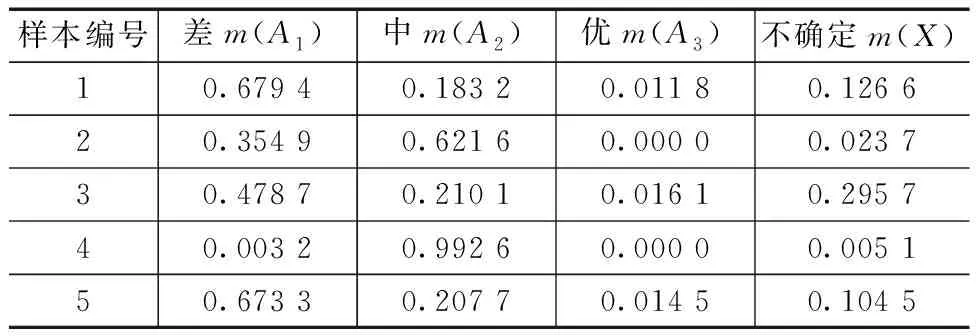
表5 改进后的D-S证据理论组合结果
对比表4和表5数据可以发现,改进后的D-S证据理论,有效降低了概率分配为0的焦元所产生的影响,使融合结果更加具有代表性;同时降低了不确定部分的分配概率。将评估结果分别与表2中的生产数据进行分析对比,发现改进后的D-S证据理论评估结果与实际更接近。
5 结论和展望
基于黄水检测数据,通过云模型,得到了定量黄水理化数据向定性发酵质量的映射结果;通过D-S证据理论,将不同黄水参数所反映的发酵质量进行融合评估;最终,通过将模糊理论和信息融合技术相结合,最终得到一种快速评估白酒发酵质量的方法。
在这个过程中,对D-S证据理论的冲突系数计算方式进行改进。改进后的D-S证据理论有效降低了冲突焦元的影响以及概率分配的不确定性,对发酵质量的评估结果更准确。最终得到一种可靠的浓香型白酒发酵质量的综合评估方法,有助于在浓香型白酒生产工艺中,降低人工判别的主观性。
对浓香型白酒发酵产物和副产物的快速检测技术以及信息融合分析技术,有利于推进在白酒生产过程中的自动化和数字化转型,推动白酒行业的发展。

