基于DEM的沥青混合料劈裂强度尺寸效应

肖宏宇, 赖志钦, 罗新华, 谢 斌, 赵高伟, 彭 成

(1.赣州康大高速公路有限责任公司, 江西 赣州 341000; 2.湘潭大学土木工程学院, 湖南 湘潭 411105)

尺寸效应是岩石、混凝土等脆性材料存在的普遍现象[1],即随着材料尺寸的增大,其强度会降低。沥青混合料与岩石材料类似,具有非均质性,沥青混合料内部微观裂缝的发展主要受其颗粒级配、尺寸等影响,而微观裂缝的发展演化最终会导致宏观结构的破坏。为准确描述尺寸变化对不同级配的沥青混合料劈裂抗拉强度的影响,系统性研究沥青混合料抗拉强度的尺寸效应现象显得极其重要。

近年来,国内外对于尺寸效应的研究大多数集中在用试验、理论或数值模拟的方法研究岩石[2-3]、混凝土[4-5]等脆性材料的尺寸效应上,并取得了一定的成果。伍法权等[6]进行了针对小尺寸岩样的单轴压缩尺寸效应研究,发现不同岩样中孔隙的大小、形状和分布情况对尺寸效应的变化趋势具有显著影响。金浏等[7]对不同骨料粒径下混凝土的动态拉伸破坏行为进行了研究,并提出了一种“静动态统一”尺寸效应理论公式来描述混凝土拉伸强度与试件尺寸之间的定量关系。唐伟等[8]应用数值模拟方式对不同围压下岩石试样的尺寸效应进行了研究分析,结果表明围压越大,岩石的尺寸效应越不明显。Zhang等[9]与王创业和杜晓娅[10]采用数值模拟方法研究分析了岩石单轴抗压强度与变形模量的尺寸效应的来源。李冬等[11]利用数值模拟方法,从两个角度验证了钢筋混凝土构件的尺寸效应的研究分析方法的合理性。徐快乐等[12]的研究表明,岩石的劈裂抗拉强度不仅与岩石的厚径比有关,还与试样的直径相关,并且对应抗拉强度呈现先陡后缓的降低趋势。张明等[13]的研究表明不同的加载方法对岩石试样的尺寸效应有明显的差异,且认为三点弯曲试验强度的尺寸效应最为显著。Ge等[14]研究分析了粗集料性能、最大公称粒径及加载速率3种不同方式对沥青混合料尺寸效应的影响。宿辉等[15]采用离散元数值模拟方法重构岩石样本并分析影响颗粒尺寸效应的因素,研究表明特征长度比越大,模拟结果越稳定。

目前,国内外关于脆性材料尺寸效应的研究成果层出不穷,但对于沥青混合料劈裂强度的尺寸效应的研究鲜见报道。因此,本文利用离散元方法(discrete element method,DEM)对不同级配、不同尺寸的沥青混合料进行巴西劈裂试验,进一步探究沥青混合料的劈裂抗拉强度尺寸效应特征,并基于此对沥青混合料抗拉强度的临界尺寸与临界强度进行计算,以期为室内试验中试样的制备及沥青混合料抗拉强度的稳定性评价提供一定的理论参考和技术支撑。

1 数值模型的构建及验证

1.1 离散元数值模型的构建

沥青混合料作为一种多相复杂体系材料,其内部存在多样的细观接触。在建立沥青混合料离散元数值模型过程中,需采用不同类别接触模型对其各类细观接触行为进行表征。通常而言,需考虑的细观接触类别包括集料-集料接触、集料-沥青砂浆接触、沥青砂浆-沥青砂浆接触和集料内部单元接触。在本研究中,采用独立的随机多面体颗粒进行集料颗粒的构建,因而集料内部之间的接触作用可以不予考虑。针对余下3类细观接触,选定线性接触模型、Burgers黏弹性接触模型以及平行黏结接触模型对其细观相互作用进行表征[16]。具体接触模型设定见表1。

表1 离散元数值试样接触模型

数值模型构建的过程中,采用离散元方法(DEM)生成圆柱体沥青混合料试样,试样尺寸依据《公路沥青路面设计规范》(JTG D40—2017)[17]进行设定(半径为50 mm,高度为63.5 mm的圆柱体),试样的级配分布为规范[17]中的级配中值。试样建模时不沿用以往研究中用球体代替粗集料的粗糙建模方式,而是先获得试样粗集料的不规则形状并将其轮廓导入虚拟模型中,然后在试样尺寸空间内随机生成具有级配特征的粗集料。用规则排列的颗粒填充粗集料之间的空隙部分,其中粒径在2.36 mm以下的颗粒视作沥青砂浆,粒径大于2.36 mm的颗粒为粗集料。最后在沥青砂浆单元部分随机删除一定数量的颗粒作为空隙,形成具有一定孔隙率的离散元数值模型试样,如图1所示。

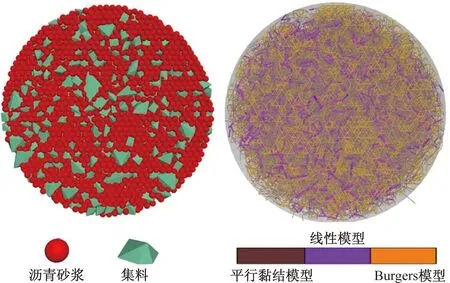
图1 离散元数值模型试样

具体采用的虚拟劈裂试验加载模型如图2所示。离散元模拟沥青混合料巴西劈裂试验的主要步骤是给予上方刚性墙体一个固定的速率,使刚性墙沿箭头所指方向向模型中间运动[图2(a)],然后根据刚性墙体受到虚拟模型的反作用力来确定模拟试验中相对应的轴向力并绘制试样的力-位移曲线[图2(b)]。

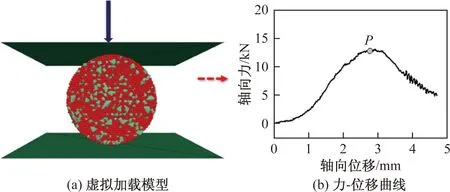
图2 虚拟试样加载模型及力-位移曲线

数值模型试样的劈裂抗拉强度的计算参考文献[18],其计算公式为

(1)

式中:σ为抗拉强度;P为峰值点加载力;R为试样半径;t为试样厚度。

1.2 数值模型细观参数设定

对于离散元数值试样而言,其宏观强度特征由其细观接触参数决定。考虑到其细观参数和宏观参数之间不存在十分明确的理论关系,因而目前多采用试错法[19]对离散元数值模型微观接触参数进行确定。在采用试错法进行模型参数标定过程中,需不断调整模型参数进行试算,当数值试验结果与室内试验结果吻合较好时,即认为该模型参数可有效反映试样的宏观力学特征[20]。本研究利用文献[21]中对于标准尺寸的级配AC-13沥青混合料试样的抗拉强度试验数据进行模型细观参数标定,通过采用不同的细观参数开展数值试验,最终获得理想的离散元数值模型细观参数,见表2。

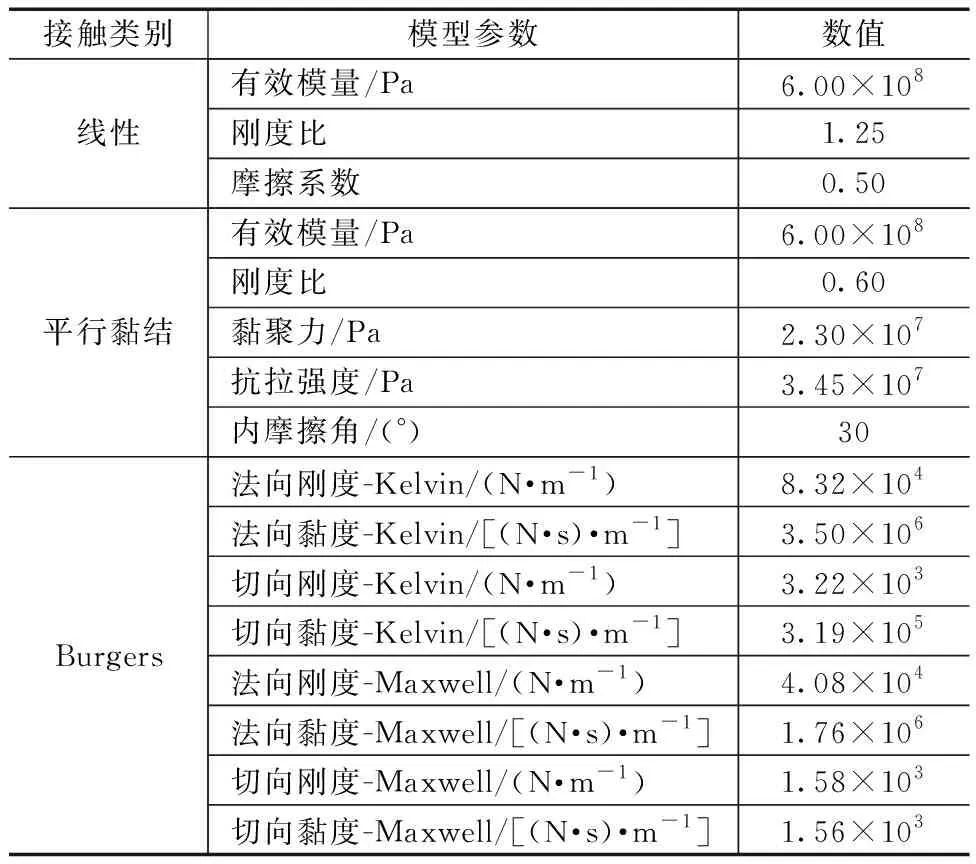
表2 离散元数值模型细观参数

结果表明,虚拟数值试验获得的力-位移曲线变化趋势与室内试验[21]结果较为接近(图3)。数值试验和室内试验所获得的轴向力峰值分别为12.90 kN和12.62 kN,两者的峰值强度虽然有些许差异,但考虑到本研究的目的在于寻找沥青混合料的抗拉强度与试样尺寸之间存在的规律,因此可认为该模型参数可有效地反映实际沥青混合料试样的宏观力学特性。

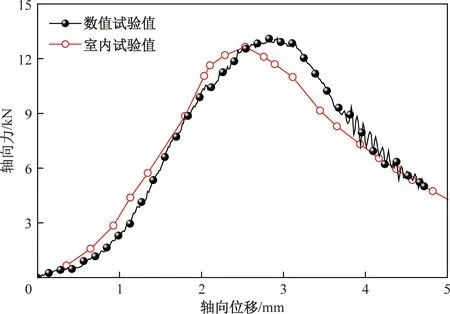
图3 数值模型验证结果

1.3 数值试验方案

为避免单一级配模拟结果的偶然性,以4种级配(AC-13、AC-16、AC-20、AC-25)下的沥青混合料试样为例,系统性评价不同级配(即不同的粗集料最大粒径尺寸)对试样尺寸效应的影响,其中各级配的粗集料最大粒径尺寸分别为16、19、26.5、31.5 mm,不同级配的沥青混合料数值试样如图4所示。除针对不同级配的沥青混合料开展数值试验外,另需对相同级配下不同尺寸的试样进行数值试验,以期获得不同级配的沥青混合料抗拉强度的尺寸效应特征。为更便捷地量化不同尺寸数值试样的尺寸特征,设定尺寸缩放系数对各试样之间的尺寸关联性进行表征,尺寸缩放系数α为

(2)

图4 4种级配沥青混合料数值试样

式中:Rs和ts分别为标准试样的半径及厚度值,分别为50 mm和63.5 mm;R和t分别为不同尺寸数值试样的半径及厚度值。

在数值试验过程中,为充分探究不同级配沥青混合料试样的尺寸效应特征,针对不同级配的沥青混合料试样,分别将尺寸缩放系数设定0.6、0.8、1.0、1.2、1.4以制备得到不同尺寸的数值试样,并进一步针对所设定试样开展劈裂抗拉强度数值试验以测定其抗拉强度值。

2 数值试验结果分析

2.1 力-位移曲线特征

深入分析巴西劈裂试验中试样在各个阶段的微观裂缝发展情况。以尺寸缩放系数为1.0且级配为AC-13的试样为例,详细分析各个阶段(A、B、C、D)试样的微观力学特征(图5)。在阶段A,试样的轴向力和位移较小,微观裂缝仅在加载墙体附近出现。随着试样进入阶段B,力和位移增大,微观裂缝开始向试样中间扩展。当试样进入阶段C时,力和位移达到峰值,内部微观裂缝基本贯通试样并向试样表面扩展。而在试样进入阶段D时,力和位移逐渐减小,微观裂缝完全贯通试样并在试样表面形成肉眼可见的宏观裂缝。

图5 标准尺寸试样的加载曲线

对不同级配类型且尺寸各不相同的虚拟试样开展巴西劈裂试验,获得不同级配下沥青混凝土的轴向力-轴向位移曲线,且每条曲线的变化规律基本相同。以4种级配(AC-13、AC-16、AC-20、AC-25)为例,系统性分析沥青混凝土在巴西劈裂过程中的力-位移曲线的变化规律。不同级配试样的力-位移曲线如图6所示。

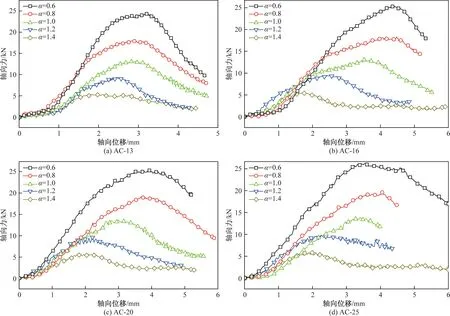
图6 4种级配沥青混合料力-位移曲线

级配相同时,以级配AC-13的试样为例进行分析计算。尺寸缩放系数为0.6的试样峰值力为24.44 kN,峰值处轴向位移为3.19 mm;而尺寸缩放系数为0.8的试样峰值力为17.98 kN,峰值位移为2.84 mm,相比前者,峰值力减小幅度为26.43%,峰值位移减小幅度为10.97%;当试样尺寸缩放系数从0.8增大至1.0时,峰值力减小幅度为27.92%,峰值位移减小幅度为11.41%;进一步增大尺寸缩放系数,从1.0到1.2时,峰值力与位移减小幅度分别为27.78%和12.50%;从1.2到1.4时,峰值力与位移减小幅度分别为42.74%和26.94%。由图6可知,其余各级配试样的峰值力与峰值位移也随着尺寸缩放系数的增大而减小,且减小幅度在逐渐增大。结果表明,级配一致时,试样尺寸越大,峰值力和峰值位移越小,且随着试样尺寸的增大,试样峰值力和峰值位移的差距在逐渐增大。

级配不同时,以级配AC-16的试样为例进行分析计算。尺寸缩放系数为0.6的试样峰值力为25.21 kN,峰值位移为4.36 mm;当尺寸缩放系数增大至1.4时,试样峰值处的力与位移分别为5.48 kN和1.78 mm,峰值点力与位移的下降幅度分别为78.26%和59.17%。在其余级配(AC-13、AC-20、AC-25)下的试样中,峰值点的力与位移的下降幅度分别为78.07%与43.89%,77.78%与49.44%以及77.97%与47.19%。结果表明4种级配下沥青混合料的力-位移曲线随尺寸缩放系数的增大呈现出相同的变化规律,说明沥青混合料是否具备尺寸效应现象不会因级配组成的变化而改变。

2.2 抗拉强度的尺寸效应

为研究不同级配的沥青混合料抗拉强度的尺寸效应,根据数值试验以及式(1)得到不同级配下各尺寸试样的劈裂抗拉强度(图7)。同时,为更直观地表征抗拉强度与尺寸缩放系数的关系,根据文献[22]的研究成果,采用式(3)对抗拉强度的尺寸效应进行拟合,拟合曲线如图7所示。

(3)

图7 4种级配沥青混合料尺寸效应拟合曲线

式中:k和b为尺寸效应相关系数。

由图7可得:①随着试样尺寸缩放系数的增大,沥青混合料的劈裂抗拉强度可以用式(3)较好地拟合,在尺寸缩放系数达到1.2以上时,沥青混合料的抗拉强度逐渐趋于稳定。②不同级配下的试样尺寸大小对抗拉强度有明显的影响。以级配AC-25的试样为例进行分析计算时,当尺寸缩放系数为0.6时,试样的劈裂抗拉强度为1.60 MPa。随着尺寸缩放系数增大至1.4,试样的劈裂抗拉强度降至1.32 MPa,下降幅度为17.50%。在其余3种级配(AC-13、AC-16、AC-20)下,试样的抗拉强度下降幅度分别为18.67%、18.54%、18.18%。结果表明,4种级配试样的抗拉强度均存在尺寸效应,且抗拉强度的下降幅度随着粗集料尺寸的增大而减小。

依据苏捷和方志[22]的研究成果,尺寸效应相关系数k×b的值越大,尺寸效应越明显,k×b的值与4种级配之间的关系曲线如图8所示。由图8可知,尺寸效应相关系数有减小趋势,且试样级配从AC-13增大至AC-25时(即试样粗集料最大粒径尺寸从16 mm增大至31.5 mm),尺寸相关系数的乘积从0.323 4逐渐减小到0.305 2且级配AC-25的试样尺寸相关系数分别约为其余级配试样的94.37%、96.47%、97.96%。结果表明,随着试样级配的增加(即试样粗集料尺寸的增大),试样的抗拉强度尺寸效应在减弱,且4种级配中级配AC-13的抗拉强度尺寸效应最为明显。

图8 4种级配下的尺寸相关性

2.3 临界尺寸及临界抗拉强度特征

由式(3)可知,随着沥青混合料试样的尺寸逐步增大,其抗拉强度逐步减小,呈现出典型的尺寸效应。此外,对于不同级配类型沥青混合料而言,其抗拉强度的尺寸相关性亦存在一定区别。由式(3)计算得到不同级配类型沥青混合料临界尺寸缩放系数αcr以及临界抗拉强度σcr,见表3。

表3 4种级配沥青混合料临界尺寸及临界强度

为更直观地获得不同级配类型沥青混合料临界尺寸和临界抗拉强度关系特征,将表3中的结果进一步处理得到图9中的关系曲线。由图9可知,随着试样级配的增加(即试样粗集料尺寸的增大),沥青混合料抗拉强度的临界尺寸有减小趋势,临界强度值不断增大。级配AC-13试样的临界尺寸值分别是级配AC-16和级配AC-20试样的101.13%和102.29%,主要原因是级配AC-13试样的尺寸效应更为明显;试样级配从AC-20增大到AC-25时(即试样粗集料最大尺寸从26.5 mm增大至31.5 mm),沥青混合料的临界尺寸缩放系数均为1.750,但临界抗拉强度从1.216 MPa增大至1.261 MPa。结果表明粗集料最大尺寸大于26.5 mm时,粗集料尺寸增大对临界尺寸的影响可忽略不计,但对临界抗拉强度依旧有明显的影响。

图9 4种不同级配下的尺寸临界特征

3 结论

(1)不同级配的沥青混合料抗拉强度均有着较明显的尺寸效应,主要表现为试样尺寸越大,抗拉强度越低。尺寸缩放系数为1.4的各级配(AC-13、AC-16、AC-20、AC-25)试样的抗拉强度分别比0.6的各级配试样的抗拉强度下降了18.67%、18.54%、18.18%、17.50%。

(2)沥青混合料抗拉强度的尺寸效应现象与粗集料尺寸有着密切关系,级配越大,粗集料尺寸越大,抗拉强度的尺寸效应越不明显。级配AC-25的试样抗拉强度的尺寸相关系数分别约为级配AC-13、AC-16与AC-20试样的94.37%、96.47%、97.96%,表明4种级配中AC-13的抗拉强度尺寸效应更为明显。

(3)随着粗集料最大粒径尺寸的增大,沥青混合料抗拉强度的临界尺寸有减小趋势,并趋于平缓,临界强度值不断增大。级配AC-13试样的临界尺寸分别是级配AC-16、AC-20、AC-25试样的101.13%、102.29%、102.29%。

(4)级配AC-20和AC-25试样抗拉强度的临界尺寸均为1.750,则粗集料最大粒径尺寸大于26.5 mm时,粗集料尺寸对试样抗拉强度的临界尺寸基本无影响。