GFRP筋土钉支护钉头的锚固性能

刘军 宋晔 张建全 牛大伟

DOI： 10.11835/j.issn.2096-6717.2022.033

基金项目：北京市自然基金-北京市教委联合资助重点项目（KZ201810016021）；北京未来城市设计高精尖创新中心资助项目（UDC2019032824）

作者简介：刘军（1965- ），男，博士，教授，主要从事岩土工程与地下工程研究，E-mail：liujun01@tsinghua.org.cn。

Received： 2022?01?08

Foundation items： Beijing Municipal Natural Science Foundation-Key Project of Beijing Municipal Education Commission （No. KZ201810016021）; Beijing Advanced Innovation Center for Future Urban Design， Beijing University of Civil Engineering and Architecture （No. UDC2019032824）

Author brief： LIU Jun （1965- ）， PhD， professor， main research interests： geotechnical and subsurface engineering， E-mail： liujun01@tsinghua.org.cn.

（1. 北京建筑大学 土木与交通工程学院，北京 100044； 2. 北京城建勘测设计研究院有限责任公司，北京 100101； 3. 北京巖土工程协会，北京 100005）

摘要：土钉钉头为土钉墙整体结构中的薄弱部位，为研究土钉钉头锚固性能，以一种装配式柔性面层GFRP筋土钉墙为例，通过室内钉头锚固性能试验及三维数值模拟对外径32 mm的中空GFRP筋钉头的极限抗拉强度、钉头变形及破坏规律进行研究。研究结果表明，该GFRP筋钉头极限承载力在240～290 kN之间，当螺母拧紧时螺纹副的应力主要分布在螺纹牙前3环，其中以钉头第1环螺纹牙应力集中现象尤为明显；此外，采用螺纹展开法建立钉头螺纹牙的力学模型，得出了第1环螺纹极限剪切强度与钉头极限荷载之间的关系，并通过计算得出该GFRP筋钉头极限承载力为244.54 kN，与试验结果相符。通过室内钉头锚固性能试验的脆性破坏特点，确定GFRP筋钉头安全系数在1.8～2.0之间，并判定此种GFRP筋安全荷载在125～135 kN之间。

关键词：基坑；GFRP筋土钉；土钉墙；钉头；锚固性能

中图分类号：TU433     文献标志码：A     文章编号：2096-6717（2024）03-0094-09

Anchorage performance of nail head for GFRP bar soil nail support

LIU Jun¹， SONG Ye¹， ZHANG Jianquan²， NIU Dawei³

（1. School of Civil and Transportation Engineering， Beijing University of Civil Engineering and Architecture， Beijing 100044， P. R. China； 2. Beijing Urban Construction Exploration & Surveying Design Research Institute Co.， Ltd.， Beijing 100176， P. R. China； 3.Beijing Geotechnical Engineering Association， Beijing 100005， P. R. China）

Abstract： The soil nail head is the weak point in the overall structure of the soil nail wall. In order to study the anchorage performance of soil nail head， this paper takes an assembled flexible surface GFRP reinforced soil nail wall as an example. Through indoor nail head anchorage performance test and 3D numerical simulation the ultimate tensile strength， nail head deformation and damage pattern of hollow GFRP bar nail head with 32 mm outer diameter were investigated. It was found that the ultimate load bearing capacity of such GFRP bar nail head is between 240 kN and 290 kN. When the nut is tightened， the stress of the thread is mainly distributed in the first three rings of threaded teeth， with significant stress concentration exists at the first ring of threaded teeth in the head of the nail. In addition， a mechanical model of the threaded tooth of the nail head was developed using the thread expansion method， and the relationship between the ultimate shear strength of the first ring thread and the ultimate load on the nail head was derived. The ultimate load-carrying capacity of this GFRP bar nail head was calculated to be 244.54 kN， which is consistent with the test results.The brittle damage characteristics of the indoor nail head anchorage performance test determined that the safety factor of GFRP tendon nail head is between 1.8 and 2.0. It is also determined that the safe load of such GFRP tendons is between 125 kN and 135 kN， providing a reference for the research and application of similar projects.

Keywords： foundation pit； GFRP bar soil nail； soil nail wall； nail head； anchorage performance

土钉墙作为基坑工程中的一种重要支护形式應用领域极为广泛，如城市轨道交通、地下综合管廊、地下市政管线、工业与民用建筑等^[1]。但传统土钉墙不仅消耗能源、浪费资源，还污染地质环境^[2]。为解决这一问题，采用GFRP筋作为新型土钉代替传统钢筋土钉已成为一个新的趋势。GFRP筋为一种新型建筑材料，低碳、环保、节约能源，比传统钢筋耐腐蚀，抗拉强度也高于钢筋^[3]，且具有良好的大气稳定性^[4]，其作为钢筋土钉的替代品已在基坑支护工程中获得一定程度的应用^[5-10]。

根据《建筑基坑支护技术规程》（JGJ 120—2012）^[11]，土钉支护安全稳定性设计主要包含土钉轴向拉力计算及土钉极限抗拔承载力计算两方面。其中，土钉轴向拉力与土体压力呈正相关，土钉极限抗拔承载力为土钉轴向拉力的1.4～1.6倍。因此，对于传统钢筋土钉而言，土钉设计的薄弱位置主要为注浆粘结段，其主要破坏形式为注浆粘结段滑脱。然而，GFRP筋为玻璃纤维及树脂挤压而成的各向异性材料^[12-13]，其抗拉强度远大于抗剪强度，但GFRP土钉在受拉力作用下，其钉头受力主要表现为螺纹牙受剪，因此，在GFRP土钉支护安全稳定性设计时，不能仅考虑土钉轴向拉力及土钉极限抗拔承载力，还应对将土钉钉头的极限受剪承载力加以考虑。对于这一薄弱位置，张杰等^[14]采用塑料螺母和金属螺母两种不同锚固方式对GFRP筋进行拉拔试验，发现塑料螺母在拉拔过程中出现螺母破坏，金属螺母在拉拔过程中出现筋材螺纹摩擦破坏；高洋^[15]发现螺母承载力是GFRP筋材所有力学性能中的弱项，螺母发生破坏或滑脱时远小于杆体极限拉应力；何杰等^[16]通过矿井现场监测发现，GFRP筋最大受力是筋材极限抗拉强度的85.7%，而螺纹锚固位置极限承载力为筋材极限抗拉强度的57%，为整体结构中最薄弱部位。因此，GFRP土钉钉头锚固在整个土钉墙支护体系中极为重要，而在实际工程中也存在土钉钉头发生破坏而导致的基坑支护结构失稳、边坡滑移等工程事故，但目前系统针对土钉钉头方面的研究极少。

针对这一问题，笔者以一种装配式柔性面层GFRP筋土钉支护构造中的钉头为例，通过室内钉头锚固性能试验及数值模拟的方法分析研究了钉头的变形破坏规律。研究发现，GFRP筋钉头在螺栓拧紧时螺纹副上的应力主要分布在螺纹牙前3环，其中以钉头第1环螺纹牙应力集中现象尤为明显；并采用螺纹展开法建立了钉头第1环螺纹牙的力学模型，得出了第1环螺纹极限剪切强度与钉头极限荷载的关系。并结合室内试验、三维数值模拟及力学模型，计算得到此种公称外径为32 mm的中空GFRP筋钉头的极限荷载在250 kN左右，并确定其安全系数为1.8～2.0，实际应用安全荷载为125～135 kN。此外，证明此种土钉支护钉头可以承担实际工程中土钉钉头所需承担的应力。

1 GFRP筋钉头锚固性能试验

在实际工程中，钉头为此种GFRP筋土钉支护体系中的薄弱部位，需对其锚固性能进行研究。

1.1 装配式柔性面层GFRP筋土钉支护构造组成

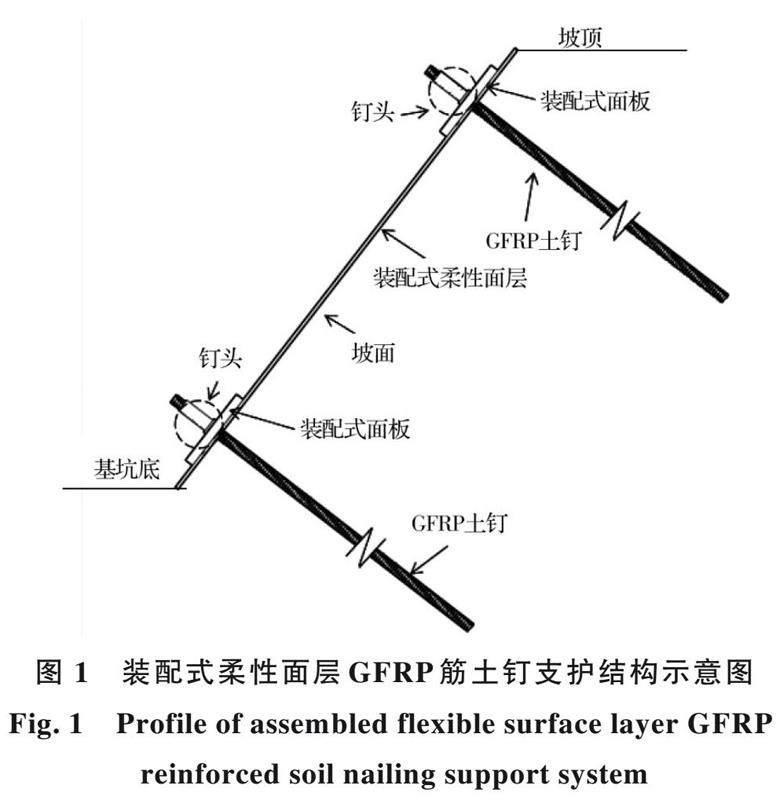
装配式柔性面层GFRP筋土钉支护结构如图1所示，装配式构件包括装配式面板和柔性面层，装配式面板材质为玻璃纤维增强聚合物，其长×宽×高为30 cm×30 cm×3 cm，中间留有直径为50 mm的土钉孔；柔性面层为土工布；两者可重复利用。土钉采用大直径的中空GFRP筋，公称外径32 mm，内径15 mm，可从中空处灌浆。如图2所示，钉头由GFRP筋、螺母、垫板组成，由螺母将GFRP筋通过垫板固定在GFRP筋面板上。GFRP筋密度为1.98 g/cm³，树脂含量为体积含量的28%；螺母材质为20铬锰钛，其外径为44 mm，内径为32 mm，内部螺纹与GFRP土钉上的螺纹适配；垫板材质为钢，其长×宽×高为6 cm×6 cm×1 cm，中间留有直径为34 mm的土钉孔。

1.2 试验设计及加载

为验证该GFRP筋材在实际工程中应用的可行性，对GFRP筋材随机取样6根进行检测。所有抽检GFRP筋材外观质地均匀、无气泡裂纹，螺纹牙距整齐。杆体直径、直线度、抗拉强度、剪切强度的检测结果如表1所示。由表1可见，所有抽检GFRP筋均符合技术要求。

为研究钉头的锚固性能，依据《预应力筋用锚具、夹具和连接器》（GB/T 14370—2015）^[17]采用穿心式张拉机进行试件组装后（图3）对GFRP筋进行钉头锚固性能试验，试验参数及数量见表2。

将GFRP筋安装在如图4所示的张拉机上，筋材一端为工具锚，采用40 cm的钢套筒并通过环氧树脂加固，以防止发生位移；另一端为钉头。

在进行GFRP筋钉头锚固性能试验时，按照《预应力筋用锚具、夹具和连接器》（GB/T 14370—2015）^[17]中的内容，对筋材进行分级加载，初应力可取GFRP筋极限荷载的10%，加荷速度不超过1.5 MPa/s；此后每级分别以GFRP筋极限荷载的20%、40%、50%进行匀速加载，加载速度不超过3 MPa/s；由GFRP筋极限荷载的10%开始，每当增加一级荷载后，需持荷5 min；直至加载到最高一级荷载，持荷10 min，然后继续缓慢进行加载至试件破坏。

1.3 试验结果及变形破坏过程

钉头锚固性能试验中，6个试件的荷载-位移曲线如图5所示。

由图5可以看出，试验开始时，先施加GFRP筋极限荷载的10%作为初应力荷载，在初应力荷载作用下，钉头先出现较小的滑移预紧，滑移过后钉头与筋材共同受力，此时钉头位移随荷载的增加而增大，此外還可以观察到，荷载-位移曲线在整体上呈升趋势的过程中出现小幅度波动，这种波动是由于玻璃纤维增强聚合物中的纤维在受拉力作用下断裂产生的。但当筋材上承受的拉力继续增大，钉头螺母滑动，GFRP筋上的多环螺纹瞬间发生剪切破坏，钉头位移急速增加，整体曲线表现为明显的脆性破坏，螺母滑移后的钉头失去锚固性能，穿心式张拉机随即卸荷。钉头破坏情况如图6所示。

试验结果如表3所示，钉头极限荷载的平均值为259.6 kN，平均位移为2.1 mm，6个试件的钉头的极限荷载在240～290 kN之间，破坏前的钉头平均位移均在1.5～2.6 mm之间。

此外，6个试件在拉伸过程中GFRP筋均未出现筋材断裂或劈裂的情况，均未达到GFRP筋的极限荷载。

2 钉头变形破坏规律三维数值模拟

为进一步分析筋材受拉时，钉头变形破坏规律，以揭示破坏机理，采用ABAQUS有限元分析软件模拟GFRP筋钉头应力应变分布规律^[18]。

2.1 模型假设

钉头在受力的情况下，螺母与GFRP筋材之间呈拧紧状态，此时二者之间主要相互作用表现为螺纹牙受剪，采用ABAQUS软件进行数值模拟时，采用以下假定^[19]：1）不考虑螺母与GFRP筋材拧紧后螺纹间存在缝隙，假定螺母与GFRP筋材为之间已经拟合；2）不考虑螺栓预紧力；3）构件均为弹性变形，其应力应变关系取理想弹塑性。

2.2 模型构建及参数取值

2.2.1 模型构建赋予材料属性

依据构件实际尺寸，分别建立GFRP筋、螺母及垫板3个构件，如图2所示，将3个构件进行装配。创建名为玻璃纤维增强聚合物、20铬锰钛、钢的3种不同材料，计算参数表4所示，对GFRP筋材料属性设定为玻璃纤维增强聚合物，螺母材料属性设定为20铬锰钛，垫板材料属性设定为钢。

2.2.2 计算参数单元选取及网格划分

如图7所示进行网格划分。其中GFRP筋及垫板采用C3D8单元，螺母采用C3D10单元。

2.2.3 定义接触与约束

螺母与GFRP筋之间切线方向的摩擦系数设定为0.15，法线方向默认为“硬”接触。螺母与垫板之间采用tie连接，垫板与GFRP筋之间不设接触。

2.2.4 定义载荷及边界条件

拟定垫板的边界条件为完全固定，其X、Y、Z方向的位移及转角均为0。对GFRP筋施加拉力，施加的拉力大小分别为GFRP筋极限荷载的10%、20%、40%、50%、80%、100%共计6种，观察6种不同荷载下GFRP筋钉头产生的位移及钉头的应力分布情况，以此分析GFRP筋在拉力作用下钉头的应力应变规律。

模型采用Static，General分析步进行分析。

2.3 模拟结果分析

2.3.1 变形规律

当垫板固定时，对GFRP筋施加拉力，此时在拉力作用下，螺母与GFRP筋之间的螺纹产生摩擦接触，继而产生位移，产生的位移主要分为两方面，一是筋材受拉力作用后自身延长，二是钉头与GFRP筋之间轻微滑移，其变形模拟结果如图8所示。

整合数值模拟得到的结果，以筋材极限荷载的百分比为横轴，绘制不同拉力作用下钉头的位移曲线，绘制完成后的钉头位移-筋材极限荷载百分比曲线如图9示。

通过钉头位移-筋材极限荷载百分比曲线可以看出，GFRP筋在受拉力作用的情况下钉头位移随拉力增大而逐渐增大，当筋材所受拉力较小时，钉头位移的增长速率较为平缓，随着筋材所受拉力增大，钉头位移的增长速率逐渐增大，当拉力达到GFRP筋极限荷载的100%即350 kN时，钉头最大位移出现在钉头第1环螺纹牙上，最大位移为3.24 mm，由于拟定各构件均为理想弹性体，而实际情况中GFRP筋为玻璃纤维及树脂挤压而成的各向异性材料^[12-13]，其抗拉强度远大于抗剪强度，而钉头受拉力作用，主要表现为螺纹牙受剪，由此提取螺纹牙受剪方向的最大应力为283 kN，已超过GFRP筋的抗剪强度，且超过钉头锚固性能试验的结果259.6 kN。因此，在模拟中钉头承受应力为350 kN时，可判定钉头已经发生破坏，实际破坏时钉头位移应小于3.24 mm。

此外在拉力作用下，钉头的第1环螺纹牙上出现较为明显的应力集中，螺纹牙变形较大，如图10所示。在集中应力的作用下，此时螺纹牙的变形大致是由螺纹牙弯曲变形、螺纹牙剪切变形、螺纹牙根部倾斜变形及螺纹间接触变形4种复合而成，如图11所示，图中1号实线代表螺纹牙咬合线，2号实线代表未变形的螺纹牙，3号虚线代表变形后的螺纹牙。

2.3.2 破坏规律

当GFRP筋受拉力作用时，钉头处承受最大的应力，但此时钉头处的每环螺纹上所分布的应力并不均匀，在钉头的第1环螺纹上出现了极为明显的应力集中，导致第1环螺纹出现较大的变形，此处为整体模型受力强度最大且最薄弱的位置。当GFRP筋上所受拉力越来越大，钉头第1环螺纹上的应力集中情况更加明显，螺纹的变形也随之增大。

如果此时螺纹第1扣承受的应力超过了螺纹的极限剪切强度，则此处螺纹会出现剪切破坏，随后应力立即重新分布，导致下一环螺纹在重分布的应力作用下出现剪切破坏，以此类推，当数环螺纹均受剪破坏后，便会出现钉头滑脱的情况，即钉头的锚固作用失效。应当注意，若1环螺纹破坏后，其应力重分布速度极快，一旦1环螺纹剪切破坏发生便无法及时制止，将迅速导致钉头锚固作用失效。

综合GFRP筋钉头锚固性能试验与三维数值模拟中得到的结果，在数值模拟中，当拉力达到GFRP筋极限荷载的80%～100%，钉头处的螺纹牙会出现较大的变形，而在钉头锚固性能试验中，这种较大变形会导致筋材上的螺纹牙剪切破坏，钉头螺母滑脱并失去锚固性能。如果这种情况在工程中出现，则会导致这根失去钉头锚固作用的土钉无法继续承担土体压力，进而导致该根土钉失去支护作用，严重情况下会导致基坑坍塌。

3 钉头破坏的力学模型建立

在钉头锚固性能试验中，当钉头螺母发生滑移时，可以观察到GFRP筋上的螺纹有较为明显的破坏，而螺母上的螺纹并未破坏，且螺母的弹性模量远高于GFRP筋的弹性模量，故判定GFRP筋上的螺纹先于螺母上的螺纹发生剪切破坏，因此，将GFRP筋上的螺纹破坏作为薄弱点进行计算。

对单个受拉螺栓上的螺纹强度研究主要以其受到的预紧力为研究对象，并未考虑到各圈螺纹牙的变形，因此，不能简单地根据单个螺栓强度的计算方法来计算钉头的极限荷载。

颜庭梁等^[20]对单圈螺纹上的荷载与整体螺栓上的荷载进行了研究，即螺栓的伸长量及螺母的压缩量与螺纹累积变形量相等。因此，在其研究的基础上，根据数值模拟及室内试验，GFRP筋上第1环螺纹牙剪切破坏时钉头螺母滑脱失去锚固性能这一结果为依据，判定超过单圈螺纹牙极限荷载时钉头锚固作用失效，由此提出GFRP筋钉头极限荷载的计算方法。通过对GFRP筋材的伸长量及螺母的压缩量的计算，与GFRP螺纹的累计变形量进行对比分析，并将对比结果进行整理，建立了如式（1）所示的GFRP筋钉头极限荷载与单圈螺纹牙极限荷载的关系式。将式（1）应用在钉头破坏力学模型中。通过计算单圈螺纹的极限荷载及螺纹牙的变形，即可得出GFRP筋钉头安全荷载。 （1）

式中：为GFRP筋钉头安全荷载；为单圈螺纹牙极限荷载；为筋材上附加荷载影响系数，由GFRP筋上螺纹变形计算得到；为螺母上附加荷载影响系数，由螺母上螺纹变形计算得到；为GFRP筋上的螺纹横截面积；为GFRP弹性模量；为螺母上的螺纹横截面积；为螺母弹性模量；为螺纹中径；为螺纹啮齿线与水平线的夹角；为安全系数。

3.1 单圈螺纹荷载计算

根据Sopwith^[21]和Yamamoto^[22]的研究，计算螺纹强度时可以假定将筋材沿中心轴展开，将螺纹看作悬臂梁，展开效果如图12所示。此悬臂梁宽度为螺纹大径的周长即。单圈螺纹极限荷载为，其計算式如式（2）所示。作用在以螺纹中径为直径的圆周上，截面a-a为螺纹牙的危险截面。

截面a-a剪切强度计算式为（2）

式中：为单圈螺纹牙极限荷载；为GFRP筋材料的剪切强度；为螺纹中径；为螺距。

3.2 螺栓伸长及螺母压缩计算

螺栓伸长量及螺母压缩量是求取式（1）的重要内容，参考颜庭梁等^[20]的研究理念，将螺栓及螺母按照其螺纹啮合线进行展开，展开形式如图13所示。螺纹啮合线长度为，其与水平面之间存在为的螺旋升角，的计算公式如式（4）所示。拟定左端为O点，在单圈螺纹上均匀分布的沿螺栓径向的力为，可建立螺栓伸长量和螺母压缩量的计算式，如式（3）所示。 （3） （4）

式中：为螺栓伸长量；为螺母压缩量；为GFRP筋钉头荷载；为GFRP筋上的螺纹横截面积；为GFRP弹性模量；为螺母上的螺纹横截面积；为螺母弹性模量；为单圈螺纹长度；为螺旋升角；为螺距。

3.3 螺纹变形计算

在运用式（1）时需要对螺母上的螺纹变形及GFRP筋上的螺纹变形进行计算。此前在三维数值模拟中发现螺纹牙的变形有螺纹牙弯曲变形、螺纹牙剪切变形、螺纹牙根部倾斜变形及螺纹间接触变形4种，如图14所示。因此，将钉头的螺纹变形看作斜齿轮双齿啮合时齿牙的变形，采用齿轮齿牙弹性变形的计算方法^[23-24]，建立如图15所示的坐标系，4种螺纹牙变形计算公式如式（5）～式（8）所示。

螺纹牙弯曲变形 （5）

螺纹牙剪切变形    （6）

螺纹牙根部倾斜变形 （7）

螺纹间接触变形 （8）

式中：为C到原点的距离，C点为螺纹中径与y轴的交点；为；为齿轮转动的速率，此处取0；为弹性模量；为单圈螺纹牙极限荷载；为螺纹侧边与垂直于螺纹轴线的平面之间的夹角；为螺旋升角，即螺旋线切线与垂直于螺纹轴线的平面之间的夹角；为单圈螺纹长度。

内外螺纹累计变形为 （9）

式中：K_s、由式（9）计算得到。

查询螺栓尺寸表可知，直径为32 mm的螺栓的中径约为30.727 mm、小径约为29.211、螺距为3.5 mm，将螺纹尺寸带入式（9），可计算得出。

3.4 钉头极限荷载计算

在轴向拉力作用下，螺纹变形与螺栓伸长及螺母压缩量相同。将式（4）和式（9）带入式（10），同时对进行积分，即可推导得出式（1），发现其极限荷载与其抗剪强度呈正相关，与其螺纹参数呈负相关。并可算出此种GFRP筋钉头的极限荷载为244.54 kN。筋材上螺纹累计变形为1.44 mm，螺母上螺纹累计变形为0.86 mm，螺纹累计变形为2.30 mm。而室内试验中钉头的极限荷载在240～290 kN之间。力学模型计算结果与室内试验结果较吻合，由此得到钉头的极限荷载与GFRP筋的极限荷载之间的关系，得到钉头的极限荷载在GFRP筋极限荷载的60%～70%之间。但在实际工程中，为了防止钉头螺母滑移，钉头失去锚固性能的情况出现，需要对GFRP筋钉头的极限荷载进行安全系数折减，得出工程中允许使用的GFRP筋钉头安全荷载。 （10）

普通螺栓的安全系数取值在1.2～1.6之间，且先出现弹性变形，破坏前有预兆。而GFRP筋钉头依据其锚固性能试验得到的结果，在分级加载至破坏的过程中表现出明显的脆性破坏，在其破坏前不会出现预兆，故可将安全系数提高，因此，将GFRP钉头处提高安全系数后取值在1.8～2.0之间。

综合数值模拟、室内试验及计算所得的极限荷载，判定其极限荷载为250 kN，故此种GFRP筋钉头安全荷载在125～135 kN之间。此外综合实际工程中土钉受力的经验，土钉需要承担的极限拉应力一般在70～90 kN之间，故此种GFRP筋钉头满足实际工程中的需要。

4 结论

通过结合室内钉头锚固性能试验、三维数值模拟及钉头破坏的力学模型计算，对GFRP筋的钉头锚固性能进行了深入研究，得到如下结论：

1）得到了钉头在发挥锚固作用时的应力分布规律，即钉头在发挥锚固作用时，其应力并不均匀分布在每一环螺纹牙上，在钉头的第1环螺纹牙上出现较强的应力集中，第2环及之后的螺纹牙上应力明显变小。

2）建立螺纹牙受力计算模型，通过第1环螺纹能承受的极限剪切强度，提出了钉头极限荷载的计算方法，发现GFRP土钉钉头极限承载力与GFRP筋抗剪强度呈正相关，与螺纹参数呈负相关，并通过室内钉头锚固性能试验的脆性破坏特点，确定了GFRP筋钉头位置的安全系数在1.8～2.0之间。

3）判定公称外径32 mm的中空GFRP筋釘头安全荷载在125～135 kN之间，大于实际工程中土钉需要承担的极限拉应力，同时证明了此种土钉支护的钉头可以在实际工程中应用。

基于钉头力学模型，为提高钉头极限荷载，除选用高强度材料提高钉头抗剪强度之外，还可降低螺纹参数，如采用梯形螺纹或锯齿形螺纹替代普通螺纹及管螺纹。

参考文献

[1]  刘军， 丁振明， 章良兵. 北京地铁基坑工程设计与施工[M]. 北京： 中国建筑工业出版社， 2016.

LIU J， DING Z M， ZHANG L B. Design and construction for foundation excavation of Beijing metro engineering [M]. Beijing： China Architecture & Building Press， 2016. （in Chinese）

[2]  黄生文， 刘廷望， 邱贤辉， 等. GFRP土钉加固软岩边坡的研究[J]. 土木工程学报， 2012， 45（2）： 90-96.

HUANG S W， LIU T W， QIU X H， et al. A study of weak rock slopes with GFRP soil-nailing [J]. China Civil Engineering Journal， 2012， 45（2）： 90-96. （in Chinese）

[3]  刘伟庆， 方海， 方园. 纤维增强复合材料及其结构研究进展[J]. 建筑结构学报， 2019， 40（4）： 1-16.

LIU W Q， FANG H， FANG Y. Research progress of fiber-reinforced composites and structures [J]. Journal of Building Structures， 2019， 40（4）： 1-16. （in Chinese）

[4]  岳清瑞， 杨勇新. 纤维增强复合材料加固结构耐久性研究综述[J]. 建筑结构学报， 2009， 30（6）： 8-15.

YUE Q R， YANG Y X. Introduction to durability of concrete strengthened with fiber reinforced polymers [J]. Journal of Building Structures， 2009， 30（6）： 8-15. （in Chinese）

[5]  CHENG Y M， CHOI Y K， YEUNG A T， et al. New soil nail material-pilot study of grouted GFRP pipe nails in Korea and Hong Kong [J]. Journal of Materials in Civil Engineering， 2009， 21（3）： 93-102.

[6]  朱鸿鹄， 张诚成， 裴华富， 等. GFRP土钉拉拔特性研究[J]. 岩土工程学报， 2012， 34（10）： 1843-1849.

ZHU H H， ZHANG C C， PEI H F， et al. Pullout mechanism of GFRP soil nails [J]. Chinese Journal of Geotechnical Engineering， 2012， 34（10）： 1843-1849. （in Chinese）

[7]  NATOLI E， ADMIRAAL B， WIT D， et al. River embankment strengthening by non-metallic nails： overview on a permanent soil nailing for flood protection [J]. Innovative Infrastructure Solutions， 2017， 2（1）： 1-10.

[8]  HAMEDMIRJAFARI B， BOLOURI B J， ABRISHAMI S. Experimental investigation of bond stress and creep displacements of GFRP soil nails simulated in a soil box [J]. International Journal of Civil Engineering， 2019， 17（10）： 1559-1570.

[9]  刘毅， 孙涛， 徐开山， 等. 柔性复合材料面层土钉墙支护在基坑工程中的应用[J]. 建筑施工， 2020， 42（4）： 515-517.

LIU Y， SUN T， XU K S， et al. Application of soil nailing wall support with flexible composite surface in foundation pit engineering [J]. Building Construction， 2020， 42（4）： 515-517. （in Chinese）

[10]  柳颂丹. 绿色土钉墙支护结构体系施工工艺及经济性分析[D]. 北京： 北京建筑大学， 2020： 11-14.

LIU S D. Construction technology and economic analysis of green soil nail wall supporting structure system [D]. Beijing： Beijing University of Civil Engineering and Architecture， 2020： 11-14. （in Chinese）

[11]  建筑基坑支護技术规程： JGJ 120—2012 [S]. 北京： 中国建筑工业出版社， 2012.

Technical specification for retaining and protection of building foundation excavations： JGJ 120—2012 [S]. Beijing： China Architecture & Building Press， 2012. （in Chinese）

[12]  黄生文， 邱贤辉， 何唯平， 等. FRP土钉主要性能的试验研究[J]. 土木工程学报， 2007， 40（8）： 74-78.

HUANG S W， QIU X H， HE W P， et al. An experimental study on the performance of FRP soil nails [J]. China Civil Engineering Journal， 2007， 40（8）： 74-78. （in Chinese）

[13]  白晓宇， 张明义， 王永洪， 等. 岩石GFRP抗浮锚杆承载性能室内试验与机理分析[J]. 土木建筑与环境工程， 2018， 40（5）： 78-85.

BAI X Y， ZHANG M Y， WANG Y H， et al. Full-scale test and mechanism analysis on bearing capacity of GFRP anti-floating anchor socketed into rock [J]. Journal of Civil， Architectural & Environmental Engineering， 2018， 40（5）： 78-85. （in Chinese）

[14]  张杰， 叶义成， 邹常富， 等. 玻璃钢锚杆拉拔力测试试验方案研究[J]. 矿业研究与开发， 2013， 33（2）： 49-52， 109.

ZHANG J， YE Y C， ZOU C F， et al. Study on testing scheme of pulling force of GFRP bolt [J]. Mining Research and Development， 2013， 33（2）： 49-52， 109. （in Chinese）

[15]  高洋. 玻璃钢锚杆抗拉强度试验的分析研究[J]. 煤炭科技， 2015（2）： 12-14.

GAO Y. Analytical study of tensile strength test of GFRP anchors [J]. Coal Science & Technology Magazine， 2015（2）： 12-14. （in Chinese）

[16]  何杰， 吴建星. 高强玻璃钢锚杆承载特性及应用研究[J]. 煤炭技术， 2015， 34（12）： 42-44.

HE J， WU J X. Research on bearing behavior and application of high strength FRP bolt [J]. Coal Technology， 2015， 34（12）： 42-44. （in Chinese）

[17]  预应力筋用锚具、夹具和连接器： GB/T 14370—2015 [S]. 北京： 中国标准出版社， 2016.

Anchorage， grip and coupler for prestressing tendons： GB/T 14370—2015 [S]. Beijing： Standards Press of China， 2016. （in Chinese）

[18]  王伸， 李化敏， 李东印， 等. 横肋对螺纹钢树脂锚杆荷载传递的影响[J]. 岩土力学， 2018， 39（8）： 2805-2813， 2822.

WANG S， LI H M， LI D Y， et al. The effect of rib on load transfer of the thread steel resin bolt [J]. Rock and Soil Mechanics， 2018， 39（8）： 2805-2813， 2822. （in Chinese）

[19]  陈佳炜， 熊海贝， 王治方. 正交胶合木-混凝土螺栓连接力学性能试验研究及参数分析[J]. 建筑结构学报， 2021， 42（4）： 203-214， 222.

CHEN J W， XIONG H B， WANG Z F. Experimental study and parametric analysis on mechanical performance of CLT-concrete bolted connection [J]. Journal of Building Structures， 2021， 42（4）： 203-214， 222. （in Chinese）

[20]  颜庭梁， 李家春. 螺纹载荷分布计算方法研究及有限元分析[J]. 机电工程， 2020， 37（5）： 471-477.

YAN T L， LI J C. Calculation method of thread load distribution and finite element analysis [J]. Journal of Mechanical & Electrical Engineering， 2020， 37（5）： 471-477. （in Chinese）

[21]  SOPWITH D. The distribution of load in screw threads [J]. Archive Proceedings of the Institution of Mechanical Engineers， 1948（159）： 373-383.

[22]  YAMAMOTO A. The theory and computation of threads connection [M]. Tokoy： Yokendo， 1980．

[23]  郭平. 機械设计基础[M]. 北京： 北京理工大学出版社， 2017.

GUO P. Basics of mechanical design [M]. Beijing： Beijing Insititute of Technology Press， 2017. （in Chinese）

[24]  孟玲琴， 王志伟. 机械设计基础[M]. 4版. 北京： 北京理工大学出版社， 2017.

MENG L Q， WANG Z W. Basics of mechanical design [M]. 4th ed. Beijing： Beijing Insititute of Technology Press， 2017. （in Chinese）

（编辑  胡玲）