测压管长度对单测点信号的影响及修正效果验证

张亮亮 陈傲 李少鹏 李智扬

DOI： 10.11835/j.issn.2096-6717.2022.007

基金項目：国家自然科学基金（51978108）；“111项目”（B18062）；重庆市教委科学技术研究项目（KJZD-K201905201）

作者简介：张亮亮（1956- ），男，博士，教授，主要从事桥梁与建筑结构抗风研究，E-mail：zll200510@126.com。

通信作者：李少鹏（通信作者），男，教授，博士生导师，E-mail：lishaopeng0314@163.com。

Received： 2021?10?29

Foundation items： National Natural Science Foundation of China （No. 51978108）; 111 Project （No. B18062）; Science and Technology Research Program of Chongqing Municipal Education Commission （No. KJZD-K201905201）

Author brief： ZHANG Liangliang （1956- ）， PhD， professor， main research interests： wind-resistance of bridges and building structures， E-mail： zll200510@126.com.

corresponding author：LI Shaopeng （corresponding author）， professor， doctorial supervisor， E-mail： lishaopeng0314@163.com.

（1. 重庆大学 土木工程学院，重庆 400045； 2. 重庆建筑科技职业学院，重庆 401331）

摘要：测压试验中，测压管的存在会导致风压信号产生畸变，影响后续数据分析的精度。通过实际测定测压管路频响函数，获得测压管对信号的影响规律，并揭示了“B-T理论”的不足。在实际紊流作用下研究测压管长度对单测点压力数据和模型整体力的影响，并验证“B-T理论”的修正效果。结果表明：对于单测点压力数据，测压管将不会影响数据均值和变异系数，标准差随管长增加先增后减，信号时域随管长增加而整体向均值靠近，相位则不断滞后，信号频域值随管长和频率的增加逐渐偏离真实值；对于整体力，整体阻力、各力的相关性、相干性均可认为不受测压管影响，力谱的变化规律与单测点频域值相同；“B-T理论”在信号时域上修正效果较差，在频域修正方面表现良好。

关键词：测压试验；测压管；频响函数；信号修正；紊流

中图分类号：U446.1；TU317     文献标志码：A     文章编号：2096-6717（2024）03-0124-10

Effects of the piezometric tube length on single measuring point signal and the verification of the correction effect

ZHANG Liangliang^1，2， CHEN Ao¹， LI Shaopeng¹， LI Zhiyang¹

（1. School of Civil Engineering， Chongqing University， Chongqing 400045， P. R. China； 2. Chongqing College of Architecture and Technology， Chongqing 401331， P. R. China）

Abstract： In the pressure test， the presence of the piezometric tube will distort the pressure signal and affect the accuracy of the subsequent data analysis. Through the actual measurement of the frequency response function of the measuring system， the influence law of the piezometric tube on the signal is obtained， and the shortcomings of the “B-T theory” are revealed. Based on this， under the actual turbulent flow， the influence of the piezometric tube length on the pressure data of a single measuring point and the total force of the model is studied， and the correction effect of the “B-T theory” is verified. The results show that for single-point pressure data， the piezometric tube will not affect the data mean and variation coefficient， the standard deviation increases first and then decreases as the tube length increases， the signal time domain approaches the mean value as the tube length increases， the phase keeps lagging， and the signal frequency domain value gradually deviates from the true value with the increase of the tube length and frequency. For the overall force of the model， the overall resistance， the correlation and coherence of each force can be regarded as not affected by the piezometric tube， the change rule of the force spectrum is the same as that of the frequency domain value of single measuring point. “B-T theory” has a poor correction effect in the signal time domain， and performs well in the frequency domain correction.

Keywords： pressure measurement experiment； piezometric tube； frequency response function； signal correction； turbulence

测压试验是风洞试验中重要的一部分，需用一定长度的测压管连接模型表面的测压孔与压力传感器。因此，实测得到的风压信号并非模型表面真实的风压信号，而是经测压管干扰后的失真信号。实测信号与真实信号的差异主要表现在两方面：信号能量（幅值）被放大或削弱；信号相位滞后。同时，这种差异会随测压管长度的增加而变大^[1]。目前一些大型测压试验中的测压管长度已达2 m以上，风压信号将发生严重失真。在测压试验中，实测风压信号几乎是后续一切数据分析的基础，如：获取模型的三分力系数、风压系数，整体力的相关性、相干性、力谱等。因此，研究测压管长度对风压信号的影响，以及如何修正失真信号很重要。

针对管路信号畸变的问题，很多学者进行了研究。理论研究方面：Bergh等^[1]基于流体动力学微分方程，提出了测压管路修正的普遍方法（以下简称为“B-T理论”）；基于流体管道耗散模型，周晅毅等^[2-3]研究了串并联管路的理论耗散模型，徐彬彬等^[4]则通过考虑管道输入端流场的影响，对耗散模型进行修正。管路信号改善方面：张亮亮等^[5]通过采用串接毛细管抑制共振峰的方法，改善了系统的频响特性；Halkyard等^[6]使用补偿滤波器对测量信号进行数字滤波，避免了在频域内处理信号；Kay等^[7]验证了数字滤波方法的适用性。影响因素研究方面：Yoshida等^[8]重点研究了管路弯曲点位置和数量对信号的影响；Wang等^[9]研究了测压管长度、内径、厚度、材料、弯曲曲率等对频响函数的影响；He等^[10]研究了管长与压力传感器空腔体积的测量精度对频响函数的影响。实践应用方面：除基础的建筑、桥梁测压修正^[11-12]外，修正理论也被应用于复杂模型中的3D打印管^[13]，以及考虑因素更加全面、细致的航空航天领域^[14-16]。

目前，“B-T理论”仍是人们开展研究的重要基础，也被广泛应用于工程实践中。然而，“B-T理论”自身存在假设条件^[1]与误差^[9-10]，且是在试验室条件下采用单频声波信号验证得出的，其在实际紊流（多频信号）下的适用性及修正效果有待验证；同样，测压管管长作为影响测压试验和频响函数的关键因素，其对真实风压信号的影响目前也缺乏研究。笔者依托重庆大学直流风洞实验室（CQU-1），对测压管路频响函数进行实测并与“B-T理论”进行对比，研究测压管长度对单测点压力数据和模型整体力的影响，并研究了风场特性（紊流度和紊流积分尺度）对信号畸变的影响，验证了“B-T理论”在实际紊流下的修正效果。

1 频响函数

1.1 定义

如图1所示，设输出信号（畸变信号）的时域为，频域为，输入信号（真实信号）的时域为，频域为，则频响函数可表示为 （1）

式中：为快速傅里叶变换。频响函数为复数，其模为幅频函数，即输出输入信号的幅值之比；辐角为相频函数，即输出输入信号的相位之差。由式（1）可知，信号修正可表示为 （2）

式中：为快速傅里叶逆变换。因此，信号修正的关键为获取测压管路的频响函数。

1.2 “B-T理论”

“B-T理论”的频响函数为^[1]（3）

式中： （4a） （4b） （4c）

为圆频率，为频率，Hz；为测压管内部容积，m³；为测压管管长，m；为测压管内部半径，m；为压力传感器内部空腔体积，m³；为压力传感器空腔变形的无量纲增量，取0；为与压力传感器空腔有关的内部空气变化因子，取1.4；为在试验温度（K）和压力（Pa）下的空气比热容比；为声速，m/s；为试验条件下的空气的密度，kg/m³；为空气普朗特数；为动力黏度；为比热容；为导热系数；和分别为零阶和二阶的第一类贝塞尔函数；和分别为双曲正弦函数和双曲余弦函数。

1.3 实测频响函数

参考马文勇等^[17]与陈波等^[18]的测定方法，对试验室测压系统进行频响函数实测。测定采用PSI公司生产的DTC Initium压力信号采集系统，压力传感器型号为ESP-64HD，最高采集频率约1 000 Hz。测压管采用PVC软管，外径约2.0 mm，内径为0.897 9 mm。根据He等的研究^[10]，测压管内径的测量精度对“B-T理论”结果影响较大，故采用注水法进行精准测量，外径则直接采用标牌值。选取长度20 mm的测压管为参考管，假定该测压管信号为“真实信号”。试验时不同长度的测压管均保持拉直状态。本文所有试验的装置、材料均保持一致。

由圖2可知，对于信号幅值（能量）：当管长较短时，测压管对信号低频区域有增强作用，幅频函数整体先上升后下降；随着管长增加，信号增强范围和增幅均减小，逐渐表现为全频域衰减。对于信号相位：相频函数均为下降趋势，即实测信号会滞后于真实信号，且管长越长，滞后越明显。同时，对比“B-T理论”和实测频响函数可以发现：两者在相频函数上吻合较好，但在幅频函数上有一定差距，理论值普遍低于实测值，且管长越短，差异越明显。

根据Bergh等^[1]和Wang等^[9]的研究可知，“B-T理论”（式（3））为理论推导公式，有假设条件，且忽略了测压管材料、管厚等因素的影响，因而与实测频响函数会有一定差异。对于实测频响函数，测压管规格（材料、内径、厚度）、压力传感器型号的改变都会严重影响其精度，因此，不同实验室间很难通用，需重复进行实测。而“B-T理论”对于100 Hz以内的信号修正效果较好，且其只需基本的测压管和压力传感器参数，即可获得管路频响函数，非常利于工程实践应用。因此，选择“B-T理论”进行信号修正，验证其在实际紊流下的修正效果。

2 测压管长度对单测点压力数据的影响

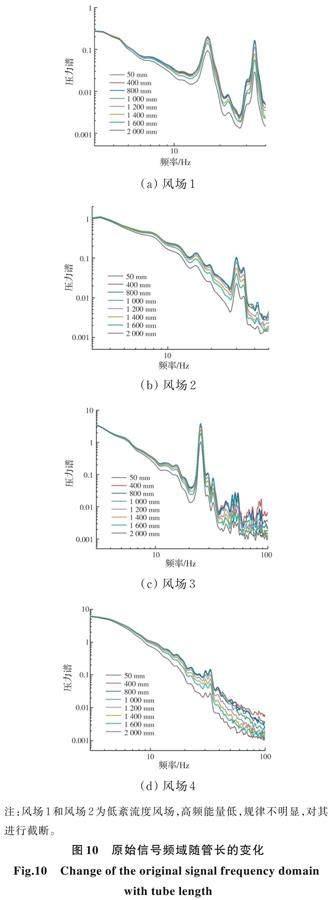
如图3所示，利用分流片（图4），将单测点信号（A0）转化为多通信号（A1、A2…An），分别连接不同长度的测压管，这样可以保证各测压管的输入信号在时域和频域上均是完全相同的，以此来研究测压管长度对单测点压力数据的影响。测压管长度共8种，分别为50、400、800、1 000、1 200、1 400、1 600、2 000 mm，其中50 mm管为参考管，信号经其传播后变化很小，假定为“真实信号”。同时，通过改变风洞格栅类型，形成4种不同纵向紊流度的风场（见表1），以此来研究紊流度对数据的影响。试验时，不同风场下的平均风速保持相同，数据采集频率为250 Hz，每次采集60 s。

2.1 对数据基本数学特征的影响

2.1.1 均值

如图5所示，随着管长增加，均值比整体呈波动式下降，且風场紊流度越大，波动越平缓，但整体误差均在3%以内，满足一般工程要求，可认为管长小于2 m时测压管对压力均值没有影响。由图2可知，各管长的幅频函数起点均为（0，1）点，相频函数起点均为（0，0）点，即理论上测压管只会影响信号的脉动成分，对信号均值（0 Hz）没有影响。实测结果与理论的差异有待进一步深入研究。

2.1.2 标准差

由图6可知，标准差比整体均为先上升，后下降，且大致以1 000 mm为界：当管长小于1 000 mm时，标准差比大于1；当管长大于1 000 mm时，标准差比小于1。这是因为信号的标准差主要受低频区域的影响，如图7所示，假定频域50 Hz以内为影响标准差的主要范围，则可简单认为图中的填充面积为测压管对信号标准差的影响程度，其变化规律与图6相同：填充面积先增后减，大致以1 000 mm管长为界分为放大与衰减作用。同时可以发现，紊流度越小的风场，其标准差受测压管的影响越明显，这也是因为紊流度小的风场低频能量占比高。

2.1.3 变异系数

变异系数=标准差/均值，可以消除不同管长下数据均值不相同的差异，更加客观地反映数据离散程度。如图8所示，变异系数的变化趋势与标准差比（图6）相同，均为先上升后下降，但其变化很小，可认为不随管长变化。同时，其大小与风场紊流度成正相关，这也符合紊流度的定义。

2.2 对信号时域的影响

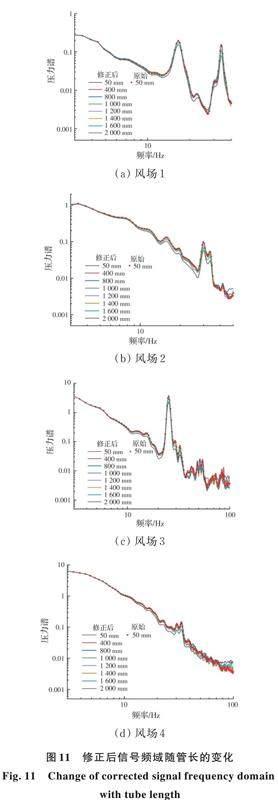
如图9（a）所示，当管长较短时（400 mm），信号的波峰与波谷将被放大，而相位差异不大；随着管长增加，测压管将抑制信号的脉动能量，时域波峰降低，波谷提高，整体向均值（0 Hz）水平线靠近，同时相位不断滞后，表现为信号整体逐渐右移。利用“B-T理论”修正后（图9（b））可以发现，管长较短时修正效果较好，但随着管长的增加，修正后的时域上会新增一些“毛刺”，这表明理论幅频函数是小于真实值的，利用其修正会使一些脉动能量进一步放大；而相位方面，修正后的各管长信号基本与“真实信号”重叠在一起，说明理论相频函数是接近真实值的，这也与图2的结论相吻合。

2.3 对信号频域的影响

由图10可知，随着频率及管长的增加，各管长频域值与“真实信号”的差距会逐渐增大，且风场紊流度越大，差距越明显。但观察发现，当管长小于或等于1 000 mm时，45 Hz以内的信号频域值可认为不受测压管影响。由图11可知，除管长2 000 mm的信号修正有一定偏差外，其余各管长信号修正后基本与“真实信号”重合，说明“B-T理论”在信号频域修正上有很好的效果。

3 测压管长度对模型整体力的影响

在实际测压试验中，模型上会存在多个测点，并通过积分求得模型整体的受力。基于单测点压力数据的研究，探究测压管长度对模型整体力的影响。如图12所示，采用2：1矩形断面模型进行试验，共设两排测点，间距0.07 m，共88个测点。所有测点均连接相同管长的测压管，考虑到实际安装及模型大小的限制，整体管长依次替换为200、400～2 000 mm，共10种。其中200 mm管为参考管，但此时信号受测压管的影响已不可忽略，故不可认作“真实信号”。同样，在4种不同风场（见表2）下进行试验，以此来分析相关风场特性对整体力的影响。由于不同管长的整体力试验不能同时进行，故各管长试验的时域是不相同的，但因为格栅类型和风速保持不变，所以输入信号的频域分布可保证基本相同。试验时，不同风场下的平均风速保持相同，数据采集频率为250 Hz，每次采集120 s。

3.1 对整体力的影响

由于模型为对称截面，风攻角为0°，所以整体升力和力矩值较小，本节选取阻力进行分析。如图13所示，阻力比在1.0附近上下波动，且变化范围均在±3%以内，可认为不受测压管影响。同样，如图14所示，阻力变异系数随管长增加会有一定波动，但变化不大，可以忽略。与图8类似，阻力变异系数与其对应的紊流度I_u成正相关。

3.2 对整体力的相关性的影响

如图15所示，各力的相关性随管长增加有增强趋势，其中力矩的相关性变化明显，升力和阻力变化较小，但均可认为不受测压管影响。同样，各力的相关性与其对应风向的紊流积分尺度成正相关。

3.3 对整体力谱的影响

由图16可知，与单测点试验规律相同，随着管长和频率的增加，力谱逐渐偏离真实值。当管长小于或等于1 000 mm时，45 Hz以内的整体力谱同样可认为不受测压管影响。同时，风场特性（紊流度、紊流积分尺度）对信号畸变没有明显影响，因此图16中不再显示其他风场的情况。由图17可知，修正后各管长的力谱基本为一条曲线，说明“B-T理论”对整体力的频域修正有很好的效果。

3.4 对整体力的相干性的影响

相干函数的定义为^[19]（5）

式中：为频率；为空间两点的距离；（f）为相距的空间两点的互功率谱；（f）、（f）分别为相距的i、j两点各自的自功率谱。由式（2）可知，信号修正的实质是将实测信号的频域除以对应的频响函数，结合式（5）可得式（6）。 （6）

式中：下标“修”表示修正后的结果，下标“原”表示原始数据的结果。

式（6）表明力的相干函数不会受到测压管影响，这与实测结果（图18）相同，各管长的相干函数基本重叠在一起。经“B-T理论”修正后，各相干函数是完全不发生变化的（这里不再显示），也验证了以上结论。

4 结论

针对常见的PVC测压管（直径0.897 9 mm），研究了测压管长度对压力信号的影响及“B-T理论”的修正效果，得到以下主要结论：

1）测压管对信号的影响表现在幅值（能量）与相位上：对于信号幅值，当测压管较短時，其会对信号低频区域有增强作用，而随着管长增加，增强范围和增幅会减小，逐渐表现为全频域衰减；对于信号相位，测压管会导致实测信号滞后于真实信号，且管长越长，滞后越明显。同时，“B-T理论”的幅频函数普遍低于实测值，而相频函数则拟合较好。

2）测压管长度对单测点压力数据的影响：数据均值、变异系数均可认为不受影响，标准差会随管长增加而先增后减；信号时域在管长较短时，波峰波谷会被放大，而随着管长增加，波峰降低，波谷提高，整体向均值水平线靠近，相位则不断滞后；信号频域值随管长和频率的增加，与“真实信号”的差距逐渐增大。

3）测压管长度对模型整体力的影响：整体阻力（均值、变异系数）、各力的相关性、相干性均可认为不受影响；力谱随管长和频率的增加，逐渐偏离真实值。

4）风场特性（紊流度、紊流积分尺度）对管路信号畸变的影响：对于单测点压力数据，风场紊流度越大，均值随管长增加而下降越平缓，标准差受测压管的影响越弱，频域值与真实信号的差异越大，变异系数与紊流度成正相关。对于整体力，阻力变异系数和各力的相关性分别与其对应的紊流度和紊流积分尺度成正相关，而紊流度和紊流积分尺度对整体力谱的畸变没有明显影响。

5）“B-T理论”在信号时域上修正效果较差，会形成多余的“毛刺”，而在频域修正方面表现良好。同时，当测压管长度小于或等于1 000 mm时，45 Hz以内的单测点和整体力的频域值基本不受测压管影响，可不进行修正。

参考文献

[1]  BERGH H， TIJDEMAN H. Theoretical and experimental results for the dynamic response of pressure measuring systems [R]. Amsterdam， The Kingdom of the Netherlands： National Aero and Astronautic Research Institute，1965.

[2]  周晅毅， 顾明. 单通道测压管路系统的优化设计[J]. 同济大学学报（自然科学版）， 2003， 31（7）： 798-802.

ZHOU X Y， GU M. Optimization of dynamic pressure measurement of single-channel tubing systems [J]. Journal of Tongji University， 2003， 31（7）： 798-802. （in Chinese）

[3]  周晅毅， 顾明. 并联管道耗散模型的理论研究[J]. 振动与冲击， 2004， 23（3）： 79-82.

ZHOU X Y， GU M. Research on theoretical representation of dissipative model of parallel tube-manifold systems [J]. Journal of Vibration and Shock， 2004， 23（3）： 79-82. （in Chinese）

[4]  徐彬彬， 王学， 巫朝君， 等. 管道内流动力学修正耗散模型[J]. 航空动力学报， 2021， 36（1）： 78-87.

XU B B， WANG X， WU C J， et al. Improved dissipative model of hydrodynamic in tube [J]. Journal of Aerospace Power， 2021， 36（1）： 78-87. （in Chinese）

[5]  张亮亮， 蒋敏， 张大康. 建筑物表面脉动压力测量与分析[J]. 空气动力学学报， 1996， 14（3）： 288-294.

ZHANG L L， JIANG M， ZHANG D K. Pressure fluctuations on the surface of tall buildings [J]. Acta Aerodynamica Sinica， 1996， 14（3）： 288-294. （in Chinese）

[6]  HALKYARD R， BLANCHARD G， FLAY R， et al. Digital filter adaptation for tubing response correction at reduced sampling frequencies [J]. Journal of Wind Engineering and Industrial Aerodynamics， 2010， 98（12）： 833-842.

[7]  KAY N J， OO N L， GILL M S， et al. Robustness of the digital filter to differing calibration flows [J]. Journal of Wind Engineering and Industrial Aerodynamics， 2020， 197： 104061.

[8]  YOSHIDA A， TAMURA Y， KURITA T. Effects of bends in a tubing system for pressure measurement [J]. Journal of Wind Engineering and Industrial Aerodynamics， 2001， 89（14/15）： 1701-1716.

[9]  WANG X， WANG X N， REN X B， et al. Effects of tube system and data correction for fluctuating pressure test in wind tunnel [J]. Chinese Journal of Aeronautics， 2018， 31（4）： 710-718.

[10]  HE Y C， LIANG Q S， LI Z， et al. Accurate estimation of tube-induced distortion effects on wind pressure measurements [J]. Journal of Wind Engineering and Industrial Aerodynamics， 2019， 188： 260-268.

[11]  李雨航， 鄧扬， 李爱群， 等. 中式高耸古木塔风压分布与体型系数风洞试验研究[J]. 工程力学， 2021， 38（10）： 64-73.

LI Y H， DENG Y， LI A Q， et al. Investigation on wind pressure and shape factor of highrise ancient Chinese wooden pagoda via wind tunnel test [J]. Engineering Mechanics， 2021， 38（10）： 64-73. （in Chinese）

[12]  YAN L， ZHU L D， FLAY R G J. Span-wise correlation of wind-induced fluctuating forces on a motionless flat-box bridge deck [J]. Journal of Wind Engineering and Industrial Aerodynamics， 2016， 156： 115-128.

[13]  KAY N J， OO N L， RICHARDS P J， et al. Characteristics of fluctuating pressure measurement systems utilising lengths of 3D-Printed tubing [J]. Journal of Wind Engineering and Industrial Aerodynamics， 2020， 199： 104121.

[14]  李博， 杨军， 石玉松， 等. 不同校准装置对引压管腔动态特性校准[J]. 航空动力学报， 2019， 34（12）： 2559-2568.

LI B， YANG J， SHI Y S， et al. Calibration of dynamic characteristics of pressure tube cavity by different calibration devices [J]. Journal of Aerospace Power， 2019， 34（12）： 2559-2568. （in Chinese）

[15]  李博， 张鹤宇， 杨军. 不同环境因素对引压管腔动态特性影响[J]. 航空动力学报， 2020， 35（10）： 2159-2165.

LI B， ZHANG H Y， YANG J. Effect of different environmental factors on dynamic characteristics of pressure transmission pipe [J]. Journal of Aerospace Power， 2020， 35（10）： 2159-2165. （in Chinese）

[16]  徐彬彬， 巫朝君， 王学. 管道效应对进气道试验湍流度测量的影响研究[J]. 实验流体力学， 2020， 34（6）： 52-58.

XU B B， WU C J， WANG X. Research on the effect of tubing on turbulence in inlet wind tunnel test [J]. Journal of Experiments in Fluid Mechanics， 2020， 34（6）： 52-58. （in Chinese）

[17]  马文勇， 刘庆宽， 刘小兵， 等. 风洞试验中测压管路信号畸变及修正研究[J]. 实验流体力学， 2013， 27（4）： 71-77.

MA W Y， LIU Q K， LIU X B， et al. Study on correction and distortion effects caused by tubing systems of pressure measurements in wind tunnel [J]. Journal of Experiments in Fluid Mechanics， 2013， 27（4）： 71-77. （in Chinese）

[18]  陈波， 骆盼育， 杨庆山. 测压管道系统频响函数及对风效应的影响[J]. 振动与冲击， 2014， 33（3）： 130-134.

CHEN B， LUO P Y， YANG Q S. Frequency response function of a pressure measurement pipe system and its effect on structural wind effects [J]. Journal of Vibration and Shock， 2014， 33（3）： 130-134. （in Chinese）

[19]  贺德馨. 风工程与工业空气动力学[M]. 北京： 国防工业出版社， 2006.

HE D X. Wind engineering and industrial aerodynamics[M]. Beijing： National Defense Industry Press， 2006. （in Chinese）

（编辑  王秀玲）