基于贝叶斯方法的软土深基坑不确定性位移反演分析

林东 郑俊杰 薛鹏鹏 李子骞 彭荣华

DOI： 10.11835/j.issn.2096-6717.2023.043

收稿日期：2022?10?24

基金项目：中铁第四勘察设计院集团有限公司科研课题（2020K144）

作者简介：林东（1981- ），男，高级工程师，主要从事隧道与地下工程研究，E-mail：004903@crfsdi.com。

通信作者：李子骞（通信作者），男，博士生，E-mail：lizq_97@163.com。

Received： 2022?10?24

Foundation items Scientific Research Items of China Railway SiYuan Group （No. 2020K144）

Author brief： LIN Dong （1981- ）， senior engineer， main research interests： tunnel and underground engineering， E-mail： 004903@crfsdi.com.

corresponding author：LI Ziqian （corresponding author）， PhD candidate， E-mail： lizq_97@163.com.

（1. 中铁四院集团西南勘察设计有限公司，昆明 650206； 2. 华中科技大学 岩土与地下工程研究所，武汉 430074）

摘要：在深基坑开挖工程中，使用合理的土体力学参数计算地连墙侧移对优化基坑支护方案以及降低工程风险至关重要。然而，受地层分布不均、土工试验误差等因素的影响，土体参数常表现出明显的不确定性，该不确定性降低了地连墙侧移计算结果的可信度。鉴于上述问题，提出一种基于贝叶斯参数更新框架和现场监测数据的软土深基坑土体参数反演方法。该方法采用GA-BP神经网络建立数值分析模型中土体参数与地连墙侧移的隐式函数关系，并结合现场监测数据建立土体参数的贝叶斯反分析模型。采用该方法对某深基坑工程进行分析，验证了方法的可行性。分别采用地连墙的最大侧移值和多点位移值作为指标进行土体力学参数反演，并分别使用更新后的土体参数预测基坑开挖的最终侧移值。研究结果表明：与不更新土体参数相比，更新土体参数后土体参数变异系数变小，得到的结果与后续施工步下的监测结果更吻合；使用多点观测值进行土体参数更新的预测效果显著优于仅使用最大位移值时的效果。

关键词：深基坑；土体参数；位移反分析；贝叶斯方法；馬尔科夫链蒙特卡罗模拟

中图分类号：TU753.1     文献标志码：A     文章编号：2096-6717（2024）03-0052-09

Probabilistic method for displacement back analysis of deep excavations in soft soil based on Bayesian method

LIN Dong¹， ZHENG Junjie²， XUE Pengpeng²， LI Ziqian²， PENG Ronghua¹

（1. China Railway SiYuan Group Southwest Survey and Design Co. Ltd.， Kunming 650206， P. R. China； 2. Institute of Geotechnical and Underground Engineering， Huazhong University of Science and Technology， Wuhan 430074， P. R. China）

Abstract： In deep foundation excavation projects， using reasonable soil mechanical parameters to calculate the lateral deformation of diaphragm wall is essential to optimize the support design and reduce engineering risks. However， the soil parameters are generally affected by the uneven distribution and geotechnical testing errors， which often show obvious uncertainties and reduce the credibility of the lateral deformation calculated of diaphragm walls. In view of the considerations above， this paper proposes a back analysis method of soil parameters based on Bayesian parameter updating framework and site monitoring data. This method uses GA-BP neural network to establish the implicit function relationship between the soil parameters and the diaphragm wall lateral displacement in the numerical model， and combines the site monitoring data to establish the Bayesian back analysis model of the soil parameters. This method was used to analyze a deep excavation project， and the feasibility of the method was verified. The maximum lateral displacement and multi-point displacement value of the diaphragm wall were used as indicators to invert the soil mechanical parameters， and the updated soil parameters were used to predict the final lateral displacement. The results show that compared with the non-updating soil parameters， the variation coefficient of soil parameters decreases after updating， and the obtained results fit with the monitoring results better in the subsequent construction steps; the prediction effect of using multi-point observations for soil parameter updating is significantly better than that when only the maximum displacement value is used.

Keywords： deep foundation excavation； soil paraneter； displacement back analysis； Bayesian method； Markov Chain Monte Carlo Simulation （MCMCS）

随着城市发展的加速，城市交通需求随之陡增，地下轨道交通的建设是缓解城市交通压力的重要手段。地铁车站往往选在建筑密集、地下管网交错的区段，对基坑施工过程中的变形控制更加严格。现行的城市软土深基坑主流开挖支护设计多采用地连墙与内支撑联合支护的形式，且将地连墙的水平侧移作为安全预警的控制指标之一。由于基坑工程的邻近区域复杂，且基坑水平向变形的影响因素较多，使用传统力学方法推导解析式来计算基坑中地连墙的水平侧移往往难以实现^[1]。随着计算机技术的发展和各种数值仿真软件的兴起，使用数值模拟技术对基坑进行计算也是现行工程中的常用手段^[2-4]，除了精细的模型和正确的模拟方法外，合理的土体力学参数也是可信计算结果的必要条件之一。事实上，土体参数常常会受不确定性和测量误差的影响产生偏离，直接影响数值仿真模拟结果的可信度^[5]。为了降低土体不确定给工程计算带来的不良影响，学者们提出了多种解决方法，主要分为以下两种：建立土工试验成果与土体力学参数之间的解析式^[6-9]；充分利用现场实测数据，反演计算合理的土体力学参数值 ^[10-14]。

目前已有神经网络^[15]、遗传算法^[16]、粒子群算法^[17]、贝叶斯方法^{[12-14， 18-19]}等算法被用于位移反演分析，其中大部分算法规定目标土体参数为常数，因此，这些方法的反演结果是一系列定值。然而，由于计算模型和观测数据存在误差，上述定值与土体参数的真实值也存在相应的误差。此时，贝叶斯方法的优势便显现出来。贝叶斯方法规定目标土体参数为随机变量而非定值，在土体参数先验估计的基础上，得到土体参数的先验分布，并通过现场监测数据不断修正先验分布以获得更可靠的后验分布，该后验分布综合体现了先验信息和样本信息。

针对确定性反演方法难以得到土体参数统计值的问题，以某软土深基坑为例，提出多点多参数的贝叶斯不确定性反演方法。该方法使用马尔科夫链产生大量样本，并使用蒙特卡罗法对土体参数进行更准确的概率计算。分别以监测数据中的地连墙最大位移值和多点位移观测值进行贝叶斯参数更新，比较在两种参数更新方式下的地连墙水平侧移值。

1 贝叶斯参数更新框架

1.1 基本原理

采用考虑模型误差的贝叶斯参数更新框架。若过分简化计算模型的边界条件、本构模型等要素，在工程计算中普遍存在误差，且计算所得的结构、岩土体响应值与现场实测数据存在一定误差。因此，采用文献[20]中提出的模型偏差因子来表示模型误差。 （1）

式中：表示在深度为处的真实地连墙侧移，下标np为贝叶斯更新中使用的观测点数目。表示深度为处各点的模型偏差因子。采用两种方式进行参数更新：当仅使用地连墙最大实测值进行更新时，取μ_ε=0.905，σ_ε=0.303；当以多点实测值进行更新时，应考虑各点之间的相互影响，各点间的相关系数按参考文献[5]进行取值。表示数值模型计算所得的各个点的地连墙水平位移值。

规定模型偏差因子为对数正态分布，则式（1）可转化为对数形式，即 （2）

由于不考虑模型的誤差变异性，贝叶斯框架的后验概率密度函数可按（3）式表示。 （3）

式中：为参数θ的先验概率密度函数，为避免出现负数，假定为对数正态分布；θ为反演参数；D为位移观测值；k为归一化系数；为似然函数，在使用多点观测数据时，似然函数可表达为 （4）

式中：表示的协方差矩阵的行列式；为观测位移值的对数矩阵；表示的均值矩阵。将（4）式代入（3）式即可求得参数的后验分布。在使用单点最大位移观测数据时，可同样采用上式进行计算似然函数。

取，则，相关系数矩阵需要通过式（5）对文献[5]中的相关系数进行转换得到^[21]。 （5）

式中：为和的相关系数；为和的相关系数；为的标准差；为的标准差。

1.2 马尔科夫链蒙特卡罗模拟

贝叶斯算法框架以联合概率密度函数作为被更新的目标反演参数。而在计算单一的反演参数时，其统计值和边缘分布经常涉及计算困难的高维积分。为解决参数后验分布密度和后验分布统计值的计算问题，学者们提出了Naylor-Smith逼近法^[22]、Lindley数值逼近法^[23]、Tierney-Kadane逼近法^[24]等方法，但这些方法仅在其特定的场景中适用。马尔科夫链蒙特卡罗模拟将马尔科夫链引入蒙特卡罗模拟，使抽样分布随模拟计算的进行而改变，极大改善了蒙克卡罗模拟的高维积分计算效率。因此，马尔科夫链蒙特卡罗模拟作为一种高效、通用的计算方法得到广泛应用^{[14， 20， 25]}。

由于式（3）难以直接求解，通常采用马尔科夫链蒙特卡罗模拟来解决这一问题。其优点是：能够考虑任何类型的先验分布；对观测数据的数量没有严格要求；通过马尔科夫链蒙特卡罗模拟生成的样本可用于后续的分析计算。

马尔科夫链蒙特卡罗模拟的基本思想是构造一条马尔科夫链，并使其收敛为待估参数的后验分布。基于该马尔科夫链可以直接生成后验样本，且在这些样本中每个样本仅与马尔科夫链前一个状态的样本相关，这个性质被称为“马尔科夫性质”。

实现马尔科夫链蒙特卡罗模拟的相关算法有多种，采用Metropolis-Hastings算法，其计算过程如下。

1）约定符号：为当前马尔科夫链样本；为下阶段马尔科夫链样本；为与θ相关的样本ξ的建议概率分布函数；r_k为接受率，按（6）式计算。 （6）

2）产生备选样本，根据马尔科夫链当前样本和建议概率分布函数生成样本。计算当前状态的接受率。

3）从区间[0，1]的均匀分布中抽样出一个随机数u，将随机数u与接受率进行比较，若，则马尔科夫链转移到下个状态；否则马尔科夫链继续保留当前状态。Metropolis-Hastings算法是基于Metropolis算法的改进算法，有效提高了接受率较小时马尔科夫链达到细致平稳的计算效率，其具体实现见文献[13]。

1.3 GA-BP神经网络响应面

重复、大量的岩土体响应计算工作是贝叶斯更新框架中的主要难题之一。若使用传统的有限元法（或有限差分法）进行成千上万次的数值试验，将耗费大量的时间和计算机资源。为了解决这一问题，采用响应面法来提升计算效率。

响应面法通过建立输入参数与岩土体响应之间的关系，用简单的函数关系来代替繁杂的数值模型计算。经过比较选择，采用文献[26]中的遗传算法改进BP神经网络，即GA-BP神经网络，来选择合适的响应面，算法的实现过程如图1所示。由于BP神经网络采用梯度下降算法更新权值与阈值，因此，BP神经网络的计算效率高度依赖权值与阈值的初始值。将遗传算法引入BP神经网络后，可将BP神经网络中的权值与阈值设置为初始染色体，经过选择、交叉、变异等运算后即可获得较为合理的BP神经网络初始权值与阈值。

2 基坑案例数值模拟

2.1 基坑概况

某基坑^[27-29]采用地连墙与内支撑联合支护的设计，基坑的典型剖面、土层分布及支撑设置如图2所示。其中，地连墙厚度为800 mm，埋深为31 m；施工过程分为7个开挖步，各开挖步高程见模拟方案。

2.2 数值模型的建立

1）模型几何尺寸

选取1 m厚的基坑典型断面，并取半结构，采用岩土有限差分软件FLAC^3D建立数值模型，数值模型的几何尺寸为77.5 m×1.0 m×36.0 m。

2）模型参数

土体的本构模型采用摩尔-库伦模型；钢支撑、地连墙的本构模型采用线弹性本构模型。数值模型的具体物理力学参数见表1。

在数值模型中土体、地连墙采用实体单元模拟，钢支撑采用梁单元模拟。模型的边界条件如下：模型底边为固定约束；模型的4个侧面设置法向约束，并约束钢支撑右侧端点的水平位移。模型的网格划分如图3所示。

3）模拟方案

基坑的具体开挖的步骤如下：

①浇筑地连墙与初始地应力平衡，生成初始地应力场；②开挖土体至第一开挖面-1.6 m处；③开挖土体至第2开挖面-4.3 m处，在-1 m处架设支撑；④开挖土体至第3开挖面-6.9 m处，在-3.7 m处架设支撑；⑤开挖土体至第4开挖面-10.15 m处，在-6.2 m处架设支撑；⑥开挖土体至第5开挖面-13.2 m处，在-9.5 m处架设支撑；⑦开挖土体至第6开挖面-16.2 m处，在-12.5 m处架设支撑；⑧开挖土体至第7开挖面-18.45 m处，在-15.5 m处架设支撑。

2.3 地连墙位移的变化规律

图4为数值模拟结果与基坑连续墙侧向位移观测数据对比图。由图可知，在基坑開挖的过程中，连续墙的侧移曲线呈中间大，两端小的分布规律。其中最大水平位移出现在最后一个开挖步，最大侧移值为73.68 mm。整体而言，数值模型的地连墙侧移曲线的变化趋势基本符合现场监测数据，但两者在数值上仍有不可忽视的差距。因此，有必要采用后文中的反分析方法对土参数进行反演分析来获得更合理的结果。鉴于前3开挖步中地连墙侧移观测曲线与后4步侧移观测曲线的差异较大，且从第4开挖步开始地连墙侧移曲线有较为一致的变化趋势，因此，反分析仅从基坑开挖的第4步开始。

3 基于贝叶斯方法的位移反分析

3.1 构建反分析模型

基坑数值模型共涉及4个土层，每个土层从上至下依次编号为1～4。由于土体的弹性模量E具有较大的变异性，往往难以准确测量^[30]，且在使用摩尔-库伦本构模型进行基坑开挖计算时，基坑水平向变形对弹性模量较为敏感^[31]，因此，以弹性模量E为反演目标参数，设计如表2所示的4因素3水平正交试验，并基于该正交试验分别建立多项式响应面和GA-BP神经网络响应面。其中，在多项式响应面中，采用不含交叉项的二次多项式来表示响应面函数，不同深度z_j处的响应面函数可表示为 （7）

式中：b_j，i为多项式函数的待定系数；δ（θ，z_j）表示z_j深度处的响应面函数；θ_i表示第i个参数。

GA-BP神经网络响应面建立方式如下。提取各开挖步相应的地连墙水平位移，基于GAOT工具箱建立位移反分析模型。网络结构为3层神经网络，分别对应输入层、隐层和输出层，各层节点数设置为11、23、4，主要使用trainlm函数训练样本，采用tansig函数作为隐含层的激活函数，采用purelin函数作为输出层的激活函数。设置遗传算法的主要參数为：种群规模P=150，交叉概率P_c=0.24，变异概率P_m=0.04，选择概率P_s=0.09，最大进化代数为100。

3.2 响应面结果分析

使用基坑最终开挖步的监测数据来分别判断多项式响应面和GA-BP神经网络响应面的适用性。

计算100组随机样本下的本基坑数值模型响应。将100组随机样本分为两部分，使用前50组样本训练GA-BP神经网络，使用后50组样本分别评价多项式响应面和神经网络响应面的拟合结果，多项式响应面与GA-BP神经网络响应面和数值模拟的地联墙位移对比见图5。

由图5（a）可见，多项式响应面和数值模拟结果基本上位于45°线（y=x）附近，但是数据点的离散性较大，拟合效果较差；由图5（b）可见，由GA-BP神经网络响应面所得的地连墙位移和由数值模拟所得的地连墙位移基本吻合，拟合度较高。因此，可以选用GA-BP神经网络作为响应面函数。

3.3 贝叶斯更新结果分析

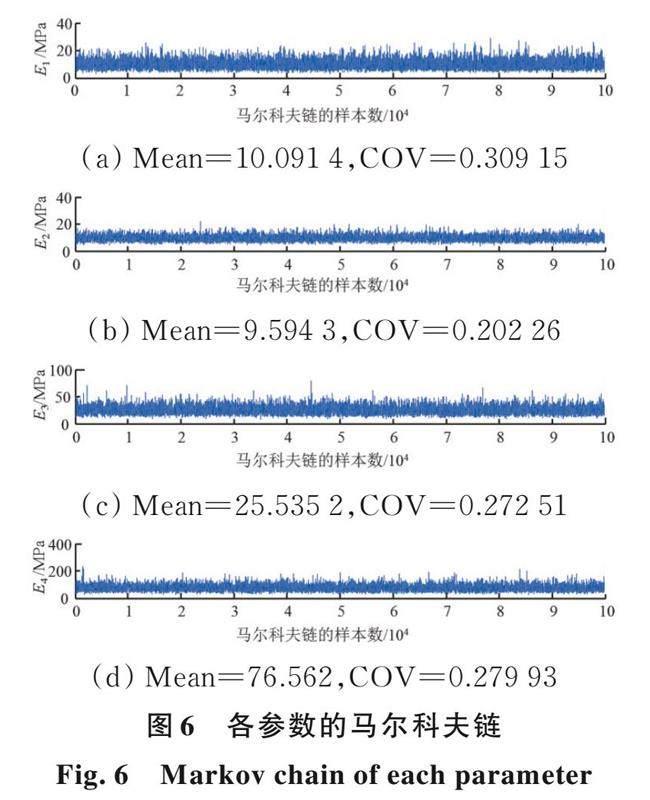
设置马尔科夫链长度为100 000，并取缩放因子为s=1.5，可得如图6所示的第7开挖步下的马尔科夫链样本。通过马尔科夫链的样本统计特征可得到经贝叶斯更新后的土体力学参数信息，第7步开挖中的参数更新结果如图7所示，其中图7纵坐标PDF为概率密度函数（Probability Density Function）的缩写。由图7可见，在引入了现场实测数据更新修正土体参数后，数值积分得到的概率密度曲线与后验分布高度一致，可以认为更新后的土体弹性模量E服从对数正态分布。经贝叶斯更新后，各土层弹性模量E的离散程度均有所减小，验证了贝叶斯参数更新方法的有效性。此外，随着土层自上而下分布，弹性模量E更新前后的差别变大，其中最下层地基土可能由于钻孔勘测数据误差较大等原因，其弹性模量E₄的均值变化最大；而顶层地基土由于其分布位置较浅，对基坑侧移变形的影响有限，其弹性模量E₁更新前后的差别较小。

经过贝叶斯参数更新，基于当前开挖步修正了施工扰动对土体参数的影响。采用更新后的当前开挖步土体参数进行计算，能更准确地预测基坑开挖过程中的地连墙侧移，对施工安全具有重要意义。

若仅从第4步开始进行贝叶斯参数更新，并预测后续各开挖步的地连墙位移，分别采用地连墙最大侧移实测值和多点侧移实测值进行参数更新和位移预测，绘制位移预测结果如图8所示。

以45°线为参照，由图8（a）可知，当仅使用地连墙最大侧移实测值进行更新时，地连墙的位移预测值与现场实测值依然存在较大差异，但该差异随着贝叶斯更新次数的增加而逐渐变小，最终相对误差为5.58%。

图8（b）为采用多点位移观测值进行参数更新的预测结果。从图中可见，在引入地连墙多点水平侧移实测数据进行参数更新后，地连墙的最大侧移预测值与现场实测数据基本吻合，地连墙最终侧移值与实测值的相对误差仅为0.114%。由此可见，使用多点观测数据的更新效果明显好于仅使用最大观测值的更新效果。

4 结论

采用GA-BP神经网络建立了数值模拟中土体参数与地连墙侧移的响应面，并以该响应面方程为基础，提出了基于贝叶斯方法的土体参数反分析方法。最后采用马尔科夫蒙特卡罗模拟方法进行抽样，以台湾某基坑为例讨论了方法的可行性。得出如下主要结论：

1）采用GA-BP神经网络建立的响应面模型是有效的，该响应面代替了贝叶斯参数更新框架中的确定性分析过程，可极大提高贝叶斯反分析计算效率。本文仅考虑了土层弹性模量E的单参数反演，关于考虑多因素的多参数反演分析的合理性和适用性还有待进一步研究。

2）响应面的选择对计算精度有明显影响。建立的多项式响应面和基于GA-BP神经网络的响应面均能合理地表征土体参数与地连墙侧移之间的隐式函数关系。但在样本数目足够时，采用GA-BP神经网络建立的响应面相比多项式响应面具有更好的拟合精度。

3）与不更新土体参数相比，使用该文方法更新土体参数后得到的结果与后续施工步下的监测结果更吻合，在引入监测数据进行参数更新后，更新后的参数变异系数变小，且使用多点观测值进行土体参数更新的预测效果显著优于仅使用最大位移值时的效果。

参考文献

[1]  杨庆年. 武汉地铁车站深基坑变形特性分析[D]. 武汉： 华中科技大学， 2010.

YANG Q N. Analysis of deformation characteristics of deep foundation pit in Wuhan subway station [D]. Wuhan： Huazhong University of Science and Technology， 2010. （in Chinese）

[2]  何忠明， 王盘盘， 王利军， 等. 深基坑施工对临近地铁隧道变形影响及参数敏感性分析[J]. 长安大学学报（自然科学版）， 2022， 42（4）： 63-72.

HE Z M， WANG P P， WANG L J， et al. Influence of deep foundation pit construction on adjacent subway tunnel deformation and parameter sensitivity analysis [J]. Journal of Chang，an University （Natural Science Edition）， 2022， 42（4）： 63-72. （in Chinese）

[3]  倪小东， 王琛， 唐栋华， 等. 软土地区深基坑超大变形预警及诱因分析[J]. 中南大学学报（自然科学版）， 2022， 53（6）： 2245-2254

NI X D， WANG C， TANG D H， et al. Early-warning and inducement analysis of super-large deformation of deep foundation pit on soft soil [J]. Journal of Central South University （Science and Technology）， 2022， 53（6）： 2245-2254 （in Chinese）

[4]  ZENG C F， ZHENG G， ZHOU X F， et al. Behaviours of wall and soil during pre-excavation dewatering under different foundation pit widths [J]. Computers and Geotechnics， 2019， 115： 103169.

[5]  QI X H， ZHOU W H. An efficient probabilistic back-analysis method for braced excavations using wall deflection data at multiple points [J]. Computers and Geotechnics， 2017， 85： 186-198.

[6]  CAO Z J， WANG Y. Bayesian model comparison and characterization of undrained shear strength [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2014， 140（6）： 04014018.

[7]  WU M， CAI G J， LIU L L， et al. Quantitative identification of cutoff wall construction defects using Bayesian approach based on excess pore water pressure [J]. Acta Geotechnica， 2022， 17（6）： 2553-2571.

[8]  LO M K， WEI X， CHIAN S C， et al. Bayesian network prediction of stiffness and shear strength of sand [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2021， 147（5）： 04021020.

[9]  ZHAO Z N， DUAN W， CAI G J， et al. CPT-based fully probabilistic seismic liquefaction potential assessment to reduce uncertainty： Integrating XGBoost algorithm with Bayesian theorem [J]. Computers and Geotechnics， 2022， 149： 104868.

[10]  FINNO R J， CALVELLO M. Supported excavations： Observational method and inverse modeling [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2005， 131（7）： 826-836.

[11]  章潤红. 考虑黏土各向异性的深基坑开挖响应及其参数反分析研究[D]. 重庆： 重庆大学， 2021.

ZHANG R H. Study on excavation response and parameter back analysis of deep foundation pit considering clay anisotropy [D]. Chongqing： Chongqing University， 2021. （in Chinese）

[12]  仉文岗， 顾鑫， 刘汉龙， 等. 基于贝叶斯更新的非饱和土坡参数概率反演及变形预测[J]. 岩土力学， 2022， 43（4）： 1112-1122.

ZHANG W G， GU X， LIU H L， et al. Probabilistic back analysis of soil parameters and displacement prediction of unsaturated slopes using Bayesian updating [J]. Rock and Soil Mechanics， 2022， 43（4）： 1112-1122. （in Chinese）

[13]  ZHANG W G， GOH A T C， ZHANG Y M. Updating soil parameters using spreadsheet method for predicting wall deflections in braced excavations [J]. Geotechnical and Geological Engineering， 2015， 33（6）： 1489-1498.

[14]  HSEIN JUANG C， LUO Z， ATAMTURKTUR S， et al. Bayesian updating of soil parameters for braced excavations using field observations [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2013， 139（3）： 395-406.

[15]  周小棚， 許强， 赵宽耀， 等. 基于神经网络的离散元细观参数标定方法研究： 以甘肃黑方台黄土滑坡为例[J]. 岩石力学与工程学报， 2020， 39（Sup1）： 2837-2847.

ZHOU X P， XU Q， ZHAO K Y， et al. Research on calibration method of discrete element mesoscopic parameters based on neural network landslide in Heifangtai， Gansu as an example [J]. Chinese Journal of Rock Mechanics and Engineering， 2020， 39（Sup1）： 2837-2847. （in Chinese）

[16]  于京池， 金爱云， 潘坚文， 等. 基于GA-BP神经网络的拱坝地震易损性分析[J]. 清华大学学报（自然科学版）， 2022， 62（8）： 1321-1329.

YU J C， JIN A Y， PAN J W， et al. Seismic vulnerability analysis of arch dam based on GA-BP neural network [J]. Journal of Tsinghua University （Science and Technology）， 2022， 62（8）： 1321-1329. （in Chinese）

[17]  杨道学， 赵奎， 曾鹏， 等. 基于粒子群优化算法的未知波速声发射定位数值模拟[J]. 岩土力学， 2019， 40（Sup1）： 494-502.

YANG D X， ZHAO K， ZENG P， et al. Numerical simulation of unknown wave velocity acoustic emission localization based on particle swarm optimization algorithm [J]. Rock and Soil Mechanics， 2019， 40（Sup1）： 494-502. （in Chinese）

[18]  张雪萍， 彭珍瑞， 张亚峰. 基于Kriging模型和改进MCMC算法的随机有限元模型修正[J]. 计算力学学报， 2021， 38（6）： 712-721

ZHANG X P， PENG Z R， ZHANG Y F. Stochastic finite element model updating based on Kriging model and improved MCMC algorithm [J]. Chinese Journal of Computational Mechanics， 2021， 38（6）： 712-721 （in Chinese）

[19]  张湾， 李典庆， 曹子君. 基坑开挖参数反分析贝叶斯方法比较研究[J]. 武汉大学学报（工学版）， 2016， 49（6）： 806-811

ZHANG W， LI D Q， CAO Z J. Comparative study of Bayesian methods for back analysis of deep excavation [J]. Engineering Journal of Wuhan University， 2016， 49（6）： 806-811 （in Chinese）

[20]  ZHANG J， TANG W H， ZHANG L M， et al. Characterising geotechnical model uncertainty by hybrid Markov Chain Monte Carlo simulation [J]. Computers and Geotechnics， 2012， 43： 26-36.

[21]  PHOON K K， SANTOSO A， QUEK S T. Probabilistic analysis of soil-water characteristic curves [J]. Journal of Geotechnical and Geoenvironmental Engineering， 2010， 136（3）： 445-455.

[22]  NAYLOR J C， SMITH A F M. Applications of a method for the efficient computation of posterior distributions [J]. Applied Statistics， 1982， 31（3）： 214.

[23]  LINDLEY D V. “Approximate Bayesian methods” in Bayesian Statistics [M]. Valencia， Spain： Valencia Press， 1980.

[24]  TIERNEY L， KADANE J B. Accurate approximations for posterior moments and marginal densities [J]. Journal of the American Statistical Association， 1986， 81（393）： 82-86.

[25]  曹子君， 赵腾远， 王宇， 等. 基于贝叶斯等效样本的土体杨氏模量的统计特征确定方法[J]. 防灾减灾工程学报， 2015， 35（5）： 581-585.

CAO Z J， ZHAO T Y， WANG Y， et al. Method for determining statistical characteristics of Youngs modulus of soil based on Bayesian equivalent samples [J]. Journal of Disaster Prevention and Mitigation Engineering， 2015， 35（5）： 581-585. （in Chinese）

[26]  劉春艳， 凌建春， 寇林元， 等. GA-BP神经网络与BP神经网络性能比较[J]. 中国卫生统计， 2013， 30（2）： 173-176， 181.

LIU C Y， LING J C， KOU L Y， et al. Performance comparison between GA-BP neural network and BP neural network [J]. Chinese Journal of Health Statistics， 2013， 30（2）： 173-176， 181. （in Chinese）

[27]  OU C Y， HSIEH P G， CHIOU D C. Characteristics of ground surface settlement during excavation [J]. Canadian Geotechnical Journal， 1993， 30（5）： 758-767.

[28]  XUAN F， XIA X H， WANG J H. The application of a small strain model in excavations [J]. Journal of Shanghai Jiaotong University （Science）， 2009， 14（4）： 418-422.

[29]  TANG Y G， KUNG G T C. Application of nonlinear optimization technique to back analyses of deep excavation [J]. Computers and Geotechnics， 2009， 36（1/2）： 276-290.

[30]  何军涛， 张洁， 黄宏伟， 等. 基于多重响应面法的基坑位移反分析[J]. 岩土力学， 2012， 33（12）： 3810-3817

HE J T， ZHANG J， HUANG H W， et al. Back analysis of displacements of excavation based on multiple response surface method [J]. Rock and Soil Mechanics， 2012， 33（12）： 3810-3817 （in Chinese）

[31]  徐伟， 李靖祺， 段朝静. 某特殊平面形状深基坑围护结构对土层参数敏感性分析[J]. 岩土工程学报， 2010， 32（Sup1）： 173-176.

XU W， LI J Q， DUAN C J， et al. Sensitivity analysis of a deep foundation pit with special plane shape to soil parameters[J]. Chinese Journal of Geotechnical Engineering， 2010， 32（Sup1）： 173-176. （in Chinese）

（编辑  胡玲）