“数据的分析”易错点剖析
毕燕
“数据的分析”这章内容虽然简单,但由于涉及数据较多,同学们在解题时常因为概念不清或者计算马虎而出现错误,本文通过错解展示,对相关的错误进行剖析,希望能让大家引以为戒.
一、求平均数忽视“权”
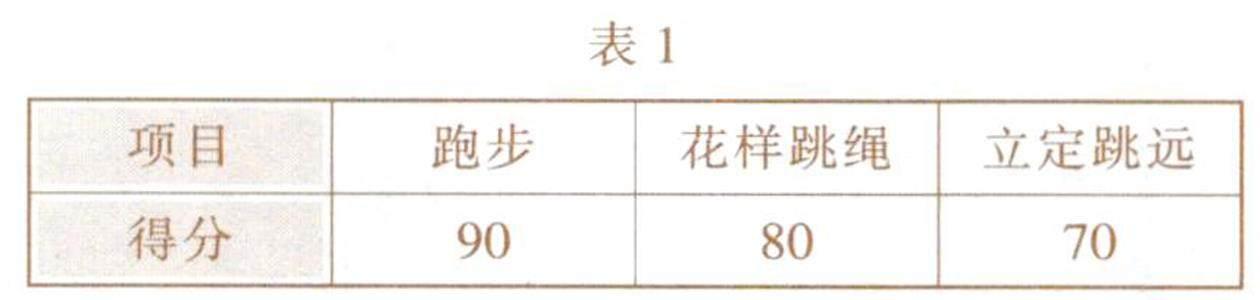
例1 表1是小红参加学校期末体育考核的得分(百分制)情况.评总分时,按跑步占50%,花样跳绳占30%,立定跳远占20%进行计算,则小红的总分(百分制)为________.
错解1:因为小红跑步、花样跳绳和立定跳远的得分分别是90,80,70,所以总分是(90+80+70)÷3=80,故答案是80.
错解2:小红的总分是90+80+70=240.故答案是240.
剖析:错解1忽视了计算总分时,跑步、花样跳绳和立定跳远三项得分的比重是不同的,错将90,80,70的算术平均数80当作总分;错解2直接把90,80,70的和240作为总分,不符合题意要求.出现此类错误的原因,都是忽视了求平均数时“权”的作用.
正解:小红的总分为90×50%+80×30%+70×20%=83,故答案是83.
二、求中位数时未考虑全部数据
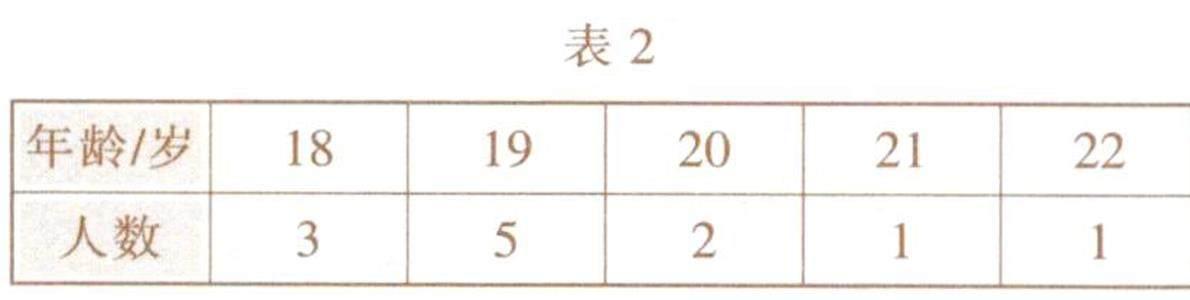
例2 某青年排球队有12名队员,他们年龄的情况如表2所示.
则这12名队员年龄数据的中位数是________.
错解:由统计表可以看出,青年排球队队员的年龄(单位:岁)分别是18,19,20,21,22.其中,20处于最中间位置,所以这组数据的中位数是20.
剖析:错解把18,19,20,21,22这5个数的中位数错误地认为是这12名队员年龄的中位数,出现错误的原因是没有对这12名队员的全部年龄进行排序.
正解:将这12名队员的年龄(单位:岁)按照从小到大排列:18,18,18,19,19,19,19,19,20,20,21,22.处于最中间位置的两个数都是19,所以中位数是19.
三、错将频数当众数
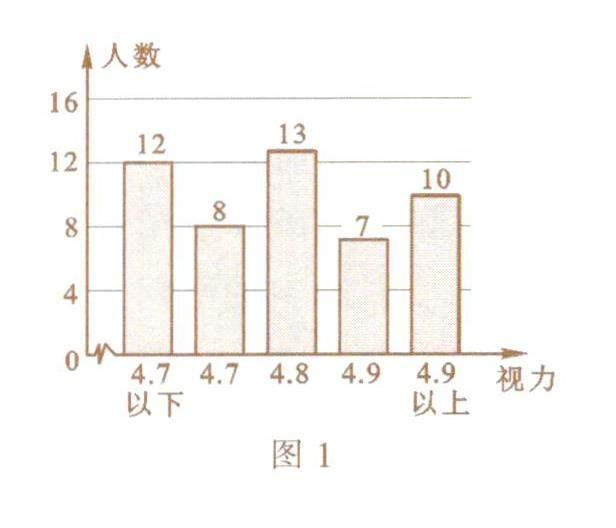
例3 为了解全市中学生的视力情况,随机抽取某校50名学生的视力作为一个样本,整理样本数据如图1所示.则这50名学生视力的中位数和众数分别是( ).
A.4.8,4.8 B.13,13
C.4.7.13 D.4.8,13
错解:把这50名学生的视力从小到大排列,排在最中间的第25和第26两名学生的视力均为4.8.所以中位数是4.8.由统计图可以看出,4.8出现了13次,其次数最多,所以众数为13.选D.
剖析:出现错误的原因是对众数概念理解不透,众数是指出现次数最多的那个数据,而不是数据出现的次数,一组数据的众数一定是该组数据中的“数据”.
正解:把这50名学生的视力从小到大排列,排在最中间的第25和第26两名学生的视力均为4.8,所以中位数是4.8.在这50名学生的视力中,4.8出现了13次,出现次数最多,所以众数为4.8.选A.
四、误认为方差越小越好
例4 学校要从甲、乙两个跳远运动员中挑选一人参加市里举办的跳远比赛.在最近的10次选拔赛中,他們的成绩(单位:cm)如下.
甲:585.596,610,598,612,597,604,600,613.601.
乙:613,618,580,574,618,593,585,590,598.624.
(1)两组数据的平均数和方差各是多少?
(2)历届比赛成绩表明,成绩达到6.10m就能打破纪录,为了打破纪录,你认为应选谁参加这项比赛?
错解:(1)甲成绩的平均数为601.6,乙成绩的平均数为599.3;甲成绩的方差为65.84,乙成绩的方差为284.21.
(2)因为x甲>x乙,s2甲<s2乙,所以甲的平均成绩更好一些,且成绩更稳定,所以因派甲参赛.
剖析:上解错在第2问,虽然乙成绩的平均数小于甲,但在10次选拔赛中,甲达到6.10m的有3次,并且均比较接近6.10m;而乙有4次达到6.10m.且数值较大,又因乙成绩的方差较大,说明乙潜力更大,因此派乙参赛更有希望打破纪录.
正解:(1)甲成绩的平均数为601.6,乙成绩的平均数为599.3:甲成绩的方差为65.84.乙成绩的方差为284.21.
(2)10次选拔赛中,甲达到6.10m的有3次,并且均比较接近6.10m;而乙有4次达到6.10m,且数值较大.所以为了打破纪录,应派乙参赛.
- 中学生数理化·八年级数学人教版的其它文章
- “数据的分析”易错题专练
- “数据的波动程度”专项突破
- “数据的集中趋势”知识演练
- “数据的分析”新题总动员
- 当当闯关记
- 自律带来自由

