聚焦“三数”问题 辨析“三数”特征
赵扩海


尽管平均数、中位数、众数都刻画了数据的集中趋势,但它们各有千秋,能够从不同的角度提供信息,因此有着不同的适用范围.
二 中位数
中位数是一组数据的中间量,代表了该组数据的中等水平.把数据按从小到大(或按从大到小)的顺序排列,位于最中间的一个数(数据总个数为奇数时)或中间两个数的平均数(数据总个数为偶数时)为这组数据的中位数.如果一组数据相差较大,那么用中位数表示这组数据的集中趋势往往更有意义.
例3 为更好地学习贯彻第十四届全国人大一次会议精神,牢记使命担当,奋进新时代,筑梦新征程,某校举办了“第十四届全国人大一次会议”知识竞赛,某班参赛的6名同学的成绩(单位:分)分别为82,84,85,87,88,90,则这组数据的中位数是( ).
A.84 B.85.5 C.86 D.86.5
解析:将这组数据按从小到大的顺序排列,为82,84,85,87,88,90,處于中间位置的两个数是85和87.所以,这组数据的中位数是85+87/2=86,故选C.
三 众数
众数代表的是一组数据的多数水平,众数出现的次数越多,它就越能代表这组数据的整体状况.众数与各个数据出现的频数有关,不受个别数据的影响.注意,一组数据的众数可能不止一个.
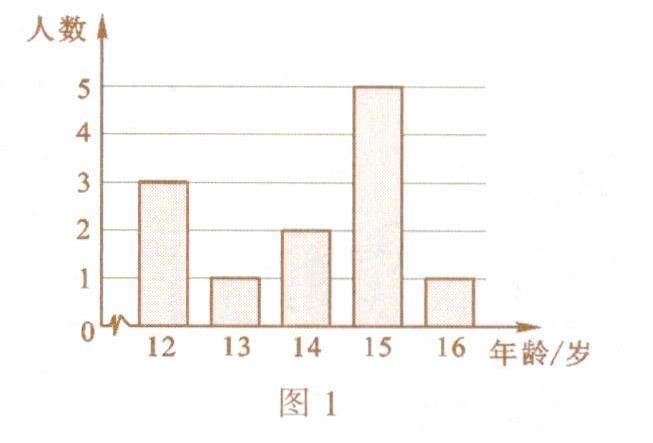
例4 某学校女子排球队12名队员的年龄分布如图1所示,则这12名队员的年龄的众数是( ).
解析:在12名队员的年龄中.15岁的有5人,人数最多,所以众数是15.选D.
例5 表2是某公司15名员工一个月内的销售业绩.
(1)计算这15名员工销售额的平均数、中位数和众数.
(2)为了调动大家的积极性,公司准备制定奖惩制度,对完成目标任务的员工进行奖励,对未完成目标任务的员工进行处罚,那么公司在制定目标任务时,应参考上述统计量中的哪个量?
解析:(1)15名员工销售额的平均数为(300+80×3+50×7+40x2+25+10)/15=67.将15个数据按从大到小排列后,处于中间的数据为50,所以中位数为50.这15个数据中50出现7次,出现次数最多,所以众数是50.
(2)如果以平均销售额67万元为目标任务,则大多数人无法完成任务,会降低员工的积极性.而参考中位数或众数制定目标任务,则能使大多数人得到奖励,可大大提高员工的积极性.
平均数、中位数、众数都是描述数据的集中趋势的“特征数”,它们的适用范围可以总结为:比较接近选平均数,相差较大看中位数,频数较大用众数.
试金石
1.某同学在求15个数的平均数时,错将其中一个数据15写成了45,那么由此求得的平均数与实际平均数的差是( ).
A.2 B.3 C.5 D.-3
2.若数据2,3,4,5,6,x有唯一众数,且其平均数等于众数,则x的值为( ).
A.2 B.3 C.4 D.5
3.两组数据3,x,2y,5与x,6,y的平均数都是6.若将这两组数据合并为一组新数据,则这组新数据的众数为________.
(参考答案在本期找)
- 中学生数理化·八年级数学人教版的其它文章
- “数据的分析”易错题专练
- “数据的波动程度”专项突破
- “数据的集中趋势”知识演练
- “数据的分析”新题总动员
- 当当闯关记
- 自律带来自由

