矿井带式输送机液压拉紧Fuzzy-PID 控制技术研究

王伟峰 ，杨 泽 ，赵轩冲 ，纪晓涵 ，贵晓云 ，何 地

（西安科技大学 安全科学与工程学院, 陕西 西安 710054）

0 引 言

带式输送机是煤矿生产中至关重要的运输生产设备。随着我国的经济与运输发展，对带式输送机的功率和运输距离提出了更高的要求，主要表现在输送带张力变化方面。当带式输送机发生张力突变时会影响到输送机的各个部件，对零件会造成一定程度的磨损，以及消耗大量不必要的能量。当张力超出正常范围后，过大时会严重磨损输送带，甚至断裂。过小时造成输送带打滑，降低运输效率[1–5]。因此，改善带式输送机拉紧系统的响应速度、稳定性，对张力突变进行实时有效的智能控制，对延长带式输送机使用寿命、降低煤矿安全隐患以及提高生产效率等具有重要意义。

2021 年，郭振华[6]从带式输送机制动系统方面进行了优化研究，提高了输送机的运输效率。2022 年，梁国华[7]针对其带式输送机自动化程度低、始终恒速运行浪费能源等问题做出了整体优化，利用各类传感器结合反馈信号来进行调节，以此来提高自动化控制。2023 年，冯晋姣[8]通过改进BP 神经网络结合PID 控制器以此来提高带式输送机运输效率。

传统的带式输送机大多是由PID 控制器进行控制以此来调节张力，但对输送带拉紧进行控制时，PID 控制参数一直保持不变。当带式输送机运行时张力发生变化无法做出对应的调节，会出现输送带拉紧张力无法及时达到期望张力值[9–10]，以及超调量变大等问题。因此，为实现对带式输送机拉紧张力变化的自适应控制，改善PID 控制器的缺陷，在PID控制器的基础上加入了动态响应好的模糊控制，设计了基于模糊PID 控制的液压拉紧控制算法来实现对KP，KI，KD参数的实时优化，从而实现拉紧装置更好的控制效果。并用Simulink 分别对模糊PID 控制器进行仿真并与传统PID 控制器仿真的结果进行对比。

1 带式输送机液压拉紧系统

1.1 液压拉紧系统结构及工作原理

图1 为液压拉紧系统结构原理图[11]。在启动阶段，电控箱先发出启动信号，电机带动定量泵产生压力，通过溢流阀来限制张力上限；蓄能器用来缓冲输送带张力波动；运行阶段，电控系统控制装置的拉紧力，通过采集拉力传感器的数据，判断所需张力来产生给定张力；压力继电器用来控制张紧力在合理范围内；电控部分主要是电控箱，它是整个装置的关键部件，工作原理为：PLC 等待接收上位机的启停等控制信号，PLC 根据接收到的控制信号以及钢丝绳上采集的拉力信号，以此来推断绞车是正转还是反转。

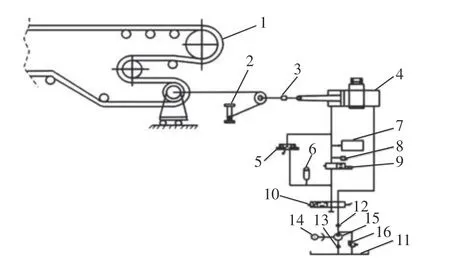
图1 液压拉紧装置系统结构原理Fig.1 Schematic of hydraulic tensioner system structure

液压拉紧系统工作原理：由固定在液压杆和传动滑轮之间的高精度力传感器对输送带进行张力的实时监测，将监测到的输送带张力值对比初设张力值的偏差输出对应电信号，通过力变换器将电信号转化为脉冲信号后发送给控制器。控制器通过逻辑判断带式输送机状态情况发送出相应指令，经驱动电源电路继电器及驱动磁力电路启动器将其传送到拉紧装置的驱动电机，控制电机对其做出驱动状态判断响应，实现对拉紧装置的实时自动控制。

1.2 液压装置输送带拉紧的数学模型

增量封闭式阀的线性化应用流量控制方程

其中，Kq为流量增益，(m3·s-1)/m;Xv为阀芯位移量，m;Kc为流量压力系数，(m3·s-1)/Pa；Pl为液压缸内压力，MPa。

液压缸的流量连续方程：

式中，Ap为进油腔活塞有效面积，m2；βe为有效体积弹性模量，Pa；Cip、Cep为液压缸内、外泄漏系数，(m3·s-1)/Pa；xp为活塞位移，m；Vt为进油腔容量，m3。

液压缸输出力的增量方程：

式中，Fg为液压缸输出力，kN；M为等效总质量，kg ；Bp为黏性阻尼系数；K为负载弹簧刚度，kN/m；Fz为拉紧小车摩擦力，kN。

将式(1)、式(3)函数进行拉氏变换，并对拉氏函数推导计算求得传递函数：

由于黏性阻尼系数Bp很小，可忽略不计，则式(4)整理简化得：

液压固有频率:

弹簧刚度：

由此，建立的液压装置输送带拉紧控制的传递函数方框图如图2 所示：

图2 液压拉紧控制传递函数框Fig.2 Block of the transfer function of hydraulic tensioning control

图2 中，Ka为放大器增益；Ksv为驱动伺服阀拉紧驱动器的增益；Gsv(s)为拉紧驱动器的伺服阀传递函数。

2 Fuzzy-PID 控制技术研究

2.1 Fuzzy-PID 控制器

模糊PID 控制，即利用模糊理论来逐步精确的缩小期望值与实际输出值误差，对PID 控制参数进行在线实时调节，使KP,KI,KD的参数值达到最优，从而实现对被控对象的自适应控制，达到对PID 控制器实时的改善。Fuzzy-PID 控制器如图3 所示[12–15]。

图3 模糊PID 控制原理Fig.3 Fuzzy PID control schematic

2.2 Fuzzy 模糊算法理论结构及计算步骤

从图4 可以看出模糊控制器的4 个计算步骤如下[16–22]：

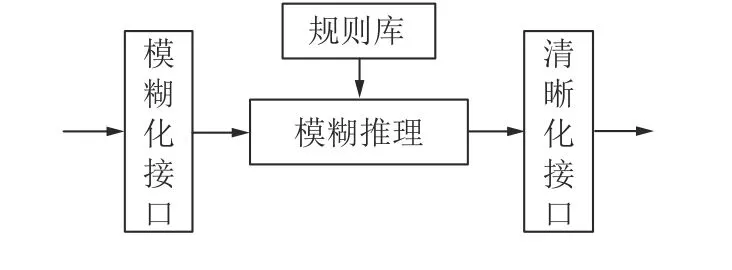
图4 模糊理论结构Fig.4 Fuzzy theoretical structure

1)模糊化接口：把实际的物理值经过模糊化转化到对应的模糊子集。语言变量的确定是对每个输入输出变量各自定义，一般输入选取系统误差值和误差变化率。输出为u。分别为它们自定义论域，为了方便快速查询，制定模糊查询表。最后在定义各语言值的隶属度函数。

2)规则库是基于输入的模糊控制量而来的，是实现模糊推理的基础。它的设定多半依据经验来完成，表现形式多样，可以考虑到的使用方便来制定。

3)模糊推理该模块为模糊控制的核心，利用模糊推理运算，和规则库中的信息，模拟人的推测方法，在输入条件下根据相应的规则给出适当的模糊控制输出。

4)清晰化即解模糊，文中所采取的是平均最大隶属度法。

输入变量模糊化：

张力偏差e={NB,NM,NS,ZO,PS,PM,PB}

张力偏差变化ec={NB,NM,NS,ZO,PS,PM,PB }

将张力偏差e和张力偏差变化率ec分别划分成7 个模糊集{NB,NM,NS,ZO,PS，PM,PB}。上述括号里各元素依次表示为负大，负中，负小,零,正小,正中,正大,它们分别表示[–3,3] 内的7 个整数分别为{–3,–2,–1,0,1,2,3},其中例如“负大”表示为张力偏差或偏差变化率远低于标准值。通过量化函数来确定e和ec对应的模糊子集(为了使得e和ec的精确值和模糊子集对应上，所以引入量化函数)。该式子如下所示：

隶属度函数选取：三角隶属度函数如下所示。

模糊规则：模糊PID 控制器输出的变量是PID的3 个参数，与输入变量论域统一，将各分量的论域映射为7 个数，量化级依次为[–0.3,0.3],[–3,3],[–0.6,0.6],每个语言值的模糊集合的定义如下：比例系数KP={NB,NM,NS,ZO,PS,PM,PB}，积分时间常数KI={NB,NM,NS,ZO,PS,PM,PB}，微 分 时 间 常 数KD={NB,NM,NS,ZO,PS,PM,PB}，见表1、2、3。

表1 ΔKP模糊规则Table 1 Fuzzy rules

根据3 个参数KP,KI,KD对液压拉紧系统输出特性的影响情况，KP,KI,KD参数调节规则如下：

解模糊：所用到的方法为平均最大隶属度法，顾名思义即每次最大的隶属度所对应的值求和取平均。最后经过模糊控制器得出模糊推理，反馈情况给出调整量ΔKP,ΔKI,ΔKD，PID 修正的参数如下：

3 带式输送机液压拉紧系统仿真

结合液压拉紧装置相关参数(表4，对系统影响很小的极点和零点忽略)，对模糊算法PID 控制的参数进行赋值，将开环传递函数即液压拉紧装置控制系统被控对象整理简化为

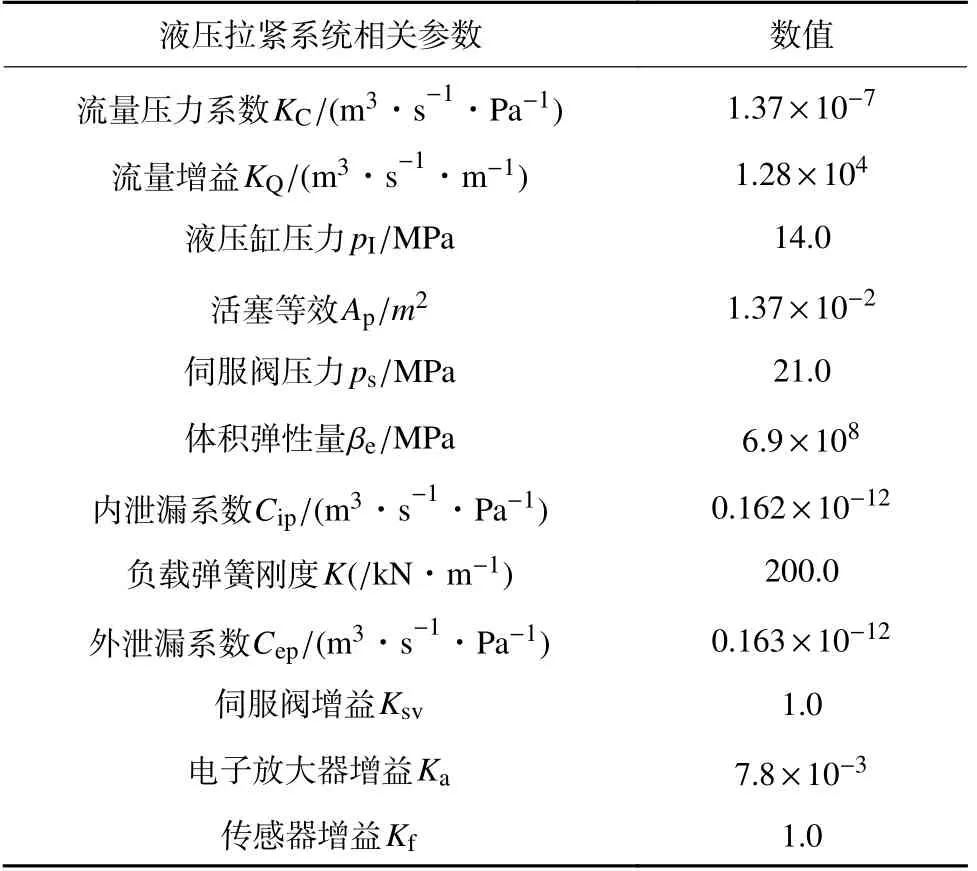
表4 液压拉紧系统相关参数Table 4 Hydraulic tensioning system related parameter

仿真环境：Simulink 提供了仿真、自动代码生成等功能。自定义的模块库或者控制器，可以进行动态系统建模仿真。但Simulink 里只能运算一些简单的运算，所以涉及到一些复杂的运算时还得调用Matlab 里的算法去融入模型。

在这次设计中，模糊PID 算法是利用了Matlab 的fis 文件自定义的模糊规则部署Simulink 的fuzzy logic controller。最后利用Simulink 提供的图形界面对液压拉紧系统建模得出仿真结果。如图5 和图6 就是在Simulink 仿真库里面建造的控制器仿真模型。

图5 基于PID 控制的仿真模型Fig.5 Simulation model based on PID control

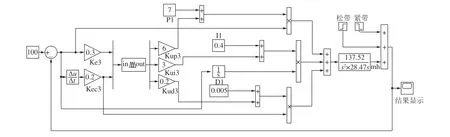
图6 基于模糊PID 控制器的仿真模型Fig.6 Simulation model based on fuzzy PID controller

在这里统一将期望值设为100 张力，通过期望值与实际值得出的误差来继续运行这个闭环模块，直至误差最小。

图7 为PID 控制器仿真结果，紫色表示输送带张力设定的期望值，橙色表示在传统PID 控制器控制下的响应曲线过程。图8 中，黑色代表Fuzzy-PID控制器下的响应曲线过程。

图7 PID 仿真结果Fig.7 PID simulation results

图8 模糊PID 仿真结果Fig.8 Fuzzy PID simulation result plot

由图7 可看出当1.2 s 后张力以达到期望值，而在0～0.4 s 时张力调节速度过快而导致大于期望值，超调量为20%，到达稳定时间为1.2 s。

由图8 仿真结果可以看出，在0.7 s 以后曲线基本达到期望值，超调量为6.5%，并且超调量相对于PID 也降低下来了，之后一直趋于平稳。

为模拟液压拉紧系统张力突变，采用2 种不同控制器对输送带进行紧带和松带的过程，分别在不同时刻改变张力值，即给它的仿真模型中加入阶跃信号，以模拟输送带松带与紧带过程，仿真响应曲线图如图9 所示。其中紫色曲线表示对输送带张力的期望值，橙色曲线表示在传统PID 控制下的响应曲线。

图9 PID 张力突变调节响应Fig.9 PID tension mutation regulation response

如图9 所示，在t=1.5 s 时刻，对张力增加20 N 后，PID 控制器经过0.7 s 使拉紧系统张力再次到达稳定值，超调量为6%。在t=2.5 s 时刻，对张力减少10 N 后，PID 控制器经过0.6 s 使拉紧系统张力再次达到稳定值，超调量为4%。

如图10 所示，与PID 相同，在t=1.5 s 时刻，对张力增加20 N 后，Fuzzy-PID 控制器经过0.3 s 使拉紧系统张力再次到达稳定值，超调量为2%。在t=2.5 s时刻，对张力减少10 N 后，Fuzzy-PID 控制器经过0.3 s使拉紧系统张力再次达到稳定值，超调量为2%。

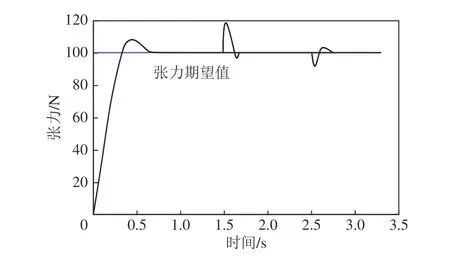
图10 Fuzzy-PID 张力突变调节响应Fig.10 Fuzzy-PID tension mutation regulation response

4 试验分析

鉴于矿井下现场试验测试存在一定的困难，本次采取在实验室里进行试验分析，试验布置如下：①根据带式输送机基本结构在实验室内搭建小型模拟平台。②分别用PID 控制和Fuzzy-PID 控制实施10 次正常启动，用拉力传感器来测量拉力，记录每次到达期望值的时间，这里拉力期望值定为100。③分别运行1 h，记录PID 控制与Fuzzy-PID 控制控制后的电耗，以及电机温度。启动响应试验结果如图11所示。

图11 启动响应时间试验结果对比Fig.11 Comparison of start-up response time experiments

如图11 所示，采用Fuzzy-PID 控制以后，对比于PID 控制，前者控制效果更为良好，且每次启动响应时间更快，平均时间缩短31%且总体趋于稳定。

采用Fuzzy-PID 控制对比PID 控制结果，电机温度降低4.3%以及电耗减少16.1%，结果见表5。

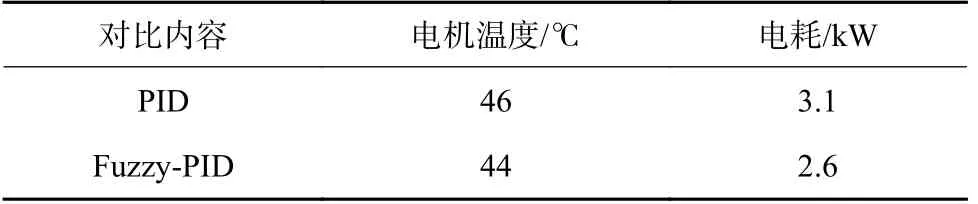
表5 结果对比Table 5 Comparison of results

5 结 论

1) 针对带式输送机功率大、长距离工作等特点，结合拉紧装置的时变性、非线性以及响应速度慢、调节能力差等缺点，设计了一种基于Fuzzy-PID 控制的液压拉紧系统。

2)在带式输送机启动响应阶段，Fuzzy-PID 控制器比PID 控制器响应速度提升了60%，超调量降低了67.5%。在张力突变调节阶段，当张力增加时，Fuzzy-PID 控制器的调节速度为0.3 s，超调量为2%，PID 控制器调节速度为0.7 s，超调量为6%。当张力减少时，Fuzzy-PID 控制器调节速度为0.3 s，超调量为2%，PID 控制器调节速度为0.6 s，超调量为4%。

3)仿真结果表明：采用Fuzzy-PID 控制的液压拉紧系统响应速度更快，超调量更小，并且对输送带的紧带和松带控制效果更加优异。

4)试验结果表明：采用Fuzzy-PID 控制的效果更佳优异稳定，且损耗更小，具有一定的应用价值。