基于双向耦合法的采煤机螺旋滚筒振动特性分析

张美晨 ，赵丽娟 ，李明昊 ，田 震

（1.常熟理工学院 机械工程学院, 江苏 苏州 215500；2.辽宁工程技术大学 机械工程学院, 辽宁 阜新 123000；3.辽宁省大型矿山装备重点实验室,辽宁 阜新 123000；4.沈阳理工大学 机械工程学院, 辽宁 沈阳 110168；5.周口师范学院 机械与电气工程学院, 河南 周口 466000）

0 引 言

采煤机螺旋滚筒高效截割、破落夹矸煤岩是一个复杂的演化过程，是多因素耦合作用的结果[1–3]，被截割煤岩的物理、力学性质的改变使其螺旋滚筒所受载荷具有非线性、时变性的特点，会导致螺旋滚筒产生振动与变形的程度随之发生变化，过于强烈的振动会降低采煤机的工作性能，因此分析多种不同截割工况下的螺旋滚筒振动特性对于提升采煤机工作可靠性具有重要意义，同时为采煤机智能开采中煤岩截割状态识别系统的构建奠定基础[4–5]。近年来众多学者针对采煤机螺旋滚筒振动特性展开大量深入的研究。辛红宝等[6]采用有限元分析法对不同齿座排列方式的端盘模态进行分析，最终获取混合排列方式的端盘可降低滚筒的振动；田震[7]等利用多软件协同仿真平台对采煤机模型进行振动特性仿真，对比分析了前后滚筒的振动强烈程度，结果显示前滚筒的振动明显大于后滚筒；杨琳琳等[8]采用非线性振动理论，分析截割转速的变化对滚筒振动的影响，得到合理的截割转速可减少滚筒的振动；王海舰等[9]利用试验测试方法提取了不同煤岩比工况下的滚筒振动信号，将其作为特征信息之一进行煤岩识别系统的搭建；陈洪月等[10]以试验测试得到的滚筒轴向截割载荷作为激励，分析了采煤机前后滚筒的振动量，得到了前滚筒的振动量高于后滚筒。上述研究成果为采煤机螺旋滚筒的设计提供了丰富的理论依据，但通过构建螺旋滚筒高效截割时与夹矸煤岩相互作用的双向耦合模型，开展其作用机理及动力传递规律的研究较少。

采煤机的截割过程可看作是由一系列离散介质组成的非连续整体在外界作用下发生移动的过程，而通过对离散介质的追踪能够有效获取外界作用下煤岩的变形及运动特征。双向耦合法由于可进行实时传递、交互、有效监测到离散介质行为信息而被广泛应用到不同生产领域，其中赵丽娟等[11]采用双向耦合法对摇臂壳体的疲劳寿命进行了分析；金鑫等[12]对采煤机螺旋滚筒的磨损特性展开了分析。以上研究对采煤机设计具有重要的指导意义，但其多是从数值模拟分析方面对采煤机性能展开讨论，且研究工况较为单一，对模拟分析和试验研究之间相互印证的研究较少。与此同时，对螺旋滚筒多种不同截割工况下工作过程中振动特性全面系统性的研究以及对产生的振动数据实施分析的同时，如何使其转换为可被智能化开采利用的有效信息也有待进一步深入探讨。

为此，基于项目组前期研究的基础，以MG2×55/250–BW 型薄煤层采煤机螺旋滚筒为研究对象，利用采煤机截割含夹矸煤岩的双向耦合作用机理，搭建其与多种不同截割工况下煤壁的双向耦合模拟试验平台，完成对物理样机的真实映射，通过仿真试验得到滚筒截割过程中受力及煤岩颗粒运行形态，提取不同煤岩工况下滚筒截割过程的振动信号，并采用STFT 算法将一维信号数据转化为二维时频谱图像，分析了煤壁中夹矸硬度以及层数的变化对螺旋滚筒振动特性的影响；通过采煤机截割煤岩试验平台对螺旋滚筒振动特性进行试验测试，对DEM–MFBD 双向耦合数值模拟方法的准确性进行了验证，为实现煤矿智能化开采过程中的煤岩截割状态识别系统构建提供有效数据支撑。

1 螺旋滚筒截割煤岩的双向耦合模型建立

1.1 煤岩离散元模型建立

1.1.1颗粒自定义接触模型

实际煤岩体表面呈现凹凸不平的特征，仅依靠离散元软件内部的传统Hertz-Mindlin 接触模型中定义的颗粒间摩擦力难以充分表征煤岩颗粒间的咬合作用，因此在其基础上，根据煤岩实际特征，添加煤岩体颗粒之间扭转力，通过构建自定义接触模型模拟其表面粗糙度。借助外部API 功能，创建新的源文件，将构建仿真模型过程中需要的头文件包含在源文件中，利用visual studio 外部编译环境对源文件进行编译，并将其定义为.dll 库文件，将库文件添加到EDEM 目录下的src 文件夹内，实现对插件的读取，完成自定义颗粒接触方式模型的构建[13]。煤层自定义接触模型中，接触单元由法向、切向及转动3部分组成，如图1 所示。煤岩颗粒接触参数，见表1。

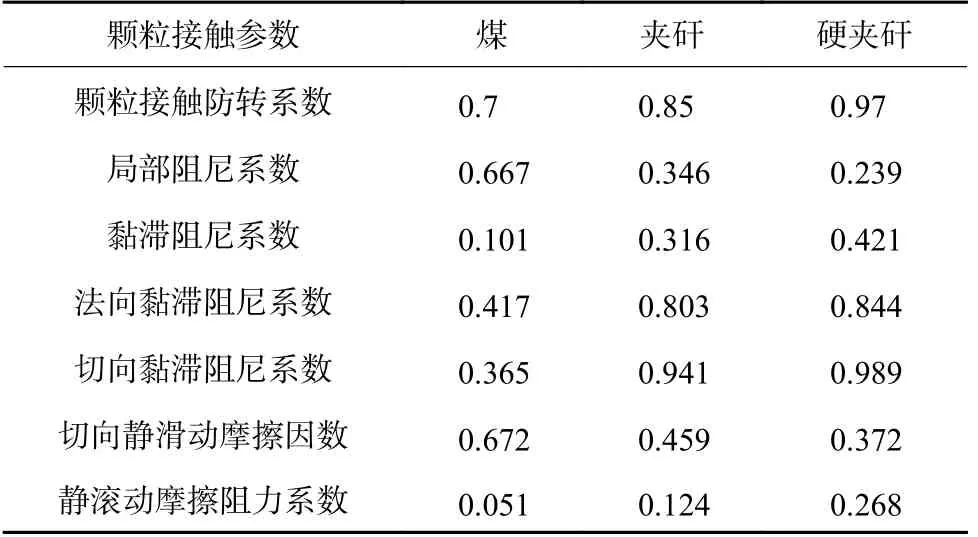
表1 煤岩颗粒接触参数Table 1 Contact parameters between coal-rock particles

图1 颗粒接触模型Fig.1 Particle contact model

1.1.2离散元模型建立

材料参数的选择对于离散元模型的求解具有重要影响，为了使所建模型更接近实际煤壁性质，需对煤岩颗粒材料进行测试。兖州矿区17 层煤平均厚度1 m，煤层倾角5°～13°，分布范围广，赋存稳定。但煤层结构复杂，煤层含夹矸1～2 层，厚度为0.02～0.44 m，岩性为炭质砂岩。按取样原理及检测标准对兖州矿区煤层进行取样测试，相关试验如图2 所示，表2 为试验所获取的煤岩具体物理力学性能参数。

表2 煤岩试样的基本物理、力学性质参数Table 2 Basic physical and mechanical property parameters of the coal and rock samples

图2 煤岩物理、力学性能测试试验Fig.2 Tests of the physical and mechanical parameters of coal-rock

分别构建全煤、含一层夹矸、含一层硬夹矸、含两层不同硬度夹矸的4 种工况下煤壁离散元模型。模型构建过程中煤岩颗粒的数目直接影响仿真效率，为了缩短计算时间，同时保证离散元模型能够实现对不同煤岩工况下螺旋滚筒截割煤岩的双向耦合过程进行仿真，煤壁模型尺寸设置为1 500 mm×1 500 mm×1 000 mm，并且虚拟煤壁模型对应滚筒的稳定截割状态，即煤壁表面已呈滚筒包络面形状，煤层、夹矸层具体厚度如图3 所示。

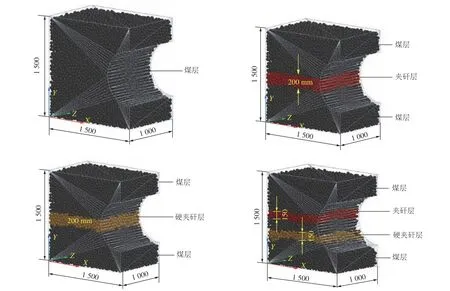
图3 煤壁离散元模型Fig.3 Discrete element model of coal wall

1.2 采煤机截割部刚柔耦合虚拟样机模型建立

利用Pro/E 软件建立采煤机截割部各零件刚性模型，再进行无干涉装配。以stp*格式将截割部装配体导入RecurDyn 中，定义各零件质量的同时根据截割部实际工作原理添加约束、驱动。采煤机截割部刚柔耦合虚拟样机模型建立过程比较重要的两个部分分别为：接触的计算与柔性零件的生成。

1.2.1接触的计算

接触的计算是模型不断进行自检的过程，通过检查几何位置是否处于接触状态去进行每一增量步的计算[14–15]。采用相对坐标系的接触分析算法[16]，其接触力模型如图4 所示，计算过程由式(1)确定：

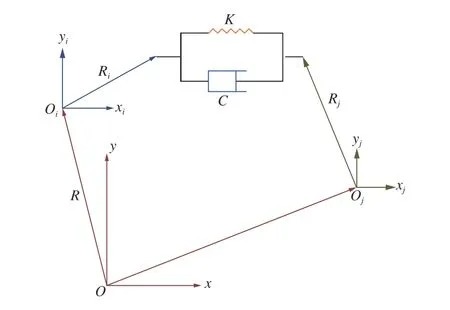
图4 接触力模型Fig.4 Contact force model

式中：δ为穿透深度，mm；K为接触刚度，N/mm；为接触点的相对速度，mm/s；C为接触阻尼，(N·s)/mm。

接触的添加需确定穿透深度、接触刚度以及接触阻尼。其中穿透深度通过有限元法进行求解，对采煤机截割部中相接触的零件体进行材料赋予、网格划分以及载荷的施加，求解后其后处理模块便可输出零件各节点的最大穿透深度。

接触刚度的计算则如式(2)—(5)[17–18]：

式中：Kt为接触总刚度，其由赫兹刚度Kh，弯曲刚度Kb，接触体变形刚度Kf组成；E为弹性模量；μ为泊松比；R为接触半径；B为齿宽；α为压力角；β1为齿顶渐开线与齿形中线夹角的余角；β2为齿形渐开线在基圆上所成弧夹角的一半；wf为初始啮合点曲率线和齿形中心线交点到齿根圆的距离；bf为齿根圆上的齿形宽；l、m、n和p为接触变形刚度相关系数。

接触阻尼[19–20]的选取可根据式(6)—式(7)确定。

式中：w为接触体有效接触面积；s为变形系数；γ为刚度比。

根据采煤机截割部零件的结构与材料，得到接触力计算模型中的接触刚度、阻尼、最大穿透量、非线性指数的取值见表3。

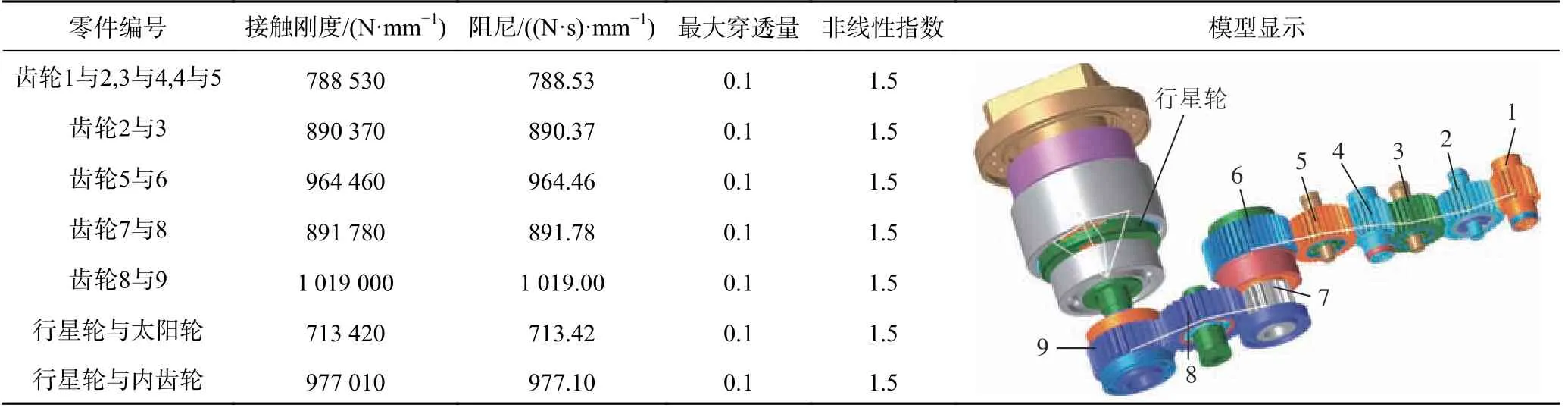
表3 采煤机截割部接触参数Table 3 Contact parameters of shearer cutting part

1.2.2柔性零件的生成

采煤机在实际工作过程中，由于煤层赋存条件复杂，螺旋滚筒将受到来自煤壁的高冲击、非线性载荷而出现应力集中和不同程度的变形。因此为了满足对这一过程的精准分析，将螺旋滚筒进行柔性化处理。最终将刚性滚筒替换成柔性件，形成截割部刚柔耦合虚拟样机模型如图5 所示。

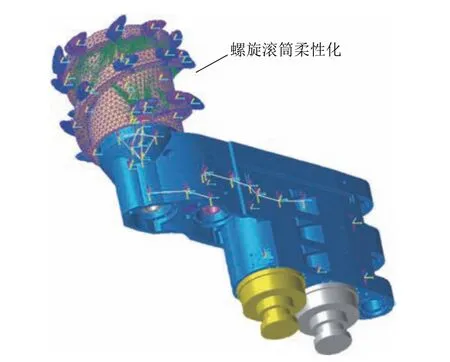
图5 采煤机截割部刚柔耦合虚拟样机模型Fig.5 Rigid-flexible coupling virtual prototype model of shearer cutting section

1.3 截割部DEM–MFBD 双向耦合模型建立

采煤机截割部截割过程的双向耦合模型通过EDEM–RecurDyn 之间的耦合接口建立可实现煤壁仿真模型与截割部刚柔耦合虚拟样机模型之间的关联，其采煤机截割部截割过程中EDEM–RecurDyn 双向耦合的交互过程如图6 所示。由图6 可知，Recur-Dyn 将采煤机截割部动力学模型的平移与旋转运动信息传递给EDEM 中对应的几何体，几何体的位置发生改变导致煤层工作面受力的位置、方向以及大小发生变化，EDEM 计算出此时煤壁对几何体的作用力并将数据回传至RecurDyn 中，在下一个时间步起始，RecurDyn 根据回传载荷信息与内部驱动信息计算出新的运动信息传递给EDEM，实现煤壁仿真模型与采煤机截割部相互作用过程中载荷与运动位移等数据的实时双向传递。采煤机截割部截割过程的双向耦合模型结构复杂，数据占比空间大，在EDEM 中仅导入螺旋滚筒，这可在不影响仿真精度的同时有效保证仿真速度，与此同时，螺旋滚筒作为采煤机工作机构安装至摇臂与煤岩直接接触，滚筒位置发生变化后，煤岩颗粒直接对滚筒产生作用力，这种作用力直接回传至RecurDyn 中，可完成对截割部动力信息的实时监控，提升仿真效率同时有利于对大量的煤岩截割状态实施仿真。

图6 截割部DEM–MFBD 双向耦合模型Fig.6 Bidirectional coupling model of DEM–MFBD in cutting section

2 仿真分析

2.1 螺旋滚筒截割过程分析

对采煤机截割部以转速为90 r/min，牵引速度为4 m/min 时的截割过程进行仿真，得到截割过程中煤岩颗粒的运动状态，以全煤工况为例，如图7 所示。由图7 可知，滚筒截割煤壁后，大部分颗粒在滚筒作用力下获得一个初速度从煤壁上脱落下来，靠近装煤区一侧由于自由表面的存在，抛出的煤岩颗粒所受轴向阻力较小，在空中受重力影响直接落入装煤区。远离装煤区一侧，抛出的煤岩颗粒在运动过程中若具有较大径向速度则向采空区做抛物线运动，若获得较小径向速度的颗粒则在轴向速度的共同作用下抛向装煤区。还有部分被截落的颗粒碰到截齿和煤壁后会落入叶片作用范围外，在叶片下方形成堆积，由于滚筒的连续转动，螺旋叶片使处于稳定堆积状态的煤岩颗粒间接触和作用力发生改变，堆积的颗粒打破稳定状态后再次沿滚筒轴线方向抛向装煤区。滚筒截割过程还会出现少量的煤岩颗粒不是正常剥落，而是被齿尖崩出使其向四周散落。

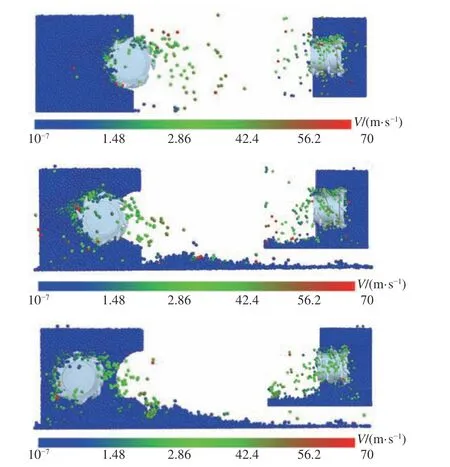
图7 截割过程中煤岩颗粒的运动状态Fig.7 Movement state of the coal and rock particles during cutting

分别对上述4 种工况的双向耦合仿真数据进行提取，得到截煤过程中螺旋滚筒的受力，与单向耦合进行对比，如图8 所示。由图8 可知，螺旋滚筒在与煤壁接触后，受力急剧增长，并出现明显的非线性变化。每种工况下双向耦合与单向耦合的变化存在差异。双向耦合过程全煤工况、含一层夹矸工况、含一层硬夹矸工况、含两层不同硬度夹矸工况下的螺旋滚筒载荷平均值分别为21 509.422 4、35 952.317 9、56 533.400 9、77 628.977 2 N，载荷波动系数分别为0.255 4、0.351 6、0.471 1、0.561 9；对应着4 种工况下，单向耦合过程中螺旋滚筒载荷平均值分别为19 791.178 7 、31 326.560 1、51 448.825 6 、71 388.187 4 N，载 荷 波 动 系 数 分 别 为0.207 2、0.297 5、0.411 9、0.483 4。由此可以看出随着煤壁中夹矸硬度与层数的增加，螺旋滚筒载荷平均值、载荷波动系数均增加。基于双向耦合法的仿真结果其螺旋滚筒载荷平均值与载荷波动系数均比单向耦合仿真结果有所提升，4种工况下螺旋滚筒载荷平均值分别提升了8.68%、14.76%、9.89%、8.74%，载荷波动系数分别提升了23.26%、20.13%、14.37%、16.24%。

图8 不同煤岩工况下滚筒受载的单双向耦合对比Fig.8 Comparison of single and bidirectional coupling of drum load under different coal-rock working conditions

2.2 螺旋滚筒振动加速度频率响应分析

采煤机螺旋滚筒所受载荷具有非线性、时变性和强耦合性等特点，在截割过程中会产生强烈的振动和较大的变形，为了提高采煤机工作过程中的可靠性，根据双向耦合法的仿真结果分析螺旋滚筒在不同煤岩工况下的振动特性，提取4 种工况下螺旋滚筒的三向振动加速度曲线，如图9 所示。统计得到滚筒质心三向加速度数值见表4。螺旋滚筒在截割过程中，X、Y、Z方向均出现不同程度的振动，其中Y方向(截割阻力方向)振动加速度最大，Z方向(牵引阻力方向)振动加速度次之，X方向(侧向力方向)振动加速度最小。截割全煤工况过程中螺旋滚筒截割阻力方向的振动加速度在–15 781.121～22 258.997 mm/s2范围内波动，有效值为2 642.139 mm/s2；截割含一层夹矸、含一层硬夹矸、含两层夹矸工况过程中，截割阻力方向的振动加速度分别在–20 908.425～26 134.872、–30 727.719～35 583.154、–35 853.527～42 751.179 mm/s2范围内波动，有效值分别为3 811.396 、5 632.322、7 045.288 mm/s2。由此可知，随着试件模型中夹矸硬度以及层数比例的增加，截割过程中螺旋滚筒的振动不断增大，最大振动加速度有效值的差值为4 403.149 mm/s2，并且其振动变化趋势与载荷变化具有一定的相似性，说明滚筒截齿、端盘、叶片、筒毂受载是影响螺旋滚筒振动的一个因素。

表4 滚筒质心三向加速度数值Table 4 Three direction acceleration value of spiral drum centroid

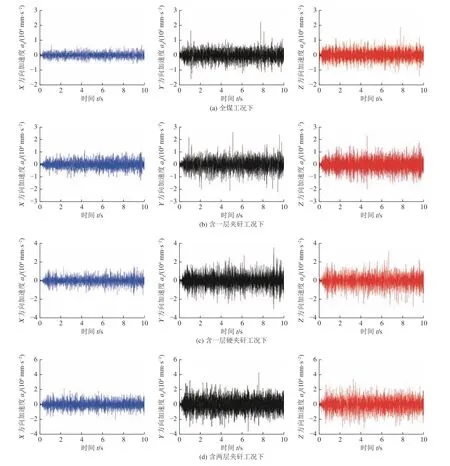
图9 不同煤岩工况下螺旋滚筒三向振动加速度曲线Fig.9 Three direction vibration acceleration curve of spiral drum under different the coal and rock conditions

通过上述图9 与表4 对采煤机截割部截割过程中螺旋滚筒所受振动信号的时域信息分析可知，当含夹矸层数相同时，煤岩坚固性系数较大的工况其振动加速度波动的幅度较大，当含夹矸层数不相同时，夹矸层数越多其振动加速度波动变化幅度越大，但不同种煤岩工况下其振动加速度的波形相似，差异信息少，并且其波动范围呈现无规则变化，仅依靠螺旋滚筒振动信号的一维时域特征会造成频域信息的丢失，难以反映煤岩截割状态与其相对应振动信息之间的非线性关系，无法对智能化无人开采中煤岩详细截割状态的准确辨别提供准确的振动特征信息。因此选择可将判别煤岩截割状态信息的振动信号从时域转换为时频域的短时傅里叶变换(STFT)方法，将螺旋滚筒在截割阻力方向的振动加速度一维曲线转化为二维时频谱图像，防止振动特征信息丢失，为后续的智能化无人开采奠定基础[21]。

STFT 将煤岩截割过程中产生的非平稳振动信号进行分割，使其变换为多个近似的平稳信号，多个近似平稳的信号经短时傅里叶变换后通过窗覆盖的方式将其进行整合，实现煤岩截割振动信号从时域特征到时频域特征的映射。STFT 变换以傅里叶作为基本算法，有效避免了变换后的时频谱图像出现交叉项等问题，更易于说明图像本身所表示的物理意义。通过STFT 方法在对反映煤岩截割状态的振动信号进行转换的过程中，需重点考虑窗函数类型[22]、窗函数的长度Lt[23]和窗的重叠量Ln[24]。

1）窗函数类型的选取。STFT 变换中包含多种不同的窗函数，其中凯塞窗可通过对β参数的选择实现主瓣宽和旁瓣衰减之间的平衡，数学模型为

式中：Lt为窗的长度；–(Lt–1)/2≤n≤(Lt–1)/2，i为修正的阶数。当参数β的数值越大，主瓣越宽，旁瓣衰减速度越大；当参数β的数值越小，主瓣越窄，但其旁瓣衰减速度则减小。

煤岩截割过程中，振动信号的波形并非呈完全稳定状态，当振动信号呈非稳定状态时，需降低w(n)窗的长度，主瓣则随之变宽，那么此时为了保持频域分辨率，减少频域的特征的丢失，需降低β值，而凯塞窗的旁瓣衰减速度就要随之下降，完成匹配；当振动信号呈较稳定状态时，可选取较大的w(n)窗长度，主瓣变窄，此时提高β值既可保留频域特征能量，又可获得较好的通道抗干扰能力。因此，采用凯塞窗平衡煤岩截割状态信号处理中频域特征信息保留与抗干扰性之间的权重。

2）窗长度Lt的确定。振动信号转换过程中频域特征信息的保留效果除受窗函数类型的影响之外，窗的长度也对其产生影响，当窗的长度值越大则主瓣越窄，反之会使主瓣的宽度Lb增加，降低频域特征效果，其可表示为

式中：N为主瓣的离散频率大小；fs为信号的采样频率，Hz；Lb≤Δf，因此窗长度Lt的取值需满足

式中：Δf=fn+1–fn，fn+1和fn为相连的两个谐频率。

3）窗的重叠量Ln。在STFT 频谱合成过程中，窗重叠量根据恒定重叠约束法构建的数学模型为

式中：Ha(n)为最终的包络；w(n)为窗；a为帧索引；S为步长；Lm为重叠量的振动幅度偏移量。

综合上述式(13)—式(17) 分析，对不同工况下的煤岩截割过程中螺旋滚筒的振动信号进行STFT转换，其参数设置见表5。经过STFT 分解合并后，得到不同截割状态下大小为128×128 的螺旋滚筒振动信号二维时频谱图像如图10 所示。

表5 STFT 变换的参数设置Table 5 Parameter setting of STFT transform

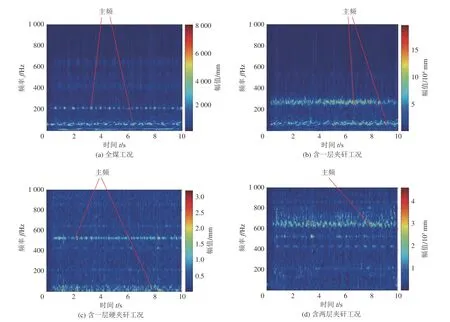
图10 螺旋滚筒振动信号二维时频谱图像Fig.10 Time-spectrum image of vibration information of spiral drum

图10 中，煤的坚固性系数为1.4 的全煤工况(图10a)其主频处的能量特征集中分布在60、210 Hz处；煤的坚固性系数为1.4、夹矸的坚固性系数为3.5 的含一层夹矸工况(图10b)其主频处的能量特征集中分布在50、270 Hz 处；煤的坚固性系数为1.4、硬夹矸的坚固性系数为5.1 的含一层硬夹矸的工况(图10c) 其主频处的能量特征集中分布在20、520 Hz 处；煤的坚固性系数为1.4、夹矸的坚固性系数为3.5、硬夹矸的坚固性系数为5.1 的含两层夹矸工况(图10d)其主频处的能量特征集中分布在620 Hz 处。由此可知，随着煤和岩的坚固性系数的改变，4 种工况下振动信息在周期、振幅等特性方面具有明显不同，STFT 将此种差异凸显后集中显示在时频谱的主频处。产生此种差异主要是由于随着煤壁含有夹矸类型以及数量的不同，螺旋滚筒在截割时煤壁硬度发生了改变，螺旋滚筒所受瞬时载荷发生突变，因此滚筒存在明显振动的幅值发生变化，截割稳定性降低，采煤机的工作可靠性降低。

2.3 螺旋滚筒模态振型分析

为了进一步全面分析螺旋滚筒的振动特性，通过模态分析模块结合螺旋滚筒模型属性，计算得到其各阶模态频率及相应振型特征，见表6。由表6 可知，截割全煤工况过程中，螺旋滚筒1～10 阶固有频率变化范围为10.41 ～70.16 Hz，最大变形量为9.7 mm，最小变形量为3.1 mm；截割含一层夹矸、含一层硬夹矸、含两层夹矸工况过程中，螺旋滚筒1～10 阶固有频率变化范围分别为12.46～73.94，13.87～75.78，14.14～77.71 Hz，最大变形量分别为10.1、11.2、11.7 mm，最小变形量分别为4.1、4.6、4.9 mm。4 种不同工况下，螺旋滚筒各阶模态振型存在相似规律，分别提取4 种煤岩工况的第8 阶模态振型，如图11 所示。第8 阶模态振型特征主要显现为整个螺旋滚筒组合变形，变形的位置主要集中在截齿部位，截齿与叶片、端盘焊合处出现明显变形量，齿尖部分变形最大、振动最为强烈，叶片与筒毂焊合处的变形量相对较小、振动较为平稳。随着煤壁中含有夹矸硬度的增加，各部位的变形量均发生变化，其中截齿部位变化最为强烈。煤壁硬度的变化引发的螺旋滚筒振动变形会导致截齿磨损，严重甚至脱落，影响螺旋滚筒的生产效率；叶片发生的变形会使其装煤作用减弱，严重会加剧磨损直接致使螺旋滚筒的装煤率大大降低，影响采煤机的工作性能。

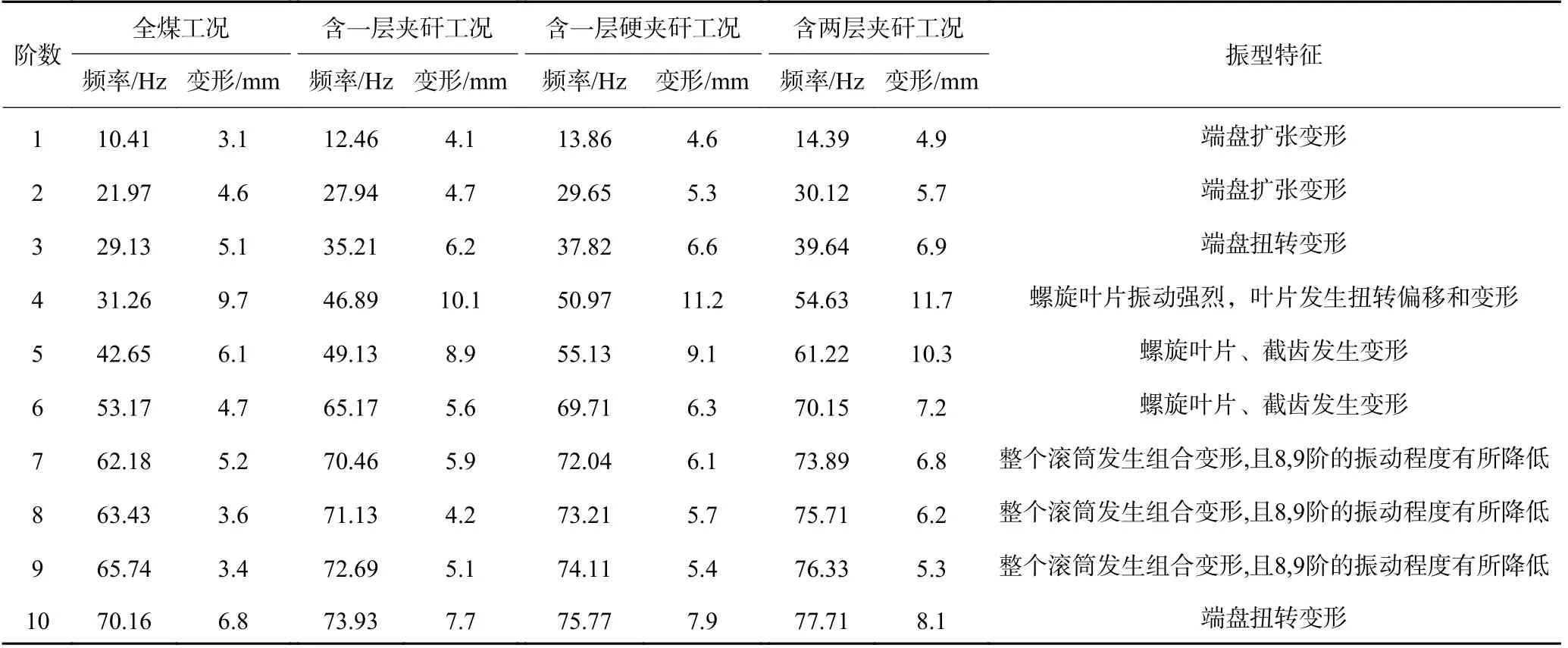
表6 各阶模态频率及相应振型特征Table 6 Modal frequency of each order and corresponding vibration mode characteristics

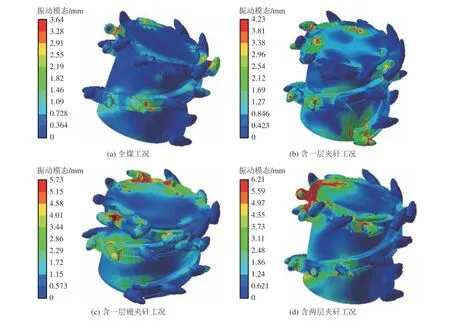
图11 不同煤岩工况下螺旋滚筒第8 阶振动模态Fig.11 8th order vibration mode of spiral drum under different the coal and rock conditions

3 基于相似理论的采煤机振动信号测试试验

为测试上述研究方法、研究结果的正确性，在大型工矿装备重点实验室对采煤机螺旋滚筒的截割过程开展试验测试。基于实验室原有的采掘设备改造现有采煤机截割煤岩试验平台。

3.1 基于相似理论的拟实煤岩壁、滚筒构建方法

3.1.1量纲分析

为使采煤机截割煤岩试验平台能够准确模拟采煤机原型的实际截割过程、与仿真试验参数相匹配，需保证相似采煤机模型与原型结构几何相似、运动学参数相似、截割性能参数相似，煤壁与天然煤岩的物理力学性质相似。因此在相似准则推导中，需同时考虑到采煤机结构参数及运动学参数、煤壁物理力学性质参数。基于此，选取滚筒直径、滚筒转速、牵引速度、力、力矩、截割功率、振动加速度、密度、强度作为相似参数。运用MLT(质量系统)量纲分析法，根据夹矸煤岩各项参数，建立夹矸煤岩的各项参数量纲，见表7。

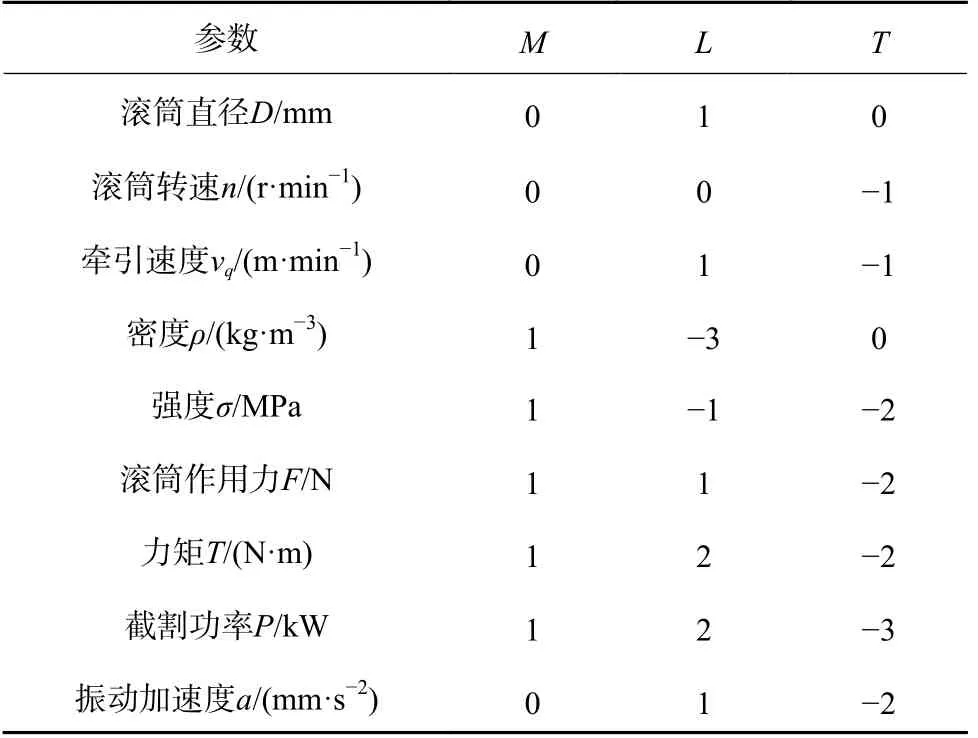
表7 参数量纲Table 7 Parameter dimension

依据相似第2 定理，π 法则(相似准则)的数目等于相似系统中所有物理量个数之和减去基本量纲的参数个数，因此相似准则数目为6 个。根据质量量纲系统，以质量M、长度L和时间T为基本量进行研究，夹矸煤岩各项参数的指数设置为a1，a2，a3，···，a9，列出量纲矩阵见表8。

表8 量纲矩阵指数Table 8 Dimensional matrix index

根据表8 中各个量纲指数值，由量纲关系可得到其次线性方程，如式(13)—式(15)所示：

建立夹矸煤岩各项参数的π 矩阵，见表9。

表9 夹矸煤岩各项参数的π 矩阵Table 9 π matrix of various parameters of gangue coal and rock

3.1.2相似系数确定

相似模型设计中，以长度L为基准量，设几何相似比CL=K1=0.5；考虑截割速度vi为截齿齿尖线速度，其式为

截割速度vj=3～4 m/min，抗压强度σ≈10f，因此确定相似系数见表10。

表10 相似系数Table 10 Similarity coefficient

根据相似原理设计的滚筒三维实体模型以及加工出来的实际模型如图12 所示。按相似比计算出相似含夹矸煤壁(试验用煤壁)对应的原型数值结果，见表11。将相似模型和原型数值结果进行对比，依据相似理论，得到黏结参数相似反推结果，原型黏结参数和相似模型反推之后的结果误差在允许范围内[25–27]，均小于3.5%，验证了黏结参数相似准则推导的正确性，即依据相似理论制作煤壁的方法可行，其具体制作的过程如图13 所示。

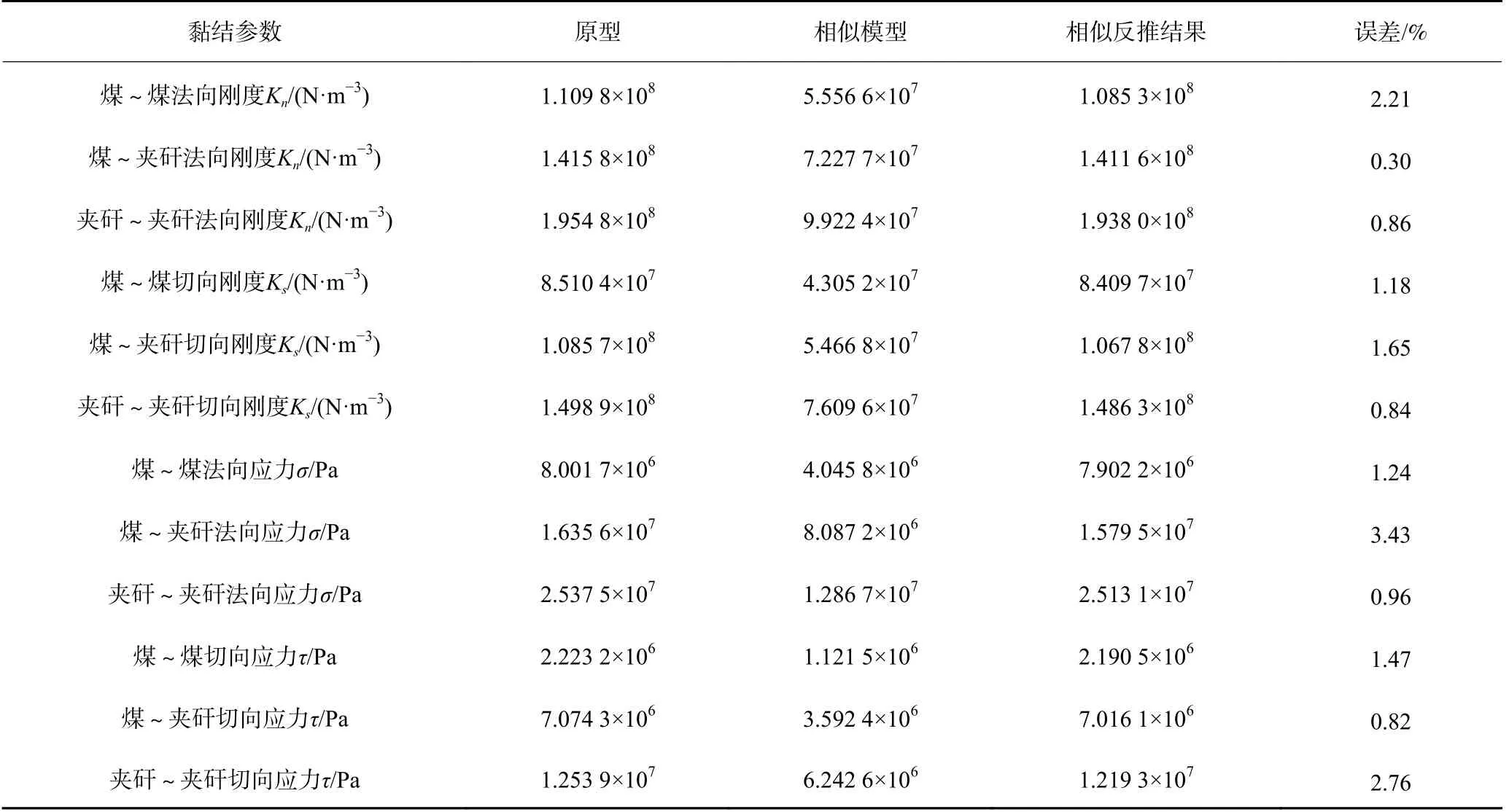
表11 原型和相似模型黏结参数对比验证Table 11 Comparison and verification of prototype and artificial coal wall model parameters

图12 滚筒模型Fig.12 Drum model

图13 煤壁制作过程Fig.13 Coal wall production process

3.2 采煤机截割煤岩试验平台搭建

煤岩截割综合试验系统主要包括机械、液压、试验台操控、监控系统及传感器、数据传输以及上位机部分，其中试验台机液系统主要由试件夹持装置、截割装置以及泵站等辅助元器件组成，搭建过程如图14 所示。

图14 试验系统Fig.14 Experimental system

3.3 试验方案设计

试验通过对煤壁的分层分段处理设定4 种与仿真工况一致的煤岩截割状态，见表12，通过调整螺旋滚筒的位置对不同煤岩工况实施截割试验。为了保持试验系统与虚拟仿真系统的高度一致性，将DH311E 型三向压电式振动加速度传感器安装在采煤机螺旋滚筒后端，通过信号数据采集处理系统采集其在截割过程中的振动信号，其本次试验的现场测试工作状态如图15 所示。

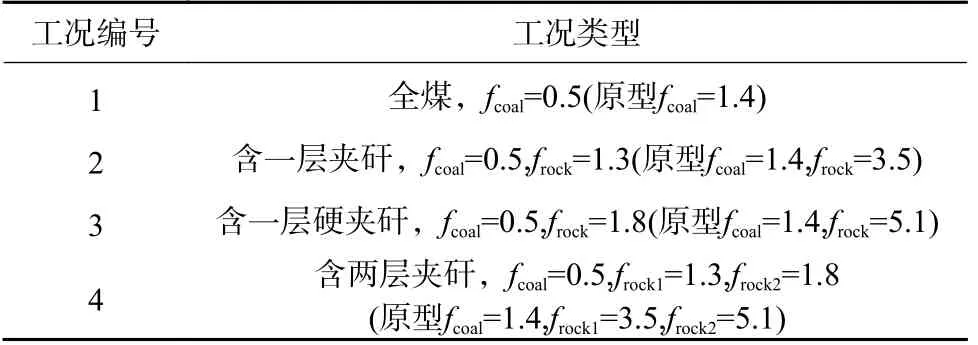
表12 试验工况Table 12 Experimental conditions

图15 现场测试Fig.15 On site testing

3.4 结果分析

试验前通过采煤机的往复空载运行对其采煤机、工作台的运转、导轨、信号的测试与接收等设备实施检测，确认各系统无误后进入截割试验。试验中，采煤机的牵引速度为2.417 m/min，螺旋滚筒的转速为113.57 r/min。试验结束后，其煤壁状态如图16 所示，通过DH5922D 型信号测试分析仪获取DH311E 型三向压电式振动加速度传感器采集到的螺旋滚筒三向振动信号，根据相似比将信号转化处理后绘制为一维时域图，得到相似反推结果曲线如图17 所示。由图17 可知，测试螺旋滚筒在截割过程中振动信号呈现明显的非线性变化，其呈现的振动强烈表现为截割阻力方向最大、牵引阻力方向次之、侧向力方向最小，DEM–MFBD 数值模拟方法获取的振动加速度三向之间的仿真结果与此试验实测反推结果相吻合。

图16 截割后煤壁状态Fig.16 Coal wall state after cutting

图17 螺旋滚筒三向振动信号试验反推曲线Fig.17 Experimental inversion curve of three direction vibration signal of spiral drum

为了进一步验证DEM–MFBD 数值模拟方法的准确性，计算统计4 种不同煤岩截割工况下的螺旋滚筒振动信号，得到测试滚筒三向振动加速度有效值见表13。

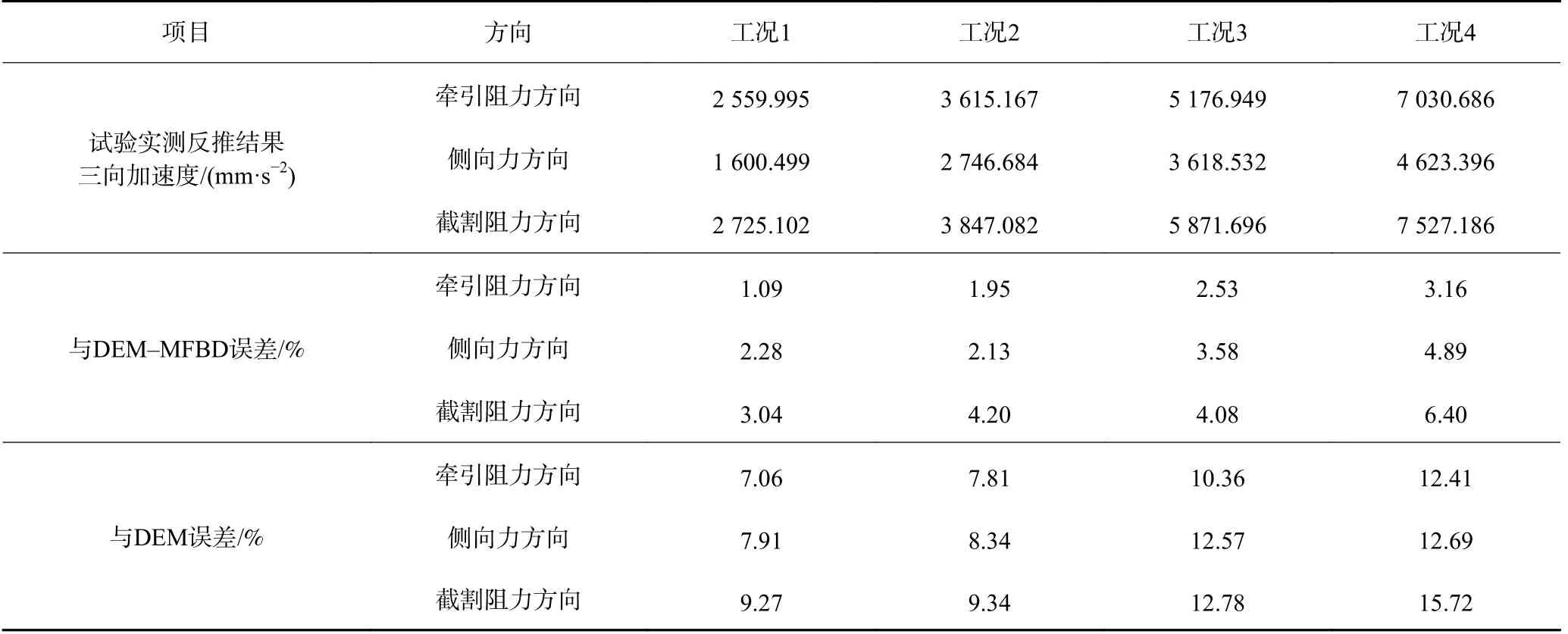
表13 试验与仿真结果对比Table 13 Comparison of experimental and simulation results

由表13 可知，截割含不同夹矸煤壁时的滚筒振动响应与DEM–MFBD 数值模拟仿真结果之间存在的误差较小，DEM–MFBD 数值模拟仿真结果与测试反推结果变化规律一致。4 种工况下牵引阻力、侧向力和截割阻力方向加速度误差随着煤岩硬度的增大而出现增加的趋势，其中三向振动加速度最大误差分别为3.16%、4.89%和6.40%。由于仿真煤壁是颗粒黏结形成的均匀煤岩，试验煤壁是由石膏、水泥等原料搅拌制作，因此结果存在不同程度的误差。与此同时，试验装置结构与实际采煤机截割部结构存在差异性，这也是造成不同程度误差的原因。然而，虽然采煤机截割部结构不同，导致振动模态不同，固有频率不同，产生的振动信号不同。但基于虚拟样机的仿真及试验研究均与实际工况一致，无论什么样的结构参数对研究的结果影响不大。DEM 数值模拟仿真结果与测试反推结果相差较大，其中三向振动加速度最大误差分别为12.41%,12.69%和15.72%，与DEM–MFBD 数值模拟仿真结果误差分别相差73.73%、59.49%、69.81%。4 种工况下三向振动加速度DEM–MFBD 数值模拟的仿真结果与试验实测反推结果之间的误差均小于DEM 离散元数值模拟的仿真结果，因此采用基于双向耦合作用机理的数值模拟方法提取的振动信号更加符合螺旋滚筒实际工作状态。

4 结 论

1)利用DEM–MFBD 数值模拟搭建采煤机截割部与煤壁的双向耦合平台，对采煤机螺旋滚筒的截割过程进行模拟试验，试验结果表明DEM–MFBD仿真下螺旋滚筒载荷平均值与载荷波动系数均比DEM 仿真结果有所提升。

2)截割过程中不同煤岩工况条件下螺旋滚筒所受到的截割阻力和牵引阻力方向的振动明显高于侧向力方向；随着煤壁中夹矸硬度以及层数比例的增加，螺旋滚筒三向的振动信号以及最大振动信号幅值均不断增大，并且其振动变化趋势与载荷变化具有一定的相似性。利用短时傅里叶变换将其转化为二维时频谱图像，结果表明：不同工况下时频谱图像的特征样本效果优于各工况的时域一维信号曲线，主频能量位置、范围大小、特征团形状等信息具有明显区别。通过不同煤岩工况条件下的螺旋滚筒模态分析得到螺旋滚筒的变形量随煤壁中含夹矸种类的不同发生变化，其中截齿部位变化最为强烈。

3)试验结果表明：4 种不同煤岩工况下，DEM–MFBD 数值模拟结果与试验实测反推滚筒截割阻力方向振动信号最大误差分别为3.04%、4.20%、4.08%、6.40%；DEM 数值模拟结果误差分别为9.27% 、9.34% 、12.78% 、15.72% 。DEM–MFBD 数值模拟方法更能准确获取螺旋滚筒截割过程中的振动特征，为煤岩截割状态识别系统数据信号的获取提供了一种新的方法。同时利用DEM–MFBD 双向耦合作用机理能够有效地反映出采煤机实际工作状态，为螺旋滚筒的强度以及可靠性分析提供了新平台。