炭质泥页岩剪切破坏声发射特性及其分形特征
代鑫, 胡斌*, 李京, 曹建军, 崔喜兴
(1.武汉科技大学资源与环境工程学院, 武汉 430081; 2.冶金矿产资源高效利用与造块湖北省重点实验室, 武汉 430081)
含炭质泥页岩软弱夹层广泛分布于中国中南、西南地区的矿山边坡中,易受自然环境变化或人为扰动影响而失稳,对边坡工程和隧道围岩等工程的稳定性存在严重威胁,但岩石的失稳破坏过程可通过声发射技术进行监测和预报,声发射参数中蕴含着岩石破坏过程信息,同时声发射分形理论可以通过分形维数的变化来反映岩石破坏过程中微裂纹的演化规律和破坏前兆特征[1]。因此,可通过炭质泥页岩破坏的声发射参数及其分形特征来探究含炭质泥页岩软弱夹层的破坏机理和失稳前兆特征。
近些年来,许多学者将声发射技术和分形理论应用到岩石破裂机制的研究中,王创业等[2]探究了岩石和类岩石材料在单轴压缩破坏过程中的声发射特性及其差异。胡英等[3]运用时频分析方法,提出一种新的特征参数,基于此得到岩石破裂前兆信息。高安森等[4]通过红砂岩单轴压缩声发射试验,探究了红砂岩在临界加速失稳阶段的破坏特征和失稳前兆。刘文德等[5]通过对灰岩开展单轴压缩试验,证明了灰岩破裂所产生的声发射事件数的时间序列存在分形特征。龚囱等[6]对红砂岩进行了蠕变声发射实验,运用分形理论,得出声发射震源值演化规律。孙博等[7]进行不同层理倾角的板岩单轴压缩试验,分析了声发射计数的多重分形特征,得出板岩的破坏前兆和预警时间。龚囱等[8]研究了钢筋混凝土受剪梁声发射参数在不同剪跨比和粗骨粒径的条件下的发展规律。王伟等[9]通过对砂岩进行常规三轴和三轴循环加载声发射试验,分析了砂岩声发射特性和声发射计数分形特征,得到了岩石裂痕发育的演化规律。杨东杰等[10]设计了岩石预损试验,阐述了预损后花岗岩的振铃计数分形演化。以上研究表明岩石、类岩石等材料的声发射参数都具有分形特征且蕴含着失稳破坏过程信息,但大多数学者只采用一种声发射参数进行分形特征的研究,所得出的失稳前兆信息单一且难以得出不同参数中所蕴含失稳前兆信息之间的差别,同时软弱夹层(炭质泥页岩)作为矿山边坡中极易造成滑坡事故的危险源,却少有学者对其进行基于声发射的失稳前兆研究。
考虑到上述现有研究的不足,对少有学者关注的软弱夹层(炭质泥页岩)进行剪切破坏声发射试验,考虑了不同声发射参数之间的联系与差别,选取多个参数进行分形特征研究,综合确定炭质泥页岩失稳前兆信息,以避免研究结果的依据单一,同时,对比分析,探索更适合作为炭质泥页岩破坏前兆信息的参数,旨在为岩石失稳破坏全程裂隙演化和失稳预测提供理论依据。
1 声发射试验
1.1 岩样制备
试验所用炭质泥页岩取自四川省峨眉山地区二叠系坚硬石灰岩层中的软弱夹层,夹层厚约为0.1~0.8 m,产状与上下岩层一致。将所取岩样切割为尺寸为150 mm(长)×75 mm(宽)×75 mm(高)的长方体试件(图1),加工过程中尽量保证试样不受扰动。

图1 炭质泥页岩岩样Fig.1 Carbonaceous shale
1.2 试验设备及方法
岩石剪切试验在团队自主研发的微机伺服控制岩石剪切-渗流耦合试验机上进行,设备如图2所示。主要适用于岩石剪切试验、剪切渗流和剪切蠕变试验。该设备采用高刚度整体框架主机、全数字测控器,具有多个测控通道可对任意一个通道进行闭环控制。

图2 WAJS-100型微机伺服控制岩石剪切-渗流耦合试验机Fig.2 WAJS-100 microcomputer servo control shear-seepage coupling testing machine for rock
此次试验采用美国物理声学公司生产的PCI-2型声发射测试分析系统(图3),选择的传感器为RS-2A型,前置放大器可以将信号放大100倍。试验时将4个探头两两一组,贴于岩样两个相对的侧面,并使4个探头不在同一平面,采样速率设为3 MHz,门槛电压值为100 mV。

图3 声发射测试分析系统、传感器、前置放大器Fig.3 Acoustic emission system of analysis, sensors and preamplifiers
对炭质泥页岩进行剪切破坏试验。法向加载采用力控制,切向加载选择位移加载,加载速率设置0.2 mm/min。先施加法向力,稳定30 s后,再施加剪切力。试验过程中采集时间、剪切位移、声发射振铃计数、能量、振幅等试验数据。
2 声发射试验结果分析
一般地,当岩石在剪切荷载下发生破坏,引起岩石内部部分能量以应力波的形式扩散,即形成声发射信号[11]。选择振铃计数、能量、振幅、上升时间与幅度的比值RA、振铃计数与持续时间的比值AF对试验结果进行分析。图4~图6为剪切力、时间和不同声发射参数之间的关系曲线。

图4 剪切力-时间-振铃计数曲线Fig.4 Stress-time-counts curve

图5 剪切力-时间-能量曲线Fig.5 Stress-time-energy curve

图6 剪切力-时间-振幅曲线Fig.6 Stress-time-amplitude curve
从图4~图6可以看出,在实验刚开始时岩石内就发生了声发射活动,这是因为此时岩石处于压密阶段(0~150 s),随着原有裂隙被压实,岩石颗粒间发生错动,同时也伴有少量微裂纹的生成,声发射特性表现为小事件较多,能量值和振幅值波动较大,新产生的微破裂强度大小不一。随试验的进行,声发射信号值都逐渐下降,声发射能量和振幅逐渐稀疏,这是因为岩石进入弹性变形阶段(150 ~400 s),原有裂隙已被压实,岩石发生弹性变形,体积减小,声发射特性表现为能量逐渐降低,振幅相对减小。在岩石进入塑性变形阶段(400~500 s),新裂纹不断产生、汇集、贯通,声发射特性表现为声发射振铃计数和能量值在总体趋势上逐渐上升,在临近破坏时达到峰值。
图7为炭质泥页岩临近破坏时裂纹的声发射三维定位演化图,可以看出,红色球体及其在x、y、z面上投影数量上越来越多,形状也越来越大,说明在此时岩石内部已产生大量裂纹并向四周扩展,印证了此时声发射振铃计数和能量值极具骤增的变化。值得注意的是,此阶段岩石出现约30 s的声发射平静期(450~480 s),平静期内振铃计数、能量值均有明显的大幅减弱,平静期结束后声发射活动又瞬间激增,紧接着岩石发生破坏,平静期这一特殊现象可作为岩石破坏前兆信息。

图7 炭质泥页岩临近破坏时裂纹的声发射三维定位演化图Fig.7 Three-dimensional localization evolution of cracks in carbonaceous shale near destruction
声发射RA、AF作为岩石破裂机制的依据,常用来区分岩石破坏类型,判定方法如图8所示,高RA低AF为声发射剪切波特征,对应岩石剪破坏,高AF值低RA则对应张拉破坏[12]。RA为上升时间与幅度的比值,AF为振铃计数与持续时间的比值,岩石RA-AF分布如图9所示,其中高AF低RA的分布明显少于高RA低AF,故而炭质泥页岩样的破坏类型是为以剪切破坏为主的张剪复合型破坏。
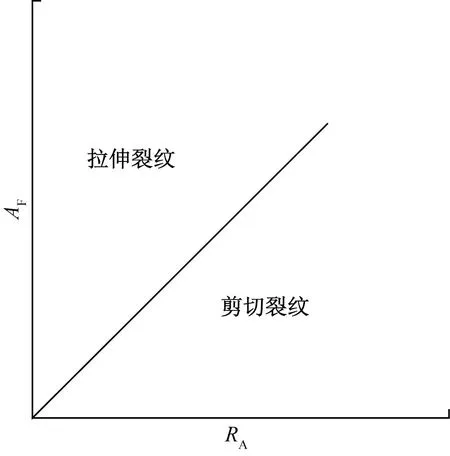
图8 破坏类型判定方法Fig.8 Criteria for fracture classification

图9 RA-AF分布图Fig.9 RA-AF distribution
3 声发射信号分形特征研究
3.1 分形理论和关联维数计算模型
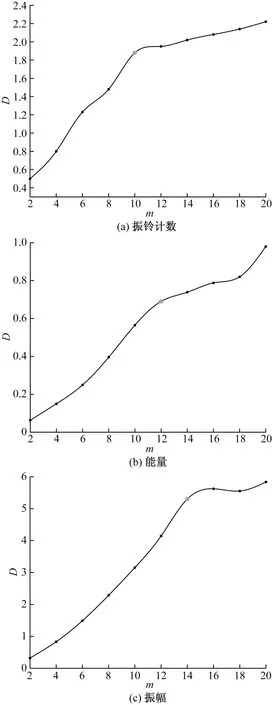
一般地,常用的声发射表征参数都可以构成单独的声发射时间序列[13],分形维数是分形理论的基本量,它可以定量描述分形[14],其中关联维数是最常用的分形维数之一。G-P算法可将声发射基本参数时间序列作为研究对象,每个声发射基本参数时间序列对应容量为n的序列集Xn={x1,x2,…,xn},然后在该时间序列的基础上构造m维的相空间(m (1) 对于给定尺度r,可表示为 r=kr0 (2) 式(2)中:r0可表示为 (3) 对每一个给定的尺度,都可得到一个C(r)。在双对数坐标系中可得到一系列点:[lnCr(k)],lnr(k)],对这些点进行数据拟合,拟合直线的斜率就是声发射参数序列的关联维数D,即 (4) 选择振铃计数、能量、振幅3个参数进行关联维数的计算和分析。首先编写该算法的程序,然后将声发射参数、时间序列、应变等导入程序,实现对声发射参数的归一化处理、相空间重构和关联维数的计算。 G-P算法重构了岩石损伤破坏过程动力系统吸引子的多维空问,但对于系统空间的吸引子的性质,相空间维数m的取值至关重要[16]。在对m取值时,不可将m盲目缩小,这样会导致重构的相空间处于低维状态,使得两个原本不接近的相点产生相邻的假象。也不可将m过度放大,这样会使得原本接近的相点造成相离的假象,导致相空间吸引子分散。所以,应选取合适的m进行计算。 m取值一般采用几何不变量法[17],在MATLAB环境下将m依次取2、4、6、8、10、12、14、16、18、20,在600个观测尺度r下分别分析3个声发射参数的r-C(r)双对数关系。 如图10所示,对于振铃计数、能量、振幅三个声发射参数在同一m下,当r很小时,每两个散点的距离都比较大,即每两个点的C(r)相差很大,相点距离都比较远,所以对于r的小幅增大,C(r)并没有呈现连续的增大,而是跳跃式增加,即不存在分形现象。当r取值很大时,C(r)趋近于1,lnC(r)趋近于0,散点构成曲线虽然连续但是已成为一条直线,随r的增大,关联维数一直为0,不存在分形现象。而当lnr取值为2~4时,振铃计数、能量、振幅3个声发射参数在10个m下的观测尺度r和关联函数C(r)的对数曲线会部分接近一次线性关系,即此时声发射参数是具有分形特征的,而r-C(r)双对数散点曲线线性回归的斜率就是关联维数。 图10 不同声发射参数在不同m值下r-C(r)双对数散点图Fig.10 r-C(r) double logarithmic scatter plot for different m values and parameters 如图11所示,3个参数的关联维数D随m的增大先呈线性增加,在m增大到某一点后,曲线斜率逐渐下降且D增长速度逐渐稳定。一般取D收敛的第一点作为合适的相空间维数m,即在计算3种声发射参数的关联维数时m分别取10、12、14。 图11 不同声发射参数在不同m值下的关联维数DFig.11 The correlation dimension D of different acoustic emission parameters at different values of m 通过声发射参数计算出来的关联维数可以描述岩石声发射分形演化行为[18]。基于3.2节对分形特征的判定和确定的m,在MATLAB环境下,每隔2%的应变比对声发射参数进行一次关联维数D的计算,直至应变比达到100%。 图12为在不同应变比下的分形维数和对应计算位置剪应力的曲线,可以看出,在加载初期,振铃计数、能量、振幅的关联维数不断升高,进入升维状态,此时岩石内部的原生裂隙被压实闭合,而后又随压力的增加,这种被压密的有序性逐步提升,故而关联维数逐渐上升。随试验进行,能量的关联维数率先发生变化,由上升趋势转为上下波动,表明能量的关联维数进入了动态波动阶段,而后振铃计数与振幅的关联维数才相继进入动态波动阶段,在此阶段岩石内部不断出现微破裂的发育和闭合,但微破裂的发育和闭合随时间不均匀出现,处于一种“混沌”状态,所以关联维数呈现出无规则的上下波动。随压力进一步升高,能量的关联维数最先进入降维阶段且降维幅度较大,持续时间较长,而振铃计数和振幅的关联维数分别在塑性变形阶段中期和后期才进入降维阶段且降维幅度较小,持续时间较短。关联维数的降维现象意味着此时声发射信号变得活跃,岩石内部开始有大量的裂纹产生、扩展和贯通,且降维现象出现在岩石破坏前,所以关联维数的降维现象可作为岩石破坏的前兆特征。 图12 不同参数的关联维数-应变-剪应力曲线Fig.12 Correlation dimension-strain-shear stress curve of different parameters 关联维数在炭质泥页岩剪切破坏全过程中呈现出“升维-动态波动-降维”的演化规律。能量的关联维数比其他参数的关联维数更先进入动态波动和降维阶段,说明关联维数的演化对声发射能量的变化更敏感,且能量的关联维数的降维程度比其他参数更显著,持续时间更长,所以能量关联维数的降维现象更适合用来预警炭质泥页岩失稳破坏的前兆信息。 通过对炭质泥页岩剪切试验,对采集到的声发射数据及其分形特征进行研究,得出以下结论。 (1)声发射活动在炭质泥页岩的不同变形阶段活跃程度不同,在塑性变形阶段最强,其次是压密阶段,最后是弹性变形阶段,且声发射活动在岩石破坏前存在平静期。裂纹在岩样中心产生向四周不断扩张,破坏模式为以剪破坏为主的拉剪复合型破坏。 (2)炭质泥页岩的声发射振铃计数、能量、振幅的时间序列都具有分形特征,振铃计数、能量、振幅的关联维数在破坏全程呈现出“升维-动态波动-降维”的演化规律, (3)声发射平静期可作为炭质泥页岩破坏前兆信息。相比于振幅和振铃计数,关联维数的演化对声发射能量的变化更敏感,且能量的降维现象更显著,持续时间更长,更适合作为炭质泥页岩失稳破坏的前兆特征。 (4)若将工程监测手段与平静期、声发射能量的分形维数演化特征相结合,对边坡岩体失稳预警具有一定应用价值。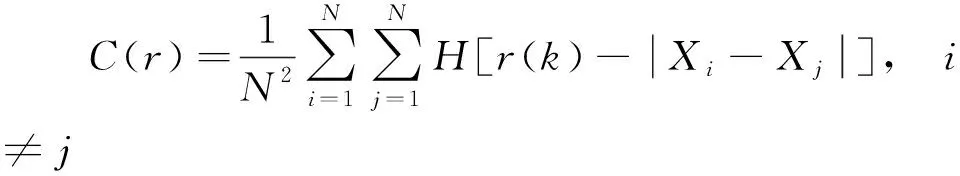



3.2 声发射分形特征的判定和相空间维数的确定

3.3 声发射分形演化研究

4 结论

