基于行政和几何中心的山区聚落空间结构对比:以岷江上游为例

范娜, 田述军, 宋丽君, 杨兰

(西南科技大学土木工程与建筑学院, 绵阳 621010 )

聚落的空间结构是以聚落中心为点,以交通网络为通道连接聚落的各个区域而构成的点、线、面的空间体系。聚落空间结构是一定的生产力水平下,人类认识自然和利用自然的空间分布反映[1],是聚落建立与发展的骨架,受到社会环境和自然环境的影响。因此,研究聚落的空间结构对于加强聚落之间各要素合理流动和促进聚落发展格局调整与优化具有实践意义。

20世纪70年代,分形理论的提出为研究分形几何特征做出重要贡献[2-5]。由于无标度的聚落空间具有的非线性的复杂性,学者们运用分形理论研究聚落的空间结构。鲍紫藤等[6]基于分形理论对茂名聚落分形特征进行研究,并从自然环境和经济等方面构建指标体系,发现聚落空间结构和形态呈现出显著的分形特征。吴映梅等[7]以云南宣威集镇为研究对象,运用分形理论得到其空间结构分形特征明显,且发育受自组织力量影响,为聚落体系优化提供了新视角。庄至凤等[8]采用分形理论方法,对2004—2012年北京市平谷区聚落空间结构演变特征进行分析,并提出了优化空间结构合理策略。梁发超等[9]以厦门市为例,采用分形理论,定量分析了聚落景观空间结构的演变特征。这些学者大多采用聚落行政中心(政府所在地)开展分形理论下的聚落空间结构研究,在地形起伏不大的区域,可利用的土地资源充足,聚落一般以其初始形成区域为中心向周边逐渐扩展和生长,因此,其行政中心与几何中心较为重合。但对于地形起伏较大的区域,可利用土地匮乏,聚落较为分散,其行政中心相对几何中心的偏离较大,采用行政中心进行分形理论下的聚落空间结构研究可能产生较大的误差。

鉴于此,以岷江上游为研究区,采用分形理论分别对聚落行政和几何中心的空间结构特征进行分析,对比两种中心的空间结构差异,揭示不同因素对其空间结构的影响,可为岷江上游地区及类似山区聚落空间格局优化、国土空间规划和乡村振兴提供参考和依据。

1 研究区概况

1.1 研究区概况

岷江上游地位于青藏高原东缘向四川盆地的过渡地带,海拔整体由西北向东南逐渐降低,地形地貌以高山峡谷为主,地形起伏大[10-13]。

岷江上游是藏、羌、回、汉多民族聚居区,形成了西南地区一条关键的民族廊道[12-13],主要包括黑水县、理县、汶川县、松潘县和茂县5个县,其乡镇聚落主要沿河流分布,其中位于研究区东南部的汶川县与成都接壤,受到成都社会经济辐射的影响,经济最发达。岷江上游干线公路主要包括都汶高速、国道213、国道317和省道303、省道202、省道301,受地形条件限制,道路一般都沿河流两岸修建,两者高度重叠(图1)。

1.2 数据来源

结合野外实地调查,收集和整理岷江上游聚落、地形、河流、交通和社会经济等数据,具体如下。

(1)聚落数据。在获取天地图高清遥感影像(分辨率0.5 m)基础上,采用目视解译的方式将聚落建筑数据矢量化,共获得86 814个聚落建筑斑块,如图1所示。

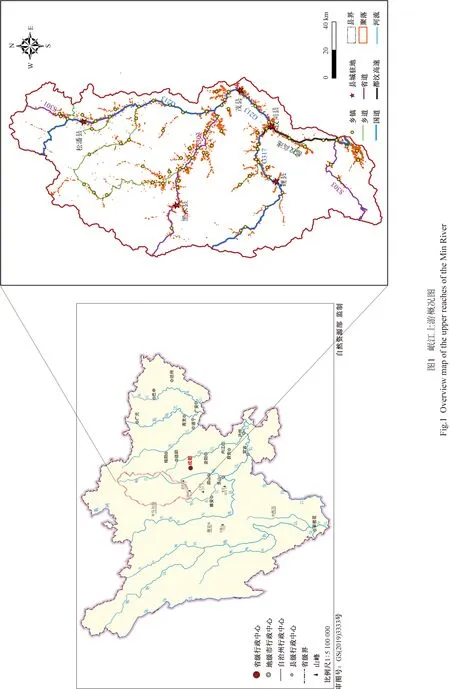
(2)聚落几何中心数据。将提取的聚落建筑矢量数据转换成4 m×4 m的栅格数据,再转换成矢量点,在ArcGIS生成岷江上游核密度分布图,提取出聚落的几何中心,结果如图2所示。

图2 岷江上游聚落几何和行政中心分布图Fig.2 Geometry and distribution of administrative centers in the upper reaches of the Min River

(3)聚落行政中心及其他矢量数据。岷江上游聚落行政中心(乡镇驻地)、行政边界、交通、河流等空间矢量数据来源于国家科技资源共享服务平台——国家地球系统科学数据中心。

(4)地形数据。数字高程模型(分辨率12.5 m)来源于美国国家航天局(National Aeronautics and Space Administration,NASA),经裁剪、拼接,通过ArcGIS可获取研究区海拔高度和坡度等地形数据。

(5)人口和社会经济数据。来源于岷江上游各县统计年鉴。

2 研究方法

分形理论具有自相似和无标度性的特征,分维数能表现分形特征的重要参数,也是刻画分形体量化指标[7,14-15]。分形理论能较好地描述事物的空间状态,且所需变量数少,因此,分形维数被广泛应用于事物空间结构研究中[14]。主要采用城市位序-规模研究岷江上游城镇等级规模分布特征,运用分形理论的聚集维数和空间关联维数分析岷江上游空间集聚和空间关联情况。

2.1 城市位序-规模

城镇等级规模分布具有多边形的分形特征和自相似性。根据城市首位律,一般由2城市指数S2、4城市指数S4和11城市指数S11[8]组成,其计算公式分别为

(1)

(2)

(3)

式中:P1,P2,…,P11为按人口由大到小依次排序的城镇规模。

按照城市首位律的原理,S2为2;S4和S11临界于1。当S2>2时,规模值越大,说明城镇规模分布越集中,高首位城镇发育比较突出,低首位城镇发育不够;当S2<2时,规模值越小,说明城镇规模分布越分散。

2.2 聚集维数

乡镇体系各要素按照自相似的规律,围绕中心首位城镇呈集聚状分布,且各方向均匀变化,则可以利用几何关系测量来确定对应半径与圆周内半径r的乡镇数量N(r)的关系[7-9],可表示为

N(r)∝rD

(4)

式(4)中:D为聚集维数;r为半径;N(r)为以县城驻地为圆心、在半径r内的乡镇数量。

由lnN(r)-lnr的对数进行线性回归,求得聚集分维D。考虑到现实中r的单位,定义平均半径Rs代替r。

(5)

式(5)中:ri为第i个乡镇到首位城镇的距离;S为乡镇数量。

聚集维数D反映了各乡镇从首位城镇密度向周围递减的分布特征,当D<2时,各首位城镇为中心向周边逐渐衰减,各乡镇围绕首位城镇呈聚集分布,吸引力较强;当D=2时,乡镇围绕首位城镇呈均匀分布;当D>2时,各首位城镇为中心向周边逐渐衰增,吸引力较弱。

2.3 关联维数

定义聚落的空间关联函数为[9-10,16-17]

(6)

式(6)中:dij为i、j两乡镇的直线距离;θ为Heaviside函数,可表示为

(7)

如果山区聚落的空间分布是分形的,且具有标度不变性,即N(r)∝rD,D为0～2。

当D趋近于0时,表明乡镇聚落分布高度集中;D趋近1时,表示乡镇聚落在某一条地理线上集中分布,如河流、交通等;当D趋近于2时,说明各乡镇聚落空间均匀分布。分维值D越大,表示各乡镇聚落空间越分散分布,D越小,表示乡镇聚落空间越集中分布,空间之间的作用力也越强,联系越紧密。乳牛维数越接近于关联维数,表示各乡镇之间的交通网络连通性较好[8],故将式(7)的dij改为两地的道路交通距离,结合式(4)测得乳牛维数D′,由此界定牛鸦维数比ρ为

(8)

式(8)中:0.5<ρ<1表明县域内各乡镇之间通达性较好,空间相互连通强,且越趋近1,表示交通连通性越好;当ρ>1或ρ<0.5,说明各乡镇之间交通网络连通性较差[8-9]。

3 岷江上游聚落空间结构分布分形特征

3.1 不同县的首位城镇

研究聚落空间结构的分形特征,需要首先确定不同县域的首位城镇。分别采用式(1)～式(3)计算岷江上游不同县域的2、4、11城市指数,结果如图3所示。除松潘县以外,各县域2城市指数均大于2,4城市指数和11城市指数都趋近1,说明其城镇体系中首位城镇发育较突出,属于首位分布的城镇体系结构。松潘县的2城市指数小于2,4城市指数和11城市指数趋近1,表明松潘县城镇首位城镇发育不明显,城镇规模分布较分散。

图3 县域城市首位度Fig.3 The first degree of county city

对不同县域的各乡镇人口进行统计,计算县域人口数量分布特征,如图4所示。岷江上游80个乡镇人口数量普遍小于5 000人,5个县域人口最多的城镇均为县城驻地(首位城镇),除松潘县县城进安镇人口小于10 000人外,其他县城驻地均大于10 000人,其中汶川县有3个乡镇(威州镇、水磨镇和漩口镇)人口超过10 000人。5个县域的人口数量累计百分曲线中,松潘县相对于其余4个县域较陡,说明其各乡镇人口数量相差较小,城镇人口规模等级较均匀;茂县较缓,首位城镇人口占县域人口的43%,结合图4可知,其2城市指数最大(4.413)。不同县域首位城镇占其总人口的百分比分别为茂县(43%)>汶川县(29%)>理县(30%)>黑水县(23%)>松潘县(12%),这与上述各县域城市位序—规模的特征一致。

图4 县域人口数量累计百分比Fig.4 Cumulative percentage of county population

3.2 基于聚落行政和几何中心的空间集聚特征

3.2.1 聚落空间集聚特征分析

分别计算不同县域聚落行政和几何中心到首位城镇的距离,根据式(5)计算平均半径Rs,统计不同平均半径取值下聚落行政和几何中心的数量S,制作个数—平均半径双对数散点图,并对其直线进行线性拟合,从而得到不同县域的聚集分维值D(斜率),如图5所示。

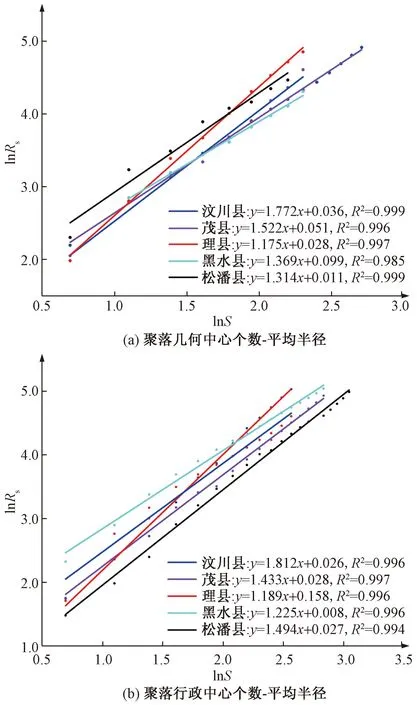
图5 县域城镇空间个数-平均半径双对数散点图Fig.5 Number of county towns-mean radius double-log scatter plot

从图5可以看出,聚落中心点个数与平均半径存在显著的相关性(置信度R2均大于0.99),说明岷江上游乡镇空间结构分形特征显著,可用聚集维数来描述其空间结构。聚落行政和几何中心下,5个县的分维值D均位于[1,2]区间,说明岷江上游聚落在空间上呈聚集特征,以各首位城镇(县城驻地)为中心向周边逐渐衰减。

聚落行政中心下[图5(b)],聚集分维值汶川县>松潘县>茂县>黑水县>理县,汶川县最大(1.812),理县最小(1.189);聚落几何中心下[图5(a)],聚集分维值汶川县>茂县>黑水县>松潘县>理县,汶川县最大(1.772),理县最小(1.175);即聚落行政和几何中心下,汶川县聚集维数最大,理县最小。根据2019年岷江上游5各县的统计年鉴,岷江上游5个县人均GDP数据排名为汶川县(7.05万元)>理县(5.73万元)>黑水县(4.33万元)>茂县(3.63万元)>松潘县(3.36万元),汶川县和理县人均GDP较高。由于理县人均GDP较高,首位城镇(县城驻地)对其他城镇的吸引力较强,使其聚落空间分布最集聚,即分形维数最小。虽然汶川县人均GDP最高,但由于县域乡镇靠近成都都市圈,受成都社会经济辐射影响较大,削弱了首位城镇(威州镇)的吸引力,形成了多中心的分布格局,如县域南部靠近成都的漩口镇和水磨镇核密度较大且人口均超过10 000人(图2)。

3.2.2 聚落行政和几何中心空间聚集差异分析

以聚落几何中心分维值为基准,计算不同县域聚落行政中心分维值的误差,结果如图6所示。同时,根据不同县域聚落几何和行政中心距离制作平均半径箱形图,得到其平均半径均值,计算两种中心平均半径均值的差值,结果如图7所示。行政中心误差大小依次为松潘县>黑水县>茂县>汶川县>理县,两种中心平均半径均值的差值也表现为松潘县>黑水县>茂县>汶川县>理县,表明平均半径是影响行政中心误差的重要因素,平均半径的差异主要来源于聚落行政中心相对几何中心的偏离,因此,采用行政中心进行聚落空间结构研究应考虑这种偏离对研究结果的影响,以研究区松潘县为例,其偏离可以造成分维值最大误差达12.05%。

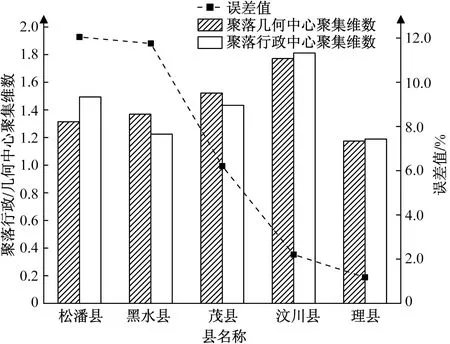
图6 聚集分维误差对比Fig.6 Comparison of aggregate fractal dimension error

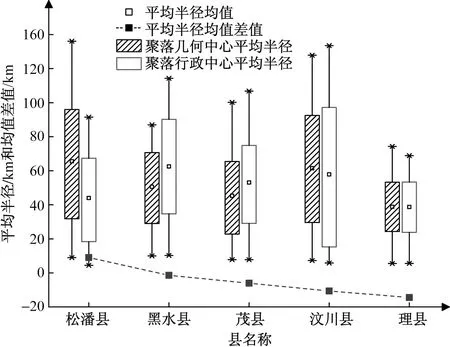
图7 平均半径箱型Fig.7 Average radius box type

3.3 基于行政和聚落几何中心点的聚落空间相关性分析

3.3.1 聚落空间相关性特征分析

在ArcGIS平台中,分别计算两种中心下各县域各乡镇之间的直线距离和实际距离dij,按等间距确定不同r(单位:km),根据式(6)、式(7)确定不同r内的乡镇数量N(r),制作聚落空间分布双对数散点图,并对其进行拟合分析,从而得到不同县域的斜率,即关联维数D和乳牛维数D′,结果如图8所示;根据式(8)计算两种中心下不同县域的牛鸦维数比,并根据关联维数D和乳牛维数D′,制作不同县域的牛鸦维数比分布(图9)。

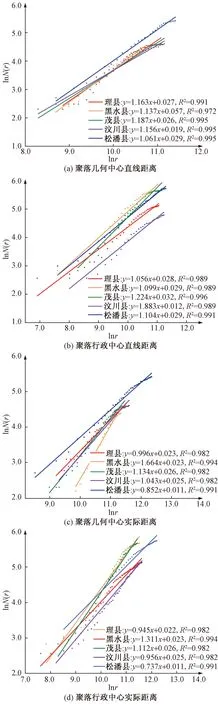
图8 聚落几何和行政中心空间分布双对数散点图Fig.8 Double logarithmic scatter plot of spatial distribution of geometric/administrative centers in the upper reaches

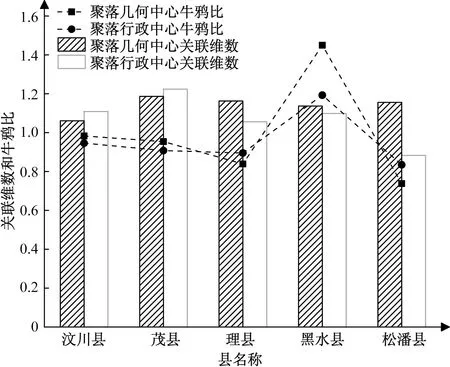
图9 县域关联维数和牛鸦维数比Fig.9 County domain association dimension and cattle and crowration

岷江上游聚落空间分布线性拟合相关性较好,置信度R2均大于0.97(图8),城镇体系空间结构具有明显的无标度特征且城镇空间分形特征明显。两种中心下各县域关联维数最大值为1.224,说明岷江上游城镇空间分布集中,空间相互作用强且联系紧密,并且其关联维数均趋近于1,表明城镇集中分布在某条地理线上,结合图1可以看出,各乡镇聚落沿河流两侧集中分布,河流是影响城镇分布的重要因素。

聚落几何中心和行政中心的牛鸦维数比依次为黑水县>汶川县>茂县>理县>松潘县(图9),两种中心下,除黑水县外,其余4个县牛鸦维数比ρ均位于[0.5,1],说明4个县聚落空间网络连通性较好,空间相互作用强且联系紧密,其中汶川县两种中心的牛鸦维数比最趋近于1,说明汶川县交通通达度最好,乡镇内部各要素联系程度高,这与汶川县靠近成都都市圈,县域内有多条国道和省道,交通最完善相关。而黑水县两种中心的牛鸦维数比均大于1,表明黑水县网络交通体系不够完善,乡镇内部各要素关联度较差,黑水县仅有一条省道(S302),道路等级较低且交通网络不完善,同时,县域地形起伏大,道路曲折,导致交通通达度差。

3.3.2 聚落空间相关性对比分析

以聚落几何中心的关联维数、乳牛维数和牛鸦维数比为基准,计算不同县域聚落行政中心对应的误差。关联维数、乳牛维数和牛鸦维数比误差最大分别为松潘县(30.92%)、黑水县(26.93%)、黑水县(21.54%),误差最小分别为茂县(3.02%)、茂县(1.98%)、汶川县(3.91%)。

岷江上游地处四川盆地向青藏高原东缘过渡交界处,地形陡变,在40～50 km水平范围内海拔从700 m陡变至5 000 m,形成了典型的山地垂直带谱和相应的农业生产方式[18-19]。海拔较高的黑水县、理县和松潘县畜牧业在第一产业中的比重较大(图10),聚落相对分散,使得聚落行政中心相对几何中心的偏离较大,将导致关联维数、乳牛维数和牛鸦维数比产生较大误差,而海拔相对较低的汶川和茂县误差较小(图11)。以黑水县木苏乡为例(图12),木苏乡行政中心位于乡域边缘,与乡域几何中心偏离较大,这种偏离不仅对聚落空间联系程度(关联维数)影响较大,而且对乡镇实际距离(乳牛维数)和交通通达性(牛鸦维数比)也会造成较大影响。可以看出,聚落行政中心相对几何中心的偏移所导致的聚落空间相关性误差在聚落相对分散的高海拔地区尤为明显。

图10 不同海拔农业生产方式Fig.10 Agricultural production at different altitudes

图11 聚落几何和行政两中心误差对比Fig.11 Comparison of settlement geometry and administrative center

4 结论

采用城市位序-规模原理、聚集维数和关联维数方法对岷江上游聚落行政和几何中心的城镇首位度、首位城镇吸引力、城镇相互作用强度和交通通达性等进行分析,揭示其聚落空间结构特征,并对两种中心的聚落空间结构差异进行了对比分析,得出如下主要结论。

(1)岷江上游首位分布城镇体系结构特征明显。岷江上游80个乡镇人口规模普遍小于5 000人,县城所在城镇均为其首位城镇,除松潘县外,人口规模均大于10 000人;县域人口数量累计百分曲线中,茂县最缓,首位城镇人口占县域人口的43%且2城市指数最大,而松潘县最陡,城镇人口规模分布较分散;首位城镇人口占比与县域城市位序—规模的特征一致。

(2)岷江上游聚落空间结构分形特征显著,聚落在空间上聚集分布,并以各首位城镇为中心向周边逐渐衰减,经济是影响聚落集聚特征的重要因素。理县经济较发达,首位城镇吸引力最强,使其聚落空间分布最集聚,即聚集维数最小,汶川县虽然经济最发达,但由于靠近成都都市圈,受成都社会经济辐射影响较大,削弱了首位城镇的吸引力,形成了多中心的分布格局,其聚集维数最大。

(3)岷江上游关联维数和牛鸦维数比所揭示的城镇相互作用强度和交通通达性特征与实际情况一致。岷江上游县域关联维数均小于1.224且趋近1,表明城镇集中分布在某条地理线上,与各乡镇聚落沿河流两侧集中分布一致,河流是影响研究区城镇分布的重要因素。除黑水县外,其余4个县牛鸦维数比均位于[0.5,1],其中汶川县牛鸦维数比最趋近于1,这与汶川县交通网络完善程度和通达性最好一致,而黑水县牛鸦维数比大于1,县域地形高差大,道路曲折,交通网络完善程度和通达性最低。

(4)以聚落几何中心为基准,行政中心造成的聚集维数、关联维数、乳牛维数和牛鸦维数比最大误差分别为12.05%、30.92%、26.93%、21.54%,其最大误差与研究区平均海拔关系密切,平均海拔高的区域,聚落分散,聚落行政中心相对几何中心的偏离较大,误差最大。因此,在采用行政中心研究聚落空间结构(特别是山区)时,应重视其偏离对研究结果的影响。