如何在练习中厘清周长和面积的关系
施志摩

为帮助学生厘清长方形周长和面积概念之间的关系,可以设计以下教学过程。
一、初设冲突,感知本质
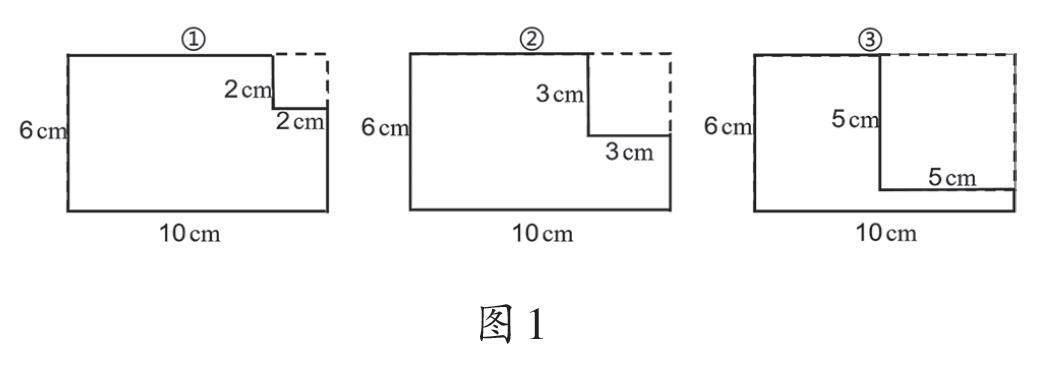
教师出示题目:在长方形中剪去一个正方形。下面三种剪法(如图1)中,哪种剪法所剩部分的面积最小?哪种剪法所剩部分的周长最短?
1.观察猜测。让学生进行观察、猜测,并简单说明猜测依据。
2.操作验证。让学生独立思考、自主探究,并在全班交流,学生整理的结果如表1所示。
3.畅谈发现。
预设1:所剩部分的面积=长方形的面积-正方形的面积,剪去的正方形面积越大,所剩部分的面积越小。
预设2:所剩部分的周长=原来长方形的周长,与剪去正方形的面积大小无关。
二、再设冲突,理解本质
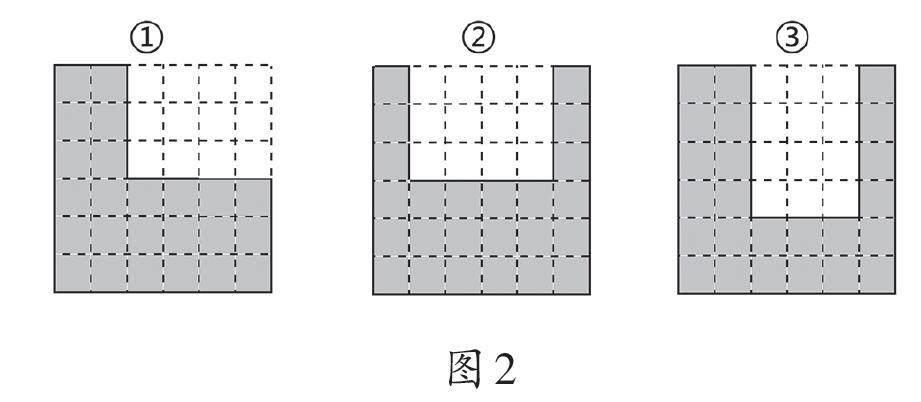
教师出示题目:在正方形中剪去一个长4厘米、宽3厘米的长方形。下面三种剪法(如图2)中,哪種剪法所剩部分的面积最大?哪种剪法所剩部分的周长最长?
1.观察猜测。让学生进行观察、猜测,并简单说明猜测依据。
2.推理验证。让学生自主探究,并在全班交流,学生整理的结果如表2所示。
3.讨论发现。
预设1:剪去相同的长方形,所剩部分的面积相等。
预设2:剪去长方形的位置和方向不同,所剩部分的周长不一定相等。
三、分析异同,感悟本质
教师出示题目:将边长5厘米的正方形剪一刀,变成两个长方形。与原来的正方形相比,这两个长方形的面积之和会变大、变小还是不变?周长之和呢?
1.想象猜测。让学生想象剪开后的图形,猜测这两个长方形的面积之和与周长之和的变化情况,并简单说明理由。
2.自主探究。让学生画图,模拟一种剪法,计算这两个长方形的面积之和与周长之和,完成表3。
3.反馈交流。展示不同学生的作品。
4.动态演示。教师用课件演示如图3所示的裁剪方式(新增线段用红色,其余为黑色),演示多种裁剪的过程。
5.反思发现。
预设:无论怎么剪,这两个长方形的面积之和都等于原来正方形的面积;周长之和比原来的正方形多了两条边长。
上述过程通过不断变换裁剪方式发展学生的空间观念和创新意识,借助计算、说理培养学生的推理意识,在变与不变中,帮助学生更好地理解图形的周长和面积。
(浙江省宁波市北仑区岷山学校)

