思维受阻怎么办

相辉

同学们在解决问题时常常会遇到障碍，使思维受阻，我们可以通过联系实际、从简处入手，运用类比、迁移等方法进行突破。

1.联系生活实际。数学源于生活，应用于生活。因此在解答相关数学问题受阻时，我们可以回到生活中去，动手做一做，动笔画一画，仔细看一看，就会有“山重水复疑无路，柳暗花明又一村”的效果。

例如，给一个长40厘米、宽30厘米、高20厘米的长方体礼品盒捆上彩带，最少需要多少厘米的彩带呢？有的学生认为这就是求长方体棱长的总和，即（40+30+ 20）×4=360（厘米）；还有的学生认为是（40+30+20）×2=180（厘米）。显然这两种算法都是错误的。那怎么办呢？我们不妨动手用绳子扎一扎，捆一捆。发现牢固而又节省彩带的捆法是2条长、2条宽和4条高的和，就是（40+30）×2+20×4=220（厘米）。

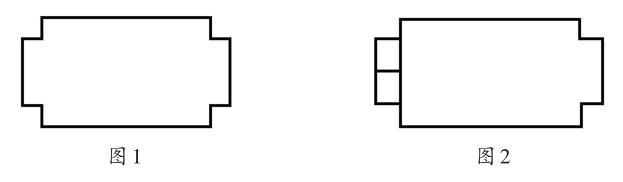
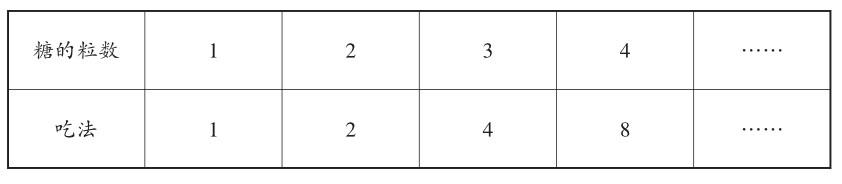
再如，把一块长20厘米、宽16厘米的长方形铁皮，从角上剪掉边长是4厘米的正方形后，焊接成一个无盖的长方体，怎样才能使它的容积最大？（铁皮厚度忽略不计）多数学生受思维定式的影响，认为是剪去四个正方形的角（如图1），容积是（20-4-4）×（16-4-4）×4= 384（立方厘米）。但这样焊接，容积并不是最大的。到底该怎样做呢？通过动手剪一剪、拼一拼或画一画，我们发现：剪去2个角，然后拼到另一侧，材料一点儿不浪费，这样容积才最大（如图2）。容积为（20-4）×（4+4）×4=512（立方厘米）。

2.从简单处入手。有些题目无法直接求出答案，我们需要从最简单处入手，找出规律，然后运用。例如，有6粒糖，每次至少吃1粒，吃完为止。问有多少种不同的吃法？乍一看无从入手，我们可以从最简单处入手。假设只有1粒糖，就只有1种吃法；有2粒糖，就有（1，1）、（2）2种吃法；有3粒糖，就有（1，1，1）、（1，2）、（2，1）、（3）4种吃法；有4粒糖，就有8种吃法……列表可以发现每多1粒糖，后一个的吃法总是前一个的2倍。所以5粒糖就有8×2=16（种）吃法，6粒糖就有16×2=32（种）吃法。

3.借助轉化的策略。思考问题受阻时，我们可以通过转化，找到与已有知识间的联系，进而找到突破口。例如，如何判断一个数是不是6的倍数？因为6= 2×3，所以可以用求这个数是不是2和3共同的倍数的方法来验证。