多级变孔径孔板装置水力特性研究

王立强 孙正新 王卫东

(1.中核新华黄龙抽水蓄能发电有限公司, 甘肃 天水 741000;2.新疆兵团水利水电工程集团有限公司, 新疆 昌吉 830000;3.兰州新区现代农业投资集团有限公司, 甘肃 兰州 730000)

1 概 述

在大型水利工程中,国内外很多大坝高度都接近300m,如此高的大坝下泄水流时会携带高速流体,若不加处理,高速流体会导致大坝本身安全性降低及泄水建筑物遭受空蚀空化破坏[1-2]。如美国包尔德坝东岸泄洪隧洞,由于高速水头的作用使隧洞转弯处的混凝土被空化剥蚀,产生一个大坑;又如我国某溢流坝的导流底孔[3],因汛期来不及堵塞,超过设计水头泄洪130天后,产生严重的空化破坏,使孔顶及两个墩墙表面混凝土被剥蚀。所以高水头泄水建筑物的空化现象是值得重视的问题。而在小型管道输水工程中[4-5],有一些输水管道由于地形地貌条件的影响,当输水管道的起始点与终点高程相差较大时,若不加处理,到达终点的水流具有较高的流速,高速水流将会冲刷管壁[6],导致工程本身安全性降低。所以为了保护管壁、大坝泄洪洞及下游设备的安全,非常有必要研究一种有效而且经济适用的消能降速模型。多级孔板消能降速模型具有结构简单、装卸方便、可操作性强等特点,被广泛地应用在水利工程中。

在国内研究中,我国首次提出采用孔板模型的是黄河小浪底工程,该工程将导流洞改为永久的泄洪洞,林秀山等对泄洪洞内的流态、流速以及压力变化规律进行了试验研究[7];碧口水电站的排沙洞采用两级等直径孔板组合的结构,对实际数据分析研究发现,对于高含沙水流的消能效果显著,同时可以避免排沙洞被高速水流空化空蚀;艾万政等采用RNGκ-ε模型对孔板回流区在不同的影响因素状态下作了详细的分析,孔径比增大,回流区长度减小,回流区长度与孔板厚度呈负相关[8-10];哈焕文等对泄洪洞两级孔板宣泄含沙水流消能及空化特性的原型进行了试验研究[11];汤建明采用Realizableκ-ε模型对多级减压孔板水力特性进行了研究[12]。在国外研究中,Johnson等研究了等径孔板螺旋流的分布状况,研究表明螺旋流流场中压力最低位置位于管轴中心处,且压力沿着管轴向径向呈增大趋势[13];Jeanpierre进行了螺旋形涡室模型结构的研究与探讨[14];Fratino等的研究发现:随着观测点沿着管道向下游移动,螺旋流切向速度逐渐降低,并向管道中轴线处逐渐偏移[15]。

综上所述,以上学者对多级等直径孔板的流态、流速变化规律的研究较为充分,而对多级变孔径孔板的流态、流速变化规律研究甚少,特别是对多级变孔径孔板空化现象的研究极少,所以多级变孔径孔板的空化现象是一个值得研究的水力学问题[16-17]。本文通过数值模拟研究计算分析多级变孔径孔板在不同雷诺数、扭转角、收缩角下对孔板空化特性及流场特性的影响。

2 模拟方法

2.1 几何模型

图1为多级变孔径孔板模型的平面图与三维模型图,几何模型主要由输水管道、扩大的孔板室段、孔板组合段三部分组成。图中输水管道的直径为d,扩大的孔板室段的直径为D,做扩大的孔板室段的目的是防止孔板段过流面积突减造成孔板前形成严重的壅水现象。为确定多级变孔径孔板消能模型的几何尺寸,模型中令输水管道的直径d为100mm,并将模型其余的尺寸以d相关的无量纲表示。d/Z为输水管道沿水流方向Z的长度,d/Z=2400mm,即管道直径d沿着水流Z轴方向的试验界道长度为2400mm。孔板组合段位置在9.5d处,孔板室直径为1.5d,孔板厚度为0.1d,孔板间距为0.06d,多级变孔径孔板的块数为3块,输水管道无坡度。

对多级变孔径孔板段的每块孔板直径尺寸及收缩角的大小进行参数化设计,在进行参数化设计时,按孔径由小到大依次令第一块孔板孔口半径为R1,第二块孔板孔口半径为R2,第三块孔板孔口半径为R3,第n块孔板孔口半径为Rn,相邻孔板之间的距离为L,每块孔板的厚度为H,令孔板组合段的收缩角为α。将多级孔板组合段的三维模型及平面图(见图2)进行局部放大并进行参数化计算,得到R1、R2…Rn与L、H、α的关系。

图1 多级变孔径孔板模型的平面图与三维模型图

图2 多级孔板组合段的三维模型及平面图

由多级变孔径孔板平面图进行数学计算推导:

(1)

由式(1)得

(2)

带入式(2)得

(3)

2.2 模拟计算方案

为了研究多级变孔径孔板空化特性及流场特性,本模拟方案选取3块孔板,每块孔板的厚度为0.1d,相邻孔板的间距为0.06d,规定孔板R1的尺寸为15mm,孔板的收缩角度α为15°、30°、45°,通过规定的R1及收缩角度由式(3)计算得到在不同收缩角下的R2、R3。模拟选取的流量为20m3/min、25m3/min、30m3/min、35m3/min(所对应的雷诺数分别为70297、87128、104950、122772),扭转角分别为0°、6°、12°,通过改变雷诺数、扭转角及收缩角确定模拟方案共36组,并对每组方案孔板的空化数及流场特性进行数值模拟计算分析。具体的模拟方案见表1。

2.3 网格划分及无关性验证

本模拟方案共36组,选取方案C6进行网格划分及无关性验证。网格划分采取非结构化四面体网格,将模型进行分区,定义不同尺寸的网格,并对孔板组合段进行局部加密,共选择了3种网格划分方案。图3为152万、306万、480万网格下管道压强沿程变化的模拟值与试验值之间的对比(试验实测值所选取的断面为0m、0.35m、0.75m、1.05m、1.4m、2.1m、2.4m)。由图3可以看出,网格数306万和480万与实测值吻合良好。综合考虑模拟结果的准确性、计算量以及计算效率,最终选择306万网格数的模型,且所对应的模型网格划分见图4。

表1 模拟方案

图3 管道断面压强的数值模拟与试验结果对比

图4 扭转角6°、收缩角45°模型对应的网格划分

2.4 计算模型与边界条件

本模拟最小雷诺数70297大于8000～12000,所以管道中的流体流动状态为湍流。由于流体在不同方案下,在孔板段容易形成扩散螺旋状孔口,导致孔板段的水流既形成螺旋流又形成扩散流,使水流内部产生强烈的紊动、混掺、碰撞。为了让模拟计算结果具有较高的精度从而达到接近真实结果的目的,本计算模型采用Realizableκ-ε湍流模型,因为Realizableκ-ε湍流模型能够满足对雷诺数应力的约束条件,因此可以在雷诺数应力上与真实湍流保持一致,它可以更精确地进行在旋流中的计算、带方向压强梯度的边界层计算和分流计算等,使计算结果更符合真实结果。控制方程根据有限体积法进行迭代求解,速度压力耦合采用PISO算法,Realizableκ-ε湍流模型的控制方程包括紊动能方程(κ-方程)和紊动能耗散率方程(ε-方程)[18],其具体的表达式如下:

κ-方程:

(4)

ε-方程:

(5)

其中:

式中:uj为速度分量;xj为坐标分量;μ为动力黏度系数;μt为涡黏度;Gκ为速度梯度产生的湍动能;σκ、σε为κ-方程和ε-方程的湍流Prandtl数,σκ=1.0,σε=1.2;C1ε、C2ε为经验常数,C1ε=1.44,C2ε=1.9。

3 模拟结果及分析

3.1 空化特性分析

空化现象是液体在流动过程中,由于压强突然低于某一临界值,液体突变为气泡的状态。当这些气泡在流动时突然发生溃灭时,会释放出大量的热能与压能,与管道的管壁相互挤压,会对管道内壁造成空蚀破坏[19]。本文所涉及的多级变孔径孔板模型在恒定流量与温度下,由于多级变孔径孔板模型流体流经孔板段时,会使流体速度的大小与方向发生突变,流体在孔板后出现与管壁分离的现象,从而产生大量旋涡,在局部区域引起压强突降,导致出现负压区形成空化。在实际工程中,在管道中持续的空化现象会对管道内壁形成空蚀,引发安全问题,故对空化特性的研究在实际工程中是必不可少的[20]。一般用空化数σ表示流体的空化特性,空化数越大,管道内越不容易出现空化现象,管道内壁的抗空蚀能力就越强。空化数σ的表达式为

(6)

式中:Pv为该温度下的饱和蒸汽压强;V为水流沿管道断面中心点的流速;ρ为水的密度;P为水流沿管道断面中心点的压强。

对多级变孔径孔板在同一扭转角、同一收缩角及不同的雷诺数(对应的方案分别为B5、B6、B7、B8,C1、C2、C3、C4)下;对同一扭转角、同一雷诺数及不同的收缩角(对应的方案分别为A4、B4、C4,A9、B9、C9)下;对同一收缩角、同一雷诺数及不同的扭转角(对应的方案分别为C3、C7、C11,B2、B6、B10)下通过式(6)计算分析空化数沿程变化情况,见图5。

图5 不同方案下空化数沿程变化情况

分析图5可知:ⓐ在不同的雷诺数、收缩角及扭转角下空化数沿程分布的规律基本保持一致;ⓑ在同一收缩角、扭转角及不同的雷诺数下,在孔板组合段之前空化数随雷诺数的增大而增大,而在孔板段组合段之后空化数随雷诺数的增大而减小;ⓒ在同一雷诺数、扭转角及不同的收缩角下,收缩角的改变对空化数变化的影响并不大,空化数沿程变化基本一致,且在1m附近达到最小;ⓓ在同一雷诺数、收缩角及不同的扭转角下,扭转角的改变对空化数变化的影响并不大,空化数沿程变化基本保持一致,且在1m附近空化数达到最小。

综上所述,多级变孔径孔板模型扭转角及收缩角对空化数变化的影响并不大,而雷诺数改变对空化数变化的影响较大,即雷诺数的改变使管道空化的可能性增大。

3.2 流态分析

本文多级变孔径孔板模型管道内流体流动状态为湍流,由于孔板具有一定的扭转角度,即流体经过孔板后会形成螺旋流,内部的流态会非常复杂,试验无法测定其具体流态及运动要素的变化规律,所以下文为探究管道内流体流态的变化规律,对其雷诺数为104950,收缩角为45°,扭转角分别为0°、6°、12°(对应的方案为C3、C7、C11)方案下的模拟结果进一步分析,即先对三种方案下孔板后的流体流线图进行分析,见图6。

图6 不同方案下的流线图

分析图6可知:ⓐ每种方案下由于孔板段的存在,在孔板段前后就会形成突缩突扩的水流,且部分流体在突扩后沿管轴继续流动,而在孔板后与管壁接触的流体由于速度大小与方向发生突变导致此处流体的流线发生改变形成涡流;ⓑ分析三种方案的流线图可知:方案C11产生的螺旋流最强烈,方案C3几乎不产生螺旋流,这是由于方案C3孔板的扭转角度为0°,属于多级孔板射流,即在孔板后流体的流线几乎保持一致;方案C7、C11只改变孔板的扭转角度,随着孔板扭转角度的增大,孔板段流体的切向、轴向速度也增大;流体的切向、轴向速度越大,形成的螺旋流也就越明显。

综上所述,在同一雷诺数及同一收缩角下,变孔径孔板扭转角越大,形成的螺旋流越明显。

3.3 流速分析

为进一步探究多级变孔径孔板模型内流体速度的变化规律,从上面三种方案流体流线图分析可知,方案C11流体流线图最复杂,即对该方案下的流体进一步进行断面流速分析,获取该方案下模型在断面Z=0.35m、Z=0.75m、Z=1.05m、Z=1.4m、Z=2.1m、Z=2.4m中心线上流体轴向、切向、径向的速度数值,并截取Z=0.75m、Z=1.05m、Z=1.4m断面上流体速度矢量图进行分析。截面分布图、三相速度变化图、截面速度矢量图见图7～图9。

分析图8和图9可知:

a.Z=0.35m截面靠近管轴中心处的流速较大,且速度保持稳定;而靠近管壁处的轴向速度逐渐减小且出现负值,直到管壁处速度减小为0,这是由于该截面刚好是管道突扩段,在突扩段的直角区域内流体速度大小与反向发生突变,导致在该区域内流体形成回流,即速度变为负值,而靠近管壁流体由于黏滞力的作用导致管壁处速度为0。

b.Z=0.75m截面处流体速度较Z=0.35m截面有所降低且无负值,这是由于该截面处于孔板前端,孔板段的存在会使流体过流面积减小,在孔板前就会形成壅水现象导致流速有所降低。

图7 截面分布图

图8 不同测压断面三相速度变化图

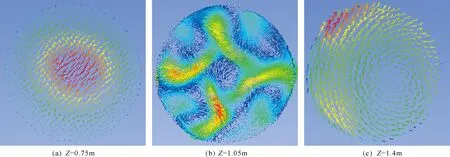
图9 不同测压断面速度矢量分布图

c.Z=1.05m截面处流体的轴向、切向、径向速度呈现波动性变化,且最大轴向速度较Z=0.35m、Z=0.75m截面处最大轴向速度扩大了2倍,靠近管壁处速度出现负值。出现负值是因为孔板后端突扩的部分流体会在管壁附近形成回流。由Z=1.05m截面速度矢量图可知:该截面处于孔板后端,在孔板及扭转角的作用下流体速度的大小与方向发生突变,切向速度增加,使靠近壁面的流体形成四股螺旋状的流束并沿管道继续向前流动。

d.Z=1.4m、Z=2.1m、Z=2.4m截面处流体的轴向、径向、切向速度逐渐趋于稳定。由Z=1.4m截面速度矢量图可知:流体在流动的过程中由Z=1.05m截面的四股螺旋状流束逐渐融合为一股稳定的螺旋状流束,因此在Z=1.4m、Z=2.1m截面处的流速有所降低。在Z=2.4m截面处流体的流速增加,这是由于Z=2.4m截面位于管道突缩段,流体从管径大的管道经过管径小的管道必然会导致流速增大。

综上所述,变孔径孔板的存在对管道内流体的轴向、切向、径向速度大小与方向的影响较大,在孔板段前流体速度基本保持一致,而在孔板后流体的流速突增为孔板前的2倍,之后由于螺旋流强度的减弱,流体流速逐渐减小并趋于稳定。

4 结 论

a.多级变孔径孔板装置的扭转角及收缩角对空化数沿程变化的影响并不大,而雷诺数的改变对空化数沿程变化的影响较大,在孔板组合段之后空化数随雷诺数的增大而减小,即雷诺数的改变使管道空化的可能性增大。

b.多级变孔径孔板装置在同一雷诺数及同一收缩角下,孔板的扭转角度越大,流体的轴向、切向速度也就越大,在孔板后形成的螺旋流流态也就越明显。

c.多级变孔径孔板的存在对管道内流体轴向、切向、径向速度大小与方向的影响较大,在孔板段前流体速度基本保持一致,而在孔板后流体最大轴向速度达到孔板前最大轴向速度的两倍,在此区域内形成四股强烈的螺旋状流束,之后由于切向速度逐渐趋于稳定,四股螺旋状流束逐渐融合为一股稳定的螺旋状流束并沿管道继续向前流动。