基于安全裕度的网联自主汽车换道行为风险量化及动态平衡模型
陈意成, 曲大义, 邵德栋, 杨子奕
(青岛理工大学交通运输工程系, 青岛 266520)
在智能网联环境的促进下,自动驾驶技术得到了空前的发展,提高了交通流的安全性,但交通安全问题同样不能忽视。针对车辆事故制定各种预防策略,首先需要准确评估车辆周围的潜在风险。但是在传统的交通环境中,驾驶员只能接收到很少的信息,而且其中大部分是不准确的,例如与周围车辆的距离,前方车辆的速度等。不同驾驶员具有不同的驾驶风险感知能力,增加了风险评估过程中的不确定性。然而,在CAV(net-connected autonomous vehicles)环境中,车辆可以接收各种准确的动态信息。重要的是,车辆可以感知一些人类驾驶员无法直接感知的信息,如周围车辆的加速度和转向角等。车辆可以接收多种运动信息,并结合实际交通环境和驾驶要求,对所需的运动行为提供反馈。在这种情况下,一些传统的交通风险指标已经过时,无法满足CAV环境中更准确地换道风险评估的要求。因此,建立符合CAV特性的交通风险指标成为评估换道行为风险的重点。
中外学者在驾驶风险指标和换道模型方面进行了相关研究。Ozbay等[1]提出的事故指数可以描述事故碰撞中涉及的动能影响,同时也可以定义事故的严重程度。Wang等[2]建立人车道路闭环系统的“车辆安全场”统一模型,为复杂交通环境下的驾驶风险提供了一种有效的方法。许伦辉等[3]以最小安全距离作为换道目标,建立双车道环境下最小安全距离换道模型。贾彦峰等[4]建立安全势场模型,系统地刻画网联自动驾驶车辆在行驶过程中面临的安全风险。郭海兵等[5]建立Logit模型定量分析驾驶人换道行为决策过程。曲大义等[6]从博弈论的角度研究自动驾驶车辆换道的交互性,合理地展示了自动驾驶车辆的换道特性。
综上可以,前人从不同角度对换道风险评估指标研究做出了巨大贡献,但单一评估指标适用范围有限,很少有人关注综合评估方法,大多数研究根据历史轨迹数据集在变道后进行短期评估,缺乏对换道风险的实时量化。鉴于此,提出一种换道瞬时风险量化模型,基于车辆实时运动信息综合评估换道风险,进而做出合理的安全判断,以便预警。所提模型通过故障树分析法整合分别由碰撞时间和安全裕度推导的时间风险系数和空间风险系数,进行时空融合的风险评定量化,以判断车辆是否处于安全变道状态,并对本次换道可能存在的风险进行预警控制,进一步使换道风险处于动态平衡的可接受范围内。在目前复杂的智能网联道路环境下,保障自主驾驶车辆队列的稳态运行。为后续网联新型混合车流的车辆换道轨迹规划相关研究提供理论基础。
1 风险平衡理论描述
根据风险平衡理论[7],驾驶员可以根据经验感知风险信号,并通过特异性的驾驶行为补偿当前的感知风险,使感知风险恢复至可接受风险的范围内,从而达到一种风险平衡状态。其所采取的驾驶行为,(例如与前方车辆大于或小于一定距离时,驾驶员会响应地加速或者减速以调整与前方车辆的距离)很大程度上取决于感知风险和可接受风险之间的差异。然而,如果需要量化这种差异,则需要确定一种风险感知指标。该指标不仅包括对当前风险水平的主观感知,还包括客观感知。换言之,此量化指标的影响因素在考虑驾驶员特异性的同时,还应该结合当前道路交通流的实际运行状态,以确保其具有动态评估当前风险水平的能力。
根据风险平衡理论[7],驾驶员通过增加冒险行为来抵消其在安全感知方面的收益,以维持风险水平的平衡。但换道行为与跟驰行为不同,前者本身具有一定的基础风险水平,可以视为一种冒险行为。同时应该区分主动换道与被迫换道,因为主动换道是一种驾驶员自发性寻求高安全收益的行为,而不是迫于突发的交通状况,相比较被迫换道,驾驶员具有更大的可接受风险范围。
在交通风险量化的相关研究中,碰撞时间(time to collision,TTC,记为TTC)是一种经典的风险指标,定义为:以当前两辆车的相对速度行驶,将会发生碰撞的时间,数值越大表示越安全。与其他传统风险指标相比,TTC具有计算相对简单而且广泛应用的优势。目前许多车辆防撞系统或驾驶员辅助系统都已经将TTC作为重要的安全指标。TTC可以从主观风险的角度解释驾驶员如何识别风险信息。但是仅使用TTC不足以评估所有交通情况的客观风险水平。例如,企图换道的车辆与目标车道的后车之间的速度差非常小时,尽管两辆车之间的相对距离很小,但此时TTC却非常大。TTC可以用来量化大多数的情况的交通风险,并用来研究风险水平的变化趋势,但是可能由于上述情况导致驾驶员处于更高的风险之中。
为此,在风险平衡模型中提出的瞬时风险系数,在使用安全裕度评估主观风险基础上,综合时间和空间风险,使得评价指标同时具有评价主观风险与客观风险的能力。
2 基于安全裕度的风险量化分析
对交通事故进行预防,必须了解目标车辆在给定的换道条件下是否处于危险状态。在交通密度较高的情况下,目标车辆企图换向更高速车道,通常会遇到被几辆车包围的情况。这就要求驾驶员在变道时应该更加关注交通环境以及周围车辆的动态,以保持安全的车距和速度,否则就有可能发生碰撞或者事故。由于不同的道路环境、车流状态与驾驶员特性,使得安全的车距和速度一直处于一种动态变化状态。为判断车辆是否处于安全状态,以及进一步量化风险,引入安全裕度(safety margin,SM)。Nilsson[8]将其描述为“令驾驶员感到威胁的距离”,安全状态判断函数为
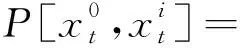
(1)
在评估变道风险的过程中,应首先计算目标车辆(subject vehicle,SV)与每个交互车辆之间的SM。但是车辆之间可能存在各种位置关系。如图1所示,与前车(front vehicle in the current lane,FV)和目标车道前车(preceding vehicle in the target lane,PV)相比,SV位于后方位置,而与当前车道后车(rear vehicle in the current,RV)和目标车道后车(lag vehicle in the target lane,LV)相比,SV位于前方位置。可以用F和R分别表示前方车辆和后方车辆,来解释复杂的相对关系。依照上述定义,SV与周围每辆车的SM可描述为
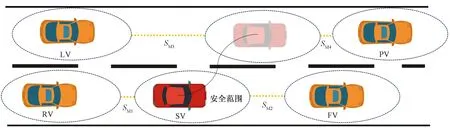
图1 网联混合交通流车车交互关系Fig.1 Vehicle-vehicle interaction in networked hybrid traffic flows

(2)
DR(t)=xF(t)-xR(t)-LF
(3)
式中:VR(t)为在t时刻后车的速度;VF(t)为在t时刻前车的速度;τ1为驾驶员响应时间;τ2为制动系统响应时间;aR(t)为t时刻后车的加速度;aF(t)为t时刻前车的加速度;DR(t)为t时刻两辆车之间的相对间距;xF(t)、xR(t)分别为前车和后车在t时刻的位置;LF为前车的长度;下标F和R分别为前方车辆和后方车辆。
当车辆采取制动措施时,其加速度会受到附着系数的影响。附着系数又受到速度、载荷和路面性能等参数的影响。附着系数的极值通常为0.1(结冰路面)~0.9(沥青混凝土路面)[9]。《道路通行能力手册》建议“乘用车的起步加速度在0.9~3.9 m/s2范围内,减速度在2.1~7.8 m/s2范围内[10]”。结合大多数轮胎磨损、路面状况和Vangi等[11]的测试数据,模型中的加速度见式(4)。
aR(t)=aF(t)=0.75g
(4)
式(4)中:g为重力加速度。
制动系统响应时间也因制动踏板的力和速度的差异而有所不同。液压制动器的响应时间一般小于气压制动器。在分别研究了配备防抱死制动系统(anti-lock braking system,ABS)前后的车辆制动参数后,Sokolovskij[12]研究发现,日本和西方国家大多数车辆的减速时间小于0.2 s,并保持在0.1~0.2 s的范围内。在紧急情况下,驾驶员可能会快速而有力地踩制动踏板。因此将τ2设为0.15 s。
关于驾驶员的感知制动反应时间,Gardoni等[13]研究发现,当驾驶员完全了解制动信号出现的时间和位置时,在识别信号后0.70~0.75 s内将脚从油门移动至制动踏板;对意料之外但常见的信号(如前车的刹车灯)的响应时间为1.25 s;而对于完全意外的事件,为1.5 s。这些时间在一定程度上还受到其他因素的影响,包括驾驶员的年龄、性别、认知能力和压力等。本文模型将τ1设置为1.25 s。
因此安全裕度简化为
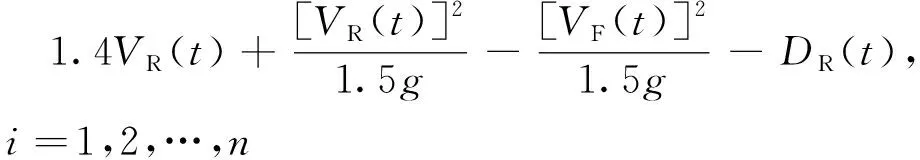
(5)
3 基于故障树分析的换道行为时空风险平衡模型
如果具有换道需求的目标车辆在当前交通条件下存在潜在碰撞风险,则需要对的时间和空间风险进行详细评估,得出瞬时风险系数,为风险预警做准备。故障树分析法作为安全系统工程中分析风险的重要方法,是一种逻辑演绎体系的评价方法,既可以是定性的,也可以是定量的,通常被用于分析整个系统的故障与每个部分故障之间的关系(图2)[14]。
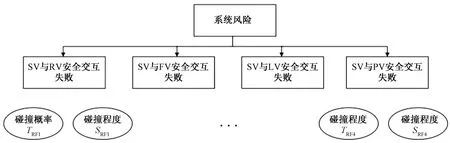
图2 故障树分析法流程Fig.2 Fault tree analysis process
对于换道行为,系统风险定义为目标车辆与周围车辆安全交互失败。当目标车辆移动到不同位置时,它与交互车辆的交互行为存在差异。因此,根据目标车辆与车道线的相对位置关系,瞬时风险系数有两种计算方式:①在目标车辆完全越过车道边线之前,瞬时风险系数最多受附近4辆交互车的影响,在这种情况下,可以通过计算4个部分的故障系数得到;②一旦目标车辆完全越过车道边线,瞬时风险系数就只受目标车道上的PV和LV影响,在这种情况下,可以通过计算最多两个部分的故障系数得到。
在使用故障树分析整体瞬时风险系数之前,需要确定每个部分的风险系数。而对于每个部分的风险系数,通过碰撞严重程度(spatial risk factor,SRF)和碰撞概率(temporal risk factor,TRF,记为TRF)综合表示。
TRF是根据TTC推导,旨在描述当目标车辆处于不安全的道路状况时,量化发生碰撞的可能性的指标[15]。采用故障树分析法量化SV在时间t处的瞬时风险系数γ确定过程如下。
(6)
λi(t)=TRFi(t)SRFi(t)
(7)
(8)

(9)
(10)
(11)

目标车辆的换道风险与交互车辆是否为自动驾驶车辆(autonomous vehicles, AV)有很大关系。由于AV的运动状态是稳定且可预测的,当目标车辆的相邻车辆为AV时,此时换道的风险是可控的。但手动驾驶车辆往往会由于误判、生理和环境等因素出现方向偏离和突然减速的情况,不可控风险程度较高。而且介于完全自动驾驶受限与技术、政策、经济、法律和伦理等因素,无法形成规模化应用。本文模型更适合装载高级驾驶辅助系统(advanced driver assistance system,ADAS)的目标车辆处于周围为纯手动驾驶车辆情况下的换道场景。
本文模型根据周围交通状态,通过计算安全裕度,综合故障树分析,推导变道的时间和空间风险,进行时空融合的风险评定,判断目标车辆是否处于安全变道状态,并对在本次换道中可能存在的风险进行预警,具体流程如图3所示。然而,风险评定是一个动态的过程,将伴随着动态交通环境的演变趋势同时进行优化,在目标车辆驾驶员接受本模型提供的换道预警信息后,有利于避免发生危险碰撞或严重碰撞,并对提高当地交通流的安全性和可靠性有极大帮助。

图3 风险量化模型Fig.3 Risk quantification mode
4 模型仿真验证分析
4.1 仿真环境
为了验证本文模型的可行性,采用SUMO(simulation of urban mobility)微观交通流模拟程序。模拟道路为双车道城市道路,总长度为1 500 m。限速设置为60 km/h。采用IDM(intelligent driver model)车辆跟驰模型和LC2013换道模型来模拟车辆微观驾驶行为。车辆输入包括SV、PV、FV、RV、LV。分别以45 km/h的恒定速度,37、43、50、60 km/h的初始速度行驶,由于使用的模型参数都是内置在SUMO中的标准参数,无需进行其他更改。
4.2 仿真过程与结果
根据Lee等[16]对换道碰撞紧迫性的划分,设计3组平行实验,如图4所示。A组控制SV(蓝色车辆)在与LV(粉色车辆)的TTC=5.5 s发起超车动作,B组控制SV(绿色车辆)在与LV的TTC在(3.0,5.5)范围内发起超车动作、C组控制SV(红色车辆)在与LV的TTC在TTC=3.0 s时发起超车动作。

图4 仿真实验Fig.4 Simulation experiment
图5中所示范围边界分别表示SV开启转向灯至车身完全越过车道边线的时刻,并分别对应图6中的峰值与突变处。结果表明,驾驶员在目标车道后方车辆的TTC=5.5时采取换道措施,瞬时风险系数γ将达到0.6;驾驶员在与目标车道后方车辆的TTC处于(3.0,5.5)范围内采取换道措施,瞬时风险系数γ将始终保持在0.4以下;可初步判定瞬时风险系数阈值。
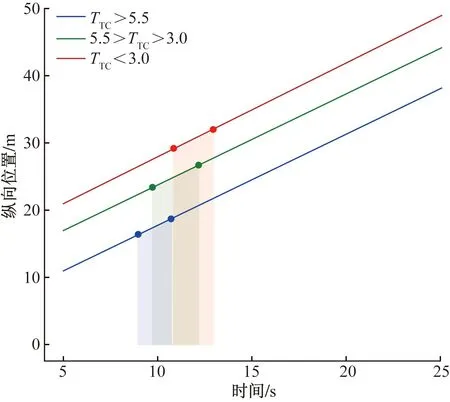
图5 SV纵向位置Fig.5 SV vertical position
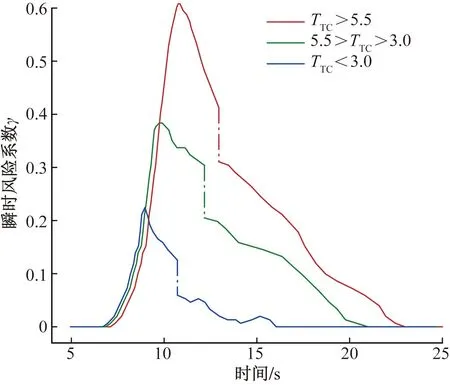
图6 SV瞬时风险系数变化Fig.6 SV instantaneous risk factor variation
为更客观合理地对提出的量化平衡模型进行评价,得到更精确的测试结果,将全部车辆的固定速度限制解除,控制SV在瞬时风险系数处于[0.2,0.4]范围内开始采取变道措施,重复实验10次,每个实验持续时间为20 s。最终生成201个数据段。
当使用TTC指标量化交通风险时,越小的值表示风险越高。采用TTC的倒数来确保数值与交通风险的正相关性。
试
对于图8中的瞬时风险系数γ,控制前和控制后的平均值分别为0.246 6和0.195 1。应用相同的MWW方法,结果也显示处于在0.5%置信水平(U=90 601,r=1.00),这表明所提出的瞬时风险系数也可以很好地评估后续车辆的驾驶风险。

图8 瞬时风险系数统计结果Fig.8 Statistical results of instantaneous risk factor

图9 风险控制前SV与LV加速度Fig.9 SV and LV acceleration before early risk control
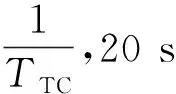

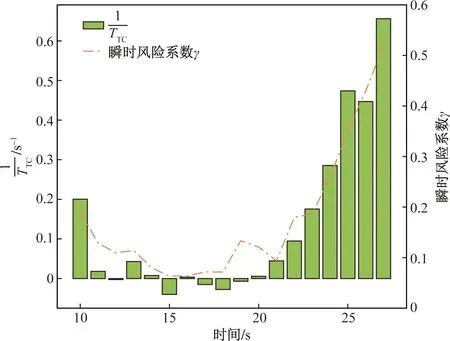
图10 风险控制前与风险系数 and risk factor before early risk control
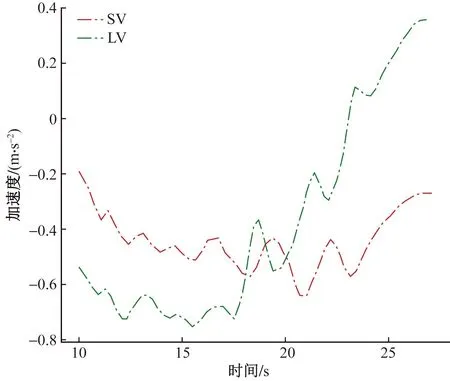
图11 风险控制后SV与LV加速度Fig.11 SV and LV acceleration after early risk control
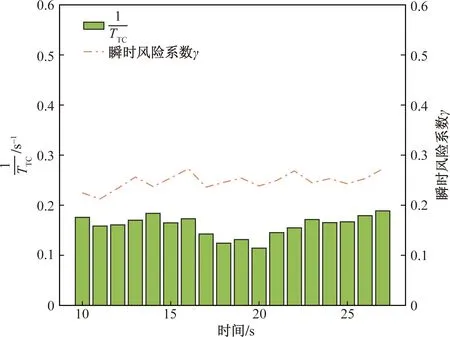
图12 风险控制后与风险系数 and risk factor after early risk control
5 结论
基于安全裕度理论,结合风险平衡思想,运用故障树分析法对换道行为风险进行了量化控制,建立网联新型混合车流的车辆换道行为风险量化及动态平衡模型。从时间和空间两方面动态平衡当前交通状况的换道风险,以便精确识别不适合变道的危险交通状况。得出如下结论。
(2)本文模型使驾驶风险得到了有效控制的同时,交通流的稳定性得到了较大提高,促进未来CAVs环境中CAV队列的形成,从而提高交通容量和交通效率。
(3)为后续网联新型混合车流的车辆换道轨迹规划相关研究提供理论基础。需要在未来的研究工作中考虑驾驶风格和车辆之间的相互作用等关键因素。

