基于改进信息熵和LSTM网络的轴承故障诊断

何群, 余志红, 陈志刚, 王衍学, 幸贞雄

(1.北京建筑大学机电与车辆工程学院, 北京 100044; 2.中国劳动关系学院安全工程学院, 北京 100048; 3.贵州省劳动保护科学技术研究院, 贵州 563000)

滚动轴承在机械运作的过程中由于其在载荷作用下需要承受负载和减小机构间的摩擦,故轴承的内圈、外圈及滚动体很容易出现故障,进而威胁到机械设备和操作人员的安全。因此,研究准确有效的故障诊断方法,对减少事故的发生具有重要意义[1]。

通常情况下,对于滚动轴承进行机械故障诊断的关键步骤包括特征提取和模式识别。在当今数据爆炸的时代,传统的时域和频域的分析方法虽然应用广泛,但是由于采集到的信号经常会受到多个振源的扰动、耦合,再加上环境存在噪声,以至于得到线性和平稳性较差的信号[2]。基于上述原因,传统的轴承故障诊断方法已经越来越不能满足诊断要求[3]。

随着计算机硬件技术的发展,诊断方法也飞速进步。文献[4]提出的经验模态分解(empirical mode decomposition,EMD)虽然能用自适应基函数处理线性和平稳性较差的信号,得到具有较高信噪比的结果[5],但是在现实中轴承信号往往是非线性非平稳的。而且该方法会出现模态混叠,导致信号分解之后的精度出现问题。而集合经验模态分解(ensemble empirical mode decomposition,EEMD)对模态混叠的问题能实现有效抑制[6]。变模态分解(variational mode decomposition,VMD)作为一种新型自适应信号处理方法[7],将信号分解过程转变为求解变分问题的过程,通过搜寻变分模型的最优解来实现信号的自适应分离,能对非递归、变分模态分解的模式对信号进行分解,克服了模态混叠和端点效应[8]。单纯的信号处理并不能对故障进行自适应诊断,因此越来越多的学者开始研究自适应的故障分类方法。Kiranyaz等[9]总结了一维卷积神经网络(one-dimensional convolutional neural network, 1D-CNN)可以直接应用于原始信号,而不需要任何预处理或后处理,如特征提取、选择、降维、去噪等。Zhou等[10]提出了一种基于长短时记忆网络(long short-term memory networks,LSTM)与迁移学习(transfer learning,TL)相结合的方法,对滚动轴承的4种不同工作状态进行分类识别。但是时域、频域信号的数据过长,即使经过特征提取之后输入LSTM神经网络中进行训练的数据量依旧十分庞大,导致网络的收敛性差,训练时间长。由于信息熵(information entropy)主要依赖于概率分布,有效地反应数据所带的信息量,因此选择以信息熵为特征[11]。

对于滚动轴承故障出现时的振动信号,由于其不稳定、非线性,单纯的EEMD和VMD难以实现特征提取和故障分类;1D-CNN直接从原始时域信号学习的时间成本太高;LSTM存在处理长数据存在天然劣势。因此,在前人研究基础上提出一种基于改进信息熵的LSTM网络作为滚动轴承故障信号分类的模型,通过用EEMD和VMD分别求取原始信号的本征模式函数(intrinsic mode function,IMF),通过改进信息熵(improved information entropy,IIE)构建特征向量,将特征向量输入LSTM网络中得到训练后的网络模型,用于分类诊断,得出实验结果。结果表明,所提出的方法能够对多种轴承故障进行分类,并与传统方法相比有较高准确度。

1 改进信息熵和LSTM网络

1.1 改进信息熵理论

信息熵是衡量系统有序化程度的一个度量,可以理解成某种特定信息离散随机事件出现的概率。系统越有序,熵值越低;反之系统越混乱,熵值越高。信息熵具体求解方式如下。

对于任意变量X,信息熵H(X)的表达式为

(1)

式(1)中:pi为第i个IMF分量的能量占总能量的比值,IMF分量由EEMD和VMD得到。

pi的计算公式为

(2)

(3)

式(3)中:x(t)为输入关于时间t的信号序列;xi为第i个信号。

如果将信息熵用于描述轴承运动,在轴承出现故障时,轴承运动就会出现周期性的冲击,它的表现就会更有序。因此,通过对原始信息分析后得出的IMF如果含有轴承的故障信号,则它的脉冲就会更秩序,也就会使得它的信息熵的值更小。但是,在轴承早期故障时,故障特征不够明显,从而导致识别率较低。为避免信息熵在一些特征不明显的故障分量中存在被识别率低的问题,需要对信息熵进行改进,较明显方法是将各个IMF特征放大。而峭度指标则通常作为描述波形峰态的重要参考,是评估故障冲击式的重要指标。要使模型对冲击信息较灵敏可以通过峭度对信息熵值加以改进,定义为

(4)

式(4)中:Qi为第i个IMF分量的改进信息熵;Hi和Ki分别为第i个IMF分量的信息熵和峭度指标。

因为信息熵只表示对应的IMF信息量,而由于环境噪声等原因故障信息在熵值上表现不明显,由于每一段特定信号分解出来的IMF数量一定,因此IMF的改进信息熵会有一个上限值为

(5)

式(5)中:n为分解得到的IMF数量;Q为信息熵。

单一组原始信号的平均改进信息熵为

(6)

1.2 LSTM单元

LSTM是对传统神经网络的改进[12],对于循环神经网络存在的两个问题:梯度爆炸和消失,该方法能进行有效处理。LSTM单元结构如图1所示。

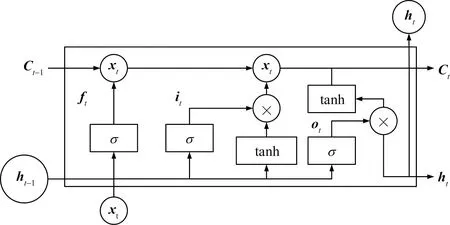
Ct、Ct-1分别为t时刻和t-1时刻存储单元信息;it为输入门;ft为遗忘门;ot为输出门;xt为t时刻输入向量;σ为sigmoid函数;ht、ht-1分别为t时刻和t-1时刻隐藏层输出信息;tanh为激活函数

LSTM由门限和记忆细胞构成。通过图1可知:当输入数据为xt时,LSTM单元的记忆细胞输出分别为

(7)

式(7)中:Whf、Whi、Who分别为遗忘门、输入门、输出门与上一隐藏层之间的权重矩阵;Wxf、Wxi、Wxo分别为遗忘门、输入门、输出门之间的循环权重矩阵;bi、bo、bc、bf为偏置向量;σ为sigmoid函数。

1.3 EEMD算法

EEMD是基于EMD改进而来,在原有信号基础之上加入白噪声,将信号筛分成若干仅含单一变量的IMF[13],利用白噪声频谱均匀分布的特点有效解决了EMD分解得到的IMF信息模糊的问题[14]。EEMD算法分解目标振动信号的步骤如下。

步骤1确定EEMD的运算次数r和高斯白噪声的标准差δ。

步骤2在原始数据x(t)的基础上,加入白噪声hi(t),得到新的信号xi(t),其中i为分解次数,i=1,2,…,r。

xi(t)=x(t)+hi(t)

(8)

步骤3对新构成的信号xi(t)进行EEMD分解,得到IMF分量cij(t),其中cij(t)为第i次分解后得到的第j个IMF分量。

步骤4重复步骤2和步骤3r次,得到r组IMF分量构成的序列{cij(t)}和r组余量{Resij}。

1.4 VMD算法

VMD能通过设定分解层数K,将复杂信号进行分解成若干个IMF,以此在不受人工干预的情况下得到K个有限带宽的分量。

VMD算法可表示为[15]

(9)

(10)

式中:uk={u1,u2,…,uk}为各个IMF分量;ωk={ω1,ω2,…,ωk}为每个分量中心的频率;X(t)为初始输入信号,∂t为对t求偏导;δ(t)为冲击函数。

最优解通过二次惩罚因子α,拉格朗日数乘法的乘子λ(t),构造增广拉格朗日函数而得到。

VMD的分解步骤如下。

步骤2利用迭代更新参数uk和ωk。

步骤3更新拉格朗日乘子λ,其中ω为中心频率。

步骤4设置判断精度e>0,如果和停止条件不相符,则返回步骤2,反之则停止迭代,式(12)为判断条件。

(11)

(12)

通过上述步骤进行VMD分解后得到IMF,取包含大部分有效信息的5个分量作为研究对象。

综上所述,方法结构框架如图2所示,通过对原始数据进行EEMD和VMD分解处理,得到一系列的IMF分量;求IMF的改进信息熵,组合成特征向量,分成训练集和测试集,训练LSTM网络。

图2 基于改进信息熵LSTM的诊断流程图Fig.2 Diagnostic flowchart based on improved information entropy LSTM

2 滚动轴承故障诊断实验及分析

2.1 实验数据来源

为验证本文设计故障诊断方法的可行性,将使用该方法对西储大学的轴承数据中心种子故障测试数据进行分析。该数据包含多种不同故障类型和不同故障程度的轴承工作状况。数据采集自驱动端,选取4种轴承工况下的正常工作数据,105组12 000的故障数据包含故障直径各不相同的内圈故障、滚动体故障、加载于06:00方向的外圈故障,故障点由电火花技术进行精确加工。数据的采样频率为12 kHz。轴承故障的严重性用故障尺寸的大小来模拟,不同的转速对应的是模拟不同的负载。

为减少噪声干扰,将轴承原始数据信号进行归一化处理,在[0,1]这个区间内最终得到各个工况的样本数据。

2.2 实验结果分析

首先对输入的一组原始信号做EEMD,设定分解的集合数NE=50;噪声标准差与输入信号标准差之比Nstd=0.01。画出EEMD分解得到的前5个包含主要信息的IMF如图3所示。

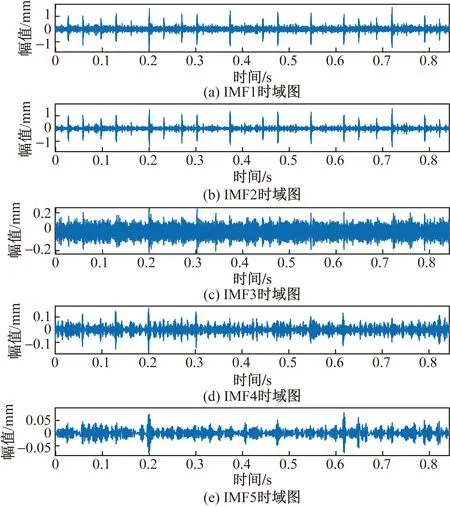
图3 EEMD分解图Fig.3 Exploded view of EEMD

同时,对输入的信号进行VMD分解,设定约束数据保真度的平衡参数α′=525;双重上升的时间步长τ=0,表示噪声松弛;要恢复的模式数K=4;选取init=1,表示所有的ω开始时都是均匀分布的(ω为预计模态的中心频率);收敛准则的公差tol=1×10-7。VMD分解得到的图像如图4所示。

图4 VMD分解图Fig.4 Exploded view of VMD

然后,对生成的各个IMF求取其改进信息熵。改进信息熵的求取是将输入的各个IMF按照时间序列,通过寻找各个IMF信号的各个分段的能量谱中能量最大的点,以分段数和最大能量差值的绝对值为约束求取分段间隔,再以出现概率不为零的每一段和得到各个IMF的信息熵Hi,再将Hi和对应的IMF峭度相乘得到改进信息熵Qi。通过EEMD和VMD得到的分量求得改进信息熵Hi后,以改进信息熵为信号特征得到对应特征向量并划分训练集和测试集。设置每种故障形式样本数n=1 500,LSTM网络为两层,每层网络包含的单元数为64;激活门函数为S型sigmoid函数,从S型函数的特性及结果满意度考虑初始权值为(-1,1)中的任何数;全连接层两层,每层包含的神经元个数也为64;后接Softmax分类器,作为输出层。结构如图5所示。

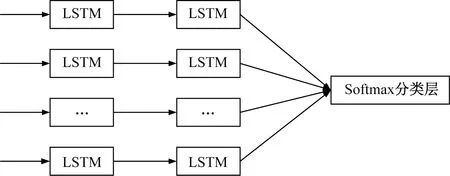
图5 LSTM网络结构Fig.5 LSTM network structure

轴承的内圈故障、滚动体故障、外圈故障和正常轴承数据分别为标签1,2,3,4。获得标签数据集之后,划分成70%训练集、20%验证集与10%测试集。分出测试集是为了客观地判断训练所得参数对新数据的符合程度,交叉验证的思想用于对模型参数测试,可避免模型被过度训练。当验证集的性能开始下降时,训练结束。LSTM的学习效率设置为0.001,训练集设置每轮迭代次数为30次,迭代轮数为100轮,最大迭代次数在2 400～3 000次进行微调;验证集设置每轮迭代频数为50次,最大迭代100轮,将验证容忍度设置为验证集的损失不再降低时停止训练。训练过程的准确度和损失函数图像如图6和图7所示。

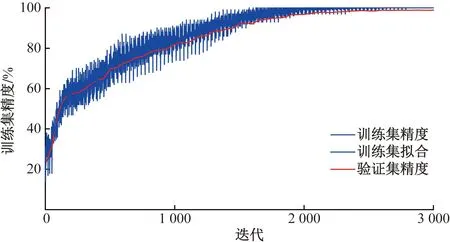
蓝色实线为经过平滑处理的训练数据;黑色点划线为 验证集的准确度

橙色实线为平滑处理后的损失函数;黑色点划线为验证集的损失函数

从图6、图7可以看出,验证集在进行约2 700次迭代之后函数图像收敛。此时损失函数达到平稳值,不再继续降低,验证集精度最终为98.73%。

为了证明本文方法可行且稳定,进行多次实验得到了该方法测试数据平均诊断正确率,结果如表1所示。

表1 多次实验准确率Table 1 Accuracy of multiple experiments

10次验证集精度测试数据的平均准确率为98.705%,标准差为0.002 1。为证明本文方法相较于其他经典方法的优越性,选用VMD-LSTM、EEMD-LSTM、人工神经网络(artificial neural network,ANN)、支持向量机(support vector machine,SVM)进行比较分析。VMD-LSTM用每个输入数据VMD分解得到的分量构成数据集进行训练,VMD分解的相关参数与本文方法设置一致,LSTM的学习率为0.001,两层LSTM,两层全连接层,采用sigmoid激活函数,迭代次数为2 000次;EEMD-LSTM采用EEMD求取每个输入原始数据的IMF后组成相应数据集进行训练,同样采取两层LSTM及sigmoid激活函数,学习率设置为0.001,迭代次数设置为3 000次;ANN的结构参数由反复调试确定,结构为24-50-7,学习率为0.1,迭代次数为400;SVM采RBF用核函数,结构参数由10折交叉验证法确定该核函数的惩罚因子为30,半径为0.31。不同方法的5次测试结果如图8所示。5种方法的平均测试准确率如表2所示。

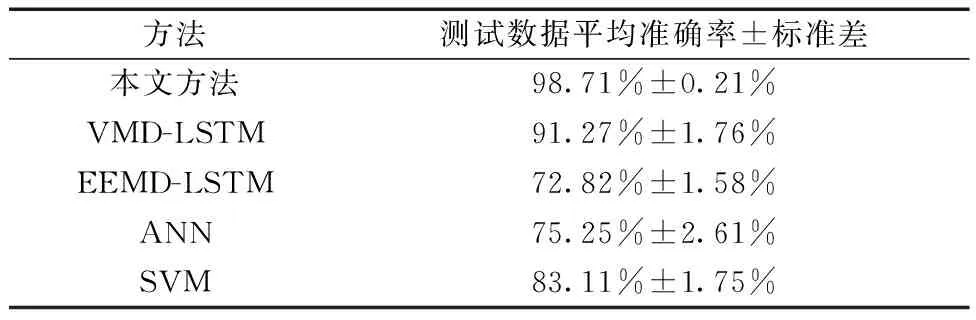
表2 不同方法的测试准确率Table 2 Accuracy of different methods

图8 多种方法多次实验准确率对比Fig.8 Comparison of multiple methods

3 结论

提出一种基于改进信息熵和LSTM的滚动轴承故障诊断方法,对轴承故障识别有较高的准确度,和其他经典方法相比,具有更大的优势。得出如下主要结论。

(1)对IMF的特性以及改进信息熵这一特征进行充分应用,将EEMD和VMD能对信号进行自适应分解的特性和改进信息熵结合,既避免了复杂的人工提取特征的过程,又能大量减少输入到网络中的数据量。

(2)提出了改进信息熵,通过和峭度指标的改进放大了包含故障的分量熵值,使得到的特征向量同时包含信息量大的分量和本来故障信息小的分量,既避免了丢失特征项,增强了鲁棒性LSTM网络的性能,在故障识别准确率上要优于一些经典模型。但对于复合故障分类精度会有所下降。今后将对该难点更深入地进行研究。