考虑综合经济性的风光配电网储能优化配置
闫群民, 李召, 马永翔, 张芮华, 张翔
(陕西理工大学电气工程学院, 汉中 723000)
发展可再生能源是缓解传统化石能源日渐枯竭的重要手段,也是中国实现“双碳”目标早日达成的重要方法[1-3]。近年来,以风光为代表的可再生能源凭借着其绿色、环保的优势而得到了快速发展[4]。但是风光出力具有随机性和波动性,对于配电网的频率和电压稳定带来了很大的挑战,同时也给配电网的经济可靠运行产生了干扰[5-7]。在配电网中接入储能设备可以有效解决这些问题,由蓄电池组成的储能系统(batter energy storage system,BESS)具有安装灵活、能量密度高、充放电速度快的特点,由于储能在配电网中的安装位置和配置容量关乎着配电网运行的稳定性和经济性[8-10],合理的位置和容量不仅可以有效平抑风光出力的波动性,同时又能改善系统电压质量、降低网损、提升经济性。因此,配电网中储能系统的优化配置具有广阔的应用前景和研究价值。
目前对于储能的优化配置问题,中外学者已开展了大量研究。文献[11]考虑了配电网的网损灵敏度,以有功网损和电压偏差最小为目标,建立了配电网储能优化配置模型。文献[12]提出了一种基于新能源出力保证率轨迹灵敏度分析的储能配置方法,建立概率潮流的轨迹灵敏度分析模型,提出了使得概率潮流不发生越限储能容量配置策略。文献[13]利用混合储能的不同特性来对微电网的功率波动问题进行了相关研究,确保含风光的微电网系统在进行并网时能够安全可靠运行。文献[14]在考虑了多场景的前提下借助上下限约束法进行储能配置,并且构建目标函数时考虑了配电网的运行成本,但上述模型未从储能投资经济性角度出发,可能会产生较大成本。目前储能电池的成本问题也影响着储能在电网中的应用,文献[15] 综合考虑了储能的售电效益、安装储能前后负荷聚合商的违约成本、购电成本和运行维护成本,以效益最大为目标建立了储能优化配置模型。文献[16]利用小波包分解算法对风电出力曲线进行处理,得到储能系统全年功率响应曲线。以储能年综合成本最低为目标,对风电场中的储能进行规划,文献[17]以购电成本、网损成本和投资成本之和最小为目标建立模型。然而上述模型没有同时兼顾配电网的稳定性。
在求解算法方面,文献[18-19]分别使用传统差分进化算法和多目标粒子群算法(multi-objective particle swarm optimization, MOPSO)进行储能选址定容优化。文献[20]先是按照电压稳定度为指标进行选址,然后将有功网损最小作为优化目标利用改进粒子群进行求解,但这些传统优化算法在求解储能选址定容优化问题时存在收敛速度慢、易于限于局部最优等问题。文献[21]将传统遗传算法与模拟退火算法相结合降低了系统的成本,但其在求解储能配置问题时遗传算法的交叉变异操作随机性较强。文献[22]使用原始多目标人工蜂鸟算法进行混合储能的配置优化,人工蜂鸟算法虽然作为近年来新发展出的优化算法具有很多优点,但在进行求解时具有易于陷入局部最优和有丢弃解的现象,需要进行改进。
针对以上情况,同时考虑储能配置的经济性和配电网稳定性指标,在储能年投资成本的基础上考虑基于分时电价的网损成本和年峰谷差收益,然后以成本和电压偏差为目标建立储能选址定容数学模型,利用改进多目标遗传二代算法(improved multi-objective nondominated sorting genetic II algorithm,INSGA-II)进行求解,最后采用改进理想点决策法(improved ideal point based decision,IIPBD)选取最优储能配置方案,在IEEE-33配电网模型里进行仿真,验证所提模型的合理性和优化算法的性能。
1 储能年投资成本分析
配电网侧电池储能系统在项目周期内的投资成本由初始电池本体购买成本、储能系统辅助设备成本、运行维护成本和回收价值构成[23-24],考虑时间价值因素对货币的影响,将全寿命周期成本进行年化。
(1)初始购买成本C1。
(1)
(2)
式中:μ为折现因子,将储能系统投资成本在使用寿命内进行年化,折算成年投资成本;r为折现率,取值为0.05;y为使用寿命;Na为蓄电池的安装数量;Pa为第a台蓄电池的额定功率;Ea为第a台蓄电池的额定容量;np和ne分别为蓄电池的单位功率价格和单位容量价格。
(2)辅助设备成本C2。包括能量管理系统和变流器等设备。
(3)
(3)年运行维护成本。电池储能系统的年运行维护成本C3主要由年固定运行维护成本Cfix和年可变运行维护成本Cvar构成,可表示为
C3=Cfix+Cvar
(4)
固定运行维护成本包括储能系统维护和日常管理,跟蓄电池的保持状态无关,与蓄电池的功率和种类有关,可表示为
Cfix=nfix,aPa
(5)
式(5)中:nfix,a为电池的单位功率年固定运行维护成本价格。
随着储能系统运行时间的增加,电池会出现一些损坏,可变运行维护成本主要与蓄电池运行时间和每天的充放电量有关,主要是电池运行费用,可表示为
(6)
式(6)中:nvar,a为电池的单位充放电量运行维护成本;λd为电池第d天的充放电量;D为蓄电池一年的工作天数。
(4)回收价值。当项目周期到期,电池可以回收产生一定的效益,可表示为
C4=krC1
(7)
式(7)中:C1为初始购买成本;kr为回收的系数,取0.1。
2 储能优化配置数学模型
目前中外储能电池主要有纳硫、铅酸、铁锂等。锂电池具有寿命长、能量密度高、充放电快等特点,近年来被广泛应用,因此在选择储能电池方面以锂电池作为储能器件,电池相关参数[25]如表1所示。

表1 电池参数设置Table 1 Battery parameter settings
2.1 蓄电池运行模型
蓄电池的剩余电量随着时间的变化与储能充放电功率保持着一定的关系,当蓄电池在充电状态下时如式(8)所示,当蓄电池在放电状态下时如式(9)所示。
开始充电时可表示为
(8)
开始放电时可表示为
(9)
式(9)中:E(t+1)为t+1时刻的剩余电量;E(t)为t时刻的剩余电量;Pch(t)为t时刻的充电功率;Pdis(t)为t时刻的放电功率;ηch和ηdis分别为充放电效率;Δt为充放电过程的时间间隔;α为电池自放电率。
2.2 目标函数
考虑在配电网系统中安装储能系统有减少电压偏差、降低有功网损等有利于改善配电网电能质量的作用,分析蓄电池的充放电过程,在考虑网损费用和储能系统主要收益的基础上,以年综合成本、电压偏差为目标,在满足配电网和储能稳定运行的约束条件下,建立储能系统优化配置数学模型。
(1)考虑峰谷差收益的储能年成本费用。基于目前峰谷电价相差很大,在配电网中安装储能系统可以利用“低储高放”的特性产生收益,更早的完成对项目周期成本的回收,其年收益表达式为
(10)

分时电价参考陕西省发改委发布的居民分时电价收费标准,具体电网分时电价如表2所示。则储能电池考虑峰谷差收益的年成本f1表示为

表2 电网分时电价Table 2 Time-of-use price of power grid
f1=C1+C2+C3-C4-Cin
(11)
(2)基于分时电价的网损改善目标。由于加入储能可以有效提高电网的输配电能力,从而降低网损成本,利用分时电价机制将网损折算成成本费用,网损改善目标f2可表示为
(12)
式(12)中:BL为线路总数;λt为t时段的分时电价;rij,t,d为第d天t时刻线路ij段的电阻;Ui,t,d为第d天t时刻节点i上的电压,Pij,t,d、Qij,t,d分别为第d天t时刻支路ij上流过的有功功率和无功功率。
(3)节点电压偏差。风光的不确定性会引起配电网的电压偏差,利用储能可以有效抑制电压的波动性,以日累计所有节点的电压偏差之和为目标,f3表达式为
(13)
式(13)中:N为总节点数;Vi,t,p和Vi,t,N分别为t时刻节点i的实际电压和额定电压。
提出3个目标函数,考虑峰谷差收益的年成本为f1;系统网损成本为f2;日累计电压偏差和为f3。由于f1、f2均为成本费用函数,因此可以将f1和f2合并作为第一个目标函数F1,代表经济性指标,f3作为第二个目标函数F2,代表配电网系统电压稳定性的技术性指标,储能多目标优化配置可表示为
(14)
2.3 约束条件
(1)系统潮流约束。
(15)
式(15)中:N为节点总数;PG,i为节点i的有功输出;QG,i为节点i的无功输出;PD,i为节点i的有功负荷;QD,i为节点i的无功负荷;Vi和Vj分别为节点i和j的电压;Gi,j和Bi,j分别为节点i和j之间的电导和电纳。
(2)节点电压约束。
Vmin (16) 式(16)中:Vmin和Vmax分别为节点i的最小电压和最大电压。 (3)支路电流约束。 Iij,min (17) 式(17)中:Iij,min和Iij,max分别为流过支路ij的上下限。 (4)储能充放电功率约束。 (18) 式(18)中:-Pa,max与Pa,max分别为储能系统充放电功率的下限与上限。 (5)储能荷电状态约束。 SOCmin≤SOC(t)≤SOCmax (19) 式(19)中:SOCmin、SOCmax分别为储能最小、最大荷电状态;SOC(t)为t时刻储能的荷电状态,设置SOC最小为0.1,最大为0.9。 (6)储能容量约束。 Ei,min≤Ei≤Ei,max (20) 式(20)中:Ei,min和Ei,max分别为节点安装储能容量的上下限,各个节点配置的储能容量满足上式约束,或者该节点配置储能容量为0。 (7)储能功率约束。 Pa,min≤Pa≤Pa,max (21) 式(21)中:Pa,min和Pa,max分别为节点配置储能功率的上下限。 (8)储能能量平衡约束。 (22) 式(22)中:Pc,d为储能设备第t时刻的充放电功率。 遗传算法因其适应于多种问题的求解而被广泛应用,所建立的是双目标的储能优化配置数学模型,相对于其他多目标算法,NSGA-II更适应于双目标的求解,但因算法本身机制还存在不足之处,在求解储能优化配置问题时由于其种群个体在进行交叉、变异时较为盲目,导致最优解容易陷入局部最优,并影响收敛速度,因此本文在NSGA-II的基础上进行改进,使用自适应交叉变异率,后期采用学习机制[26-27]。 3.1.1 标准NSGA-II 标准NSGA-II在进行选择时一般采取优胜劣汰的方法,选择适应度高的个体作为下一代,模仿自然界中染色体交叉时的过程,用于生成新的个体,这决定了算法的全局搜索能力[28]。标准的NSGA-II算法采用模拟二进制交叉算子,第k+1代个体的计算公式为 (23) 式(23)中:P1,k+1和P2,k+1为交叉后生成的第k+1代个体;P1,k和P2,k为被选中的第k代个体;βp和βq为均匀分布因子。 在进行变异时学习生物的基因变异,产生新的个体,第k+1带代个体计算公式为 (24) 3.1.2 改进措施 种群个体的交叉和变异是产生新个体的重要方式,然而,如果进行交叉和变异的方式盲目无序,可能会导致最优解的破坏,使得迭代结果容易陷入局部最优解。NSGA-II主要使用拥挤距离来评估种群的一个分散程度。本文旨在比较个体的拥挤距离和其所在Pareto前沿的个体平均拥挤距离,以确定交叉和变异概率的大小,从而实现种群的自适应进化[29],提高算法的全局搜索能力和收敛的准确性,交叉概率可表示为 (25) 式(25)中:h1为最小值交叉率;h2为最大值交叉率;k为迭代次数;kmax为最大迭代次数。 变异概率可表示为 (26) 式(26)中:v1、v2分别为最大和最小变异率。 为加强INSGA-II收敛速度,在后期引入学习机制。学习机制指的是子代通过学习前代的最优解染色体中的优良基因来提高子代个体的优秀率。后代从最优解中学习,并继承了最优解中的优秀信息,从而加快了算法求得全局最优解的速度。首先,在最优解染色体的长度范围内随机选择两个位置。然后,将这两个位置之间的基因段直接复制到子代对应的染色体位置上。然后使剩下的两边的基因片段分别重新排序赋值到子代的相应基因段位置,产生新的下一代染色体。 (1)归一化适应度值,可表示为 (27) (2)求理想点和非支配解之间的欧式距离平方。 (28) 式(28)中:ωs为第s个目标的权重系数 (3)比较所有Pareto解和目标欧式距离平方之和,然后按其最小距离来确定BESS的最优选址定容方案。 (29) 式(29)中:nt为Pareto解集中非支配解的个数。 基于改进后的NSGA-II算法对储能的接入位置和容量进行优化,图1为优化配置求解流程。 图1 储能优化配置求解流程Fig.1 Energy storage optimization allocation solution process 求解流程如下。 步骤1导入风电、光伏和负荷数据,进行算法的初始化。 步骤2载入IEEE-33配电网模型参数,使用matpower进行潮流计算,得出系统有功网损和电压偏差值。 步骤3染色体进行编码产生初始种群,计算个体的适应度值。 步骤4进行自适应变异,与全局最优解对比挑选出新的全局最优解,利用学习机制产生新的种群后代。 步骤5迭代完成后产生一组Pareto最优解,表示已经产生一组优化后的配置方案,利用(improved ideal point based decision,IIPBD)[30]法选出最优方案。 采用IEEE-33节点配电网模型为例进行储能的选址定容计算,系统拓扑结构如图2所示,系统的电压等级为10 kV,系统初始有功负荷为3 715 kW,无功负荷为2 300 kvar,储能可选择接入的节点为2-33。 图2 IEEE-33节点配电网结构图Fig.2 IEEE-33 node distribution network architecture diagram 选取西部地区风电场和光伏电站的出力特性作为输入功率,图3为典型日负荷曲线和典型日风光出力曲线。接入2个储能,在节点9、30安装200 kW风机,在节点14、20安装200 kW光伏。算法参数设置如表3所示。 图3 风光典型日出力曲线Fig.3 Typical daily output curve for wind and light 表3 仿真参数设置 为验证所建立模型及算法的有效性,选取3种不同的场景分别进行算例仿真分析,具体如下。 场景一不接储能 场景二接入风光和储能,采用标准NSGA-II算法进行求解。 场景三接入风光和储能,采用INSGA-II算法进行求解。 仿真结果如表4所示,可以看出,当在场景一中没有配置储能设备时,系统日累计电压偏差和偏大,场景二中当系统接入储能后减小了日累计电压偏差,在场景三中,当使用改进后的算法进行求解时,储能系统的综合成本和电压偏差得到了进一步的优化,其中成本减少了2%,电压偏差减少了3.5%,并且得到最佳储能安装位置和安装容量。 表4 不同场景优化结果Table 4 Optimization results for different scenarios 为进一步验证INSGA-Ⅱ的性能,表5列出了不同算法下的最优解。可以看出,用INSGA-Ⅱ求解出的两个目标的最小值是最低的。图4为使用不同算法获得的Pareto前沿,在INSGA-Ⅱ下得出的解集更加均匀,并且分布广泛,体现了算法的全局搜索能力。 图4 不同算法下的Pareto解集Fig.4 Pareto solution sets for different algorithms 表5 不同算法下最优解Table 5 Optimal solutions under different algorithms 优化后各部分费用如表6所示,可以看出,仅靠削峰填谷收益还不能够实现系统的成本回收,还需要靠调峰、政府补贴等来进行弥补。 表6 各部分成本费用Table 6 Costs of components 图5为系统未接入储能时和系统接入储能后使用改进前后的算法进行求解后的24 h节点电压三维曲线,可以看出,当系统未配备储能设备时,系统的电压波动较大,有的时刻甚至出现电压越限情况,当配置储能设备,采用初始NSGA-II进行求解时,系统节点电压分布如图5(b)所示,可以看出,当接入储能设备后,系统整体的电压水平得到了提升,均在规定电压范围之内。当配置储能设备,使用改进后的算法进行求解时,系统电压曲线如图5(c)所示,系统电压偏差更进一步得到了缩小,整体节点电压接近系统额定电压,有效地抑制了系统的电压偏差情况,同时也验证了对算法改进的有效性。 图5 电压曲线Fig.5 Voltage curves 优化后的储能24 h充放电功率和荷电状态曲线如图6所示。可以看出,两个储能设备的运行规律基本相同,均保持24 h全天运行,在00:00—08:00负荷低谷时储能进行充电,而在此时间段正是风力充足的时候,刚好增加了风电的消纳,而在14:00—17:00,光照充足,在此期间进行储能的充电也提高了光伏的利用率,SOC升高,在08:00—12:00和18:00—23:00,恰好是负荷的高峰期,此时系统中储能进行放电来缓解负荷加重对电网的影响。为了保证储能设备的长期稳定运行,设置其每天的SOC保持在0.1~0.9。 图6 储能充放电和SOC曲线Fig.6 Energy storage charge/discharge and SOC curves 在配电网中配置储能设备可以降低系统的峰谷差,有效的改善负荷曲线,利用在配电网中配置储能设备可以降低系统的峰谷差,有效的改善负荷曲线,利用其低储高放的特点来提高系统的整体经济性。 配置储能前后24 h内系统的负荷情况如图7所示。可以看出,在系统中没有接入储能设备时,负荷峰谷差为0.373 2 p.u.,在加入了储能设备后,系统负荷峰谷差变为0.247 8 p.u.,可以看出,储能的加入可以有效地起到削峰填谷的作用。 图7 配置储能前后负荷曲线Fig.7 Load curve before and after configuring energy storage 基于INSGA-II的储能选址定容问题,得出如下主要结论。 (1)在基于储能本身建设所需要的成本基础上,加以考虑网损成本和削峰填谷收益,以综合成本和电压偏差最低为目标,然后考虑系统约束和储能本身的约束条件建立储能选址定容数学模型。 (2)对NSGA-Ⅱ进行改进,采用自适应交叉变异法和学习机制来增强算法的寻优能力,设置不同场景在MATLAB上使用IEEE33节点系统进行仿真验证,得到最佳的储能安装位置及配置容量。 (3)将INSGA-II与MODE和MOPSO优化后的结果相对比进一步体现出了算法改进后的性能,从3种算法Pareto前沿中可以看出,INSGA-II具有更好的全局搜索能力。 (4)本文提出的配电网储能选址定容策略有效地降低了系统的电压偏差和综合成本,同时也验证了储能系统削峰填谷的作用。3 储能优化配置的求解
3.1 NSGA-II的改进
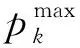
3.2 改进理想点决策法

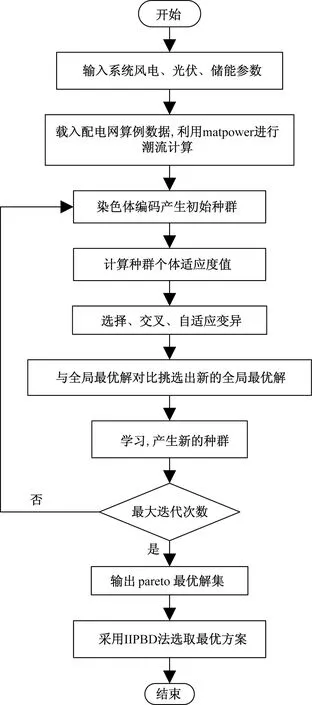
3.3 求解流程
4 算例分析
4.1 算例初始设置

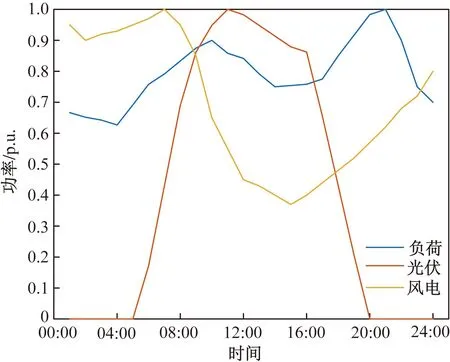

4.2 算例验证分析




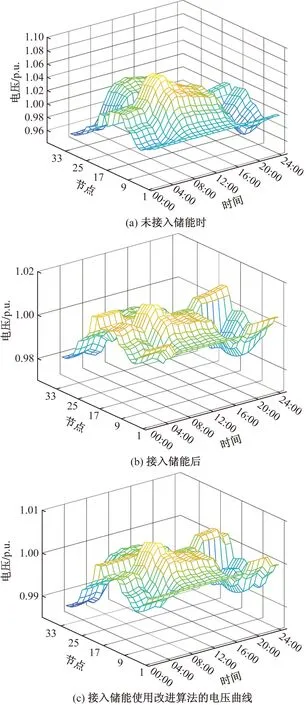
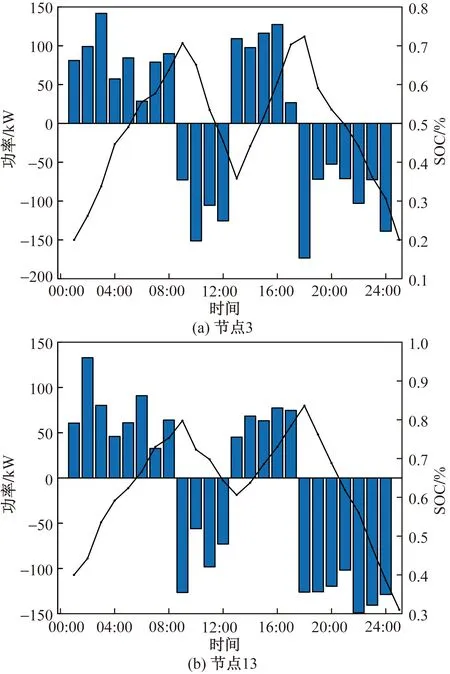
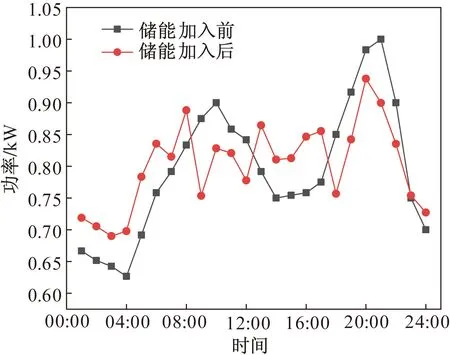
5 结论

