基于Cornell的自适应电离层闪烁强度的模型研究

易首成, 纪元法, 孙希延, 韦照川, 贾茜子

(桂林电子科技大学信息与通信学院, 桂林 541004)

电离层的电子密度分布不均匀体的百米尺度不均匀结构会造成全球导航卫星系统(global navigation satellite system, GNSS)信号的绕射、聚焦和散射,形成电离层闪烁[1-3]。根据电离层闪烁对信号的不同影响,可将电离层闪烁可分为幅度闪烁和相位闪烁,在地面接收端,不同传播路径上的无线电波信号相互干渉,造成电波信号振幅的随机增强或削弱,称为幅度闪烁,不规则结构的折射效应或衍射效应,造成接收到的无线电波信号相位发生快速起伏,称为相位闪烁[4-5]。低纬地区以幅度闪烁为主,而极区以相位闪烁为主,幅度闪烁不一定伴随有相位闪烁发生,而相位闪烁必然对应有幅度闪烁[6],幅度和相位的闪烁,致使信号接收机的测量误差增大、频繁周跳,严重时还会出现频繁、持续的卫星信号失锁现象[7]。由于电离层闪烁效应具有突发性、偶发性和区域性等特点[8],并且受电离层闪烁影响的GNSS信号很难复现,因此,建立能够准确描述电离层闪烁特性的仿真模型尤为重要。

目前,能够近似描述电离层闪烁信号模型有基于多重相位屏技术提出全球电离层闪烁模型(global ionospheric scintillation model,GISM)[9],幅度和相位具有一定的相关性的概率密度统计模型AJ-Stanford模型[10],基于赤道地区的大量实测数据的统计特性提出Cornell模型[11],以及可模拟出对接收机环路有严重影响的Canonical模型[12],该电离层闪烁模型被广泛应用于接收机算法研究和性能的评估中。徐昌元[13]针对Cornell模型对闪烁频率限定不严格,提出基于Cornell模型三参数电离层闪烁信号仿真模型。安盼盼[14]基于Cornell模型提出了多频点电离层闪烁模型。卢丹等[15]基于Cornell模型提出输入参数为电子总含量(total electron content,TEC)和导航数据的电离层闪烁模型。但在使用Cornell模型结合卫星信号模拟器生成的闪烁信号与实际设计的输入参数存在误差,未考虑幅度和相位的更新速率对模拟的闪烁信号的影响。因此,使用Cornell模型生成不同数据更新周期和闪烁强度的电离层闪烁信号,并周期的估算闪烁信号幅度闪烁指数S4的大小。在相同的数据更新周期下,随着电离层闪烁的增强,估算的幅度闪烁指数S4与模型输入的指数S4误差越大;在同一闪烁条件下,数据更新周期越大,两者的误差越大,并随着电离层闪烁的增强而增强。

由于研究电离层闪烁,重要的是电离层闪烁仿真模型生成的闪烁信号能够描述实际的闪烁变化,针对上述问题,提出基于Cornell模型的自适应指数S4的电离层闪烁模型,称为AS4-Cornell模型;通过仿真以及使用全球定位系统(global positioning system,GPS)模拟器模拟基于Cornell模型和AS4-Cornell模型的电离层闪烁信号,使用GNSS信号接收机提取载噪比,估算两个模型的电离层幅度闪烁指数S4,通过数据分析,验证AS4-Cornell模型的正确性以及对电离层幅度闪烁指数S4的改善性能。改善后的模型有助于低纬地区电离层闪烁模型的研究和建立有一定的参考意义。

1 电离层闪烁模型仿真

1.1 Cornell模型原理

Cornell电离层闪烁模型生成的闪烁信号的数学模型为

(1)

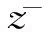
概率密度分布服从均值为零的高斯分布,闪烁引起的信号强度变化δI=δA2。Cornell模型生成电离层闪烁序列的实现框图如图1[8]所示。

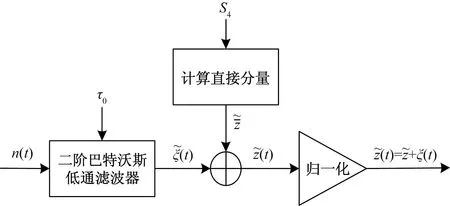
n(t)为复高斯噪声;τ0为去相关时间;为归一化前的时变分量 为归一化前的直接分量;为归一化前的闪烁序列; z(t)为归一化后的闪烁序列

1.2 AS4-Cornell模型原理

针对Cornell模型在同一闪烁条件下,数据更新周期越长,估计和模型输入的幅度闪烁指数S4的误差越大,并随着电离层闪烁的增强而增大的问题,提出AS4-Cornell模型。其实现框图如图2所示,在Cornell模型的基础上,增加复高斯白噪声权值分配和权值更新,三者构成一个闭环系统。

nr(t)为更新后的复高斯信号;MAX_ΔS4为最大S4偏差; zf(t)为闪烁信号;GW(n)为权值

1.2.1 BP神经网络PID原理

BP(back propagation)神经网络由信号的正向传播和误差的反向传播构成,即误差的反向传播算法[16]。采用的BP神经网络结构如图3所示,它分为输入层、隐含层和输出层[17-18]。输出层的神经节点有4个,其中,r(k)为期望幅度闪烁指数S4,y(k)为实际估算的幅度闪烁指数S4,e(k)为期望与实际的幅度闪烁指数S4的偏差;隐含层有5个神经节点,输出层有kp、ki和kd3个节点,wij(k)为输入层到隐含层的调节权值,wlj(k)为隐含层到输出层的调节权值。基于BP神经网络的PID控制结构如图4所示,采用的增量式PID调节控制系统的输出,整个系统的工作原理为,BP神经网络通过系统反馈的误差,自学习调节加权系数,输出最优的PID参数,最后通过PID参数的调节使系统达到最优的输出。

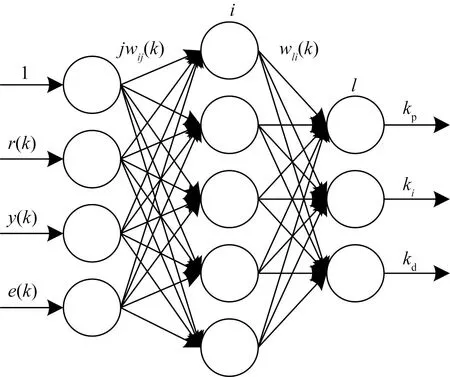
j为输入层节点;i为隐藏层节点;l为输出层节点;

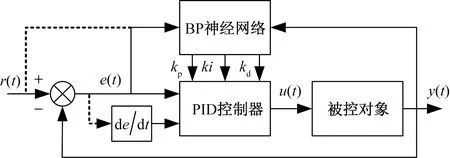
r(t)为输入;e(t)为误差;u(t)为被控参数;y(t)为输出

1.2.2 AS4-Cornell模型

通过Cornell模型和上述BP神经网络PID算法建立AS4-Cornell模型。首先根据幅度闪烁指数S4的估算周期对闪烁信号和复高斯白噪声进行分段;然后估算每段闪烁信号的幅度闪烁指数S4以及与模型输入幅度闪烁指数S4的偏差;最后采用BP神经网络PID算法根据偏差计算每段复高斯白噪声的权值,并对复高斯白噪声进行调整,使模型最终产生的闪烁信号满足闪烁指数S4的指标,具体如下。

根据幅度闪烁指数S4的估算周期把闪烁信号z(t)平均分成N段。

(2)

式(2)中:N为整数;zN(t)为周期分段后的闪烁信号;Ta为闪烁信号持续时间;T为估算周期。

估算每段闪烁信号zN(t)的幅度闪烁指数S4,S4与信号强度I的关系可表示为

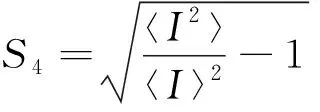
(3)

式(3)中:〈·〉为均值运算。

计算估算指数S4N与模型输入的指数S4偏差eN,当所有的偏差eN低于最大允许偏差MAX_ΔS4,输出最终的闪烁信号zf(t),否则以估算指数S4N模型输入指数S4以及两者误差eN作为BP神经网络PID算法输入层的参数,迭代求出适合系统的最优的PID参数kpN、kiN和kdN,然后由增量式PID原理更新权值GWN(n),可表示为

GWN(n)=GWN(n-1)+kpN[eN(n)-eN(n-1)]+kiNeN(n)+kdN[eN(n)-2eN(n-1)+eN(n-2)]

(4)

式(4)中:GWN(0)=1。

更新复高斯白噪声nr(t),并作为Cornell模型的输入,重新生成闪烁信号,它与分段后复高斯白噪声n(t)={n1(t),n2(t),…,nN(t)}和更新后的权值GWN(n)关系为

nr(t)=n(t)GWN(n) ={n1(t)GW1(n),n2(t)GW2(n),…,nN(t)GWN(n)}

(5)

2 模型仿真分析

仿真闪烁信号的配置参数:去相关时间τ0为1,仿真时间Ta为300 s,发生弱闪烁时S4取0.3,发生中等闪烁时S4取0.6,发生强闪烁时S4取0.8。通过分析Cornell模型和AS4-Cornell模型的时域特性和频率特性,以确保建立的Cornell仿真模型和AS4-Cornell仿真模型的正确性,同时在不同数据更新周期下,估算幅度闪烁指数S4。

2.1 时域特性分析

Cornell模型和AS4-Cornell模型的时域特性分析主要包括闪烁信号的幅度和相位的概率密度分布,图5(a)和图5(b)分别给出电离层发生弱闪烁、中闪烁和强闪烁时,Cornell模型幅度和相位概率密度分布仿真结果,图5(c)和图5(d)分别给出了AS4-Cornell模型的幅度和相位概率密度分布仿真结果。

图5 时域特性仿真结果Fig.5 Simulation results of time domain characteristics

从图5(a)和图5(c)可以看出,Cornell模型和AS4-Cornell模型在不同的闪烁程度下的幅度闪烁序列概率密度分布服从莱斯分布;从图5(b)和图5(c)可以看出,相位闪烁序列概率密度分布服从均值为0的高斯分布,仿真的闪烁信号的幅度和相位的闪烁序列概率密度分布与理论相符,并且当去相关时间保持不变时,随着电离层闪烁强度的增强,幅度和相位的概率密度分布图的中心点密度逐渐减小。

2.2 频域特性分析

Cornell模型和AS4-Cornell模型的频域特性主要从闪烁信号的幅度和相位的频谱分布展开分析,并使用最小二乘法线性拟合频率在0.7～3 Hz的幅度谱和0.8～10 Hz相位谱,其中p为最小二乘法拟合的幂律指数[19]。图6和图7分别给出电离层发生弱闪烁、中闪烁和强闪烁时,Cornell模型的幅度和相位的频谱分布的仿真结果。图8和图9分别给出AS4-Cornell模型的幅度和相位的频谱分布的仿真结果。

图6 Cornell模型幅度频谱Fig.6 Cornell model amplitude spectrum

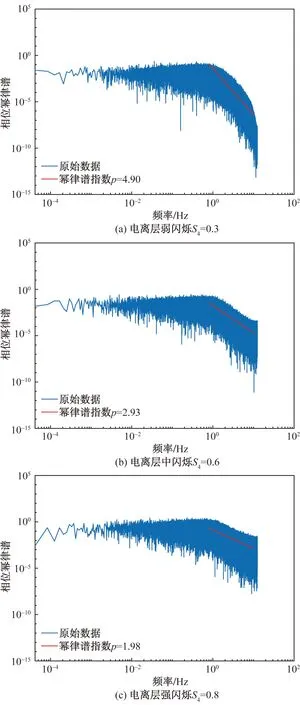
图7 Cornell模型相位频谱Fig.7 Cornell model phase spectrum

图8 AS4-Cornell模型幅度频谱Fig.8 AS4-Cornell model amplitude and spectrum

图9 AS4-Cornell模型相位频谱Fig.9 AS4-Cornell model phase spectrum

从图6～图9中可以看出,Cornell模型和AS4-Cornell模型在不同的闪烁程度下的幅度和相位的频谱均服从一定的幂律分布。因此,闪烁信号的幅度和相位的频域特性也与理论相符。

2.3 估算幅度闪烁指数S4

在不同电离层闪烁强度和数据更新周期为1、10、100 ms的实验条件下,仿真生成1 h的基于Cornell模型的电离层闪烁信号,然后每分钟估算一次幅度闪烁指数S4,结果如图10所示。

图10 Cornell闪烁信号的幅度闪烁指数S4估算结果Fig.10 Estimation results of amplitude flicker index S4 of Cornell flicker signal

从图10中可以看出,数据更新周期为1 ms时,估算的幅度闪烁指数S4与模型输入的指数S4在不同闪烁条件下的最大误差分别为0.003 2、0.015 4和0.029 7;数据更新周期为10 ms时,在不同闪烁条件下的最大误差分别为0.013 2、0.028 1、0.055 6;数据更新周期为100 ms时,在不同闪烁条件下的最大误差分别为0.056 3、0.153 8、0.174 3;在同一闪烁条件下,数据更新周期越大,两者的误差越大,并随着电离层闪烁的增强而增强;后续模型在GPS模拟器的应用中,这种波动更加明显,极大影响了实际情况下的电离层闪烁信号的模拟。

分析可知,当数据更新周期为100 ms时,估算幅度闪烁指数S4与模型输入幅度闪烁指数S4偏差最大,因此测试AS4-Cornell的改善性能和有效性,只需要在不同电离层闪烁强度、数据更新周期为100 ms和最大允许偏差MAX_ΔS4为0.001的条件下,仿真生成1 h的电离层闪烁信号,每分钟估算一次幅度闪烁指数S4,AS4-Cornell闪烁信号的结果如图11所示。

图11 AS4-Cornell闪烁信号的幅度闪烁指数S4估算结果Fig.11 Results of amplitude scintillation index S4 estimation of AS4-Cornell scintillation signal

图11所示的估算幅度闪烁指数S4的结果表明,在不同的电离层闪烁强度下, AS4-Cornell模型产生的电离层闪烁信号能够很好地反映模型输入的电离层闪烁指数S4的强度,并且与模型输入幅度闪烁指数S4的误差在设置的最大允许偏差0.001之内,相对于Cornell模型有了极大的改进。

3 基于GPS信号模拟器的电离层闪烁模型验证

3.1 模拟器原理

当电离层发生闪烁时,将会对GNSS信号的幅度造成乘性衰减干扰,对相位造成加性偏移干扰。因此在干扰下,GNSS接收机接收到的单颗GPS卫星信号数学模型为

r(t)=A0δAcos[2π(fIF+fd)t+φ0+ δφ]c(t)d(t)+n(t)

(6)

式(6)中:c(t)为扩频码;d(t)为导航电文;fIF为中频频率;fd为射频频率;δA为电离层闪烁引起的幅度衰减指数;δφ为电离层闪烁引起的相位偏移误差。

使用电离层闪烁模型产生成电离层闪烁信号,提取闪烁信号中的幅度和相位序列,并应用与模拟器的数字中频信号生成单元,电离层闪烁信号硬件实现框图如图12所示。

图12 电离层闪烁信号硬件实现框图Fig.12 Block diagram of hardware implementation of ionospheric scintillation signal

3.2 结果与分析

为验证AS4-Cornell模型对幅度闪烁指数S4的改进性能,模拟的闪烁信号配置为闪烁卫星号2,持续时间为15 min,闪烁序列更新周期为100 ms,去相关时间为1,载噪比为50 Hz,幅度闪烁指数S4分别为0.3、0.6、0.8;首先使用GPS模拟器分别模拟基于Cornell模型和AS4-Cornell模型的电离层闪烁的GPS信号,然后分析不同电离层闪烁强度下的GPS信号的星座图[20],结果如图13～图15所示。

I为同相信号;Q为正交信号

从图13中可以看出,电离层发生弱闪烁时,信号的幅度和相位扰动小,星座图呈环形分布;电离层发生中闪烁和强闪烁时,信号的幅度和相位扰动增大,星座图呈散点云状,随着闪烁强度的增强,幅度和相位的扰动剧烈,导致接收机的鉴相器工作点偏离0附近,I支路的幅度值出现180度跳变和波动值接近于0的情况增多,信号发生深度衰落。

载噪比变化如图14所示。可以看出,随着电离层闪烁的增强,载噪比的波动范围变大。当发生电离层闪烁时,载噪比为50 Hz,当发生电离层弱闪烁时,载噪比有3～6 Hz的波动;当发生电离层中闪烁时,载噪比有6 ～22 Hz的波动;当发生电离层强闪烁时,载噪比有7 ～26 Hz的波动。

CNO为载噪比;N为历元

每分钟估算的S4指数如图15所示。可以看出,1 min和17 min为未模拟电离层闪烁阶段,电离层幅度闪烁指数S4为0,在2～16 min分别模拟电离层发生弱闪烁、中闪烁以及强闪烁,两种模型的幅度闪烁指数S4的估算结果在预设值附近,但基于AS4-Cornell模型模拟生成的闪烁信号的电离层幅度闪烁指数S4与模拟器预设值的最大偏差为0.09,从而验证了改进模型的有效性。考虑到闪烁信号的幅度闪烁序列和相位闪烁序列是基于仿真的闭环条件下生成的,而不是基于实际硬件环境生成,因此指数S4的偏差未达到最大允许偏差的要求。

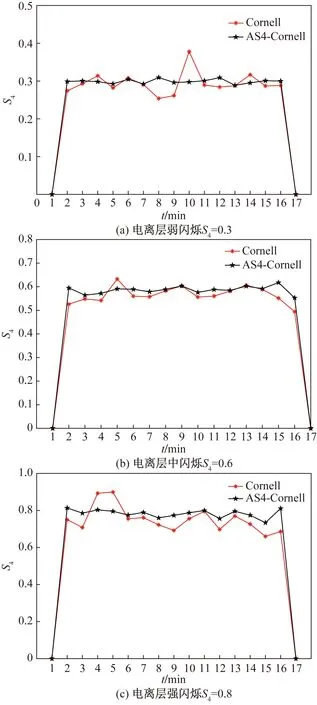
图15 PRN2 S4指数估算结果Fig.15 Estimated results of PRN2 S4 index

4 结论

为了改善传统的Cornell电离层闪烁模型的幅度闪烁指数S4与模型输入S4在周期估算时存在偏差的问题,提出AS4-Cornell电离层闪烁模型,并通过仿真和实际闪烁信号的模拟得出以下结论。

(1)仿真结果表明,AS4-Cornell模型生成的闪烁信号的幅度闪烁序列时域特性服从莱斯分布,相位闪烁序列时域特性服从均值为零的高斯分布;幅度和相位的频域特性符合幂律分布,与理论相符。估算的S4指数与模型输入的S4指数误差可以限定在设定的最大偏差内。

(2)对GPS模拟器模拟生成的闪烁信号进行S4指数的估算,结果表明,相比Cornell模型,基于AS4-Cornell模型生成的闪烁信号更符合设置的幅度闪烁强度。