基于深度强化学习的智能车辆行为决策研究
周恒恒, 高松, 王鹏伟, 崔凯晨, 张宇龙
(山东理工大学交通与车辆工程学院, 淄博 255000)
随着社会的发展,车辆保有量和驾驶人员数量持续上升,交通事故、环境污染、交通堵塞问题日益严重,智能化是引领汽车变革的技术之一,具有提高道路安全,减少燃油消耗,提高道路通畅性的巨大潜力,将改变人类的出行方式和社会结构。
传统的自动驾驶系统主要基于传感器信号结合人类驾驶的规则构造由环境到驾驶控制动作的模型系统,其优点是拥有较强的可解释性,但面对复杂多变的现实环境,模型的表达能力有限,自主学习能力和泛化能力[1-3]有限,鲁棒性难以保证。
DeepMind团队通过强化学习实现在雅达利游戏中控制智能体输出合适的离散的动作,后续的研究者针对连续动作问题,将David Sliver团队证明的确定性策略方法与DQN(deep Q-network)结合,提出DDPG(deep deterministic policy gradient)算法[4-6],该算法使得深度强化学习在解决连续空间问题上有了长足的发展。由于深度强化学习在各种场景中超越人类的表现,深度强化学习中环境和智能体的交互模式与自动驾驶中环境感知模块和决策控制模块的交互模式相似及深度强化学习表现出的优秀自主学习能力和面对不同场景的泛化能力,使得研究者开始通过深度强化学习解决自动驾驶行为决策的问题。
深度强化学习可以应用于自动驾驶的控制器优化、路径规划、超车换道、复杂导航策略的开发等策略中[7]。Huval等[8]基于卷积神经网络(convolutional neural networks,CNN)结构,在大量数据集基础上,通过深度学习和计算机视觉算法,完成了在高速公路环境下的车辆、车道实时检测任务。Bojarski等[9]提出了基于CNN网络结构搭建了自动驾驶端到端模型,分别在模拟器中和真实环境中进行了训练和测试,结果表明:CNN网络可以学习到有意义的道路特性及转向决策。Sallab等[10]将离散动作DQN算法和连续动作DDAC (deep deterministic actor critic algorithm) 算法应用于车道保持系统,证明了DDAC优于DQN。张永梅等[11]针对深度强化学习前期训练前期奖励随机性高难以获取问题,提出了内在好奇心驱的深度确定性策略梯度算法来完成机器人路径规划任务。结果表明:所提出的算法决策效果更优越,但实验中只测试了单一场景,模型在不同场景下的适应性无法得到验证。Cheng等[12]开发了CNN模型,通过标记的MSA(motion-sensitive area)数据集学习驾驶策略,在SUMO(simulation of urban mobility)中测试表明,基于强化学习的换道策略优于基于规则的换道策略。Zhao等[13]为了解决智能车辆受环境因素影响难以准确做出变道决策的问题,提出了一种基于贝叶斯优化的XGBoost(extreme gradient boosting)决策模型,实验结果表明:此模型决策识别准确率可达到95%以上,具有良好的决策效果,但该研究只选取前车和自车相关的数据作为模型的输入,忽略了环境信息对自车行为决策的影响。上述研究实现了端到端的行为决策,但训练过程需要大量人工标注数据且输出变量单一,模型适应能力有待提升。
鉴于此,利用深度强化学习的强拟合和交互特性针对动态场景中的超车行为,构建基于DDPG算法的端到端决策模型,结合场景及人类驾驶员操作习惯对输入端信息进行筛选,以筛选后的车辆状态、环境信息为输入,输出连续影响车辆行驶性能的多维度控制量,完成车辆端到端行为决策,省略了车辆系统的复杂建模过程。针对DDPG算法训练过程的奖励震荡现象引发的输出变量值突变问题,为进一步提升决策模型的控制精度和稳定性将控制变量作为输入对DDPG算法进行反馈优化,理论方面在强化学习中引入了反馈思想,实践方面提供了一种增加强化学习稳定性的方法。
1 深度强化学习DDPG算法
车辆自动驾驶过程可以看作车辆在复杂状态空间中的决策问题[14],深度强化学习作为深度学习和强化学习结合的产物,拥有深度学习优秀的感知理解能力和强化学习的决策能力,综上所述深度强化学习在自动驾驶领域拥有广阔的前景。
深度强化学习通常会把要解决的问题抽象成马尔科夫决策(Markov decision process, MDP)[15]过程,令{S,A,R,S′}为当前状态、动作、奖励和下一时刻状态的集合,设定t时刻状态st、动作at、奖励rt、t+1时刻的状态st+1作为一个元组{st,at,rt,st+1}进行收集便构成{S,A,R,S′}。智能体与环境依据策略π进行交互,收集多条包含回报的轨迹,如式(1)所示。
R=rt+1+γrt+2+γ2rt+3+…
(1)
式(1)中:γ为折扣因子。
求出所有轨迹的回报的平均值,通过优化策略π来最大化R,γ∈(0,1),代表未来的奖励对R影响逐渐减少。
Q函数Qπ=Er~π[Rt|st,at],其中,Er~π为奖励r在策略π下的期望,Rt为在状态s下选取动作at的奖励集合。强化学习的优化目标为寻得最优策略π*使得R的期望最大,即寻找使得式(2)成立的π*。
Qπ*=Er~π*[Rt|st,at]
(2)
式(2)中:Qπ*为状态st在最优策略π*下选取动作at的价值;Er~π*为奖励r在最优策略π*下的期望。
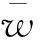
(3)
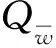
自DQN算法出现之后,一系列深度强化学习算法针对DQN所不能解决的问题应运而生,其中DDPG算法是针对DQN不能处理连续控制性问题提出的。其中,θQ′为目标网络Q′的权重,θu′为目标网络u′的权重,si、ai、ri分别为n条轨迹中的第i条轨迹的状态、动作和奖励,yi为计算的实际的Q值,θμJ为求出的策略梯度,n为采样的轨迹数量,a为Q对a求梯度,τ为更新幅度,使得网络权重缓慢更新,提高学习稳定性。

DDPG算法随机初始化Q网络Q(s,aθQ)和策略网络;μ(sθμ),其权重为θQ和θμ;初始化目标网络Q'和μ'并复制权重θQ'←θQ,θμ'←θμ;初始化经验回放池R;执行M个回合循环,对于每个回合初始化探索动作的随机过程,即噪声N;接收初始化状态s1;执行T个时间步长,对于时间t根据当前的策略和探索噪声选择动作at=μ(stθμ)+Nt;环境根据at反馈奖励rt和下一个状态st+1;存储轨迹(st,at,rt,st+1)到经验回放池R中;从经验回放池R中随机采样n条轨迹(si,ai,ri,si+1);计算实际的Q值yi=ri+γQ'[si+1,μ'(si+1θμ']θQ');通过最小化损失函数L来更新Q网络:L=1n∑i[yi-Q(si,aiθQ)]2;使用采样策略梯度来更新策略网络:θμJ≈1n∑iaQ(st,atθQ)st=si,at=μ(si)θμμ(stθμ)si软更新目标网络:θQ'←τθQ+(1-τ)θQ'θμ'←τθμ+(1-τ)θμ'结束T循环结束M
2 DDPG决策模型的建立
自动驾驶的研发路线[16]通常是在实车上进行数据测试和驾驶算法策略的设计与验证,然而实车测试研发成本高、调试周期长。随计算机技术发展,模拟仿真技术被广泛应用于自动驾驶算法开发,因此,研究者可通过自动驾驶仿真平台预先进行行为决策算法的测试和验证,其次再部署到实车中以提升研发效率。
2.1 智能体-环境交互模型
本文行为决策为单车和多车环境下利用状态信息直接控制车辆行驶动作(转向,油门,刹车),在车辆不驶出道路和不发生碰撞的前提下超越前方车辆。智能体-环境交互模型如图1所示,策略网络根据输入状态输出动作,Q网络根据输入状态和动作估计动作Q值,目标策略网络和目标Q网络保证未来奖励Qtarget计算更加稳定,奖励函数输出当前动作的奖励并作为计算Qtarget的真实奖励项,经验回放池负责存储轨迹{st,at,rt,st+1},TORCS仿真平台作为车辆运行交互环境。交互流程可以抽象为:①智能体接收环境给出的观测状态。在实际开发过程中,此状态实际是由智能体需求决定,而非环境直接给出;②智能体根据此状态通过策略网络做出相应的动作反馈给环境;③ 环境根据智能体做出的动作进行一次环境重置,同时给出新的观测状态以及对应的奖励; ④ 循环①~③的交互步骤。

图1 系统模型Fig.1 System model
2.2 状态信息和动作空间选取
为了获得更好的解释性和稳定性,采用传感器信息作为车辆与环境的交互数据。
针对高速公路环境,遵循人类驾驶员的能力、经验和驾驶习惯等[17-18]可设定保守驾驶员模型、普通驾驶员模型和激进驶员模型,普通驾驶员模型和激进驾驶员模型是同一类具有经验的驾驶员模型。行车过程中,驾驶员通常根据视觉和感觉来感知车辆及环境信息,感知信息的多少是上述三类驾驶员模型的不同之处。假设三类驾驶员反应时间相同,设定视觉参数V和感觉参数T(路况反馈和车辆振动等信息)保守驾驶员和经验丰富驾驶员的行为决策,如图2所示。
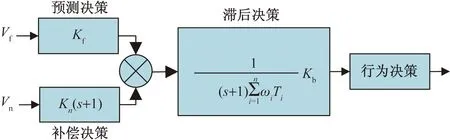
Vf为远处视野;Vn为近处视野;Kf为视觉预测参数,是视觉补 偿参数;ωi为i类驾驶员风格系数;Ti为i类驾驶员的感觉参数; Kb为感觉滞后参数;n为不同驾驶员感觉类信息的种类; s为复频率,是传递函数中的自变量
如图2所示,模型中的预测决策部分可作为比例系统,补偿和滞后决策部分可作为一阶系统。以通过弯道为例,对于缺乏经验的保守驾驶员,通常只考虑远处视野做出决策,不会借助近处视野对决策进行微调和对感觉信息不一定做出正确的判断,且决策不成熟,因此Kf参数较小,缺少补偿和滞后系统的微调;对于经验丰富的驾驶员,通常借助远处视野进行较好的决策,其次根据近处视野对决策进行微调,最后根据感觉信息对决策进行更加细微的调整,因此Kf参数较大,对于激进驾驶员Kn和Kb较大。综上所述,驾驶员收获信息的容量关乎决策的好坏。根据经验丰富的驾驶员模型,图2三系统需要考虑的传感器信息如表1所示。

表1 经验丰富的驾驶员感知信息Table 1 Perception information of experienced driver
智能驾驶车辆应在一个动态的、复杂的交通流中实施不同的行为,如车辆跟随、变道和超车。其中,超车策略由于交通的不确定性和复杂性发生碰撞可能性较大,因此完成超车策略具有挑战性。选取典型的超车场景如图3所示。

Δd为相邻车辆的纵向距离
结合表1和图3,根据策略需求,最终选取表2所列9类信息作为输入状态信息。
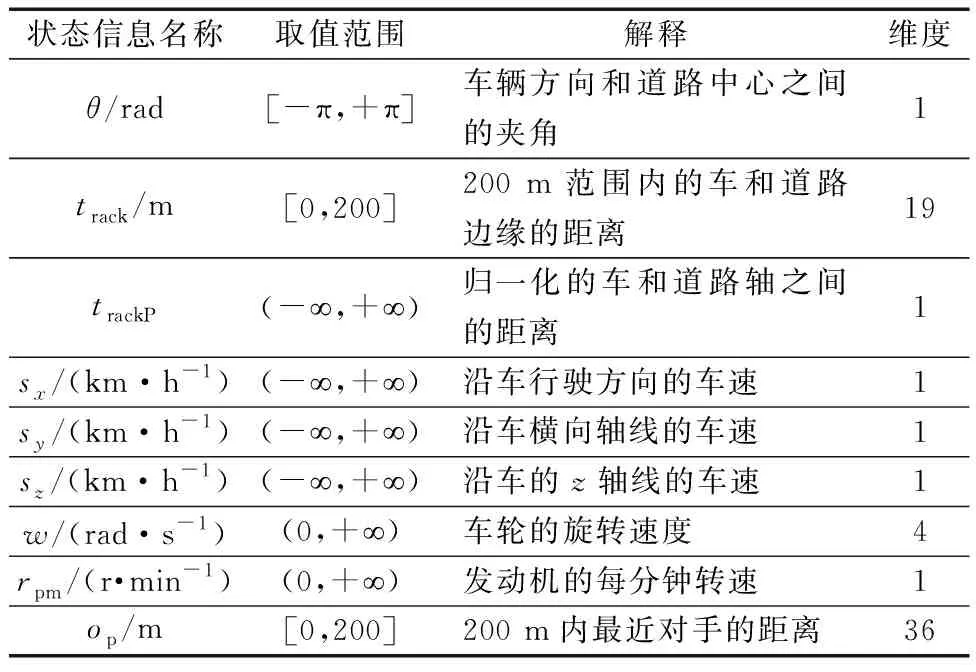
表2 状态信息Table 2 State information
基于DDPG算法可知,交互数据{st,at,rt,st+1}对策略网络和目标策略网络参数的更新具有重要影响,其中{st,rt,st+1}状态和奖励信息由环境提供。表3所示的归一化动作信息{at}由智能体提供,动作取值可在[0,1]内平滑连续的变化,与真实的驾驶控制动作相近,图4表征个别状态参数在道路环境中的位置。

表3 动作信息Table 3 Action information
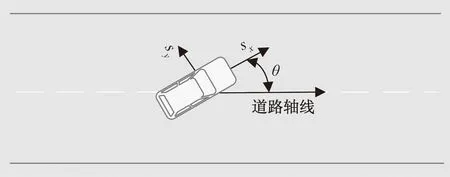
图4 驾驶过程关键参数Fig.4 Key parameters of driving process
3 奖励函数与DDPG算法超参数
为了使智能体更快地学到合理的策略,对于奖励函数rt的设计尤为重要。随着强化学习的发展,许多相关研究放弃了用传统的手工设计奖励函数的方式,采用逆强化学习来直接得到奖励函数,然而本文为了深入理解各个参数对行为决策的影响,依然采用传统的方式来设计奖励函数,奖励函数和DDPG算法的超参数选定直接影响算法的收敛速度和性能呢。
3.1 奖励函数设计
在深度强化学习中,奖励函数通过具体化和数值化任务策略与深度强化学习算法沟通,引导图5设计的神经网络探索状态空间中的决策相关因素构成状态-动作对。根据驾驶过程中的关键参数与状态信息对车道保持策略和超车策略分别进行了奖励函数的设计。
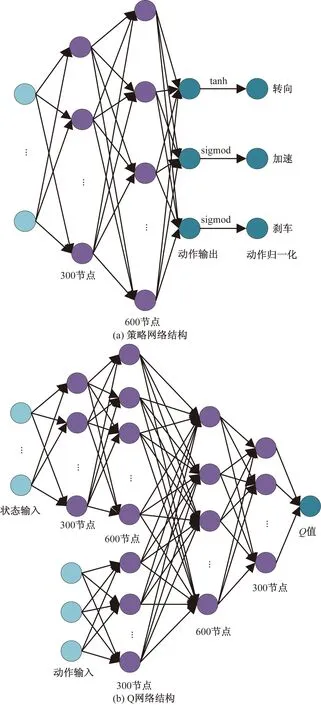
图5 网络结构Fig.5 Network architecture
针对车道保持策略,参考文献[19]提出的道路不满意度评价方法,提出以下3个约束。
(1)设定正向奖励sx(cosθ),使车辆以合理的速度沿道路中心前进,保证行车效率。
(2)设定惩罚项sy(sinθ),当车辆横向移动偏离道路中心时,给与负向奖励。
(3)高速状态下可能导致车辆漂移跑出道路,因此设定惩罚项sx(trackP),使车辆保持贴近道路中心。
根据上述约束,车道保持策略的奖励函数为
Rkeep=sx(cosθ)-sy(sinθ)-sx(trackP)
(4)
超车策略可以简化为车辆学习到合理的车道保持策略,与此同时学习超车策略。因此只需将车道保持的奖励函数添加超车项。超车策略的奖励函数为
(5)
式(5)中:Rover为仅考虑超越车辆数的奖励函数;Rtaking为超车行为总奖励函数;n′为车道中包括智能体在内的车辆个数;order为自车的位次。
为了防止神经网络模型陷入局部最小值,需要设计额外的奖励以及一个回合的终止条件,如表4所示。
3.2 DDPG超参数选定
在深度强化学习中,使用神经网络作为拟合状态-动作对的复杂非线性函数,根据表2所选的状态信息,设计图5所示的Q网络和策略网络。
在训练时对动作添加噪声,以更好的探索可能正确的行为,使训练的网络模型能够更好地迁移到不同的场景中。车辆行驶可以看作惯性系统,为了保护系统的安全性,采取OU(ornstein-uhlenbeck)噪声进行动作探索,如式(6)所示,OU噪声各参数的选择如表5所示。在动作探索的开始阶段,噪声较大,随着训练回合的增加,随着式(7)衰减至0,此外测试阶段取消噪声,避免噪声对测试结果的影响。DDPG算法的各超参数结合经验[20]和进行多次实验后给出,策略网络学习率la为0.000 1,Q网络学习率lr为0.001;下一步动作的奖励所占比重γ′为0.95,目标网络软更新参数τ为0.01;经验回放池(大小为100 000,抽样批次为32,训练回合为5 000,即M。

表5 动作探索的OU噪声系数Table 5 OU noise coefficient of action exploration
dxt=θm(μ-xt)dt+σdWt
(6)
式(6)中:xt为自变量;θm为反映变量均值回归快慢的参数;μ为均值;σ为回归过程的波动程度;Wt为维纳过程(布朗运动)。
(7)
式(7)中:noise为噪声量;i_ep为训练回合;explore为噪声递减程度,取10 000。
4 仿真与实验
4.1 仿真场景介绍
TORCS(the open racing car simulator)是一款开源的自动驾驶仿真平台,用户可以查阅使用不同的API来制定不同的行为决策,与驾驶环境进行交互。
TORCS中提供了不同种类的道路场景供研究者使用。在深度强化学习问题中,若训练过程中,选用简单的道路场景,在测试中容易出现欠拟合现象,选用复杂道路则容易出现过拟合现象。针对车道保持策略,为了使训练的网络适应不同路段,选择了包括左转弯、直线、反向转弯和急转弯4种常见路段的Aalborg道路,具体信息如图6(a)所示。设定策略完成距离为5 000 m,目标速度为120 km/h,在测试阶段,为进一步测试训练模型的普适性,选定的测试道路如图6(b)所示。

图6 车道保持策略训练和测试车道Fig.6 Lane keeping strategy training and testing lanes
为对高速行车工况超车策略进行针对性测试,选择图7所示的高速路车道。在该测试场景中当前方车辆行驶速度慢于自车速度时,自车为了寻求更高的驾驶速度和更广的驾驶空间,在符合安全要求的条件下实施超车行为。由于高速道路相对封闭,且路段类型一致,因此本文超车策略在同一道路进行训练和测试。
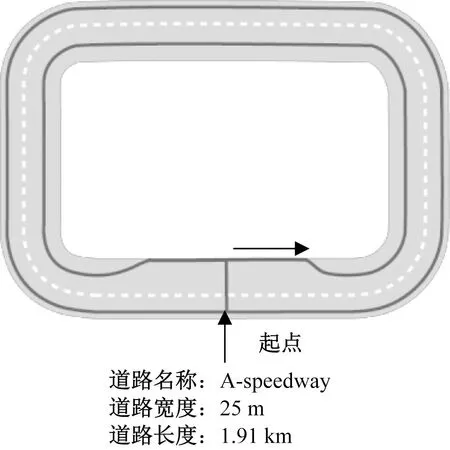
图7 超车策略训练和测试车道Fig.7 Overtaking strategy training and testing lane
4.2 仿真结果
4.2.1 车道保持策略仿真结果
在车道保持策略中,通过5 000回合的训练,如图8所示,平均奖励曲线趋于平稳,平稳时段内的奖励值和奖励函数相符,模型达到收敛。在图6所示的道路测试,测试表明自车可以根据实时环境信息顺利完成5 000 m的规定距离。

图8 车道保持训练奖励Fig.8 Training reward of lane keeping
由图9可知,以道路中心为基准,trackP∈[-1,1]表明车辆使用训练出的模型,在不同道路场景下依然可以较好地贴近道路中心行驶;当车辆偏移道路中心时,位置曲线波动幅度较大,说明自车能及时地根据实时环境信息调整动作以贴近道路中心行驶,表明模型具有较好的控制精度和适应性。

图9 横向误差Fig.9 Lateral error
测试阶段的车辆横向误差分布可以一定程度反映模型的适应能力,选取车道保持策略中的两次测试数据,横向误差分布如图10所示,可以看出,由于训练车道Aalborg弯道较多,故在测试中大横向误差(>0.5 或者 <-0.5)概率较高;在CG Speedway测试车道中存在较少的急转弯,大横向误差概率较小,表明训练的模型可以在合适的时刻进行刹车以降低车速通过弯道。两次仿真实验中,横向误差集中分布在0值附近;训练车道仿真中横向误差均值为-0.043 m,中位数为-0.049 m;测试车道仿真中横向误差均值为-0.048 m,中位数为-0.039 m,结合图9测试车道横向误差波动和训练赛道几乎同步,表明模型更熟悉训练环境,对环境有依赖性,测试环境下横向误差均值接近0,说明模型可以正确提取陌生环境中和策略相关的特征,可以完成既定策略;训练车道的横向误差中位数绝对值劣于测试车道,说明模型在较为复杂的车道环境中训练,没有出现过拟合现象,模型具有一定的可靠性。上述分析表明,自车在不同的道路环境中可以完成车道保持任务,验证结果总体表明:车辆能够根据传感器信息识别不同的道路环境,模型具有一定适应不同场景的能力。

图10 横向误差分布Fig.10 Lateral error distribution
4.2.2 超车策略仿真结果
在超车策略中,迭代训练6 000回合,如图11所示,奖励曲线相对平稳,可以完成既定策略,模型达到收敛,自车可以在无碰撞的前提下,超越前方速度慢于自身的车辆。如图12所示,将超车过程简化为准备超车、选择超车位置和超车完成。

图11 超车训练奖励Fig.11 Training reward of overtaking
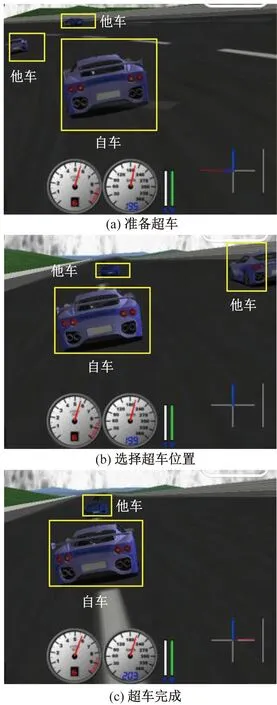
图12 超车子过程Fig.12 Overtaking sub-process
通过测试可知,测试过程中自车可根据实时干扰车辆信息,输出当前最优控制量,如图13所示。多次实验结果表明:实验过程中自车能够根据实时场景信息,在不发生碰撞的前提下完成超车;当前车留有足够空间时,自车会自动探索更大的行驶空间,更符合人类的驾驶员操作习惯。

图13 超车轨迹Fig.13 Overtaking track
4.2.3 改进模型效果分析
在车道保持策略中,从图14可以看出,DDPG平均奖励曲线虽然最终趋于平稳,然而会在某些时刻发生突变,表明车辆多次严重偏离道路中心,针对该问题,将自车上一时刻的控制变量反馈给算法输入端,如图14所示,对算法反馈优化后,平均奖励的突变次数会减少,说明所训练的模型控制精度有所提高,对于车辆的转向,刹车和油门的调节更加合理。
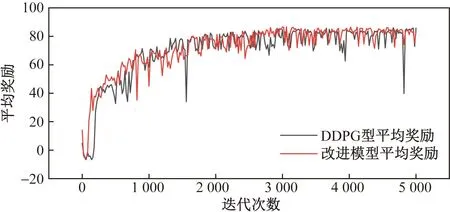
图14 奖励对比Fig.14 Reward comparison
图15和图16对两种训练的模型在测试车道中x、y分解速度进行分析,在测试中发现,改进模型可以完成车道保持策略,且完成距离远远大于DDPG模型,表明改进模型对新车道环境适应性优于DDPG模型。

图15 改进模型和DDPG模型测试结果Fig.15 Improved model and DDPG model testing results

图16 改进模型和DDPG模型的纵向速度箱线图Fig.16 Longitudinal velocity box line diagram of improved model and DDPG model
选取DDPG模型和改进模型的完成策略时间段基于统计学进行数据分析。从图15可以看出,DDPG模型与改进模型相比横向速度突变次数较多,纵向速度变化趋势不稳定,且DDPG模型忽略完成时刻横向速度最大为39.8 km/h,改进模型横向速度最大为22 km/h,说明改进的模型能更好地提取环境中和决策有关的特征信息。可以看出,纵向速度波动和横向速度波动同步,且集中在20 s和60 s处,此时大多位于弯道位置,符合驾驶习惯。表明改进模型的降速控制学习效果较优,所提出的方法能够根据实时道路信息输出合理控制量同时兼顾行车效率及行车安全。
此学习策略中目标车速为120 km/h,从表6和图16可以看出,改进模型测试中的速度平均值和中位数更接近于目标速度120 km/h且离散程度较小,说明改进的模型能更好地控制动作随时间连续变化。结合图15可以看出,改进模型可以更平滑的达到目标速度且发生的速度波动较小,测试结果总体表明改进模型能够使自车根据实时场景信息输出更为精确的动作,且能增加车辆的横向稳定性及行驶效率。
5 结论
针对传统决策过程中规则库建立繁琐,交互模型构建复杂问题,基于DDPG深度强化学习算法,提出一种端到端智能车辆行为决策方案,为使自车能够更清晰地关注周围车辆和环境的关键信息,结合驾驶员模型对自车状态信息、环境信息和周围车辆状态信息进行选取作为输入端,通过构建的模型直接输出控制量完成行为决策。为减弱由于模型适应不同环境时控制量突变问题使自车平稳地完成驾驶行为,利用相邻时刻控制量连续性对DDPG模型信息输入端进行优化形成输出对输出控制量的反馈。得出如下结论。
(1)DDPG模型能够根据实时环境信息输出合理的驾驶行为和控制量,与DDPG模型相比,改进的模型对车辆的转向,刹车和油门的调节更加合理;且车辆横向速度显著减小,最大横向速度减少39.24%,车辆舒适性以及车辆稳定性明显改善。
(2)基于深度强化学习的策略实现模型如何迁移到真实环境中一直是个难题,在未来的工作中,希望针对这一难题实现模型的迁移并在实车上进行实验。

