非均布压力作用下纯弯曲孔道预应力摩阻损失

杨雅勋, 刘寒, 柴文浩, 吴富勇, 叶家乐

(长安大学公路学院, 西安 710064)

预应力连续刚构桥是在役桥梁中较为常用的桥梁形式。但是随着预应力连续刚构桥运营时间的增长,其跨中会出现裂缝加剧、截面刚度削弱、挠度增大等问题[1-2]。这是由于对预应力损失估计不准确造成的。当预应力损失计算不够精确时,计算得到的混凝土预应力与实际情况产生偏差,结构的实际预应力较低[3-4]。现行《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)和《铁路桥涵混凝土结构设计规范》(TB 10092—2017)中结构的预应力损失的主要因素有6个方面。研究表明,孔道预应力摩阻损失占主要部分[5]。在孔道预应力摩阻损失问题的研究过程中,众多该领域的学者发现通过现场摩阻试验数据拟合得到的摩阻系数比设计值甚至规范推荐值更大[6-7],结构的实际摩阻损失大于规范计算得到的数据。

近年来,学者们在针对规范公式展开了一系列研究,通过改进规范公式的方法来得到更加精确的摩阻损失值。王凌波等[8]利用不同钢束间的变形关系和应力条件,在预应力钢束的实际影响参数与摩阻损失存在显著差异的情况下,推导出更加精确的预应力损失计算公式。张开银等[9]从弹性体接触理论出发,对预应力钢筋与孔道间接触应力进行了探究,通过假设接触应力的3种分布的形式,推导出了弯曲孔道摩阻损失计算公式。黄文雄等[10]根据钢绞线在不同导向半径与弯折角度的条件下弯折摩阻预应力损失情况,并结合现场试验数据,提出了考虑不同导向半径影响的钢绞线弯折摩阻预应力损失计算公式。段江龙[11]对优化了规范中预应力筋伸长值的计算公式,并通过实测数据验证了优化公式。Yu等[12]对接触缺陷对预应力摩阻的影响进行研究,提出一种精度更高的摩阻损失修正方程。

部分学者通过有限元软件以及其他方法来研究预应力摩阻损失。邬晓光等[13]利用MIDAS软件模拟了孔道偏差对桥梁预应力损失的影响,并通过定义广义孔道偏差系数独立了偏差系数,借此提高摩阻损失的计算精度。Shi等[14]基于现有规范中比较复杂的预应力损失计算方法,提出了一种通用的预应力摩阻损失计算模型。郭肖凯等[15]借助ABAQUS比较了不同摩擦系数、弯曲角度、张拉力对计算公式和有限元模拟结果的效应。杨欧峰等[16]通过MIDAS研究了孔道摩擦系数u、孔道偏差系数k对桥梁整体线形和应力产生的影响。李长雨[17]采用软件DR.Bridge,对实际工程进行模拟。由于摩阻系数μ与偏差系数k均与规范存在差异,这导致预应力损失计算的误差,而实际测量出的μ和k值能够很好地体现出当时管道的摩阻状况和偏离程度。罗茂林等[18]通过ANSYS空间模型及现场试验实测了各预应力筋的摩阻损失和对应测点的应力状况,分析了测试截面应力分布情况。Zhang等[19]通过理论分析和实验,指出了现行弯曲孔中有效预应力计算公式的不足之处,并根据对弯曲孔预应力损失摩擦系数影响因素的研究,进一步分析了预应力混凝土结构弯曲孔道预应力损失情况。

综上所述,针对当前规范中孔道预应力摩阻损失计算存在的问题,从摩阻损失原理出发,通过简化规范公式和优化假设条件得出更加精确的摩阻损失计算公式,进而减小实测摩阻损失与理论计算值的差距。通过应用有限元软件,研究不同参数对摩阻损失计算值的影响,并通过实桥摩阻试验进行分析验证。

1 纯弯曲孔道摩阻损失计算

1.1 赫兹接触基本理论

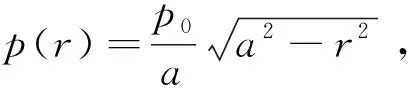
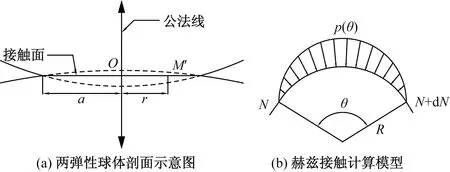
N为张拉力;θ为弯曲角度;R为接触圆半径

1.2 纯弯曲孔道摩阻损失计算公式推导

根据库伦摩擦定律,预应力钢筋与混凝土之间的摩擦力随接触压力的增大而增加,接触压力取决于预应力钢筋所承受的张拉力。摩擦力会使预应力钢筋的张拉力沿接触面减少。由此可以确定这3个因素(摩擦力、接触压力、张拉力)彼此关联并互相影响。假定接触压力是非均匀分布的,接触压力只与弯曲角度θ有关,其分布可表示为p(θ),可得摩擦力为μp(θ),其中μ为摩探系数。张拉力为N,在弯曲孔道全长范围内由摩阻产生的张拉力损失为dN,接触压力的作用下微段上产生的径向力为p(θ)ds,对应的摩擦力为μp(θ)ds。计算示意图如图2所示。

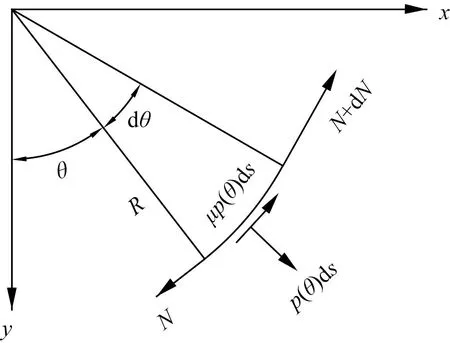
图2 预应力筋微段受力Fig.2 Prestressing tendon micro-segment force

以整体为研究对象,其x轴和y轴上的静力平衡方程可表示为

(1)

(2)

式中:Fxj、Fyj分别为接触压力沿x、y轴上的分力;Fxm、Fym分别为摩擦力沿x、y轴上的分力;Ncon为张拉端的张拉力;Ns为预应力摩阻损失;θ0为弯曲孔道的弯曲角度。

摩擦力和接触压力沿x、y轴上的分力计算方程如下,各分力的方向和其对应坐标轴方向一致时取正值。接触压力沿x、y轴的分力Fxj、Fyj的计算方程为

(3)

(4)

摩擦力沿x、y的分力分别为Fxm、Fym,可分别表示为

(5)

(6)

令α=Fxj,β=Fyj,则可得Fxm=μβ,Fym=-μα。将式(3)～式(6)代入式(1)和式(2)可得

(7)

联立求解方程可得关于α、β的耦合方程为

(8)

(9)

再联立式(8)和式(9)可得

(10)

当接触压力为非均匀分布时,与张拉控制力相比,α对预应力摩阻损失的影响较小。因此忽略α及其系数对摩阻损失计算值的效应,从而得出非均匀压力下纯弯曲孔道计算公式为

(11)

2 有限元分析

2.1 有限元模型建立

为了研究不同摩阻损失参数对弯曲孔道预应力摩阻损失的影响,应用有限元软件ABAQUS模拟纯弯曲孔道中预应力钢筋与混凝土的接触行为。本模型是基于面的接触,主控表面为混凝土表面,从属表面为预应力筋表面,接触面约束施加算法为罚方法,罚刚度比例系数为1。接触跟踪方式为有限滑移。混凝土及预应力筋两者均采用C3D8R实体单元,采用扫掠的网格划分方法。混凝土的网格尺寸为50 mm,预应力筋的网格尺寸为10 mm。网格在接触的核心区域被进一步细化。混凝土强度等级为C50,预应力筋弹性模量取1.95×105MPa,泊松比为0.3,抗拉强度标准值fpk=1 860 MPa 。根据工程的实际状况,弯曲孔道的半径R′设定为6 m,混凝土截面尺寸设定为1.0 m×1.0 m。预应力筋的等效半径re为30 mm,如图3所示。有限元模型如图4所示。

图3 模型参数Fig.3 Model parameters

图4 摩阻损失分析模型Fig.4 Frictional loss analysis model

2.2 摩阻损失分析

为了验证推导公式的适用性,现从不同摩阻损失参数出发,通过对比规范公式和推导公式的理论解和有限元的数值解Nb进行分析张拉控制应力、弯曲角度、摩擦系数对摩阻损失计算值的影响。根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018),纯弯曲摩阻损失可表示为

N1=Ncon(1-e-μθ)

(12)

2.2.1 张拉控制应力对摩阻损失计算值的影响

选取200、500、800、1 000 MPa的张拉控制应力,在摩擦系数μ=0.2、弯曲角度θ为30°和60°的条件下,分别计算预应力摩阻损失值及其偏差。具体分析数据如图5所示。

σcon为张拉控制应力

由图5可知,弯曲角度θ、摩擦系数μ一定时,摩阻损失系数为定值,与张拉控制应力无关。当弯曲角度为30°时,随着张拉控制应力的增加,摩阻损失系数为0.144;当弯曲角度为60°时,摩阻损失系数为0.240。在不同工况下,推导公式计算的摩阻损失值与有限元数值解的差值较小,且随着张拉控制应力的增大,公式的理论解与有限元的数值解的差值随之增大。

2.2.2 弯曲角度对摩阻损失计算值的影响

选取30°、60°、90°、120°、150°的弯曲角度,在摩擦系数μ=0.2、张拉控制应力σcon=1 000 MPa的条件下,分别计算预应力摩阻损失值及其偏差,具体分析数据如图6和图7所示。

图6 不同弯曲角度下摩阻损失Fig.6 Friction loss under different bending

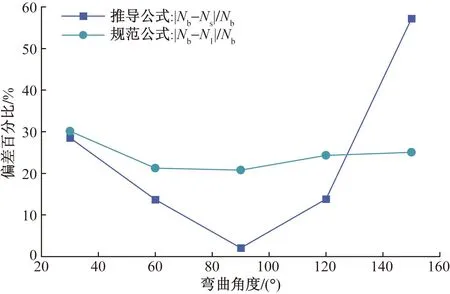
图7 偏差Fig.7 Deviation

由图7可知,当角度在30°～120°时推导公式理论解和有限元的数值解的偏差比规范公式计算的摩阻损失偏差小。当弯曲角度为30°时,推导公式的偏差比规范公式的偏差低2%。当弯曲角度大于60°小于120°时,推导公式计算理论解与有限元数值解偏差保持在15%以内,规范公式在20%以上。当最大弯曲角度小于120°时,采用推导公式计算的预应力弯曲孔道摩阻损失比规范公式更精确。

2.2.3 摩擦系数对摩阻损失计算值的影响

选取摩擦系数为0.1、0.2、0.3、0.4、0.5,在张拉控制应力σcon=1 000 MPa、弯曲角度θ为30°、90°的条件下,分别计算预应力摩阻损失值及其偏差,具体分析数据如图8和图9所示。

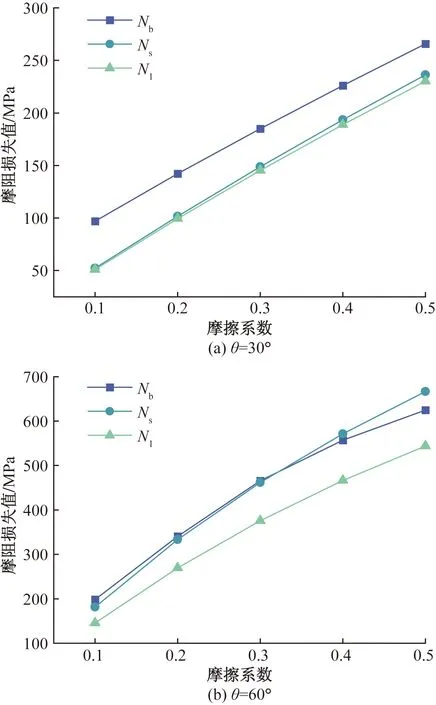
图8 不同摩擦系数下摩阻损失Fig.8 Friction loss at different friction coefficients

图9 偏差Fig.9 Deviation

由图9可知,弯曲角度为30°时,推导公式的计算值与规范公式计算值的差值较小,且两者与有限元计算结果的偏差值随摩擦系数的增大而减小,当摩擦系数为0.1时,偏差值均在45%以上,当摩擦系数为0.5时,偏差值均在约10%。当弯曲角度为60°时,在给定的摩擦系数下,推导公式的计算值更接近有限元分析的结果。推导公式与有限元的偏差值随摩擦系数增大先减小再增大,摩擦系数为0.3时偏差最小,在摩擦系数为0.2～0.4范围内,偏差保持在3%以内。

3 孔道预应力摩阻损失实验研究

3.1 工程概况

选取福州至长乐机场城际铁路工程线路上60 m+100 m+60 m连续刚构桥作为研究对象,采用应变分布法进行摩阻试验,利用应变传感器测得预应力筋在分级张拉力作用下的摩阻损失数据。预应力筋采用φs15.2高强度低松弛预应力钢绞线,弹性模量为1.95×105MPa,抗拉强度标准值为1 860 MPa,锚下张拉控制应力为1 395 MPa。预应力管道采用金属波纹管成孔,预应力筋选取F1束和F4束(型号均为15-φs15.2),管道摩擦系数设计值取0.23,偏差系数设计值取0.002 5。主梁截面尺寸如图10所示。预应力筋线形如图11所示。

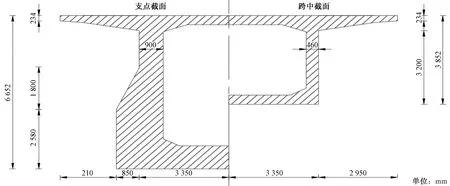
图10 主梁截面尺寸Fig.10 Main beam section size

F1、F4为预应力钢束名称

3.2 测试流程

在待测预应力束中各选取一根预应力钢绞线为研究对象,预应力束示意图如图12所示,几何参数如表1所示。

表1 预应力束几何参数Table 1 Geometric parameters of prestressing beam

L1～L2为钢束直线段、曲线段长度; x1～x4为钢束竖直投影长度

每束钢绞线两端预留1.2 m工作长度以便安装仪器。定位各应变测点并标记。将待测试钢绞线固定于预应力束的最上端,并沿其外缘粘贴电阻应变片,测点位置如图13所示。1#、7#测点位于钢绞线计算长度两端,4#测点位于主墩中心线处,其余测点均位于曲线段端点上。在每个应变片在安装完后,使用万用表对其进行测量检测,以确保每个应变片均能正常运行。

1#～7#为测点

全部钢绞线绑扎完毕后利用卷扬机进行穿束,直至预应力束到位,引出将连接电阻应变片的导线,依次安装穿心式压力传感器、限位板、千斤顶、工具锚及夹片。将电阻应变片的导线连接入静态应变仪后,准备加载。设备安装如图14所示。

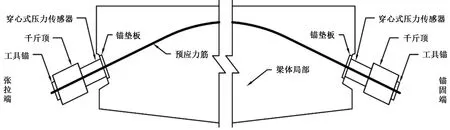
图14 孔道摩阻损失测试设备安装示意图Fig.14 Schematic diagram of orifice friction test installation equipment

本次试验采用单端张拉的方式进行加载。张拉端完成预加载后(预加载荷载为0.1σcon),将静态应变仪示数归零。然后张拉端开始分级匀速张拉,张拉力为0.3σcon、0.6σcon、1.0σcon,分别记录不同张拉力下压力传感器及静态应变仪的读数。

3.3 试验结果分析

孔道偏差摩擦损失计算值分别采用《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)公式(以下简称规范公式)及本文推导公式进行计算,所推导的总弯曲孔道预应力摩阻损失表达式为

(13)

规范公式为

σs=σcon[1-e-(μθ+kx)]

(14)

式中:σd为推导公式计算的总摩阻损失值,MPa;σs为规范公式计算的总摩阻损失值,MPa;k为管道每米局部偏差对摩擦的影响系数。

利用静态应变仪记录钢绞线在张拉阶段的应变数据,获得各张拉工况下预应力钢绞线的实测应变值,如图15所示。

图15 各测点实测应变值Fig.15 Measured strain value at each measurement point

由图15可知,直线段上的测点由于仅受孔道偏差的影响,其变化较为平缓。在曲线上的3#、6#测点同时受到弯曲摩擦损失和偏差摩擦损失的作用,因此实测应变下降幅度较显著。可以看出,F1和F4的应变均随测点编号的增加不断减小,说明摩阻损失在不断累积。

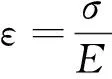
图16 实测应变与理论应变Fig.16 Measured strain and theoretical strain

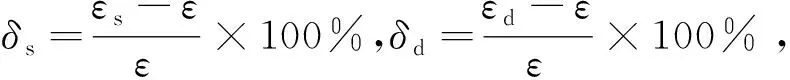
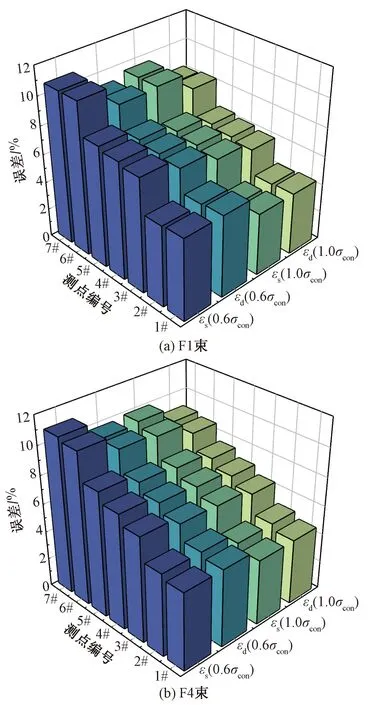
图17 误差对比Fig.17 Error comparison

由图17可知,在相同张拉工况下,任意测点处δs均小于δd,说明本文推导公式相比规范公式更能精确地预测摩阻损失。与规范公式相比,弯曲角度越大、张拉应力越大,推导公式的计算结果越接近实际情况。

4 结论

基于赫兹接触理论,推导了在任意非均布力下考虑摩擦力、接触压力、张拉力之间耦合作用的纯弯曲孔道摩阻损失公式。通过有限元软件ABAQUS模拟纯弯曲孔道预应力钢筋和混凝土之间的接触行为,并对不同因素对摩阻损失计算值的影响进行深入探讨。通过预应力连续刚构桥实桥摩阻试验,对比推导公式和规范公式计算得出应力计算值与实测数据的误差,得出以下结论。

(1)当弯曲角度小于120°时,通过推导公式计算出的结果更接近有限元数值解。当弯曲角度大于120°时,由于忽略参数α值及其系数的影响使得计算结果会产生较大误差,因此得到推导公式的适用于最大弯曲角度不超过120°的单段圆弧。在摩擦系数在0.2～0.4范围内时,推导公式与有限元计算的结果高度一致。满足实际桥梁对摩擦系数取值范围的要求。

(2)经过弯曲孔道摩阻试验的研究表明,当预应力孔道弯曲角度较小时,推导公式与规范公式的摩阻损失计算结果基本一致;但随着张拉应力和弯曲角度的增加,推导公式与规范公式得到的摩阻损失计算值差值逐渐增大。当弯曲角度较大时,推导公式的计算值将显著大于规范公式,且更接近实测值。因此,通过推导公式计算预应力连续刚构桥的腹板束的摩阻损失,可以在一定程度上减少对预应力损失的误判,从而为确保桥梁结构具有有效的预应力提供重要的支持。