张拉整体结构的智能化找形研究进展

郭茂祖, 李卓璇, 李阳, 邵首飞

(1.北京建筑大学电气与信息工程学院, 北京 100044; 2.建筑大数据智能处理方法研究北京市重点实验室(北京建筑大学), 北京 100044)

美国著名建筑师R. Buckminster Fuller比喻宇宙中的天体像是漂浮在万有引力的拉力海洋之中的、受压的孤岛,大自然中有“间断压、连续拉”的现象[1]。他的学生Kenneth Snelson受到启发,设计了一件名为“Snelson’s X”的艺术作品。之后,Fuller[2]通过结合“tensional”(张拉)和“integrity”(整体)创造了“tensegrity”(张拉整体)这一新名词并申请专利。张拉整体结构被定义为由一组不连续的受压构件和连续的受拉单元组成的自支承、自应力空间结构,无需外部的支撑与锚固等固定装置,即可通过自应力保持自平衡稳定状态。且在平衡状态时,压杆都处于压缩状态,拉索都处于拉伸状态,因此,当受到临时扰动时,结构有返回其平衡配置的趋势[3]。

2016年,AlphaGo击败了国际象棋世界冠军,这一事件立即引起全球对人工智能的兴趣[4]。人工智能(artificial intelligence,AI)定义为“一个系统能够正确解释外部数据,从这些数据中学习,并利用这些学习通过灵活的适应来实现特定目标和任务”[5]。人工智能是通过训练计算机来学习和模拟人类的某些思维过程和行为,如学习、推理、判断和决策等。AI已经在语音识别、图像处理、专家系统、自动定理证明和自动驾驶汽车等应用领域取得了显著成果[6]。机器学习是实现人工智能的一种方式,它描述了系统从特定问题的训练数据中学习,以自动化分析模型的构建过程并解决相关任务的能力,不是将知识编码到计算机中,而是寻求从示例和观察中自动学习有意义的关系和模式[7]。深度学习是机器学习领域中新的研究方向,是基于人工神经网络的机器学习概念,它被引入机器学习使其更接近于最初的目标——人工智能[8]。

因此,有学者将人工智能技术引入建筑领域中,如建筑能耗预测[9]、智慧城市建设[10]和建筑消防安全[11]等。AI在建筑设计中的应用主要包括:基于案例的建筑设计、建筑风格学习的模式识别和建筑环境系统设计等[12-13]。2017年 5月,“世界上第一个人工智能建筑师”小库xkool应用机器学习、大数据与云端智能显示技术构建了人工智能建筑设计SaaS系统,标志着人工智能进入建筑设计行业的时代已经到来[14]。

现主要针对使用人工智能技术改进张拉整体结构的找形方法展开相应的讨论。首先介绍何为张拉整体结构以及人工智能技术在建筑领域的应用;其次论述研究张拉整体结构智能找形方法的意义,介绍各个传统张拉整体结构找形方法及其优缺点,分析智能找形中外相应研究现状并对智能找形方法展开详细的分析;最后给出结论,对未来的研究趋势提出相应的见解,对相关研究人员开展下一步研究工作具有一定的参考意义。

1 张拉整体结构智能找形方法研究意义

张拉整体结构可大致分为两类[15]:第一类是受压构件之间相互不连接,即多个受压构件不会共用一个节点;第二类是受压构件之间会相互连接,即两个及以上的受压构件由同一节点连接。由于第二类结构受力复杂导致建模难度较高,因此目前大多数的找形研究是针对第一类张拉整体结构。张拉整体结构体系自20世纪50年代诞生以来,受到结构工程界,尤其是建筑结构工程界的广泛关注,被建筑师和结构工程师认为是未来的结构体系。受其启发,索穹顶、弦支穹顶、索桁结构、张弦结构等新型的预应力、自平衡结构体系不断涌现,成为大跨度空间结构创新的主要源泉之一。由于张拉整体结构外形美观、质量轻、强度大、易建模、材料利用率高、形态可调、不需要复杂的接头等特点,近些年来,张拉整体结构越来越受到其他学科领域的关注,基于张拉整体结构建筑学[16]、机器人学[17]、生物医学[18]、航空航天[19]等方面的研究方兴未艾。目前,由张拉整体结构建成的经典建筑物包括韩国奥运会体操馆、美国圣彼得堡的雷声穹顶、德国科隆比赛馆、荷兰赫伦文溜冰场、中国北京世界园艺博览会比利时馆等[20]。

结构的形状确定问题就是确定平衡状态的问题,被称为“找形”。“找形”是设计张拉整体结构的关键步骤之一,即找到结构自应力状态下的平衡构型,需要同时实现两个目标:几何形状和自应力[21]。张拉整体结构常用的传统找形方法可分为几何分析法、静力学方法和运动学方法。几何分析法主要用于研究正多面体[22]的张拉整体结构,局限性较大。静力学方法又可细分为解析解法、力密度法(force density method,FDM)和能量法。解析解法主要将对称的多面体作为研究对象,比如棱柱形张拉整体和截断形正多面体[23]。力密度法使得找形问题线性化,但力密度值的选取需要经验,当结构复杂或不规则时,选取很困难[24]。运动学方法又可细分为解析解法、非线性规划法、动力松弛法和坐标缩减法[25]。在非线性规划法中,约束方程的数目会随着节点数增大而增大,导致计算量增加。动力松弛法相对于节点数较少的结构收敛较快,但当节点数增加时,收敛明显变慢[26]。坐标缩减法虽然对结构的形状控制效果不错,但其计算量过大[27]。

从“中国建造”走向“中国智造”是中国建筑业发展的大势所趋。由于张拉整体结构传统的找形方法存在着计算过程复杂、计算步骤烦琐等问题,因此需要进行智能化的改进,引入人工智能的一些方法,如元启发式算法、神经网络等。传统找形方法虽然计算准确,但所需迭代次数多,计算复杂度高。引入元启发式算法后可将找形问题转化为约束优化问题[28],简化找形流程并提高效率,算法总能根据目标函数和约束找到解[29],但是解并不唯一。传统找形方法与人工智能技术相结合,形成张拉整体结构的智能找形方法。

2 张拉整体结构传统找形方法

张拉整体结构传统的找形方法可分为几何分析法、静力学方法和运动学方法。其中,静力学方法又可细分为解析解法、力密度法和能量法。动力学方法又可细分为解析解法、非线性规划法、动力松弛法和坐标缩减法。

2.1 几何分析法

几何分析法是利用几何的对称性进行分析找形,主要用于研究正多面体的张拉整体结构,局限性较大。

2.2 静力学方法

静力学方法是在具有给定拓扑结构的平衡配置与其构件中的力之间建立了关系,然后用各种方法分析这种关系[30]。静力学方法又可分为解析解法、力密度法和能量法。

(1)解析解法主要将对称的多面体作为研究对象,研究范围不够广泛。

(2)力密度法[31-33]通过指定索和杆的力密度(力密度指构件的内力和构件的长度的比值),建立节点的平衡方程,求解得到节点坐标,从而确定平衡结构。力密度法通过使用简单的数学技巧将节点的非线性平衡方程转换为一组线性方程,将找形问题线性化,可以凭借较少的初始信息找到张拉结构的自平衡状态。但力密度值的选取需要经验,当结构复杂或不规则时,选取很困难,而且不适合寻找张拉结构的配置细节。具体力密度法算法描述如算法1所示。

(3)能量法最早由Connelly等[34]提出,其灵感来源于力密度法,且原理和力密度法大致相同,他通过提出一个能量函数将能量和刚度之间的关系公式化。

力密度法的具体算法流程如下。

算法1 力密度法 输入:初始力密度Q、构件类型、拓扑结构。输出:更新后的力密度。1.根据拓扑结构和构件类型构建连接矩阵C;2.构建力密度矩阵D=CTQC;3.对力密度矩阵进行特征值分解D=ΦΛΦΤ(Λ为D对应的特征值组成的对角矩阵,Φ为对应的特征向量组成的矩阵),求解得到节点坐标;4.构建平衡矩阵A=CTdiag(Cx)CTdiag(Cy)CTdiag(Cz) ;5.对平衡矩阵进行奇异值分解A=UVWT,更新力密度值(V为A的非负奇异值组成的对角矩阵,W为ATA的特征向量组成的矩阵);6.判断是否满足平衡条件,若满足,则输出更新的力密度值;若不满足,则返回到第2步,重新计算力密度矩阵;7.结束。

2.3 动力学方法

动力学方法是保持索的长度和比例不变,支柱长度增加,直到达到最大值;或者保持支柱长度不变并固定比例,缩小索的长度,直到达到最小值。运动学方法又可分为解析解法、非线性规划法、动力松弛法和坐标缩减法。

(1)解析解法适用于对称结构,对于非对称情况,由于描述一般构型需要大量变量,此方法变得不可行。

(2)Pellegrino[35]提出的非线性规划法将任何张拉整体结构的找形转化为约束最小化问题。从已知元件连接性和节点坐标的系统开始,一个或多个支柱被拉长,保持固定的长度比,直到达到其长度最大化的配置。在非线性规划法中,约束方程的数目会随着节点数增加而增大,导致计算量增加,因此这种方法对于更大的结构是不可行的。

(3)Motro[36]和Belkacem[37]提出了已成功用于膜和索网结构的动力松弛方法。作为张拉整体结构的通用找形方法,动力松弛法由迭代的两个步骤组成。第一步计算每个节点上的总力,称为残余力,如果结构处于完美平衡,这些力将为零。第二步调整每个顶点的位置,以减少作用在其上的残余力。重复这两个步骤,直到最大残余力低于期望阈值,方法的具体流程如算法2所示。相对于节点数较少的结构收敛较快,且可以从任意假设的不平衡状态开始迭代直到得到平衡状态,但当节点数增加时,收敛明显变慢。

(4)坐标缩减法是一种根据虚功原理推导平衡方程的方法,虽然比起力密度法可以更好地控制形状,但其具有大量的符号处理步骤,这不利于实现计算机编程工作。

动力松弛法的算法描述如下。

算法2 动力松弛法 输入:拓扑结构、构件原长。输出:节点坐标。1.建立初始几何模型;2.计算每个节点上由外力和内力组合产生的不平衡力;3.计算节点的最大刚度以及虚拟质量;4.计算节点的加速度和速度;5.计算更新后的节点坐标;6.由新的节点坐标计算节点不平衡力,并判断是否满足精度,若满足,则退出迭代,继续第7步;若不满足,则将所有节点速度重置为0,返回第2步重新迭代计算;7.计算体系总动能,判断动能峰值;8.结束。

3 张拉整体结构智能找形方法研究现状

自20世纪初,张拉整体结构被发明以来,找形的问题就受到了广泛的关注。近年来,学者们对张拉整体结构(Tensegrity)及其找形(Form-finding)的研究越来越多,图1展示了在 Web of Science 网站上分别搜索关键词“Tensegrity”“Tensegrity”“Form-finding”得到的论文数量。近年来,一些学者已经开始将传统找形方法和人工智能技术相结合,以克服传统方法存在的一些局限性和不足之处。

图1 Web of Science上“张拉整体结构”和 “张拉整体结构找形”文章数量Fig.1 The number of articles about “tensegrity” and “tensegrity+form-finding” on Web of Science

目前,已存在的使用人工智能方法对张拉整体结构的找形进行智能化改进的方法可分为两类:第一类是将传统的找形方法和一些优化算法相结合,将找形问题转换成约束优化问题进行求解;第二类是在结合优化算法的基础上,再引入神经网络技术优化找形方法。

3.1 结合优化算法的智能找形方法

第一类方法将传统的找形方法与优化算法相结合,通过最大化或最小化目标函数并设置适当的约束条件,将复杂的找形问题转化为约束优化问题。其基本流程为:①定义优化目标函数,可以是最小化构件材料成本、最小化结构体积、最小化结构变形等;②设定约束条件,包括构件受力约束、位移限制、变形限制等。选择合适的优化算法,如元启发式算法和数学规划法等,对目标函数进行优化;③循环迭代,直到满足约束条件和目标函数的要求;④最后输出最优的结构形态和参数,作为最终的结果。通过这种方法,可以在保证结构稳定性和约束条件的前提下,实现结构参数的最优化设计,提高结构的经济性和可靠性。

如表1[38-56]所示,使用力密度法的研究人员明显多于动力松弛法,这是由于在研究不对称结构或具有较多节点的结构时,动力松弛法计算量过大。调研显示,遗传算法似乎更受青睐,但近几年,研究者更倾向于使用其他优化算法以规避遗传算法的缺陷。优化算法是一种在不违反约束条件的情况下,根据概率通过最大化或最小化目标函数对问题寻找最优解的过程,但无法保证一定能得到最优解,对于相同的输入可能会得到不同的输出结果。元启发式算法是相对于最优化算法提出来的,大自然对于开发元启发式算法提供了重要的灵感[57]。元启发式优化算法是一种解决全局优化问题常用的方法,它主要是通过模拟自然和人类智慧来实现最优解的求解。常见的元启发式算法有遗传算法、蚁群优化算法、粒子群优化算法、人工鱼群算法、人工神经网络等等。

表1 结合优化算法的智能找形方法总结[38-56]

遗传算法是一种典型的启发式算法,它在解决复杂问题、优化搜索空间大且多参数的情况下具有较好的适应性和鲁棒性,一些学者通过引入遗传算法来实现张拉整体结构的形态优化。Paul等[38]将动态松弛法和遗传算法相结合,将顶点的初始位置和结构的连接模式直接编码到基因中,通过遗传算法来优化结构的连接模式和参数值,然后使用动态松弛法来动态调整构件长度并确定最终平衡形状。结果表明,优化算法可以成功探索不规则结构的空间,并产生新的未知构型,可以作为张拉整体结构自由设计的工具,但该方法存在一定的缺陷,即进化的前几代基因生成的大多是一维或二维的结构,效率不高。针对这个问题,许贤等[39]提出对非三维结构赋予非零罚函数,使得它们的适应度函数小于三维结构。为解决自由形态的非规则张拉整体结构的找形问题,许贤等在动态松弛法的基础上引入并行的遗传算法,通过优化节点的空间坐标和索的刚度来找到平衡构型,与文献[38]使用的遗传算法不同的地方在于,此文提出的遗传算法使用更简单的二进制编码代替实数编码,并引入小生境技术以确保个体的多样性,并通过选择合适的罚函数来平衡优良基因的保留和算法的收敛速度。此方法除了存在动态松弛法对大量节点无效的缺点外,还存在着对结构特征无特殊约束的限制,只能优化某些全局目标,如体积和跨度。 Dasari 等[41]结合遗传算法和动态松弛法对废物收集中心的屋顶结构进行了设计与优化,虽然高效且直观,但其仍未摆脱对建模软件的依赖。

Yamamoto等[44]提出了结合力密度法和遗传算法的张拉整体结构数值找形方法,通过将连接矩阵和原始力密度编码到两个不同的染色体中形成具有不同遗传信息的种群,且使用3个适应度函数的和来评估个体适应度,分别对自应力状态数、节点处构件最少数量和压杆之间不能相互连接三个条件进行了约束,此方法仅需要较少的信息就可寻找张拉整体结构的自应力状态。Koohestani[45]也通过使用基于遗传算法的力密度法对张拉整体结构进行找形,已知构件的类型及拓扑结构,通过最小化与力密度值和最小特征值相关的目标函数来优化力密度,进行找形。并且还提出了两种方法将非对称结构转化为对称结构。对于节点固定的几何结构,压杆和拉索的不同连接模式可能会产生一些新颖的张拉整体结构。对于遗传算法,虽然第一代初始配置相同,但不会收敛于唯一的自平衡配置,而是会找到理论上正确的不同配置。Lee等[48]结合遗传算法,对于具有多自应力状态的结构,使用不同的约束条件,获得单一的稳定结构。

遗传算法在离散域中随机选择最优解,并基于步长定义搜索空间,因此它在寻找合适候选解的收敛过程中存在缺陷。为了避免遗传算法带来的局限性,Chen等[58]提出离散的优化模型,将找形问题转换成修改后的旅行商问题,将固定的节点视为网络中的城市,设置与稳定性和刚度相关的目标函数,将节点的连接情况视为唯一变量,通过蚁群算法搜索可行的解决方案。与结合遗传算法的大部分方法相比,此方法具有更强的全局搜索能力和较快的搜索速度。林敏等[51]提出了将力密度法与改进的鱼群算法相结合的张拉整体结构找形方法,提出合适的目标函数和约束条件,将找形问题转换成如何搜索符合条件的最优力密度的问题,避免了大量的矩阵分解运算,且提高了算法的精度和效率。Do等[53]通过对差分进化算法进行改进并将其与力密度法相结合,实现了对张拉整体结构的优化,充分利用差分进化算法的全局搜索能力。粒子群算法也是典型的元启发式算法,具有收敛快、参数少等特点,已被应用在结构设计领域[59-60]。伍艺等[54]提出将力密度法与粒子群算法相结合,将找形问题转换成使用粒子群算法根据目标函数,寻找最优力密度的问题,以解决传统力密度法效率低的问题。除粒子群算法外,Chen等[55]还结合对称性分析对张拉整体的自平衡形态进行研究与分析。

除了启发式算法,还存在部分融合了数学规划法的张拉整体结构形态智能设计方法。数学规划法是一类用于求解优化问题的数学方法,它通过建立数学模型,将问题转化为一个或多个数学表达式,并通过数学分析和计算来寻找最优解或满足一定条件的解。Cai等[52]提出了一种既适合于规则结构又适合于不规则结构的数值找形方法,将力密度法与梯度下降法组合,通过对平衡条件的一些约束,将找形问题转换为最小化问题,找出符合条件的力密度,并分别举例说明此方法的可行性和正确性。张拉整体平衡结构如图2所示。张沛等[42]在梯度法的基础上引入动力松弛技术,改善了梯度法寻优精度不高、后期收敛变慢等问题。但由于梯度下降方法容易陷入局部最优,部分学者提出使用其他算法。Arcaro等[43]对于超弹性张拉整体结构,使用拟牛顿法基于最小总势能原理寻找结构的平衡状态。Wang等[56]通过序列二次规划法将力密度的确定转化为秩的最小化问题,此方法同时适用于具有单个或多个平衡状态的张拉整体结构。启发式算法具有处理复杂非线性问题和接近最优解的优点,但全局最优解和结果的稳定性无法得到保证;数学规划法则具备较强的理论基础和数学支持,能够精确寻找最优解,但可解决的问题类型有较大的局限性,可能会受到维度灾难和初始解依赖性的影响。

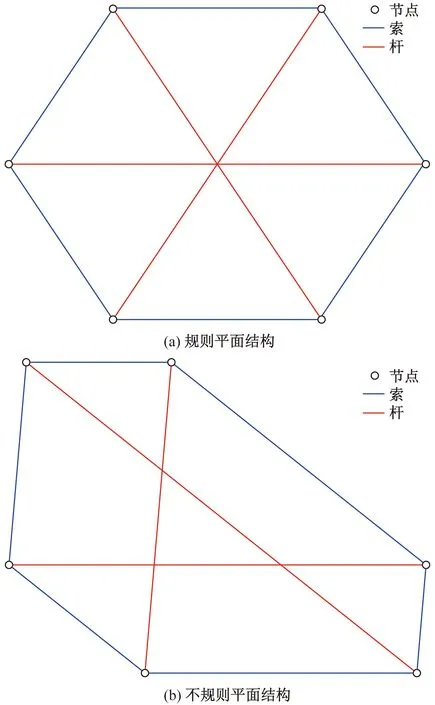
蓝色线为拉索;红色线为压杆;圆圈为节点

以往大多数找形方法需要给定拓扑结构和构件类型。Lee等[46]提出将力密度法与遗传算法相结合的找形方法,与以往方法不同的是,该方法仅需节点的连接情况作 为初始数据,根据杆的不连续条件(一个节点仅能连接一根杆的条件)就可以确定杆的候选集,确定构件类型后,再通过遗传算法优化步骤,搜索出合适的力密度,构成平衡形状。Gan等[47]提出了一种新的数值找形方法,仅需节点数量就可完成张拉整体结构的找形,根据两根支杆不能连接同一节点这一条件,设置杆的数量为节点数量的1/2。通过确保无相同连接性成员对连接矩阵进行猜测,再对力密度进行初始赋值,然后将连接矩阵和初始的力密度值编码到两个不同的染色体中,进行优化操作以找到平衡构型,但该方法缺少实例证明。Lee等[50]结合双循环遗传算法和力密度法,在构件类型未知,只需节点连接性的情况下,找到截断四面体的平衡形状。Lee等[49]开发了一种使用相应力密度参数绘制平衡状态的找形方法,然后使用遗传算法产生一个的可行力密度集,并发明一种新的销连接方式。为找到期望的几何配置, Bui等[40]通过使用遗传算法满足结构高度、底面宽度等约束条件,并使用动力松弛法获得最终参数,克服了动力松弛法不能满足几何约束和对初始形状过于敏感的缺陷。

3.2 结合神经网络的智能找形方法

第二类智能找形方法是在结合优化算法的基础上,引入神经网络进行优化或预测,这种方法是目前较先进的张拉整体结构找形方法。这类方法可分为:第一类是结合优化算法与传统找形方法以生成张拉整体结构的数据集,再训练神经网络预测相关参数,以构建平衡构型;第二类是结合优化算法将找形问题转化为约束优化问题,再运用神经网络求解此问题。神经网络模型的灵感来自于动物的中枢神经系统,通常呈现为相互连接的“神经元”,它通过调整内部大量节点之间相互连接的关系,从而达到处理信息的目的,是一种进行分布式并行信息处理的算法数学模型。

周轶凡等[61]使用Grasshopper平台下的遗传算法Octopus插件,对壳体模型的最大形变、整体的重量以及应变能3个目标函数进行优化,生成2 039组四维数组,并将其输入搭建好的全连接的人工神经网络,进行回归计算,从而实现更大样本数量的预测和优化,提高优化效率。但是此方法不是针对张拉整体结构设计的。Lee等[62]提出了适用于张拉整体结构的智能找形方法,大致思路与周轶凡等[61]相近,方法流程如图3[62]所示,此研究使用改进后的差分进化算法(differential evolution DE),通过最小化目标函数来生成满足要求的力密度集,再将所得到的50 000条力密度输入到搭建好的深度神经网络(deep neural networks,DNN)中进行训练和测试,预测结构中各个构件的长度,进行找形,共给出3个张拉整体结构的数值案例进行验证,均取得不错的结果。此方法可以省去传统力密度法中的特征值分解和奇异值分解过程,简化了找形流程。对于截面四面体,差分进化算法与深度神经网络的误差对比如图4[62]所示。但仍存在一些问题有待改良,如一种网络结构只适用于一种张拉整体结构,因此对于不同的结构需要重新训练神经网络。 Trinh 等[63]提出了一种通过训练各构件中点坐标来预测构件力密度的方法。然而,此方法需要针对不同的构件训练不同的网络,操作烦琐。这是已有的张拉整体神经网络智能找形方法存在的共性问题,一个神经网络结构仅能训练和预测一个构件或结构,不具有广泛适用性和通用性。

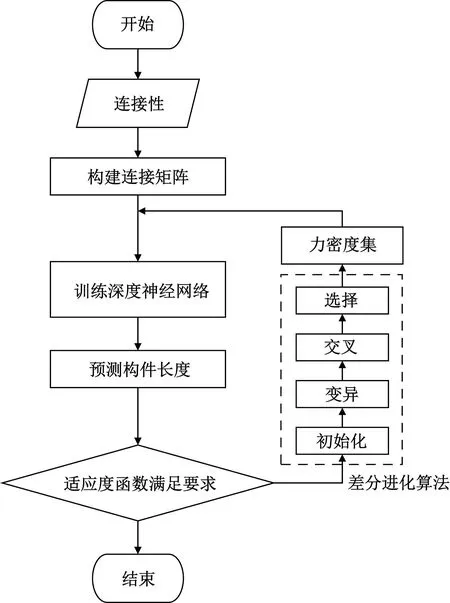
图3 力密度法与深度神经网络相结合的找形流程图[62]Fig.3 Flow chart of combining force density method with DNN for form-finding[62]

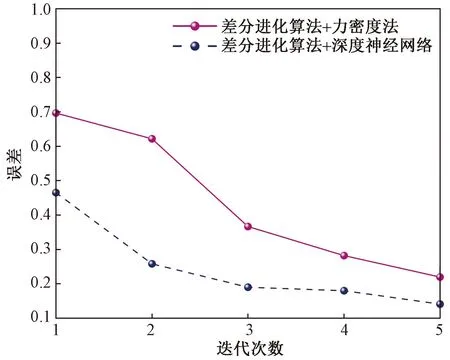
图4 差分进化算法分别与力密度法和深度神经网络 结合时误差对比图[62]Fig.4 Error comparison diagram when DE is combined with FDM and DNN respectively[62]

还有部分学者通过提出新的神经网络,并将其与传统找形方法相结合,以此来解决张拉整体结构的找形问题。Sun等[64]提出一种基于力密度法和归零神经网络的张拉整体结构找形方法,首先使用最小二乘法将找形问题转化为非线性无约束优化问题,再使用改进的拟牛顿法近似替代Hessian矩阵,这样可以保证矩阵的正定性以确保张拉整体结构的稳定性,但同时也引入了误差,最后使用抗噪的归零神经网络对节点坐标进行迭代运算,求解出符合要求的坐标。此方法既保证了张拉整体结构的稳定性,又可以抑制找形过程中的噪声。但是对于大规模的复杂结构,该算法不能有效地进行找形操作。Sun等[65]基于相同的思路,再次进行了实验,并将最小二乘法替换成了拉格朗日乘子法,此方法的局限是仅适用于对称的张拉整体结构。Zhao等[66]基于Sun等[64]的思路提出了基于抗噪归零神经网络的动力松弛法,使用动态松弛法和序列规划法替代力密度法和最小二乘法。首先将找形问题转化成以节点坐标为变量的非线性约束优化问题,并结合序列规划法与归零神经网络解决此问题,其中,也使用拟牛顿法计算近似矩阵代替Hessian矩阵以减少计算的复杂性。此模型结构简单且计算效率高,同时具有良好的抗噪声性能。

4 结论与展望

张拉整体结构无需外力,可通过自应力保持平衡稳定,且具有外形美观、质量轻、强度大等优势及特点,受到了广泛关注。“找形”作为张拉整体结构设计的关键步骤,主要在于确定平衡状态。针对张拉整体结构的找形方法进行综述,以理清找形方法的发展历程,研究瓶颈以及随着人工智能的发展,找形方法的新转变和特点,并展望未来可能的研究方向及相应的发展趋势。

对于传统找形方法,按照几何分析法、静力学方法和动力学方法来进行分类阐述,虽具有计算准确度高的优点,但存在步骤烦琐、计算复杂等问题。随着人工智能的发展,其具备从示例和观察中自动学习隐藏关系和模式等优势,因而,引入人工智能研究张拉整体结构的智能找形方法受到广泛关注,有望改进传统找形方法,简化找形流程。对于智能找形方法,根据所应用的技术不同,将其分为:第一类是结合优化算法的智能找形方法,通过引入优化算法将找形问题转化为求解目标函数的约束优化问题;第二类是结合神经网络的智能找形方法,通过引入神经网络对结构进行优化或预测。在总结当前已有的研究成果时,发现研究人员所使用的优化算法和神经网络在不断更新。在总结上述研究的基础上,预测并分析总结该领域未来可能的研究方向及相应的发展趋势如下。

(1)目前大多数基于优化的找形方法仅对单个目标进行优化,或直接将多个目标线性组合,而忽略了权重问题。未来趋势是研究多目标和多约束条件的优化算法,以协调各种设计目标和约束条件之间的潜在冲突。

(2)随着人工智能方法的不断发展,引入最先进的理论及算法有望解决更复杂的问题,如利用最新的深度学习技术对大量结构数据进行学习和分析,以实现更准确、高效的张拉整体结构智能找形,有望进一步提高对结构特性的理解。

(3)形状设计的考虑范围应扩展到形状之外的多个方面,包括但不限于材料的选择、结构的重量、工程成本等实际因素。这种综合性的设计方法旨在创造更具实际应用价值的解决方案。

(4)除形状设计外,可将人工智能方法引入张拉整体结构的拓扑设计和预应力设计中,提高设计效率,减少试错成本。为未来的智能结构设计和建设提供更多的可能性。